Modeling and Simulation
Vol.07 No.03(2018), Article ID:26649,9
pages
10.12677/MOS.2018.73021
Modeling of Path Choice via Public Transit Based on the Random Theory
Jiaxian Liang1*, Jiandong Qiu1, Jiajie Pan2
1Shenzhen Urban Transport Planning Center Co., Ltd., Shenzhen
2Traffic Information Engineering & Technology Research Center of Guangdong Province, Shenzhen

Received: Aug. 10th, 2018; accepted: Aug. 22nd, 2018; published: Aug. 29th, 2018

ABSTRACT
The paper presents the analysis of the stop choice and bus choice behaviors in space-time dimension using the public transit path choice model under the framework of random utility models, based on the idea of hierarchical information processing. The parameters of the perceived utility function of bus choice are calibrated and tested from TIYUZHONGXIN BRT stop to DONGPUZHEN BRT stop (8 direct routes) in Guangzhou with IC data and bus arriving data in case study. The result shows that waiting time, on-board time, comfortable at stop, comfortable at bus and the on-board experience are statistically significant in bus choice model under the hierarchical processing of degree of comfort.
Keywords:Transit Path Choice Models, Perceived Utility, Behavioral Information Processing, Parameter Calibration
基于随机理论的公交路径选择建模
梁嘉贤1*,丘建栋1,潘嘉杰2
1深圳市城市交通规划设计研究中心有限公司,深圳
2广东省交通信息工程技术研究中心,深圳

收稿日期:2018年8月10日;录用日期:2018年8月22日;发布日期:2018年8月29日

摘 要
基于分层信息处理思想,运用随机理论框架下的公交路径选择模型,分析出行者在时空维度下的站点选择和公交车选择行为。以从广州市体育中心BRT站点到东圃镇BRT站点为例(共8条直达线路),利用IC卡数据和车辆报站数据对公交车感知效用函数进行参数标定和检验,结果表明,在对舒适度进行分层处理的情况下,候车时间、搭乘时间、站点舒适度、车内舒适度和搭乘线路经验均对公交路径选择具有显著性影响。
关键词 :公交路径选择,感知效用,行为信息处理,参数标定

Copyright © 2018 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
公交路径选择行为的研究可分为基于发车频率方法和基于时刻表方法。基于发车频率方法考虑公交线路集的服务情况,如公交车的发车间隔,但是它没有明确考虑公交车的运行时间。公交路径选择可基于最优策略路径的思想,使用基于发车频率方法实现。这种情况的前提假设是出行者永远以同一方式进行选择,如在最少感知出行时间的原则下,出行者总是搭乘线路选择集中第一辆到达的公交车,以避免由候车时间增加而使感知出行时间加大。在缺少出行信息和高频率公交服务的环境下,这种假设是可接受的。随着智能交通系统(ITS)的发展,现实生活中出行者不仅可在出发前获取路径信息,在出行途中,同样可通过移动设备等方式得到相应的实时出行信息(通过百度地图APP、Google地图APP等) [1][2]。此时,出行者的选择行为是根据当前条件的自适应选择 [3]。因此基于发车频率的方法缺乏考虑实时出行信息,在出行者候车时间、搭乘时间等因素的估算中均有所偏差,难以体现于现实生活中的真实出行。
基于时刻表的方法基于车辆到达和离开站点的时刻,考虑公交车服务的相关属性。Nuzzolo等 [4]将公交出行路径选择细分为站点选择和公交车辆选择。站点选择研究主要考虑了站点可达时间、附近商店数量、站点所能提供的车辆选择集等因素,以获取满足站点可达性和吸引力的最佳选项。线路和车辆选择不仅考虑了候车时间、搭乘时间等公交服务因素,还考虑了舒适度、可靠度等个体感受因素。Li等考虑了乘客搭乘时间、出行费用、不舒适度和公交服务可靠度的感知成本对乘客的出行选择行为进行描述 [5]。Nuzzolo等考虑了候车时间、搭乘时间、换乘时间、换乘次数、车内舒适度和站点舒适度构建车辆效用函数 [4][6]。Meignan等利用候车时间、步行时间、搭乘时间和出行经济成本来实现出行者行为建模 [7]。Hall等通过计算个体到达目的地的最少花费时间的期望值,包含了候车时间和上车搭乘时间,提出了一种随机且依赖于时间的出行时间的路径查询方法 [8]。Nuzzolo等不仅考虑了候车时间、搭乘时间、车内舒适度、换乘次数,还考虑了早/晚到达时间,即到达目的地的期望时间与实际时间的差异,和进入/离开公交服务的时间 [9]。
以上两类选择行为均可视为选择集生成和选择机理的综合作用结果,属于离散选择 [4]。选择集生成需要满足相应的约束,如个体偏好、是否可达,等以前k条个最优选项为原则生成相应的选择集,如最近的k个站点为站点选择集,最短的k条路径为线路选择集。选择机理用于评估选择集内选项的好坏。目前最常用的是由Von等建立的期望效用准则,认为出行者是理智的,会选择可选集合中效用最大的选项 [10]。但是由于出行者对路径信息掌握程度的差异,往往难以精确得到各个出行路径的实际效用,因此这种理论缺乏考虑个体对出行路径的感知误差 [11]。随机效用理论是Ben-Ariva等提出的,认为出行者对选项的感知效用是实际效用和随机项的综合,其中,随机项表示了个体的感知误差 [12]。前两种理论的一个局限是认为所有出行者均为最大效用选择者,同时选择集内的选项相互独立 [11]。Kahneman等提出了前景理论,认为个体会通过对比选择集内的选项与参考点之间的差异进行选择以相对收益和相对损失程度的角度来研究和分析决策者的风险态度 [13]。后悔理论是基于选择项的预期表现与非选择项胜过选择项的可能性对选项进行评估 [14][15]。前景理论和后悔理论已被广泛应用在经济学领域,近年也有交通领域的应用。
多项Logit和Probit随机离散模型最常用于个体出行路径选择行为的建模。Nuzzolo等通过提出diachronic图,全面分析站点感知效用和公交车感知效用,采用多项Logit模型实现了高频公交服务下,高频出行者(他们可根据出行经验了解公交服务运营情况)的动态路径选择模型 [4]。接着,作者在原来模型基础上,引入出发时间选择,考虑公交车容量的约束,采用多项Logit模型,提出拥挤公交网络下基于时刻表方法的分配模型 [6]。Nuzzolo等通过研究出行需求,提出了个人行为路径选择模型,并应用于个人出行规划助手中,通过意向调查结果对个体路径效用模型进行参数标定 [9],分析了使用多项Logit模型,混合Logit模型和巢式Logit模型的参数标定情况 [2]。尽管Logit系列模型标定较为简单方便,但是其IIA特性,使得概率结果可能出现不合理现象。Sheffi采用probit路径选择模型,通过随机元素的相关分析,获取具有共同弧段的路径相似度,并使用Monte Carlo方法计算路径选择概率 [16]。然而,Probit模型标定较为困难,应用比较费时。为了权衡标定和计算两方面指标,Cascetta等修正了多项Logit路径选择模型,并称为C-Logit模型,用于搭建路径选择行为,其基本思想是使用额外成本属性处理重叠路径的相似度 [17]。
在实际出行过程中,出行者可通过两种基本策略处理信息:分层处理和非分层处理 [18]。分层处理是由于人们大脑具有有限的能力处理复杂、高容量、零散数据信息,需要对信息进行分组,以方便处理。Fotheringham [19]提出了购物选择行为模型,中心思想是决策者很少可能会对比选择集中的所有选项,但是他们会对选项进行分类,再根据规则喜好等原因排除一些不需要的选择集,然后再使用合理的最大效用原则对剩余选项进行评估。Zhou Y等 [20]基于个人信息处理行为,提出了双层公交网络模型,分别面向出行者和实际计算中。在公交路径选择中,出行者需要综合考虑多个决策标准(如搭乘时间、换乘次数、换乘时间、步行、舒适度、安全性、出行目的等 [2][4][9][20]),在对每个决策标准的感知中,他们可以通过无线移动设备等获取准确的出行时间(包括搭乘时间、换乘次数、步行时间),但是部分属性无法准确地使用数值表示,同时他们也无需知道准确数值,如舒适度。在个人行为信息处理的分层思想中,他们将这些属性分类即可(舒适度从十分舒适到完全不舒适)。
因此本文提出了基于随机效用框架 [12]的公交路径选择模型,结合分层信息处理思想,考虑步行时间、候车时间、搭乘时间、可达线路、可达公交车等因素下,出行者在时间和空间维度中站点选择和公交车的感知效用和选择行为。最后以广州市从体育中心BRT站点和东圃镇BRT站点为例,利用IC卡数据和车辆报站数据对效用参数进行标定和检验,并分析了本次算例的存在问题。
2. 公交路径选择模型
公交路径选择模型根据出行者特点、交通系统特性和出行者行为假设,计算每一条可选路径的感知效用,进而为出行者提供合适的公交路径 [9]。一条公交路径是由一系列时空路段组成(如图1):在某天t的 时刻从起点O出发, 时刻到达候车站点s,等候时间为TW,在 时刻搭乘线路l的公交车r,接着与公交车r的时空路径重叠,直到在 时刻公交车到达下车站点s',出行者下车步行到达目的地(或进行换乘,重复候车搭乘阶段),最后在 时刻到达目的地D。
公交路径选择中,站点选择和公交车选择是主要组成部分。站点选择包括了初始上车站点的选择和
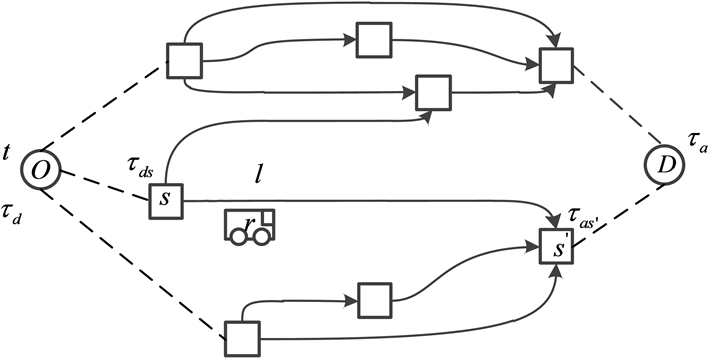
Figure 1. Path example
图1. 公交路径例子
换乘站点的选择,选择结果不仅影响着出行者本次出行的步行距离、步行时间,同时,站点所提供的线路(及相应的发车班次)限制了出行者的可达范围。公交车选择是出行者在选定并到达站点后,根据出行需求,选择搭乘的线路以及相应的公交车。根据这两种选择行为特性,可将出行者决策分为出行前选择和出行时的自适应选择。前者是出行者在出行前,根据出行者信息系统所提供的路径信息的决定,站点选择为典型的出行前选择。后者是指出行者不仅考虑出行前得到的静态信息,还考虑在出行途中所遇到情况的决策,如,线路和公交车选择。
结合以上两种选择(站点选择和公交车选择),公交路径选择模型可分为4个步骤:1) 路径选择集生成,2) 路径选择机理(效用)分析和计算,3) 学习过程,4) 模型参数标定。
2.1. 路径选择集
假设出行者在 时刻出发,从起点O到达终点D。首先需要步行到候车站点s。在给定od对下,站点选择集合 可定义为离出发地最近或在出行者设定的最大可忍受步行距离内的站点集合。
当出行者在 时刻到达站点s,此时可得到出行者的初始可达线路集合 ,这个集合符合当前时空约束,即初始可达线路集合是站点s提供线路,同时这些线路需满足在 时刻开始直到出行者到达目的地为止,仍处于运营状态。根据可达线路集合即可获得可选公交车集合 ,后者需要满足以下条件:1) 可直接或间接到达目的地,2) 出行者到达站点s后,每条属于可达线路集合 中的线路的第一辆到达站点车辆,3) 符合出行者设定规则,如最大换乘次数,最大出行时间等。
公交车集合 不仅依赖于出行者到达站点s的时刻 ,还会受到每一天的影响。则在同一天不同时刻到达站点s或在每一天同一时刻到达站点s所得到的公交车集合 是有所差异的,这是由于路面状况、线路发车班次等影响。
2.2. 路径选择机理
这里假设出行者是在出行前选择公交站点,在可选站点集合 中,每一个站点的感知效用 可表示为:
(1)
其中, 表示指定站点s的属性,包括步行到站时间、站点面积等。 表示服务站点s的公交车选择集合的内部效用,可理解为站点吸引力。 表示出行者i选择站点经验。 分别表示相应的属性。 为随机项。
对于公交车选择,假设出行者可通过站点提供的信息系统知道选择集中每一辆公交车的到站时间,或者出行者可通过自身经验感知获得每条线路的下一辆公交车的到站时间。出行者基于顺序选择行为,即根据公交车到达的先后,考虑到站车辆的感知效用与当前公交车选择集中其他车辆的感知效用,选取感知效用最大的公交车。注意,一旦公交车r到达站点,公交车选择集 被更新为 ,若该公交车没有被出行者选择, 同样会进行更新(将该辆公交车r从选择集中剔除,并将该车服务线路的下一辆车加入选择集中)。假设出行者在候车期间会自适应地选择某辆公交车r,由于该公交车在公交车选择集 中具有最大的感知效用 ,可表示为:
(2)
即在公交车r到达时,其它车辆r'仍未到达站点,且其相应车辆感知效用 均少于或等于公交车r的感知效用,则出行者选择自适应选择公交车r。
公交车感知效用 公式如下:
(3)
其中, 分别表示搭乘公交车r的候车时间和搭乘时间, 分别表示当前时刻站点s和公交车r的舒适度(或拥挤度)。 表示搭乘公交车r需要换乘次数。 表示出行者i选择该线路经验。 表示随机项。 均表示待标定参数。
2.3. 学习过程
结合站点感知效用 和车辆感知效用 ,出行者可利用自身经验和出行者信息系统等提供的信息来对本次出行进行决策。假设 表示在某一天t某时刻 ,所有站点、线路、公交车的相关属性(如感知效用的因素)。出行者可通过自身经验和路径效用信息等对这些属性进行学习感知。根据学习过程的差异,下面将上述属性(参数)分为3类:
1) 恒定属性 ,属性值不随时间而改变,如换乘次数 ,站点固定属性 。
2) 瞬时属性 ,这类属性是根据当前时刻的变化而更新,如候车时间 ,站点舒适度 。
3) 预测属性 ,这类属性可通过统计预测得到,如搭乘时间 ,车内舒适度 ,下一辆车舒适度 ,公交站点吸引力 。
因此,站点感知效用和车辆感知效用可写成由三类属性组成:
(4)
(5)
2.4. 参数标定
公交路径选择模型可应用于集计数据,也可应用于个人路径选择。前者可得到出行人群路径选择情况,为出行人群提供指引性信息,后者考虑个体出行偏好,可应用与出行助手等移动应用中,为用户提供可靠、符合喜好的出行选择。两者在参数标定上的差异是后者需要基于个体,对观测数据进行分类。
假设存在(单个或多个出行者的) N个观测样本,需要对离散选择模型进行参数估计。其中,样本数据包括公式中的每个参数(尤其是对瞬时属性和预测属性的获取),在相关文献中 [2][4][9]可通过意向调查获取,尽管调查数据可较好应用于参数的标定,但是意向调查不仅需要花费大量的人力物力,而且被调查者所填写的调查数据是否符合出行者实际出行行为还是有待商酌(尤其是对于不是经常乘坐公共交通的出行者,他们缺乏实际经验,在感知上,可能对每个参数的偏好程度有所偏差)。因此本文希望通过使用体现出行者实际出行行为的数据——IC卡数据和公交车辆报站数据,获取样本,从而实现参数标定。尽管在公交出行中,并不是所有出行者都使用IC卡,但是IC卡数据可以体现大部分人(尤其是高频出行人群)的出行选择行为。
公交车效用函数见公式(5),包含了搭乘时间、候车时间、站点舒适度、车内舒适度、搭乘经验。搭乘时间 计算见公式(6)。候车时间 根据车头时距可估算得到。根据同一线路和同一可达线路集合 分为平均最大车头时距 和平均最小车头时距 ,如公式(7)所示,前者假设出行者只搭乘同一线路的公交车,他的平均候车时间可近似为平均最大车头时距的一半。同样地,假设出行者较为理性(或者出行时间预算有限),他会搭乘可达线路集合的某一辆车,则他的平均候车时间可近似为平均最小车头时距的一半。
(6)
(7)
其中 表示线路l的公交车r到达站点s的时刻( , , 同理),站点s和s'表示为上下车站点,车辆r和r'表示前后两辆公交车。
公交车舒适度 可通过公交每辆车的平均载客人数与公交每辆车车内可供乘客使用的面积(一般为17.5平方米)的比值 [21]。但是这仅仅得到一个平均值,难以体现在3.3学习过程所提到的瞬时变化。因此,这里认为公交车的舒适度是由当前车辆载客数与车容量共同决定的(公式(8))。站点舒适度 可理解为出行者在候车期间站点的候车总人数与站点面积的比值(公式(8))。但是对于出行者来说,他们没有必要知道舒适度的准确数值,因为出行者对其不敏感,如同一辆车有5个人或10个人搭乘,计算结果中前者是后者的一半,但是对于出行者来说,两者的舒适度水平并不是一半的关系,因此这里将舒适度分为从十分舒适到十分不舒适,共5个选项,用0~4表示。
(8)
其中 分别表示公交车r在 时刻的载客量和公交车r的容量。 表示出行者在 时刻上车前的候车阶段中,在站点s的候车总人数, 表示站点s的面积。
站点经验 表示出行者是否根据经验出行选择公交车(公式(9))。
(9)
其中 , 和 可通过IC卡数据计算得到, 可通过公交车辆报站数据获得。
通过求出上述样本,选择multinomial Logit模型、Mixed Logit模型等,使用Biogeme2.2 [22]对模型参数标定。
3. 算例分析
为了验证公交路径决策模型的可行性,下面使用multinomial Logit模型,实现算例分析。由于无法得知站点效用的一些参数(如出发时间,步行时间),同时站点选择一般为出行前的选择行为,因此,本次算例只考虑出行者的公交车选择行为。
算例选用广州市体育中心BRT公交站和东圃镇BRT公交站为起点和终点,共8条直达线路,如表1所示,研究基于刷卡记录的乘客出行路径选择行为。起点和终点在可达线路的位置对车辆初始舒适度有所影响,如搭乘B3路,车辆舒适度不仅受途中上下车乘客的影响,还会被线路前面站点的上下车乘客数量所影响。其中IC刷卡数据和公交车辆报站数据使用的是从2014年3月10日到2014年3月16日共7天的数据。在实际出行中,出行者可以全面感知所选择路径,对于其他没有被选择路径,他们只能利
用自身经验的均值感知得到。因此,每条IC刷卡数据可视为一个选择,该选项的感知效用因素使用实际数据计算(详见2.4),其他选项均以由IC卡数据和报站数据分别统计得到的均值表示。根据2.4提到,对舒适度进行分层,表2为分层和不分层的模型参数标定结果(注意,由于8个选项中均为直达线路,这里没有将换乘次数进行标定)。
从表2可以看出,在将舒适度分层处理的情况下,在公交车选择行为中,车辆感知效用的各项因素均对公交车的决策具有显著影响。但是在不分层的情况下,以上因素对公交车选择的影响均不显著。同样地,在Nuzzolo [2][9]的算例中,无论使用Multinomial Logit模型和Mixed Logit模型,所得到的结果是候车时间、搭乘时间和期望到达时间对多公交模式的路径选择具有显著性,其它属性(如步行时间、舒适度、换乘次数)均未通过T检验。
对于本次算例得到的结果表明,在对公交路径选择模型进行标定时,各因素在不同方式处理下,可得到不一致的结果。主要原因可归为:1) 刷卡数据中需要对上下车站点进行估计,估计结果的误差可直接影响该记录的选择行为。2) 重新编码的误差,分层信息处理意味着要对数据划分范围并且重新编码,这会影响到结果的输出情况。3) 考虑因素的计算问题,在候车时间、舒适度的计算方法还有待改善。4) 本次选取的是7天的数据,对于第一天的某些记录,他们默认为没有搭乘经验,与现实不符合。
Table 1. Accessible routes in the case study
表1. 算例可达线路
Table 2. Attributes and parameters of bus choice models
表2. 公交车选择模型因素和参数标定结果
4. 结论
本文结合分层信息处理思想,使用公交路径选择模型,分析出行者在时空维度下的站点选择和公交车选择的感知效用。并以从广州市体育中心BRT站点到东圃镇BRT站点为例(共8条直达线路),利用IC卡数据和车辆报站数据对效用函数进行标定和检验,结果表明相同的数据,在对舒适度进行分层的情况下,考虑因素均对公交路径选择具有显著性影响,但是在不分层的情况下,结果相反。
结合算例的存在问题,本文在后期工作不仅需要继续完善数据的准确性和完整性,分析不同编码情况所引起的误差,考虑站点选择的标定和在公交车选择效用函数的标定中加入换乘次数等因素,更需要分析出行者在不同OD对下的公交路径选择行为的差异。同时,公交路径选择模型不仅可应用于集计情况下,随着先进公交出行者信息系统(Advanced Transit Traveller Information Systems (ATTIS))的完善,可应用于个人出行规划中,为出行者设置专有偏好的出行助手,提供在不同出行目的下符合个体感知效用的路径规划信息。
基金项目
深圳市科技计划项目(GGFW2016033017241891)资助;深圳市战略性新兴产业发展专项资金2017年第一批扶持计划(深发改[2017]550号)资助。
文章引用
梁嘉贤,丘建栋,潘嘉杰. 基于随机理论的公交路径选择建模
Modeling of Path Choice via Public Transit Based on the Random Theory[J]. 建模与仿真, 2018, 07(03): 173-181. https://doi.org/10.12677/MOS.2018.73021
参考文献
- 1. Zhang, L., Li, J.Q., Zhou, K., et al. (2011) Traveler Information Tool with Integrated Real-Time Transit Information and Multimodal Trip Planning: Design and Implementation. Transportation Research Record: Journal of the Transportation Research Board, 2215, 1-10. https://doi.org/10.3141/2215-01
- 2. Nuzzolo, A., Crisalli, U., Comi, A., et al. (2014) Advanced Trip Planners for Transit Networks: Some Theoretical and Experimental Aspects of Pre-Trip Path Choice Modeling. Computer-Based Modelling and Optimi-zation in Transportation. Springer International Publishing, Berlin, 405-417. https://doi.org/10.1007/978-3-319-04630-3_30
- 3. 李雨晴. 基于路况的公交路径寻优算法的研究与实现[D]: [硕士学位论文]. 北京: 北京邮电大学, 2013.
- 4. Nuzzolo, A., Russo, F. and Crisalli, U. (2001) A Doubly Dynamic Schedule-Based Assignment Model for Transit Networks. Transportation Science, 35, 268-285. https://doi.org/10.1287/trsc.35.3.268.10149
- 5. Li, Z.C., Lam, W.H.K. and Sumalee, A. (2008) Modeling Impact of Transit Operator Fleet Size under Various Market Regimes with Uncertainty in Network. Transportation Research Record, 44, 18-27. https://doi.org/10.3141/2063-03
- 6. Nuzzolo, A., Crisalli, U. and Rosati, L. (2012) A Schedule-Based Assignment Model with Explicit Capacity Constraints for Congested Transit Networks. Transportation Research Part C: Emerging Technologies, 20, 16-33. https://doi.org/10.1016/j.trc.2011.02.007
- 7. Meignan, D., Simonin, O. and Koukam, A. (2007) Simulation and Evaluation of Urban Bus Networks Using a Multiagent Approach. Simulation Modelling Practice & Theory, 15, 659-671. https://doi.org/10.1016/j.simpat.2007.02.005
- 8. Hall, R.W. (1986) The Fastest Path through a Network with Random Time-Dependent Travel Times. Transportation Science, 20, 182-188. https://doi.org/10.1287/trsc.20.3.182
- 9. Nuzzolo, A., Crisalli, U., Comi, A., et al. (2015) Individual Behavioural Models for Personal Transit Pre-Trip Planners. Transportation Research Procedia, 5, 30-43. https://doi.org/10.1016/j.trpro.2015.01.015
- 10. Von Neumann, J. and Morgenstern, O. (2007) Theory of Games and Economic Behavior. Princeton University Press, Hoboken.
- 11. Ramos, G.M., Daamen, W. and Hoogendoorn, S. (2014) A State-of-the-Art Review: Developments in Utility Theory, Prospect Theory and Regret Theory to Investigate Travellers’ Behaviour in Situations Involving Travel Time Uncertainty. Transport Reviews, 34, 46-67. https://doi.org/10.1080/01441647.2013.856356
- 12. Ben-Akiva, M.E. and Lerman, S.R. (1985) Discrete Choice Analysis: Theory and Application to Travel Demand. MIT Press, Cambridge, Massachusetts.
- 13. Kahneman, D. and Tversky, A. (1979) Prospect Theory: An Analysis of Decision under Risk. Econometrica: Journal of the Econometric Society, 47, 263-291. https://doi.org/10.2307/1914185
- 14. Bell, D.E. (1985) Disappointment in Decision Making under Uncertainty. Operations Re-search, 33, 1-27. https://doi.org/10.1287/opre.33.1.1
- 15. Loomes, G. and Sugden, R. (1982) Regret Theory: An Alternative Theory of Rational Choice under Uncertainty. The Economic Journal, 92, 805-824. https://doi.org/10.2307/2232669
- 16. Sheffi, Y. (1985) Urban Transportation Network: Equilibrium Analysis with Mathematical Programming Methods. Prentice Hall, Upper Saddle Riv-er.
- 17. Cascetta, E., Nuzzolo, A., Russo, F., et al. (1996) A Modified Logit Route Choice Model Overcoming Path Overlapping Problems: Specification and Some Calibration Results for Inter Urban Networks. In: Proceedings of the 13th International Symposium on Transportation and Traffic Theory, Pergamon, Oxford, 697-711.
- 18. Fotheringham, A.S. and Curtis, A. (1992) Encoding Spatial Information: The Evidence for Hierarchical Processing. Theories and Methods of Spatio-Temporal Reasoning in Geographic Space. Springer, Berlin Heidelberg, 269-287.
- 19. Fotheringham, A.S. (1988) Note-Consumer Store Choice and Choice Set Definition. Marketing Science, 7, 299-310. https://doi.org/10.1287/mksc.7.3.299
- 20. Zhou, Y., Thill, J.C. and Huang, Z. (2011) Design of a User-Centric Decision Support Tool for Fixed-Route Bus Travel Planning. Applied Geography, 31, 1173-1184. https://doi.org/10.1016/j.apgeog.2011.03.005
- 21. 边扬, 王炜, 陆建, 等. 城市出租车出行方式分担率预测方法研究[J]. 交通运输系统工程与信息, 2006, 6(2): 95-100.
- 22. Bi-erlaire, M. (2003) BIOGEME: A Free Package for the Estimation of Discrete Choice Models. Proceedings of the 3rd Swiss Trans-portation Research Conference, Ascona, 19-21 March 2003.
