一种36 kVA高频变压器的建模仿真与优化 Modeling and Optimization of a 36 kVA High-Frequency Transformer

doi:10.12677/MOS.2021.101008

Modeling and Simulation
Vol. 10 No. 01 ( 2021 ), Article ID: 40298 , 13 pages
10.12677/MOS.2021.101008

一种36 kVA高频变压器的建模仿真与优化

时振堂¹，李红叶¹，王志强²，刘征²

●How to Cite this Article

¹中国石化大连石油化工研究院，辽宁大连

²大连理工大学电气工程学院，辽宁大连

收稿日期：2020年11月17日；录用日期：2021年1月30日；发布日期：2021年2月7日

摘要

在直流输电、光伏发电、电力机车牵引等领域中，电力电子技术都是重要的支撑，而高频变压器是电力电子设备中的关键部分。近年来随着纳米晶体材料应用于高频变压器磁芯，变压器的性能取得了长足的提升。但是功率比较大的高频变压器在减小寄生参数、提升功率密度等方面的设计上仍存在比较多的难题。本文利用纳米晶体作为磁芯，基于一台36 kVA的10 kHz变压器对其进行建模分析研究，并对于总损耗和寄生参数进行了算法优化。最后应用计算机仿真检验了优化的可行性和有效性，对比得出最优的设计参数。

关键词

高频变压器，电磁仿真建模，优化

Modeling and Optimization of a 36 kVA High-Frequency Transformer

Zhentang Shi¹, Hongye Li¹, Zhiqiang Wang², Zheng Liu²

¹Sinopec Dalian Petrochemical Research Institute, Dalian Liaoning

²School of Electrical Engineering, Dalian University of Technology, Dalian Liaoning

Received: Nov. 17^th, 2020; accepted: Jan. 30^th, 2021; published: Feb. 7^th, 2021

ABSTRACT

In the fields of DC transmission, photovoltaic power generation and electric locomotive traction, the power electronic technology provides a critical support. Furthermore, the high-frequency transformer is a key component of the power electronic equipment. In recent years, with the application of nanocrystalline materials in manufacture of high-frequency transformers, the performance of transformers has been greatly improved. However, there are still many difficulties in the design of high-frequency transformers with relatively large power in terms of reducing parasitic parameters and increasing power density. This research uses the nanocrystalline as the magnetic core, modeling a 36 kVA transformer with10 kHz and making numerical optimization of total loss and parasitic parameters. Finally, computer simulation technology was used to verify the feasibility and validity of the optimization, and the optimal design parameters were obtained by the comparison.

Keywords:High-Frequency Transformer, Electromagnetic Modeling, Optimization

This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).

http://creativecommons.org/licenses/by/4.0/

1. 引言

随着电力电子技术的不断发展，高频开关电源、DC/DC变换器以及电力电子变压器(PET)等电力电子设备成为关注的热点 [1] [2]，在直流输电、光伏发电、电力机车牵引等领域应用前景广阔 [3] [4]。高频变压器是它们的关键组成部分，直接影响了设备的性能。高频变压器拥有效率高、体积小、重量轻等优点，对于实现电子设备的小型化和高效化有着重要的实际意义 [4]。但高频变压器相比于小功率变压器在设计上也存在更多的问题。在高频的工作状态下，变压器的漏感和寄生电容在高频下会引发暂态过程，破坏波形的稳定 [5]；集肤效应和邻近效应对于导体电阻产生不可忽视的影响 [6]；磁芯损耗需要更加复杂的模型来描述 [7]。所以高频变压器的理论分析与优化设计对于电力电子设备的发展十分重要。

本文以一台工作频率为10 kHz、额定功率为36 kVA的高频变压器为建模对象。基于高频方波激励下最大磁通密度选择方法，对磁芯损耗和绕组损耗的模型，漏感和寄生电容的影响及其理论分析进行了研究，建立了高频变压器的数学模型。运用乘子法分别进行高频变压器漏感和总损耗的优化。建立高频变压器的仿真模型，进行仿真计算，对比初步设计和优化后变压器的仿真结果，验证优化算法的可行性和有效性。

2. 高频变压器的建模

由于高频变压器广泛的应用于电力电子系统中，所以它的模型对于在相关电力电子系统的模拟分析和数值仿真时也具有重要的意义。本文选择用新兴的纳米晶体磁芯进行高频变压器的建模与设计，其电气参数如表1所示。

Table 1. High frequency transformer parameters

表1. 高频变压器参数

2.1. 高频变压器的数学模型

高频变压器的等效电路由于在高频条件下，漏感和寄生电容会引发暂态过程，影响到电压和电流波形的稳定以及电磁兼容的问题。所以漏感和寄生电容不能被随意忽略，要添加在等效电路上。高频变压器的一般等效电路如图1所示。

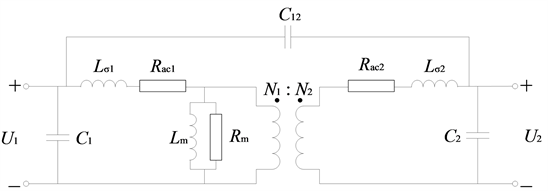
Figure 1. General equivalent circuits of the high frequency transformer

图1. 高频变压器一般等效电路

其中，U₁和U₂分别表示一次侧电压与二次侧电压，一、二次绕组的匝数分别为N₁和N₂，L_σ₁和L_σ₂分别表示一次与二次绕组的漏感，R_ac₁和R_ac₂分别表示一次与二次绕组的交流电阻，L_m和R_m分别表示励磁电感和铁损电阻，C₁和C₂分别表示一次与二次绕组的层间寄生电容，C₁₂表示一、二次绕组之间的寄生电容。可以对高频变压器一般等效电路进行一个化简，得到如图2所示的简化电路。

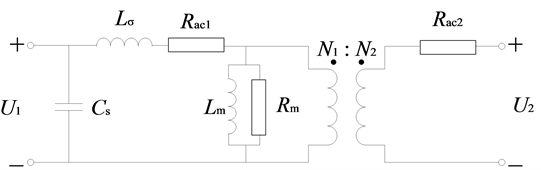
Figure 2. Simplified equivalent circuit of the High-frequency transformer

图2. 高频变压器简化等效电路

其中，L_σ表示换算到一次侧的总漏感，C_s表示换算到一次侧的总电容，它们与一般等效电路中的电路参量有如下关系。这两种等效电路都经常被用到，从电路参数的分布性角度考虑，显然一般等效电路更加准确。

$L_{σ} = L_{σ 1} + \frac{N_{1}^{2}}{N_{2}^{2}} L_{σ 2}$ (1)

$C_{s} = C_{1} + \frac{N_{2}^{2}}{N_{1}^{2}} C_{2} + {(\frac{N_{2}}{N_{1}} - 1)}^{2} C_{12}$ (2)

2.2. 最大磁通密度B_m的选择

对于高频变压器来说，存在一个最优的最大磁通密度使变压器的总损耗最小，也就是效率达到最大。可以在满足安全要求的基础上尽量选择靠近最优值的最大磁通密度B_m。

高频变压器计算铁损的公式为

$P_{c} = k_{c} f^{α} B_{m}^{β} V_{c} k_{f}$ (3)

高频变压器计算铜损的公式为

$P_{m} = R_{a c 1} I_{1}^{2} + R_{a c 2} I_{2}^{2} = F_{r 1} N_{1} \frac{ρ l_{m 1}}{S_{1}} I_{1}^{2} + F_{r 2} N_{2} \frac{ρ l_{m 2}}{S_{2}} I_{2}^{2}$

$( 5.35 )$

其中，F_r₁和F_r₂分别为一、二次绕组的交流电阻系数，l_m₁和l_m₂分别为一、二次绕组的平均匝长，S₁和S₂分别为一、二次绕组单匝裸导体的截面积。

根据高频变压器感应电动势的公式，一、二次绕组的匝数分别为

$N_{1} = \frac{U_{1}}{4 B_{m} A_{c} f}, N_{2} = \frac{U_{2}}{4 B_{m} A_{c} f}$ (4)

高频变压器的总损耗为

$P_{s} = P_{c} + P_{m}$ (5)

将总损耗的公式对最大磁通密度B_m求导，使导函数等于零的B_m就是要找到的最优值，用B_z来表示，计算的公式为

$B_{z}^{β + 1} = \frac{F_{r 1} U_{1} \frac{ρ l_{m 1}}{S_{1}} I_{1}^{2} + F_{r 2} U_{2} \frac{ρ l_{m 2}}{S_{2}} I_{2}^{2}}{4 A_{c} f^{α + 1} k_{m} β V_{c} k_{f}}$ (6)

在设计高频变压器时，除了考虑效率最优，还应当重点考虑安全问题，针对这两个方面的要求，选择合适的最大磁通密度B_m。根据前面对于剩磁影响的分析，由于纳米晶体磁芯饱和磁通密度为1.2 T，所以本课题所选择的最大磁通密度应该不大于0.3 T。

2.3. 建模与理论参数计算

选择纳米晶体材料的CC型磁芯，初选最大磁通密度B_m为0.3 T，电流密度J为2.5 A/mm²，窗口利用率K_u为0.4，根据设计的目标功率选择磁芯的规格如图3，表2，表3。

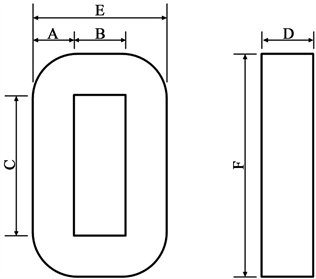
Figure 3. CC type with nanocrystal cores

图3. CC型纳米晶体磁芯

Table 2. Diameter of nanocrystalline CC cores

表2. 纳米晶体CC型磁芯的尺寸

Table 3. Parameters of nanocrystalline CC cores

表3. 纳米晶体CC型磁芯参数

高频变压器的电压调整率非常小，可以忽略掉。所以一、二次绕组的匝数为

$N_{1} = \frac{U_{1}}{4 B_{m} A_{c} f} = 48 匝$ (7)

$N_{2} = \frac{U_{2}}{4 B_{m} A_{c} f} = 16 匝$ (8)

一、二次侧额定电流为

$I_{1} = \frac{P}{U_{1}} = 40 A$ (9)

$I_{2} = \frac{P}{U_{2}} = 120 A$ (10)

绕组采用截面为矩形的铜导体来绕制，铜导体的集肤深度 $δ$ 为

$δ = \frac{66.1}{\sqrt{f}} = \frac{66.1}{\sqrt{10000}} = 0.661 mm$ (11)

一、二次绕组铜导体的截面积为

$S_{1} = \frac{I_{1}}{J} = 16 {mm}^{2}$ (12)

$S_{2} = \frac{I_{2}}{J} = 48 {mm}^{2}$ (13)

受到交流电流集肤效应和邻近效应的影响，在建模中一般要使导体的宽度小于集肤深度的二倍，来保证交流电阻系数不至于太大。所以一次侧绕组采用单股导体绕制，二次侧采用2股导体并绕。绕制一、二次侧绕组运用的铜导体参数如表4。

一次绕组分为6层，每层8匝；二次绕组分为4层，每层4匝。一、二次绕组分别平均分开绕在两个磁芯的两个柱上，所以每个柱上有3层一次绕组和2层二次绕组。一、二次绕组在两个柱上对称排布，一次绕组在内侧，二次绕组在外侧。绕组与磁芯间的环氧板绝缘厚度d_b为2 mm；绕组层间绝缘层厚度d_j应大于1.5 mm，这里选择2 mm进行建模；绕组外包绝缘厚度d_z为3 mm。

Table 4. Winding type and winding parameters

表4. 绕组铜导体参数和绕线方式

一、二次绕组以及绝缘层的高度为

$h_{1} = h_{2} = 104 \times 1.15 = 119.6 mm < 120 mm$ (14)

绕组高度小于窗口高度，是可行的。

绕组占窗口的总宽度d为

$d = (2 + 1.23 \times 3 + 0.92 \times 2 \times 2 + 2 \times 4 + 3) \times 2 = 40.74 mm < 45 mm$ (15)

绕组宽度小于窗口宽度，是可行的。

一、二次绕组的交流电阻系数为

$F_{r 1} = 6.08, F_{r 2} = 1.87$ (16)

一、二次绕组的直流电阻为

$R_{d c 1} = \frac{l_{1}}{γ S_{1}} = \frac{16 \times (196.43 + 216.73 + 237.02)}{5.8 \times 10^{7} \times 16} \times 100 = 0.0112 Ω$ (17)

$R_{d c 2} = \frac{l_{2}}{γ S_{2}} = \frac{8 \times (259.23 + 283.36)}{5.8 \times 10^{7} \times 48} \times 100 = 0.0037 Ω$ (18)

一、二次绕组的交流电阻为

$R_{a c 1} = F_{r 1} R_{d c 1} = 0.0681 Ω$ (19)

$R_{a c 2} = F_{r 2} R_{d c 2} = 0.0070 Ω$ (20)

在这里要特别说明的是，在确定参数的基础上高频变压器计算效率最优时的最大磁通密度B_z为0.46 T，这个值大于安全的限定值0.3 T，所以选择最大磁通密度B_m为0.3 T来设计变压器是最佳的。

绕组层间绝缘的相对介电常数 $ε_{r}$ 为2，磁芯在工作状态的相对磁导率 $μ_{r}$ 为25,000，变压器的励磁电感、漏感、寄生电容的理论计算结果如表5所示。

Table 5. Theoretical calculation parameters of high frequency transformer with equivalent circuits

表5. 高频变压器等效电路理论计算参数

可以看到变压器的寄生电容很小，在10 kHz的工作频率下可以忽略，在后面的性能计算中忽略寄生电容的影响。综上所述，初始设计高频变压器主要性能指标如表6，满足设计目标的要求。

Table 6. Performance of theoretical model of the high frequency transformer

表6. 理论模型下的高频变压器主要性能指标

3. 高频变压器的优化与仿真验证

第二部分明确了高频电压器的理论模型，分析了漏感、寄生电容的理论计算方法，给出了高频变压器各个性能指标的计算公式。在理论分析的基础上建立了高频变压器的数学模型并编写了模型的MATLAB程序，进行了高频变压器的建模，本部分直接选择乘子法进行高频变压器的优化与仿真验证。

3.1. 高频变压器优化方程

在功率较大的高频变压器中更加关注的是温升、总损耗以及电压、电流的波形稳定，所以优化目标相较小功率变压器有所不同。高频变压器的温升和总损耗其实是相关的，所以分别将总损耗P_s、漏感L_σ作为优化目标。

由于在高频变压器的设计中已经选择了最佳的最大磁通密度B_m，隐含了最优化的思想，不再将它作为优化变量。选择电流密度J和绕组层间距离d_j作为优化变量，即

$x = (J; d_{j}) \in ℝ^{2}$ (21)

优化总损耗P_s的优化方程为

$\min P_{s} ( x )$

$s .t . d (x) \leq 45$

$d_{1} (x) \leq 2 δ$

$d_{2} (x) \leq 4 δ$

$Δ τ (x) \leq 40$

$η \geq 0.99$

$Δ U (x) \leq 0.01$

$d_{j} \geq 1.5$

$J \leq 5$

优化漏感L_σ的优化方程为

$\min L_{σ} ( x )$

$s .t . d (x) \leq 45$

$d_{1} (x) \leq 2 δ$

$d_{2} (x) \leq 4 δ$

$Δ τ (x) \leq 40$

$η \geq 0.99$

$Δ U (x) \leq 0.01$

$d_{j} \geq 1.5$

$J \leq 5$

其中，不等式约束的参数指标有绕组占窗口的总宽度d、一、二次绕组铜导体的宽度d₁和d₂、温升∆τ、效率η、电压调整率∆U、绕组层间绝缘厚度d_j、电流密度J。

3.2. 高频变压器优化结果

运用乘子法分别对总损耗P_s、漏感L_σ进行优化。优化结果如表7。

Table 7. Optimization results

表7. 算法优化结果

由优化结果可知，优化漏感L_σ或总损耗P_s的最优值点x^*结果几乎是相同的，这是因为优化漏感要在绝缘允许的范围内缩小层间距以及导体的厚度，这也就起到了减小导体长度以及交流电阻系数的作用。优化后的主要性能指标如表8所示，漏感L_σ和总损耗P_s都缩小了30%左右，其它的性能指标也均得到了一定的提高，优化效果良好。

Table 8. Performance of the optimized high frequency transformer

表8. 算法优化后高频变压器主要性能指标

3.3. 仿真验证高频变压器优化结果

通过ANSYS MAXWELL进行高频变压器的仿真计算，验证总损耗优化效果。通过MATLAB中Simulink模块进行仿真计算，验证漏感优化效果。

在ANSYSMAXWELL软件中建立高频变压器仿真模型(如图4)，进行瞬态磁场仿真。高频变压器的绕组模型不能再采用想小功率变压器一样的集中参数模型，因为高频变压器的仿真重要体现出漏感的影响，所以绕组应当分层建立模型，如图5所示。其中，红色的为一次绕组，橙色的为二次绕组。

采用外电路的激励方式，由于高频变压器主要用于DC/DC变换器，所以在负载端要接入全波整流电路，外电路如图6所示。

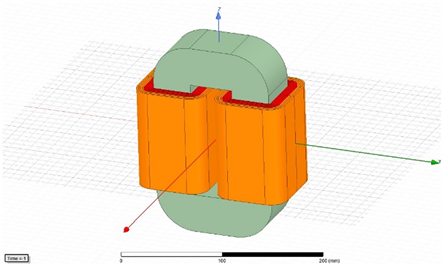
Figure 4. High frequency transformer model

图4. 高频变压器模型

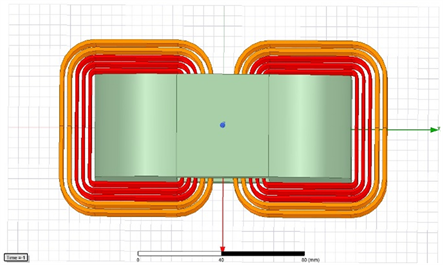
Figure 5. High frequency transformer winding model

图5. 高频变压器绕组模型

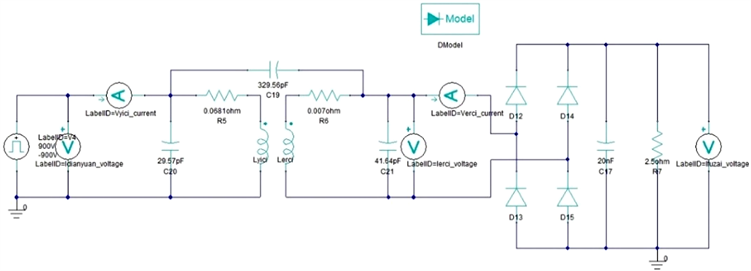
Figure 6. Excitation external circuit of high-frequency transformer (rated state)

图6. 高频变压器激励外电路(额定状态)

3.4. 初始高频变压器模型仿真结果

求解器类型选择瞬态磁场，初始设计高频变压器仿真计算，纳米晶体磁芯磁通密度分布如图7，图8。

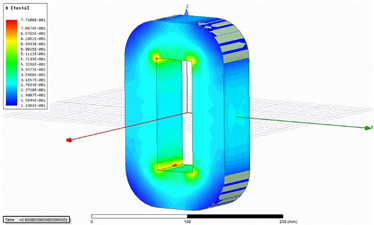
Figure 7. Flux density distribution of the high frequency transformer

图7. 高频变压器磁芯磁通密度分布

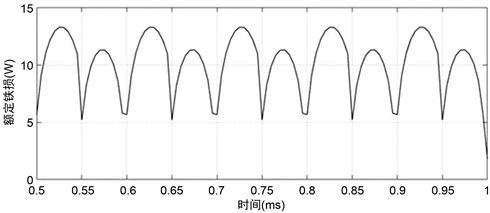
Figure 8. Iron loss waveform of the high frequency transformer

图8. 高频变压器铁耗波形

在方波激励下，额定负载状态电压、电流波形基本也是方波。仿真计算认为磁芯中初始无剩磁，所以磁通和励磁电流存在一个暂态过程，这与理论分析是一致的。初始设计高频变压器的各个电路参数仿真计算结果如表9，将用于计算高频变压器性能指标。

Table 9. Initial transformer simulation model circuit parameter

表9. 初始变压器仿真模型电路参量

初始设计高频变压器仿真计算的主要性能指标如表10。

Table 10. Performance of Initial Transformer simulation

表10. 初始变压器仿真性能指标

与理论计算结果十分接近，说明建立的高频变压器数学模型是合理的。

3.5. 优化后高频变压器仿真结果

对优化过总损耗P_s(W)的高频变压器进行仿真，改变绕组尺寸和外电路参数。优化后，高频变压器各个电路参数的仿真计算结果如表11。

Table 11. Optimized transformer simulation circuit parameters

表11. 优化后变压器仿真电路参量

经过仿真计算，优化后的高频变压器主要性能指标如表12。

Table 12. Performance of the optimized transformer simulation

表12. 优化后变压器仿真计算主要性能指标

将优化前后的仿真结果进行对比，总损耗减小了30%左右，与理论计算的结果相近，可知对总损耗的优化计算效果显著。

3.6. 检验漏感优化效果

运用Simulink建立高频变压器空载仿真电路，如图9所示。电路由直流逆变电路、高频变压器、整流电路三部分组成。

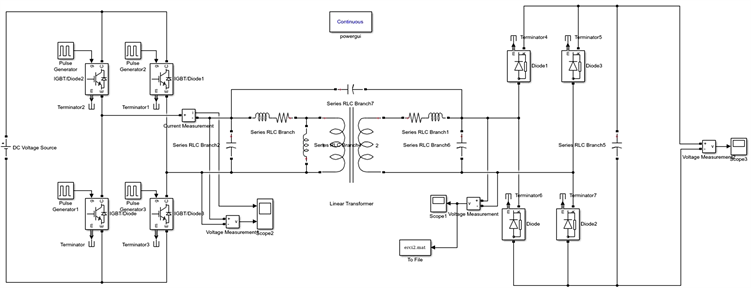
Figure 9. High-frequency transformer no-load simulation circuit

图9. 高频变压器空载仿真电路

初始设计和优化后高频变压器的分布参数按表13进行设置。

Table 13. Equivalent circuit distribution parameters for high frequency transformers

表13. 高频变压器等效电路分布参数

经过仿真计算，初始设计和优化漏感后空载二次侧电压波形如图10，图11。

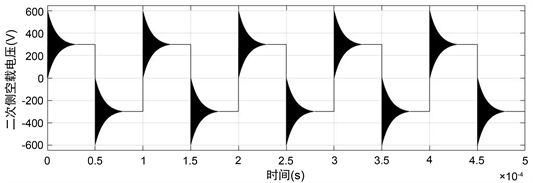
Figure 10. Secondary voltage waveform of initial model with no-load

图10. 初始模型空载二次侧电压波形图

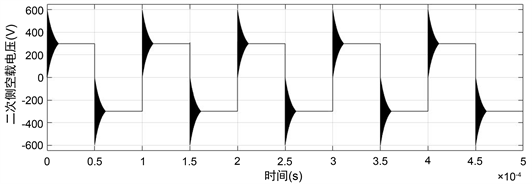
Figure 11. Secondary voltage waveform of optimized model with no-load

图11. 优化后模型空载二次侧电压波形图

由波形图可以看出优化漏感后，方波上升沿处的过电压过程明显缩短，对高频变压器漏感的优化计算是有效的。

4. 结论

本文从高频变压器的原理出发，分析了它们的不同特点，分别建立了数学模型，根据实际目标进行了初始建模。在此基础上，将数值最优化方法应用于变压器的优化设计中。依托计算机强大的数值计算能力，根据工程需要，有效提升变压器的性能指标。本文主要得出如下结论：

本文基于一台36 kVA的10 kHz变压器创建电气模型，选择最大磁通密度要从效率最优化和保证暂态过程安全运行两个方面考虑，结合实际参数对高频变压器的影响对其进行初步建模分析。运用乘子法分别对漏感和总损耗进行优化，发现优化得到的最优值点是相同。这是由于减小绕组层间距离、适当提高电流密度有助于减小电阻和漏磁场的能量。优化后漏感和总损耗都减小了30%左右。

文章引用

时振堂,李红叶,王志强,刘征. 一种36 kVA高频变压器的建模仿真与优化
Modeling and Optimization of a 36 kVA High-Frequency Transformer[J]. 建模与仿真, 2021, 10(01): 70-82. https://doi.org/10.12677/MOS.2021.101008

参考文献

1. 薛伟, 郑丽君, 高云广, 李婧, 张晓伟, 宋建成. 电力电子变压器中高频变压器的设计方法[J]. 电测与仪表, 2015, 52(23): 117-121.

2. Han, J.X., Kong, X.P., Li, P., Zhang, Z. and Yin, X.G. (2019) A Novel Low Voltage Ride through Strategy for Cascaded Power Electronic Transformer. Protection and Control of Modern Power Systems, 4, 1-12. https://doi.org/10.1186/s41601-019-0137-1

3. 曹小鹏. 大功率高频变压器优化设计[D]: [硕士学位论文]. 南京: 东南大学, 2018.

4. 叶栋. 高频变压器分布参数的确定及其影响分析[D]: [硕士学位论文]. 温州: 温州大学, 2018.

5. Balci, S., Sefa, I. and Altin, N. (2016) An Investigation of Ferrite and Nanocrystalline Core Materials for Medium-Frequency Power Transformers. Journal of Electronicmaterials, 45, 276-285.

6. 张宁. 高频变压器优化设计方法与应用研究[D]: [硕士学位论文]. 北京: 华北电力大学, 2016.

7. 张朋朋. 大功率高频开关电源变压器的优化设计[D]: [硕士学位论文]. 成都: 西南交通大学, 2009.

期刊菜单