ABSTRACT

In non-life insurance application research, the classical Bühlmann credibility model cannot effectively reflect the tail information of distribution, and the policy between the risks is not completely independent. Therefore, considering the common effect between risks and combining the credibility theory from the perspective of quantile, the quantile credibility models under common effect structure are studied, which further expands the classical credibility model.

Keywords:Common Effect, Orthogonal Projection, Quantile, Credibility Model

共同效应结构下的分位数信度模型

程纪^*，吴黎军^#

新疆大学，数学与系统科学学院，新疆 乌鲁木齐

收稿日期：2019年3月19日；录用日期：2019年4月3日；发布日期：2019年4月10日

摘 要

在非寿险应用研究中，经典的Bühlmann信度模型并不能充分利用数据尾部的信息，且保单之间的风险并不是完全独立的，因而考虑在分位数视角下结合信度理论，综合风险之间存在的共同效应，研究了具有共同效应的分位数信度模型，拓展了经典的信度模型。

关键词 :共同效应，正交投影，分位数，信度模型

Copyright © 2019 by authors and Hans Publishers Inc.

This work is licensed under the Creative Commons Attribution International License (CC BY).

http://creativecommons.org/licenses/by/4.0/

1. 引言

在保险实践研究中，针对特定的投保人，观察到 $n$ 年的索赔数据 $X_1,X_2,\cdots ,X_n$ ，假设在同一费率级别中每个投保人的风险水平可用一个风险参数 $\Theta$ 来表示，不同的投保人对应不同的 $\Theta$ ，且 $\Theta$ 的分布为 $\text{π}\left(\Theta \right)$ ，以此将风险差异进行量化。我们假设 $\Theta$ 的存在性，理想情形下第 $n+1$ 年应当收取个体保费(条件期望) ${\mu }_{n+1}\left(\Theta \right)=E\left(X_{n+1}|\Theta \right)$ ，而不是净保费 $$ 。

Bühlmann (1967) [1] 提出无分布信度模型，用经验数据的线性组合 ${\alpha }_0+{\displaystyle \sum _{i=1}^n{\alpha }_i{X}_i}$ 来逼近 ${\mu }_{n+1}\left(\theta \right)$ ，通过求解下面的期望损失函数：

得到最优信度保费。之后，Bühlmann和Straub (1970) [2] 将无分布信度模型延伸到自然权重的情形。但这些模型均要求所研究的保单数据独立同分布，同时个体风险之间相互独立，我们期待能够找到一种针对特定环境下对保单进行分组并计算每个保单第 $n+1$ 年的个体保费 ${\mu }_{n+1}\left(\theta \right)$ 的费率厘定方法。因此，Yeo and Valdez (2006) [3] 通过用随机变量刻画风险之间存在的某种共同效应(例如某种特定环境)，在这种特殊结构下研究了信度保费估计，而后温利民等分别研究了信度模型及回归信度模型在共同效应情况下的信度保费 [4] [5] 。更一般地，考虑保单风险之间的相依关系，打破经典的风险独立假设，张强等(2018) [6] 研究了平衡损失函数下具有相依结构的信度估计。

鉴于保险数据经常具有较强的鲁棒性，存在一些具有强影响的离群点，经典的Bühlmann信度模型并不能有效利用这些离群值的数据信息，而分位数方法能够很好地解决这一问题，Georgios Pitselis (2013) [7] 在风险独立性的假设下，用分位数技术首次建立了分位数信度模型，阐述了分位数与经典的Bühlmann信度与Hachemeister回归信度模型之间的联系，并将分位数纳入到这两大经典的信度模型中。本文综合考虑数据鲁棒性及风险之间的特定影响效应，创造性地建立了具有共同效应的分位数信度模型，致力于充分利用所有数据的信息，作出最佳的估计，从而实现保险产品结构的优化。

2. 模型假设与准备

2.1. 准备知识

考虑 $K$ 份保单合同，对于第 $i$ 份合同有 $n$ 年的索赔数据， $i=1,2,\cdots k$ ，则样本数据构成一个矩阵：

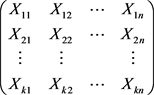
风险由风险参数 $\theta \in \Theta$ 进行描述，对任意 $p\in \left(0,1\right)$ ， $\xi$ 为概率空间 $\left(\Omega ,\Gamma ,{\rm P}\right)$ 上的随机变量，令 $\xi \left(p\right)=F^{-1}\left(p\right)=\inf \left\{x:F\left(x\right)\ge p\right\}$ 为 $\xi$ 的p−分位数。

在给定风险参数 $\Theta$ 下，第i份保单的索赔随机向量为 $X_i$ ， $X_i={\left(X_{i1},X_{i2},\cdots ,X_{in}\right)}^{\prime }$ ，设 $F_n\left(x\right)$ 为样本 $\left\{X_{i1},X_{i2},\cdots ,X_{in}\right\}$ 的经验分布函数，则样本P-分位数的估计可定义为：

$\widehat{\xi }\left(p\right)=n\left(\frac{j}{n}-p\right)X_{\left(j-1\right)}+n\left(p-\frac{j-1}{n}\right)X_{\left(j\right)},其中\frac{j-1}{n}\le p\le \frac{j}{n},j=1,\cdots ,n.$

记 $X={\left(X_1{}^{\prime },X_2{}^{\prime },\cdots ,X_k{}^{\prime }\right)}^{\prime }$ 为所有索赔数据组成的列向量， ${\widehat{\xi }}_{ij}\left(p\right)$ 为样本分位数的估计。我们的目标是通过对样本选取不同分位点，预测每份保单在各分位点第 $n+1$ 年的索赔。由于各保单之间存在某一特定效应，我们用随机变量 $\Lambda$ 来刻画此种共同效应，下面给出模型的基本假设。

2.2. 模型假设

假设1：风险之间存在共同效应 $\Lambda$ ，且 $E\left[\Lambda \right]={\mu }_{\lambda },Var\left[\Lambda \right]=S_{\lambda }^2.$

假设2：给定共同效应 $\Lambda$ ，风险参数 ${\Theta }_i$ ，索赔样本数据为 $X_{i1},X_{i2},\cdots ,X_{in}$ ，其样本分位数 ${\widehat{\xi }}_{ij}\left(p\right)$ 的条件期望和条件方差如下：

$E\left({\widehat{\xi }}_{ij}\left(p\right)|{\Theta }_i,\Lambda \right)={\Xi }_p\left({\Theta }_i,\Lambda \right),Var\left({\widehat{\xi }}_{ij}\left(p\right)|{\Theta }_i,\Lambda \right)=V_p\left({\Theta }_i,\Lambda \right).$

引入下列记号：

$\begin{array}{l}E\left[{\Xi }_P\left({\Theta }_i,\Lambda \right)|\Lambda \right]={\Xi }_1\left(p,\Lambda \right),Var\left[{\Xi }_P\left({\Theta }_i,\Lambda \right)|\Lambda \right]=S_2^2\left(p,\Lambda \right),\\ E\left[{\Xi }_1\left(p,\Lambda \right)\right]={\Xi }_1\left(p\right),E\left[S_2^2\left(p,\Lambda \right)\right]=S_2^2\left(p\right),Var\left[{\Xi }_1\left(p,\Lambda \right)\right]={\psi }_1\left(p\right),\\ E\left[V_p\left({\Theta }_i,\Lambda \right)|\Lambda \right]=S_1^2\left(p,\Lambda \right),E\left[S_1^2\left(p,\Lambda \right)\right]=S_1^2\left(p\right).\end{array}$

2.3. 模型求解

根据信度理论，我们用样本分位数的线性函数逼近最优信度保费，即求解最小化问题：

$\underset{A,B}{\min }E\left[\left(\Xi \left(p\right)-A-B\widehat{\xi }\left(p\right)\right){\left(\Xi \left(p\right)-A-B\widehat{\xi }\left(p\right)\right)}^{\prime }\right]$ (1)

式中，

$\begin{array}{l}\Xi \left(p\right)={\left[{\widehat{\xi }}_{1,n+1}\left(p\right),\cdots ,{\widehat{\xi }}_{K,n+1}\left(p\right)\right]}^{\prime }\\ \widehat{\xi }\left(p\right)={\left[{\widehat{\xi }}_1{\left(p\right)}^{\prime },\cdots ,{\widehat{\xi }}_K{\left(p\right)}^{\prime }\right]}^{\prime }\\ {\widehat{\xi }}_i\left(p\right)={\left[{\widehat{\xi }}_{i1}\left(p\right),\cdots ,{\widehat{\xi }}_{in}\left(p\right)\right]}^{\prime }\end{array}$

基于样本分位数， $\Xi \left(p\right)$ 的非齐次信度估计为 $\widehat{\Xi }\left(p\right)=\text{pro}\left[\Xi \left(p\right)|L\left(\widehat{\xi }\left(p\right),1\right)\right]$ ，本文利用正交投影法求解最优化问题(1)，引入下列引理。

引理1：设 $X={\left(X_1,\cdots ,X_n\right)}^{\prime }$ ， $Y={\left(Y_{１},\cdots ,Y_m\right)}^{\prime }$ 为两个随机向量， $Y$ 在 $L\left(X,1\right)$ 上的正交投影为

$\text{pro}\left(Y|L\left(X,1\right)\right)=E\left(Y\right)+Cov\left(Y,X\right)Co{v}^{-1}\left(X,X\right)(X-E(X))$

证明见Wen et al. (2009) [4] 。

引理2：设A，B，C，D为适当阶数的矩阵，且A，C可逆，则有求逆公式：

${\left(A+BCD\right)}^{-1}=A^{-1}-A^{-1}B{\left(C^{-1}+D{A}^{-1}B\right)}^{-1}D{A}^{-1}$

证明：由

$\begin{array}{l}\left(A+BCD\right)\left[A^{-1}-A^{-1}B{\left(C^{-1}+D{A}^{-1}B\right)}^{-1}D{A}^{-1}\right]\\ =I-B{\left(C^{-1}+D{A}^{-1}B\right)}^{-1}D{A}^{-1}+BCD{A}^{-1}-BCD{A}^{-1}B{\left(C^{-1}+D{A}^{-1}B\right)}^{-1}D{A}^{-1}\\ =I+BCD{A}^{-1}-B\left(I+CD{A}^{-1}B\right){\left(C^{-1}+D{A}^{-1}B\right)}^{-1}{C}^{-1}CD{A}^{-1}\\ =I+BCD{A}^{-1}-B\left(I+CD{A}^{-1}B\right){\left(I+CD{A}^{-1}B\right)}^{-1}CD{A}^{-1}\\ =I+BCD{A}^{-1}-BCD{A}^{-1}\\ =I\end{array}$

即

${\left(A+BCD\right)}^{-1}=A^{-1}-A^{-1}B{\left(C^{-1}+D{A}^{-1}B\right)}^{-1}D{A}^{-1}$

引理3：在模型假设1和假设2下，有以下结果：

1) ${\widehat{\xi }}_i\left(p\right)={\left[{\widehat{\xi }}_{i1}\left(p\right),\cdots ,{\widehat{\xi }}_{in}\left(p\right)\right]}^{\prime }$ 的期望为：

$E\left[{\widehat{\xi }}_i\left(p\right)\right]={\Xi }_1\left(p\right)1_n.$

其中 $1_n$ 为所有元素均为1的n维列向量。

2) 向量 $\widehat{\xi }\left(p\right)={\left[{\widehat{\xi }}_1{\left(p\right)}^{\prime },\cdots ,{\widehat{\xi }}_K{\left(p\right)}^{\prime }\right]}^{\prime }$ 的协方差矩阵为：

$Cov\left[\widehat{\xi }\left(p\right),\widehat{\xi }\left(p\right)\right]=I_k\otimes \left(S_1^2\left(p\right)I_n+S_2^2\left(p\right)1_n{1^{\prime }}_n\right)+{\psi }_1\left(p\right)1_{nk}{1^{\prime }}_{nk}.$

3) 矩阵 $Cov\left[\widehat{\xi }\left(p\right),\widehat{\xi }\left(p\right)\right]$ 的逆矩阵为：

$\begin{array}{c}Co{v}^{-1}\left[\widehat{\xi }\left(p\right),\widehat{\xi }\left(p\right)\right]=\frac{1}{S_1^2\left(p\right)}{I}_k\otimes \left(I_n-\frac{S_2^2\left(p\right)}{S_1^2\left(p\right)+n{S}_2^2\left(p\right)}{1}_n{1^{\prime }}_n\right)\\ -\frac{{\psi }_1\left(p\right)}{\left[S_1^2\left(p\right)+n{S}_2^2\left(p\right)\right]\left[S_1^2\left(p\right)+n{S}_2^2\left(p\right)+nk{\psi }_1\left(p\right)\right]}{1}_{nk}{1^{\prime }}_{nk}.\end{array}$

4) $\Xi \left(p\right)={\left[{\widehat{\xi }}_{1,n+1}\left(p\right),\cdots ,{\widehat{\xi }}_{K,n+1}\left(p\right)\right]}^{\prime }$ 与 $\widehat{\xi }\left(p\right)={\left[{\widehat{\xi }}_1{\left(p\right)}^{\prime },\cdots ,{\widehat{\xi }}_K{\left(p\right)}^{\prime }\right]}^{\prime }$ 的协方差矩阵为

$Cov\left[\Xi \left(p\right),\widehat{\xi }\left(p\right)\right]=\left(S_2^2\left(p\right){e^{\prime }}_i+{\psi }_1\left(p\right){1^{\prime }}_k\right)\otimes {1^{\prime }}_n.$

证明：

1)

$E\left[{\widehat{\xi }}_i\left(p\right)\right]=E[\left[\left(E{\widehat{\xi }}_i\left(p\right){|\Theta }_i,\Lambda \right)\right]=E\left(\begin{array}{c}E\left({\Xi }_p\left({\Theta }_i,\Lambda \right)|\Lambda \right)\\ ⋮\\ E\left({\Xi }_p\left({\Theta }_i,\Lambda \right)|\Lambda \right)\end{array}\right)=E\left(\begin{array}{c}{\Xi }_1\left(p,\Lambda \right)\\ ⋮\\ {\Xi }_1\left(p,\Lambda \right)\end{array}\right)={\Xi }_1\left(p\right)1_n.$

2) 记 $\Theta ={\left({\Theta }_1,\cdots ,{\Theta }_k\right)}^{\prime }$ ，则

$\begin{array}{l}E\left[\widehat{\xi }\left(p\right)|\Theta ,\Lambda \right]\text{=[}{\Xi }_p\left({\Theta }_1,\Lambda \right){\text{<msup> <mo> 1</mo> <mo> ′ </mo> </msup>}}_n\text{,}\cdots \text{,}{\Xi }_p\left({\Theta }_k,\Lambda \right){\text{<msup> <mo> 1</mo> <mo> ′ </mo> </msup>}}_n\text{<msup> <mo> ] </mo> <mo> ′ </mo> </msup>}={\left[{\Xi }_p\left({\Theta }_1,\Lambda \right)\text{,}\cdots \text{,}{\Xi }_p\left({\Theta }_k,\Lambda \right)\right]}^{\prime }\otimes {\text{1}}_n\\ Cov\left[\widehat{\xi }\left(p\right)|\Theta ,\Lambda \right]=\text{diag}\left[V_p\left({\Theta }_1,\Lambda \right)I_n\text{,}\cdots \text{,}{V}_p\left({\Theta }_k,\Lambda \right)I_n\right]\\ Cov\left[\widehat{\xi }\left(p\right),\widehat{\xi }\left(p\right)\right]=Cov\left[E\left(\widehat{\xi }\left(p\right)|\Theta ,\Lambda \right)\right]+E\left[Cov\left(\widehat{\xi }\left(p\right)|\Theta ,\Lambda \right)\right]\triangleq {{\rm I}}_1+{{\rm I}}_2\end{array}$

分项计算得：

$\begin{array}{c}{{\rm I}}_1=Cov\left[E\left(\widehat{\xi }\left(p\right)|\Theta ,\Lambda \right)\right]\\ =E\left(Cov\left\{{\left[{\Xi }_p\left({\Theta }_1,\Lambda \right),\cdots ,{\Xi }_p\left({\Theta }_k,\Lambda \right)\right]}^{\prime }\otimes 1_n|\Lambda \right\}\right)+Cov\left(E\left\{{\left[{\Xi }_p\left({\Theta }_1,\Lambda \right),\cdots ,{\Xi }_p\left({\Theta }_k,\Lambda \right)\right]}^{\prime }\otimes 1_n|\Lambda \right\}\right)\\ =E\left[S_2^2\left(p,\Lambda \right)\right]I_k\otimes 1_n{1^{\prime }}_n+Cov\left[{\Xi }_1\left(p,\Lambda \right)1_{nk}\right]\\ =S_2^2\left(p\right)I_k\otimes 1_n{1^{\prime }}_n+{\psi }_1\left(p\right)1_{nk}{1^{\prime }}_{nk}\\ {{\rm I}}_2=E\left[Cov\left(\widehat{\xi }\left(p\right)|\Theta ,\Lambda \right)\right]=S_1^2\left(p\right)I_{nk}\end{array}$

则有，

$Cov\left[\widehat{\xi }\left(p\right),\widehat{\xi }\left(p\right)\right]\triangleq {{\rm I}}_1+{{\rm I}}_2=I_k\otimes \left(S_1^2\left(p\right)I_n+S_2^2\left(p\right)1_n{1^{\prime }}_n\right)+{\psi }_1\left(p\right)1_{nk}{1^{\prime }}_{nk}$

3) 根据引理2得

$\begin{array}{c}{\left(S_1^2\left(p\right)I_n\text{+}{S}_2^2\left(p\right)1_n{1^{\prime }}_n\right)}^{-1}=\frac{1}{S_1^2\left(p\right)}{I}_n-\frac{\left(p\right)1_n{1^{\prime }}_n}{\frac{1}{S_2^2\left(p\right)}+\frac{1}{S_1^2\left(p\right)}{1}_n{1^{\prime }}_n}\\ =\frac{1}{S_1^2\left(p\right)}\left(I_n-\frac{S_2^2\left(p\right)}{S_1^2(p)+n{S}_2^2\left(p\right)}{1}_n{1^{\prime }}_n\right)\end{array}$

因此， ${\left(S_1^2\left(p\right)I_n+S_2^2\left(p\right)1_n{1^{\prime }}_n\right)}^{-1}{1}_n=\frac{1}{S_1^2\left(p\right)+n{S}_2^2\left(p\right)}{1}_n.$

因为 $$

所以，

$\begin{array}{c}Co{v}^{-1}[\widehat{\xi }\left(p\right),\widehat{\xi }\left(p\right)]=I_k\otimes {\left(S_1^2\left(p\right)I_n\text{+}{S}_2^2\left(p\right)1_n{1^{\prime }}_n\right)}^{-1}\\ -\frac{\left[I_k\otimes {\left(S_1^2\left(p\right)I_n\text{+}{S}_2^2\left(p\right)1_n{1^{\prime }}_n\right)}^{-1}\right]1_{nk}{1^{\prime }}_{nk}\left[I_k\otimes {\left(S_1^2\left(p\right)I_n\text{+}{S}_2^2\left(p\right)1_n{1^{\prime }}_n\right)}^{-1}\right]}{\frac{1}{{\psi }_1\left(p\right)}+{1^{\prime }}_{nk}\left[I_k\otimes {\left(S_1^2\left(p\right)I_n\text{+}{S}_2^2\left(p\right)1_n{1^{\prime }}_n\right)}^{-1}\right]1_{nk}}\\ =\frac{1}{S_1^2\left(p\right)}{I}_k\otimes \left(I_n-\frac{S_2^2\left(p\right)}{S_1^2\left(p\right)+n{S}_2^2\left(p\right)}{1}_n{1^{\prime }}_n\right)\\ -\frac{{\psi }_1\left(p\right)}{\left[S_1^2\left(p\right)+n{S}_2^2\left(p\right)\right]\left[S_1^2\left(p\right)+n{S}_2^2\left(p\right)+nk{\psi }_1\left(p\right)\right]}{1}_{nk}{1^{\prime }}_{nk}.\end{array}$

4) 因为 $Cov\left(\Xi \left(p\right),\widehat{\xi }\left(p\right)|\Theta ,\Lambda \right)=0$ ，则

$\begin{array}{c}Cov\left[\Xi \left(p\right),\widehat{\xi }\left(p\right)\right]=Cov\left[E\left(\Xi \left(p\right)|\Theta ,\Lambda \right),E\left(\widehat{\xi }\left(p\right)|\Theta ,\Lambda \right)\right]+E\left[Cov\left(\Xi \left(p\right),\widehat{\xi }\left(p\right)|\Theta ,\Lambda \right)\right]\\ =Cov\left\{{\Xi }_p\left({\Theta }_i,\Lambda \right),{\left[{\Xi }_p\left({\Theta }_1,\Lambda \right),\cdots ,{\Xi }_p\left({\Theta }_k,\Lambda \right)\right]}^{\prime }\otimes 1_n\right\}\\ =E\left(Cov\left\{{\Xi }_p\left({\Theta }_i,\Lambda \right),{\left[{\Xi }_p\left({\Theta }_1,\Lambda \right),\cdots ,{\Xi }_p\left({\Theta }_k,\Lambda \right)\right]}^{\prime }\otimes 1_n|\Lambda \right\}\right)\\ +Cov\left(E\left[{\Xi }_p\left({\Theta }_i,\Lambda \right)|\Lambda \right],{\left\{E\left[{\Xi }_p\left({\Theta }_1,\Lambda \right)|\Lambda \right],\cdots ,E\left[{\Xi }_p\left({\Theta }_k,\Lambda \right)|\Lambda \right]\right\}}^{\prime }\otimes 1_n\right)\\ =S_2^2\left(p\right){e^{\prime }}_i\otimes {1^{\prime }}_n+Cov\left[{\Xi }_1\left(p,\Lambda \right),{\Xi }_1\left(p,\Lambda \right)1_{nk}\right]=S_2^2\left(p\right){e^{\prime }}_i\otimes {1^{\prime }}_n+{\psi }_1\left(p\right){1^{\prime }}_{nk}\\ =\left(S_2^2\left(p\right){e^{\prime }}_i+{\psi }_1\left(p\right){1^{\prime }}_k\right)\otimes {1^{\prime }}_n\end{array}$

引理3证毕。

3. 具有共同效应结构的分位数信度模型

定理3.1：在模型假设1及假设2下，求解最小化问题(1)可得 ${\Xi }_P\left(\Theta \right)$ 的最优线性信度估计为

$\widehat{\Xi }\left(p\right)=Z_1\overline{\widehat{\xi }}\left(p\right)+Z_2\overline{\overline{\widehat{\xi }}}\left(p\right)+Z_3{\Xi }_1(p)$

式中，

$\begin{array}{l}{Z}_1=\frac{n{S}_2^2\left(p\right)}{n{S}_2^2\left(p\right)+S_1^2\left(p\right)},\\ Z_2=\frac{nk{\psi }_1\left(p\right)S_1^2\left(p\right)}{\left[n{S}_2^2\left(p\right)+S_1^2\left(p\right)\right]\left[nk{\psi }_1\left(p\right)+n{S}_2^2\left(p\right)+S_1^2\left(p\right)\right]},\\ Z_3=1-Z_1-Z_2=\frac{S_1^2\left(p\right)}{nk{\psi }_1\left(p\right)+n{S}_2^2\left(p\right)+S_1^2\left(p\right)}.\end{array}$

为信度因子。

其中，

${\overline{\widehat{\xi }}}_i\left(p\right)=\frac{1}{n}{\displaystyle \sum _{j=1}^n{\widehat{\xi }}_{ij}\left(p\right)},\overline{\overline{\widehat{\xi }}}\left(p\right)=\frac{1}{k}{\displaystyle \sum _{i=1}^k{\overline{\widehat{\xi }}}_i\left(p\right)}.$

证明：由引理1及引理3得

$\begin{array}{c}\widehat{\Xi }\left(p\right)=E\left[\Xi \left(p\right)\right]+Cov\left[\Xi \left(p\right),\widehat{\xi }\left(p\right)\right]Co{v}^{-1}\left[\widehat{\xi }\left(p\right),\widehat{\xi }\left(p\right)\right]\left[\widehat{\xi }\left(p\right)-E\left(\widehat{\xi }\left(p\right)\right)\right]\\ ={\Xi }_1\left(p\right)+\frac{1}{n{S}_2^2\left(p\right)+S_1^2\left(p\right)}\left[S_2^2\left(p\right){e^{\prime }}_i\otimes {1^{\prime }}_n+\frac{{\psi }_1\left(p\right)S_1^2\left(p\right)}{nk{\psi }_1\left(p\right)+n{S}_2^2\left(p\right)+S_1^2\left(p\right)}{1^{\prime }}_{nk}\right]\left[\widehat{\xi }\left(p\right)-{\Xi }_1\left(p,\Lambda \right)1_{nk}\right]\\ ={\Xi }_1\left(p\right)+\frac{1}{n{S}_2^2\left(p\right)+S_1^2\left(p\right)}\left[n{S}_2^2\left(p\right)\left(\overline{{\widehat{\xi }}_i}\left(p\right)-{\Xi }_1\left(p\right)\right)+\frac{nk{\psi }_1\left(p\right)S_1^2\left(p\right)}{nk{\psi }_1\left(p\right)+n{S}_2^2\left(p\right)+S_1^2\left(p\right)}\left(\overline{\overline{\stackrel{\wedge }{\xi }}}\left(p\right)-{\Xi }_1\left(p\right)\right)\right]\\ =Z_1\overline{{\widehat{\xi }}_i}\left(p\right)+Z_2\overline{\overline{\widehat{\xi }}}\left(p\right)+Z_3{\Xi }_1(p)\end{array}$

定理3.1得证。

4. 总结

本文在分位数的视角下，结合信度理论，建立了共同效应结构下的分位数信度模型。通过自由选择样本分位点打破了经典的信度模型中数据鲁棒性的弊端，利用随机变量反映风险之间的共同效应，解决实际应用中保单风险并不独立的情形，得到了最优的信度保费，从而降低经营风险，使得保险产品真正回归到保障本质。

致谢

感谢国家自然科学基金课题“基于分位数回归的信度理论与风险度量的研究”(11861064)的资助，为本研究工作提供了良好的平台；感谢课题组导师在课题研究中无微不至地传道、授业、解惑，使我不断进步；感谢课题组成员对我的帮助、关心，伴我一路成长。

文章引用

程 纪,吴黎军. 共同效应结构下的分位数信度模型
Quantile Credibility Models under Common Effect Structure[J]. 统计学与应用, 2019, 08(02): 270-276. https://doi.org/10.12677/SA.2019.82030

参考文献