Advances in Applied Mathematics
Vol.05 No.01(2016), Article ID:16977,8
pages
10.12677/AAM.2016.51008
A Primal-Dual Polynomial Interior Point Method for Portfolio Investment without Short Sale
Zhenming Tian, Xinyu Song
School of Economics & Management, Guangzhou University of Chinese Medicine, Guangzhou Guangdong

Received: Feb. 4th, 2016; accepted: Feb. 21st, 2016; published: Feb. 24th, 2016
Copyright © 2016 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
Based on the optimal approach of Markowitz portfolio investment model, the algorithm of primal- dual polynomial interior point method to the above model was given. We applied this algorithm to solve an example of portfolio investment without short sale. Numerical implementation showed this method was practicable and effective.
Keywords:Portfolio, Quadratic Programming, Interior Point Method

不允许卖空证券组合投资模型的原始–对偶多项式内点算法
田振明,宋馨雨
广州中医药大学经济与管理学院,广东 广州

收稿日期:2016年2月4日;录用日期:2016年2月21日;发布日期:2016年2月24日

摘 要
在分析Markowitz证券组合投资模型最优化解法的基础上,给出了求解不允许卖空证券组合投资模型的原始–对偶多项式内点算法;不同于传统牛顿法的迭代方向,借助一种新的工具寻找搜索方向,并且该算法具有多项式复杂性;用我们给出的算法对不允许卖空证券组合投资模型的实例进行计算求解,数值结果显示该算法是可行有效的。
关键词 :证券组合,二次规划,内点算法

1. 引言
在证券组合理论研究和管理实践中,Markowitz证券组合投资模型理论[1] [2] 既是现代证券组合理论的奠基石,也是整个现代金融经济理论的奠基石。它不但在理论上使金融经济学从此改观,并且还在证券市场上引起一场“华尔街革命”。今天人们在处理证券组合投资的收益–风险分析时,Markowitz证券组合理论始终是一种基本工具。无论方差矩阵是非奇异矩阵情形的研究工作 [3] - [5] ,还是方差矩阵是奇异矩阵情形的研究工作 [6] - [9] ,均将Markowitz证券组合投资问题转化为一个目标函数是二次凸函数,约束条件是两个仿射等式约束的二次凸规划问题来进行求解。
Markowitz理论的基本思想在于把证券投资的收益率看作随机变量,于是该收益率的期望值就是该证券的期望收益,其标准差则可看作证券投资风险的一种度量。证券组合的收益率可表示为组合中所包含的证券的收益率的仿射组合,于是证券组合的期望收益等于其包含的各种证券的期望收益的仿射组合。其投资风险就是该仿射组合的收益率的标准差。对仿射组合的系数解最优化问题:对固定的期望收益,使其方差最小,或对固定的方差,使期望收益最大,就形成Markowitz理论的基本问题。基本问题的解称之为极小风险组合,也称为前沿组合。前沿组合的全体或其在风险和收益坐标平面上对应的点集称为组合前沿。在风险–收益坐标平面上,以“收益大,风险小”作为半序。那么所有组合的风险和收益对该半序来说的极大元全体就形成这一证券组合选择问题的有效前沿。有效前沿中的点所对应的组合则称为证券集的有效组合,确定证券投资组合的有效组合对投资者显然是十分重要的。
本文是在分析Markowitz证券组合选择模型最优化解法的基础上,给出了求解不允许卖空证券组合投资模型的原始–对偶多项式内点算法;不同于传统牛顿法的迭代方向,借助于一种新的工具找到搜索方向,并且该算法具有多项式复杂性;用我们给出的算法对不允许卖空证券组合投资模型的实例进行计算求解,数值计算结果显示该算法是可行有效的。
2. 不允许卖空Markowitz证券组合选择模型及预备知识
假设投资者选择市场上 种风险证券组成的集合
种风险证券组成的集合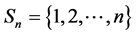 ,收益率期望值组成的向量记为
,收益率期望值组成的向量记为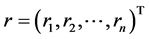 ;投资者投资此
;投资者投资此 种证券的证券组合权系数向量记为
种证券的证券组合权系数向量记为 ;两证券收益率的协方差记为
;两证券收益率的协方差记为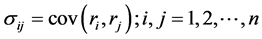 ,其对应的协方差矩阵为
,其对应的协方差矩阵为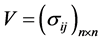 ,特别记向量
,特别记向量 ,该证券组合的收益率期望值为
,该证券组合的收益率期望值为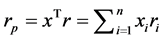 ,总风险记为
,总风险记为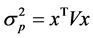 。沿用Markowitz
。沿用Markowitz
经典假设:1) 投资者事先知道证券收益率的概率分布;2) 投资风险用证券组合收益率的方差来标识;3) 影响投资决策的主要因素为证券组合的期望收益率和风险两项;4) 投资者遵守占优原则:同一风险水平下,选择收益率较高的证券组合;同一收益水平下,选择风险较低的证券组合。不允许卖空的Markowitz证券组合投资问题可叙述为如何确定 ,使得证券组合在期望收益率
,使得证券组合在期望收益率 时,风险最小,那么不允许卖空的Markowitz证券组合投资模型为
时,风险最小,那么不允许卖空的Markowitz证券组合投资模型为
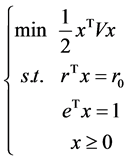 (1)
(1)
若协方差矩阵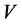 是非奇异矩阵,使用lagrange乘子法可得到模型(1)的最优解 [11] 为
是非奇异矩阵,使用lagrange乘子法可得到模型(1)的最优解 [11] 为 ,其中
,其中 ,
, 。另外,
。另外, ,
, ,
, ,
,
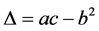 。若方差矩阵
。若方差矩阵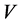 是奇异矩阵,可采用矩阵分解的方法得到模型(1)的最优解 [10] ,而且从求解过程可以发现,非奇异方差矩阵对应的证券组合投资决策模型的解是奇异矩阵下该模型解的一种特殊情形。本文在上述最优化理论与方法的分析基础上,给出求解不允许卖空Markowitz证券组合投资模型的原始-对偶多项式内点算法,下面首先引入一个重要的引理。
是奇异矩阵,可采用矩阵分解的方法得到模型(1)的最优解 [10] ,而且从求解过程可以发现,非奇异方差矩阵对应的证券组合投资决策模型的解是奇异矩阵下该模型解的一种特殊情形。本文在上述最优化理论与方法的分析基础上,给出求解不允许卖空Markowitz证券组合投资模型的原始-对偶多项式内点算法,下面首先引入一个重要的引理。
引理(K-K-T条件) [12] 对于最优化问题
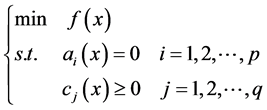
其中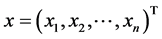 ,
,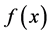 ,
,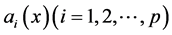 与
与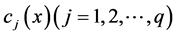 具有连续的一阶偏导数。若
具有连续的一阶偏导数。若 是该问题的局部最优解,则存在常数
是该问题的局部最优解,则存在常数 ,
, 使得
使得

特别地,当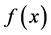 为凸函数,可行域
为凸函数,可行域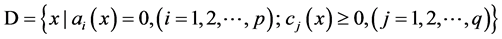 为凸集时,
为凸集时,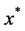 就是上述最优化问题的全局最优解,并且K-K-T条件成为充分必要条件。
就是上述最优化问题的全局最优解,并且K-K-T条件成为充分必要条件。
3. 不允许卖空证券组合投资模型原始–对偶多项式内点算法的计算步骤
不允许卖空证券组合投资模型(1)是一种特殊的非线性规划问题,解决该二次规划问题最初的方法是Wolf算法,可看成是求解线性规划问题单纯型算法的一种推广,但是算法的复杂性是成指数次的。Kozlov M K等 [13] 提出用椭球算法求解二次规划问题,使得算法具有多项式复杂性,但是其理论上的优越性并没有真正应用到实际问题中,直到Karmarkar N [14] 发表Karmarkar算法,二次规划在非线性问题中实现了多项式复杂性及实际计算性。而原始-对偶路径算法是求解线性规划、二次规划及互补松弛等问题最有效的算法 [15] 。其基本思想是借助于一个障碍方程求解迭代方向,而最近一类新的求解线性规划问题的内点算法产生,该算法不仅具有理论上的多项式复杂性,而且在解决实际问题中也很有效 [16] - [18] 。我们将Ross C [19] 求解线性规划问题的方法推广到求解不允许卖空证券组合投资模型的二次凸规划问题中。
在不允许卖空证券组合投资模型(1)中,令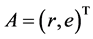 ,
, ,模型(1)转化为如下凸二规划问题(QP)
,模型(1)转化为如下凸二规划问题(QP)
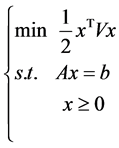
由引理可知,(QP)的对偶规划问题(QD)为

其中协方差矩阵 为正半定矩阵,
为正半定矩阵,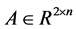 ,
, ,
,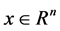 ,
, ,
,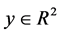 ,
, 。假设(QP)和(QD)满足内点条件,即存在
。假设(QP)和(QD)满足内点条件,即存在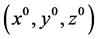 使得
使得
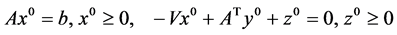 。
。
利用内点法求解(QP)和(QD)的最优解,等价于求解下列参数问题
 (2)
(2)
其中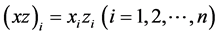 ,
,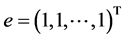 。
。
如果内点条件(IPC)成立,那么对任取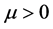 ,方程组(2)有唯一解,记作
,方程组(2)有唯一解,记作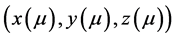 ,称为原始–对偶问题(QP)和(QD)的一个
,称为原始–对偶问题(QP)和(QD)的一个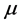 中心。全体
中心。全体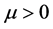 的
的 中心构成(QP)和(QD)的中心路径。当
中心构成(QP)和(QD)的中心路径。当 时,
时,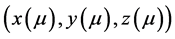 趋于(QP)和(QD)的最优解。利用牛顿法求解方程组(2),即为经典的原始–对偶路径跟踪算法。我们将(2)中的
趋于(QP)和(QD)的最优解。利用牛顿法求解方程组(2),即为经典的原始–对偶路径跟踪算法。我们将(2)中的 用
用 (
(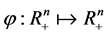 是一一对应函数)来代替,那么(2)转化为如下形式
是一一对应函数)来代替,那么(2)转化为如下形式
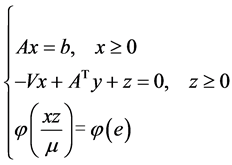 (3)
(3)
应用牛顿法确定牛顿搜索方向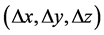 ,将(3)式中的第3个方程线性化,则得到新的迭代方程
,将(3)式中的第3个方程线性化,则得到新的迭代方程
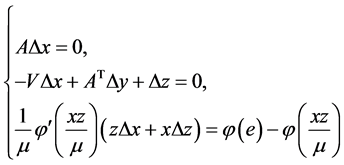 (4)
(4)
作如下投影变换
 ,
,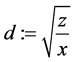 ,
,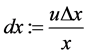 ,
,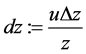 。
。
于是方程(4)转化为
 (5)
(5)
其中 ,
, ;
;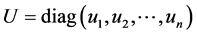 ,
, 。
。
当引入一个函数 时,使得其在
时,使得其在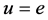 取最小值且
取最小值且 ,则方程(4)转化为
,则方程(4)转化为
 (6)
(6)
由于内点法解线性规划与二次规划问题具有良好的多项式复杂度与稳定性[20] ,取 ,以下给出原始–对偶多项式内点算法求解不允许卖空证券组合投资模型的计算方法。
,以下给出原始–对偶多项式内点算法求解不允许卖空证券组合投资模型的计算方法。
4. 计算实例
考虑6种证券的Markowitz’s证券组合投资模型(文献 [9] ),其收益率方差矩阵为
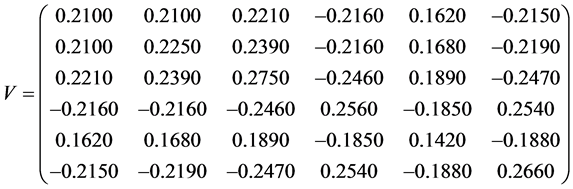 ,
,
6种证券的期望收益率向量为
 ,
,
预期的证券组合收益率为 。
。
取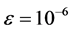 ,
,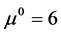 ,
, ,
, ,算法从初始点
,算法从初始点 出发,经过40次迭代到达最优解
出发,经过40次迭代到达最优解 ,对应的证券组合选择模型的最小方差为
,对应的证券组合选择模型的最小方差为 ,为了方便比较,将决策变量的当前值显示到小数点后4位,其它数据显示到小数点后6位。不允许卖空证券组合选择模型的原始–对偶问题多项式内点算法的寻优过程如表1所示。
,为了方便比较,将决策变量的当前值显示到小数点后4位,其它数据显示到小数点后6位。不允许卖空证券组合选择模型的原始–对偶问题多项式内点算法的寻优过程如表1所示。
Table 1. The optimization process for Primal-Dual polynomial interior point method
表1. 原始–对偶问题多项式内点算法的寻优过程
从文献 [9] 的有效集计算方法与本文算法对上例不允许卖空证券组合投资模型分别计算结果中比较可以得知,本文提出的原始–对偶多项式内点算法在计算方面与有效集算法的求解结果是一致的,符合科学
计算方法的设计思路,计算结果可行有效。在求解过程中,若给出的初始点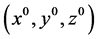 满足
满足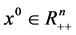 ,
,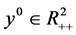 且
且 ,同时
,同时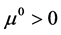 ,使得
,使得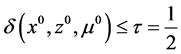 。当
。当 ,
,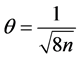 ,则
,则 。当
。当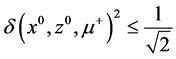 时,经过一次迭代后
时,经过一次迭代后 ,即
,即 ,
,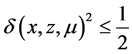 。因此,当
。因此,当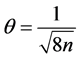 时,算法至多经过
时,算法至多经过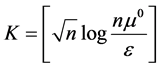 次迭代就可以产生可行解
次迭代就可以产生可行解 ,使得
,使得 。于是该原始–对偶多项式内点算法具有多项式复杂度。
。于是该原始–对偶多项式内点算法具有多项式复杂度。
5. 结束语
本文给出了计算不允许卖空证券组合投资模型的原始–对偶多项式内点算法,理论分析与实例计算表明,该算法由于对偶迭代 的表达式中包含了一些对偶问题的部分信息,可以帮助我们更好更快地对原问题进行改进,计算实验表明原始–对偶多项式内点算法比有效集算法更加有效与稳定,同时该算法可以有多项式时间下得到不允许卖空证券组合投资模型的数值最优解,使整个算法具有较高效率。对于研究制定各种动态证券组合投资和风险控制策略具有一定的理论意义与实用价值。本文的进一步研究将是设计允许卖空条件下证券组合投资模型的内点算法,并分析算法的效率与稳定性。
的表达式中包含了一些对偶问题的部分信息,可以帮助我们更好更快地对原问题进行改进,计算实验表明原始–对偶多项式内点算法比有效集算法更加有效与稳定,同时该算法可以有多项式时间下得到不允许卖空证券组合投资模型的数值最优解,使整个算法具有较高效率。对于研究制定各种动态证券组合投资和风险控制策略具有一定的理论意义与实用价值。本文的进一步研究将是设计允许卖空条件下证券组合投资模型的内点算法,并分析算法的效率与稳定性。
本文中的计算实例算法使用Matlab软件编程实现。
基金项目
本文得到广州中医药大学规划课题(项目号sk0626)和广州中医药大学高等教育教学改革课题(项目号sk1530)的资助。
文章引用
田振明,宋馨雨. 不允许卖空证券组合投资模型的原始–对偶多项式内点算法
A Primal-Dual Polynomial Interior Point Method for Portfolio Investment without Short Sale[J]. 应用数学进展, 2016, 05(01): 51-58. http://dx.doi.org/10.12677/AAM.2016.51008
参考文献 (References)
- 1. Markowitz, H. (1952) Portfolio Selection. Journal of Finance, 7, 77-91. http://dx.doi.org/10.1111/j.1540-6261.1952.tb01525.x
- 2. Markowitz, H. (1959) Portfolio Selection: Efficient Diversification of Investment. Besil Black-Well, Cambridge, 320- 335.
- 3. Ross, S.A. (1977) The Capital Asset Pricing Model, Short Sale Restriction and Related Issue. Journal of Finance, 32, 177-183. http://dx.doi.org/10.1111/j.1540-6261.1977.tb03251.x
- 4. Voros, J. (1987) The Explicit Derivation of the Port-folio Frontier in the Case of Degeneracy and General Singularity. EJOR, 36, 302-311.
- 5. Dybvig, H. (1984) Short Sales Restriction and Kinds on the Mean-Variance Frontier. Journal of Finance, 39, 239-244. http://dx.doi.org/10.1111/j.1540-6261.1984.tb03871.x
- 6. 史树中, 杨杰. 证券组合选择的有效子集[J]. 应用数学学报, 2002, 25(1): 176-186.
- 7. 史树中, 杨杰. 不允许卖空证券组合选择的有效子集[J]. 应用数学学报, 2003, 26(2): 286-299.
- 8. 田振明. 奇异方差矩阵的Markowitz’s证券组合投资决策模型的最优化解法[J]. 数量经济技术经济研究, 2005, 22(10): 135-141.
- 9. 田振明. 有效集法在确定Markowitz’s证券组合投资模型权系数中的应用[J]. 经济数学, 2007, 24(3): 239-243.
- 10. 田振明. 不确定条件下具有容差项的Markowitz’s证券组合投资模型的最优化解法[J]. 数学理论与应用, 2013, 33(3): 48-56.
- 11. 叶中行, 林建忠. 数理金融–资产定价与金融决策理论[M]. 北京: 科学出版社, 1998.
- 12. Antoniou, A. and Lu, W.-S. (2007) Practical Optimization: Algorithm and Engineering Applications. Springer, New York.
- 13. Kozlov, M.K. and Khachiyan, L.G. (1979) Polynomial Solvability of Convex Quadratic Programming. Soviet Mathematics Doklady, 20, 1108-1111.
- 14. Karmarkar, N.K. (1984) A New Polynomial-Time Algorithm for Linear Programming. Combinatorica, 4, 373-395. http://dx.doi.org/10.1007/BF02579150
- 15. Ye, Y.Y. (1997) Interior-Point Algorithm Theory and Analysis. John Wiley and Sons, New York. http://dx.doi.org/10.1002/9781118032701
- 16. Alizudeh, F. and Goldfarb, D. (2003) Second-Order Cone Pro-gramming. Mathematical Programming, 95, 3-15. http://dx.doi.org/10.1007/s10107-002-0339-5
- 17. Bai, Y.Q., Eighamiand, M. and Roos, C. (2003) A New Effi-cient Large-Update Primal-Dual Interior-Point Method Based on a Finite Barrier. SIAM Journal on Optimization, 13, 766-782. http://dx.doi.org/10.1137/S1052623401398132
- 18. Darvay (2002) A New Algorithm for Solving Self-Dual Linear Programming Problems. Studia Universitatis Babes- Bolyai, Seris Information, 47, 15-26.
- 19. Roos, C. (2006) A Full-Newton Step o(n) Infeasible Interior-Point Algorithm for Linear Optimization. SIAM Journal on Op-timization, 16, 1110-1136. http://dx.doi.org/10.1137/050623917
- 20. Wright, S.J. (1997) Primal-Dual Inte-rior-Point Method. Society for Industrial and Applied Mathematics, Philadelphia. http://dx.doi.org/10.1137/1.9781611971453
