ABSTRACT

Time series analysis method is one of the important tools in the field of power load forecasting. It mainly describes the law of the historical data dynamic change over time to predict the future value by establishing a relevant model. In this paper, Winter’s exponential smoothing method and seasonal ARIMA model are applied to model estimating on the power load data, and the authors use the Mean Absolute Percentage Error (MAPE) to measure the accuracy. The results prove that both of them have high fitting and forecasting precision.

Keywords:Electric Load, ARIMA, Time Series, Forecasting, Exponential Smoothing

基于时间序列的电力负荷数据分析

袁硕，陈礼定，孙国鹏，林金官^*

东南大学数学系，江苏 南京

收稿日期：2016年4月23日；录用日期：2016年5月10日；发布日期：2016年5月13日

摘 要

时间序列分析方法是电力负荷预测领域的重要工具之一，它主要通过建立相关模型描述历史数据随时间动态变化的规律以预测未来的值。本文采用温特线性与指数平滑法和季节乘积ARIMA模型对电力负荷实测数据进行建模，然后分别使用平均相对误差MAPE衡量预测精度。研究结果表明：两种方法均有较高的拟合与预测精度。

关键词 :电力负荷，ARIMA，时间序列，预测，指数平滑

1. 引言

电力负荷预测是能量管理系统的重要组成部分，作为电力行业中的一个热点问题一直倍受关注，已经成为实现电力系统管理现代化的重要内容之一。电力负荷预测是根据电力负荷的历史数据及其相关因素，分析负荷的变化规律，综合考虑影响负荷变化的因素，在某些要求下，使用合适的预测模型和方法，以未来的经济形势、社会发展、气候条件等因素为依据，预测估计未来某时段电力负荷数据的过程。电力负荷可以指安装在企业、小区等用户的各种需要用电的设备，也可用以描述用电设备所消耗的电力电量的数值。电力负荷预测是以电力负荷为研究对象所进行的一系列预测工作，电力负荷预测包括对未来电力需求量和用电量的预测，其主要目标是预测未来不同时间和空间上的电力负荷，将预测结果加以分析和应用，以便在未来时刻可以合理地规划和调度电力负荷，既不产生短缺也不造成浪费。

电力市场的不断改革深入使得负荷预测的重要性凸显，各电力公司对电力负荷预测精度的要求也越来越高。传统的预测方法已经比较成熟，预测结果具有一定的参考价值。由于影响因素的不确定性以及负荷数据的复杂性和随机性的存在，负荷的预测总会存在偏差。为了进一步提高电荷预测的精度，就需要在已有的预测方法基础上进行适当的改进和创新。而且随着现代科学技术和学术理论的不断进步，学科交叉日益频繁，理论研究逐步深入，以灰色预测理论、专家系统理论、神经网络等为代表的新兴交叉学科理论的出现，也为负荷预测的快速发展提供了强大的理论基础。

电力系统负荷预测按时间不同可分为长期、中期、短期和超短期负荷预测四种。研究方法也有很多，如回归预测法、趋势外推法、时间序列法、神经网络方法、专家预测法 [1] 等。如果选择预测模型的标准是追求预测精度的极大化，则最好选择时间序列模型。

用时间序列方法预测电力负荷的基本思想是：收集大量准确地历史数据，根据未来与过去时间序列所具有的相似性，通过历史负荷数据揭示其随时间变化的规律，采用简单有效的算法，建立科学的模型，进行大量的检验从而不断完善模型，最终得到最佳的预测结果。描述时间序列数据的变化规律和行为，模型中是允许包含趋势变动、季节变动和随机波动等综合因素影响的。

在实际情况中，绝大部分序列都是非平稳的，因而对非平稳序列的分析更具有普适性，Gramer定理说明：任何一个序列的波动都可以视为同时受到了确定性影响和随机性影响的共同作用 [2] 。一般来讲，非平稳时间序列的分析方法分为确定性时间序列分析(季节模型、趋势模型、移动平均、指数平滑等)和随机性时间序列分析(Box-Jenkins方法、ARCH模型、门限自回归模型等) [3] 。确定性因素分解方法只能提取显著的确定信息，忽略了随机性信息，随机性分析方法的出现弥补了确定性分解方法的不足。

社会经济现象始终存在着不确定性，无论预测方法的使用是否得当，预测模型对历史数据的拟合程度多高，观察值与预测值之间仍会存在偏差。尽量使得误差降到最低是设计方案、研究预测方法的一项重要任务。在进行预测之后我们要利用一些度量指标来评价预测的精度，通常这些度量都是用于事后预测。

2. 模型介绍

2.1. 温特线性与季节指数平滑法

温特方法有三个基础公式和一个预测方程组成 [4] [5] ，每个平滑公式都含有一个平滑系数，这些公式的推导过程在此不详述，只对每个公式的意义做适当的阐述，以便更好地理解和应用。

总体平滑公式：

趋势平滑公式：

季节的平滑公式：

预测方程：

式中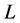，是季节性的长度，如1年的月数、季度数、一周的天数。是季节性的修正系数，即季节指数，这个指数等于时间序列的原始数据与时间序列的一次指数平滑数的比值。由于时间序列的原始数据里包含了季节性、趋势性和随机性，而一次指数平滑数仅包含随机性和倾向性，不包含季节性。为了使中的随机性得到平滑，在季节指数I的方程中，给出新的季节性系数加权；给相当于同一季节，距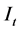最近的季节指数加权。

在的方程中，通过给增量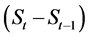加权，给以前的趋势值加权，达到使得时间序列的趋势性平滑的目的。

2.2. ARIMA模型

2.2.1. ARMA模型

自回归移动平均模型(Auto-Regressive Moving Average Model)表示观测值不仅与前p个时刻的自身观测值有关，还与其过去q个随机误差存在一定的依存关系。记ARMA(p,q)模型为：

2.2.2. 求和ARIMA模型

在实际情况中，大多数待处理的数据往往是非平稳的。有些序列存在周期性，例如对于季度或月度数据，就需要消除年周期，则需做周期为4或12的季节差分，以消除季节性；有些序列有明显的上升或下降的趋势，则序列显然是非平稳的，一般也需要通过差分使得数据变平稳；有时存在单位根，也需要进行差分。总之，若是一个ARMA(p,q)的序列，则称是ARIMA(p,d,q)序列，其满足的模型结构可记为：

2.2.3. 季节乘积ARIMA模型

针对具有季节性的时间序列，周期记为s，可以将每个周期段内的同一时刻点位置的数据单独看成一个时间序列，总共可以产生s个子序列。若每个子序列都可以用ARMA(p,q)模型拟合，则有以下模型：

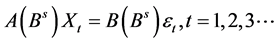(1)

其中不可假设为白噪声序列，因为不能否认各子列之间的相关性。但是在每个子列里面可以假设为白噪声，为了解决这个问题，可以对拟合ARMA(p,q)模型：

(2)

其中，为白噪声，(1)和(2)整合可得模型：

这就是季节乘积模型。

特别地，若每一个子列需要经过差分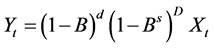，之后才能建立ARMA模型，故模型公式变成：

该模型称为季节乘积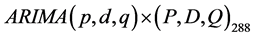模型。

3. 电力负荷数据案例分析

本文采用江苏省南京市新街口金鹰国际购物中心某层用电功率的实测数据(单位：兆瓦)作为电力负荷建模预测的原始数据，该数据由南京市供电局提供，时间区间为从2013年5月1日到5月11日，为每间隔5 min电脑采样一次所得，每天观测288次，总共3168个数据样本。

先使用SAS9.2软件画出原始数据的折线图如图1所示。以2013年5月1日~2013年5月10日的原始数据进行建模分析，不妨设为序列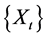，并将2013年5月11日的实际数据用以检验模型的预测精度。

3.1. 基于温特线性与季节性指数平滑法的探究性分析

(1) 模型初值的确定

对于时间序列，使用温特线性与季节性指数平滑法时，基本公式中的一次指数平滑数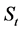的初值为

式中为季节长度。

季节指数初始值为

式中为不同周期同一时刻的平均值，为总体平均值。

的初始值为

图1. 2013年5月1日至11日电力负荷原始折线图

(2) 最优平滑系数的确定

确定最优的准则是使预测值与实际值的均方误差MSE最小。基于这一准则，采用逐个试验法选取平滑系数，即考虑这三个系数的所有可能组合，从中选取MSE最小的组合值。本文通过MATLAB编程以为区间，步长为0.01进行反复计算，并自动选择样本均方误差MSE最小的组合作为最佳预测模型的平滑系数 [4] 。最终得到最优平滑系数，。

(3) 预测与讨论

对于该温特线性与指数平滑模型，计算其绝对误差为0.00000493~0.052688(MW)。95%的数据点的相对误差为0.006~17.2(%)，发现样本数据的拟合效果较好，可以用于预测分析。

进一步，使用该模型对5月11日的电力负荷值进行预测，模型的MAPE = 7.4873 < 10，因此可以认为其预测精度较高。

3.2. 基于ARMA模型的探究性分析

观察原始数据及折线图的变化趋势，可以认为该序列没有缺失值和异常值，且数据围绕一条水平线上下波动，初步判断为平稳序列，但发现原始序列具有明显的季节性特征，其自相关系数呈现出围绕零轴正弦波动的现象，这也说明序列具有周期性。

考虑对原数据先进行季节差分(季节周期为288)，季节差分后的序列记为，其折线图及部分自相关系数如图2和表1所示。自相关系数迅速衰减为零，在滞后288处再次出现显著大于零的值，偏自相关系数具有截尾的特征。通过Ljung-Box统计量来检验序列是否为白噪声序列 [6] ，P值均小于0.05，序列显然是非白噪声的。

对序列采用ADF统计量检验是否含有单位根 [7] ，显然由表2中P值都小于0.05，认为序列不存在单位根，所以平稳，故可以继续以ARMA模型进行拟合。

图2. 前十天季节差分后的折线图

表1. 季节差分后的自相关图

表2. 单位根检验结果

进一步，我们对ARMA(p,q)进行模型定阶，采用最小信息量准则 [6] - [10] (AIC和BIC)选择模型，令p = (0,6)，q = (0,6)，分别计算BIC的值，选择BIC最小(−8.52573)的ARMA(1,1)模型。

下面对进行ARMA(1,1)拟合，采用条件最小二乘法 [6] [8] 进行参数估计及参数显著性检验的P值见表3。

由于常数项显著为零，故拟合无常数项的ARMA(1,1)模型，参数估计如表4所示。

我们可以得到拟合模型公式如下：

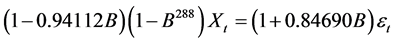
为了检验该模型是否适合于原序列，采用Ljung-Box统计量 [6] 对残差进行白噪声检验，从表5的检验结果看出，延迟6、12期的LB检验的P值均大于0.05，故接受残差为白噪声的原假设，认为在0.05显著性水平下，残差序列显著为白噪声，故可以认为残差序列之间不存在显著的自相关性，原序列中的相关信息已经被充分提取出来，这说明模型适合于该序列(AIC = −14761.3，SBC = −14749.6)。

最后，利用前面建立的差分后最佳ARMA模型，我们可以得到前十天的拟合值，将它们与真实值进行比较，可以发现只有极少数点处于95%置信区间外，该模型拟合的绝对误差为0.00003~0.06377(MW)，95%的数据点的相对误差为0.02~25.7(%)，可以认为，该模型的拟合能力较好，可以用于预测。

进一步，使用该模型预测5月11日的电力负荷值，然后对比11日的预测值与真实值，计算其平均相对误差为MAPE = 10.5925，由于其预测的平均相对误差值大于10，所以认为以上分析模型的预测效果不够理想。试图将以上分析作为铺垫性分析，猜想这可能是趋势性的存在所导致的，进一步，继续采用季节乘积ARIMA模型进行建模。

3.3. 基于乘积季节ARIMA模型的探究性分析

前面已经发现序列具有明显的季节性(季节周期为288)，其趋势性无法判断，已经分析了只进行季节

表3. ARMA(1,1)参数估计及检验结果

表4. 无常数模型参数估计

表5. 残差检验

差分的情况，现对原序列进行一阶差分再做288步季节差分，希望能消除季节效应和趋势效应，差分后的序列记作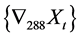，为了进一步检验序列的平稳性，采用ADF单位根检验，检验结果显示序列不存在单位根，见表6。

接下来进行模型的定阶，考察差分后的ACF和PACF图的性质，见表7。自相关图显示只有滞后一阶时超出了2倍标准差范围，可以判断为1阶截尾的，而偏自相关系数下降较缓慢，初步判断为MA(1)模型 [6] [7] [9] ，我们尝试拟合季节乘积ARIMA模型 [11] [12] ，模型拟合的AIC、SBC及残差白噪声检验结果见表8。

从表中看出的AIC和SBC均最小，所以选择该模型为最佳的拟合模型采用条件最小二乘法得到参数估计的值及参数显著性t检验结果如表9。剔除掉常数项后重新拟合结果见表10。

因此，对该电力负荷序列的拟合模型公式为：

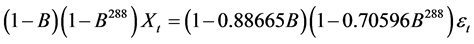
采用已得的最佳季节乘积ARIMA模型对5月1日至10日的数据进行拟合，其绝对误差为0~0.06446(MW)，95%的数据点的相对误差为0~20.6(%)，对比来看，其拟合的效果要比前面铺垫分析模型要好一些，因此可以用于预测。

进一步，使用该模型对5月11日的电力负荷值进行预测。再计算该模型的MAPE = 7.4897 < 10，因此，该模型的预测精度显然比前一模型要高，可以认为该模型是合理的。

表6. ADF检验

表7. 季节差分后自相关图

表8. 比较各季节乘积模型

表9. 参数估计

表10. 无常数参数估计

4. 结论

预测精度是衡量预测方法是否适用于预测对象的一个重要指标。无论一个模型的拟合精度是否够高，作为预测模型仍然需要比较预测精度，衡量预测精度的指标有很多(RMSE、MAE、MAPE [3] [11] 等)，本文采用的预测精度为平均相对误差：

如果MAPE越小，说明模型的预测精度越高。若MAPE < 10，说明模型的预测结果比较好。

根据以上三个模型的分析来看，实际上，第二个分析模型可以看作是季节乘积ARIMA模型的特例。所以三个模型分别为：温特线性与指数平滑模型、、。它们的MAPE分别为：7.4873、10.5925、7.4897。所以温特线性与指数平滑模型的预测能力较强。

因此，使用温特线性与指数平滑法对2013年5月11日的电力负荷进行预测，效果最好，其预测图与真实值的对比图见图3和图4两幅图(x：预测值，y：真实值，为显示对比效果，分割成两幅放大图)，可以看出预测是近乎合理的，从图上看出，虽然采用温特线性与指数平滑法得到的2013年5月11日电

图3. 5月11日的电力负荷预测值与真实值对比图

图4. 5月11日的电力负荷预测值与真实值对比图

力负荷的预测值数据与实际观测数据有略微的偏差，但是其MAPE的值(7.4873)较小，所以本文认为可以将温特线性与指数平滑法用于该样本数据的实际预测。

再次从预测图看，前段数据图为深夜时分，用电量较低，图线走势比较平稳，预测的偏差显然较小；而后段中出现了比较大的波动，这很有可能是由于白天用电较多，各种商场大型设备的启用使得商场用电功率产生不规则的波动，图中整天的预测折线明显处于实测值的靠下方，这表明预测值要比实测值偏小一些。在一定意义上，这可以说明温特线性与指数平滑法预测过程中对趋势性的处理需要进一步改进，我们猜测原因可能是：一方面，该方法的线性处理并不完全适合于本文所采用的样本数据；另一方面，短期内外界因素导致的波动所产生的异常数据对模型趋势造成了影响 [13] 。温特线性与指数平滑法有着操作简单，精确度高的优点，该方法在今后的一般线性预测中将会发挥很重要的作用，但它所暴露的缺点更需要进一步完善。

基金项目

国家自然科学基金(11571073)、江苏省自然科学基金(BK20141326)和教育部博士点基金(2012009211 0021)资助。

文章引用

袁硕,陈礼定,孙国鹏,林金官. 基于时间序列的电力负荷数据分析
Analysis of Electric Load Data Based on Time Series[J]. 应用数学进展, 2016, 05(02): 214-224. http://dx.doi.org/10.12677/AAM.2016.52028

参考文献 (References)