Advances in Applied Mathematics
Vol.05 No.04(2016), Article ID:18978,9
pages
10.12677/AAM.2016.54073
Quadratic Normal Forms and Universal Unfoldings of Three-Dimensional Systems with Nilpotent Singular Points
Dandan Xie1,2, Nana Zhang1,2
1School of Mathematics and Statistics, Shandong Normal University, Jinan Shandong
2School of Science, Linyi University, Linyi Shandong

Received: Oct. 26th, 2016; accepted: Nov. 8th, 2016; published: Nov. 18th, 2016
Copyright © 2016 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
In this paper, for three-dimensional dynamic systems, we discuss and analyze three classes of equations which have nilpotent singular points. The normal forms of quadratic polynomials are obtained by normal formal theory. Then, the universal unfoldings are obtained by using coordinate translation.
Keywords:Three-Dimensional System, Nilpotent Singular Point, Quadratic Polynomial, Normal Form, Universal Unfolding

具有幂零奇点三维系统的二次规范型 及普适开折
谢旦旦1,2,张娜娜1,2
1山东师范大学数学与统计学院,山东 济南
2临沂大学理学院,山东 临沂

收稿日期:2016年10月26日;录用日期:2016年11月8日;发布日期:2016年11月18日

摘 要
本文对三维动力系统中三类具有幂零奇点的微分方程进行了讨论和分析,通过规范型理论得出了含有二次多项式的规范型,再利用坐标平移得出了它们的普适开折。
关键词 :三维系统,幂零奇点,二次多项式,规范型,普适开折

1. 引言
规范型理论是通过一系列的近恒同非线性变换化简原有的微分方程,得到奇点附近非线性项的简单形式,其实质是消去起次要作用的非线性项,而且简化后的系统与原系统拓扑等价。规范型理论在提出以后很长一段时间并未得到较快的发展,主要是由于计算量大且计算过程比较复杂。在罗定军等人的著作 [1] 中,对于规范型进行了详细的研究。近几十年来,国内外学者对于规范型理论进行了许多卓有成效的研究,到目前为止,已经提出了可用于规范型的计算矩阵表示法、共轭算子法、李代数表示论法、多重李括号法、多尺度摄动法、谐波平衡法等多种方法。
近年来,许多学者利用MAPLE等计算机软件程序计算出了一些高维非线性系统的规范型,但他们都是在原有的基本理论上,利用计算机进行迭代计算,本文主要利用最基本的规范型理论,利用李代数方法对三维系统中可能出现的情况进行一一分析,并求出他们的规范型形式。
2. 规范型的基本理论
考虑系统
 , (2.1)
, (2.1)
其中 为标准型矩阵,
为标准型矩阵, ,
,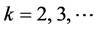 ,
, 表示
表示 的
的 元
元 次齐次多项式所组成的空间。作变换
次齐次多项式所组成的空间。作变换
 , (2.2)
, (2.2)
其中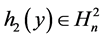 ,目标是选取适当的
,目标是选取适当的 使(2.1)的二次项尽可能地简化。
使(2.1)的二次项尽可能地简化。
由(2.2)得: ,故
,故
 。
。
从而
 , (2.3)
, (2.3)
其中 表示
表示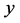 的三次齐次项,
的三次齐次项,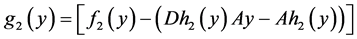 。
。
引入关于 的伴随算子
的伴随算子 ,
, ,则(2.3)可表为
,则(2.3)可表为
 。 (2.4)
。 (2.4)
设算子 在
在 中的值域为
中的值域为 ,将
,将 表为
表为 及其补空间
及其补空间 的直和
的直和 。
。
对于(2.1)中的二次项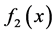 ,有以下两种情况:
,有以下两种情况:
1) 如果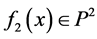 ,则存在
,则存在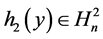 ,使
,使 。这时(2.4)中不再出现二次项。
。这时(2.4)中不再出现二次项。
2) 如果 ,则对适当的
,则对适当的 ,
, ,
, ,因此可按
,因此可按 中的基底
中的基底
去讨论变换后方程(2.4)中的二次项所可能出现的各种形式。连同线性项在内,把方程(2.3)截止到二次项,所得系统 称为原系统的二次规范型。
称为原系统的二次规范型。
类似地,对三次项可依同样的过程讨论。设取变换 ,其中
,其中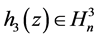 。这一变换不会影响到一次和二次项,故(2.3)化为
。这一变换不会影响到一次和二次项,故(2.3)化为
 , (2.5)
, (2.5)
其中 ,
,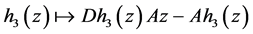 。同样考虑
。同样考虑 在
在 中的值域
中的值域 以及它在
以及它在 中的补空间
中的补空间 。当
。当 时,变换后的系统将不含三次项,否则可取适当的
时,变换后的系统将不含三次项,否则可取适当的 ,使系统化为
,使系统化为
 。 (2.6)
。 (2.6)
在(2.6)中,截断到 为止的方程就称为三次规范型,可依
为止的方程就称为三次规范型,可依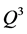 中的基底得出它的形式。重复此步骤可进一步确定4次,5次,……规范型。当然,次数越高,形式将越复杂。如果系统(2.1)为解析,则上述步骤可无限地进行下去,可形式地得到幂级数式的规范型。因而需讨论它是否收敛 [1] [2] 。
中的基底得出它的形式。重复此步骤可进一步确定4次,5次,……规范型。当然,次数越高,形式将越复杂。如果系统(2.1)为解析,则上述步骤可无限地进行下去,可形式地得到幂级数式的规范型。因而需讨论它是否收敛 [1] [2] 。
注:在研究系统的第 次规范型时,它与前
次规范型时,它与前 次无影响。且规范型的表示不是唯一的,它依赖于补空间中基底的选择。
次无影响。且规范型的表示不是唯一的,它依赖于补空间中基底的选择。
3. 具有幂零奇点三维系统的二次规范型及普适开折
考虑三维系统
 , (3.1)
, (3.1)
其中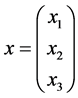 ,
, ,现求它的二次规范型以及它的普适开折。
,现求它的二次规范型以及它的普适开折。
因 三分量各有六个任意系数,故
三分量各有六个任意系数,故 等同于一个
等同于一个 ,在其中可取如下一组基底:
,在其中可取如下一组基底:
 ,
, ,
, ,
, ,
, ,
, ,
, ,
,
 ,
, ,
, ,
,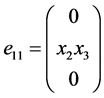 ,
, ,
, ,
, ,
,
 ,
, ,
, ,
, 。
。
因零点是幂零奇点,所以 总可以化成以下几种形式:
总可以化成以下几种形式:
 ,
, ,
, ,
, ,
, ,
, 。
。
而当 时,可以经过
时,可以经过 ,
, ,
,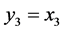 变成
变成 。
。
而当 时,可以经过
时,可以经过 ,
,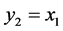 ,
, 变成
变成 。
。
而当 时,可以经过
时,可以经过 ,
, ,
, 变成
变成 。
。
所以,下面我们只讨论 ,
, ,
, 三种情况。
三种情况。
3.1. 情况一
由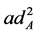 ,
,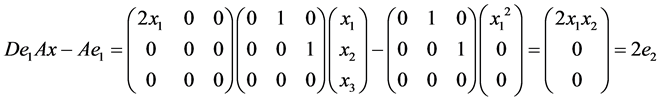 。
。
同样的, ,
, ,
, ,
, ,
, ,
,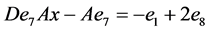 ,
, ,
, ,
, ,
, ,
,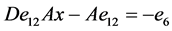 ,
, ,
,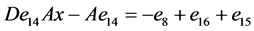 ,
,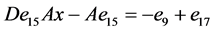 ,
, ,
,
 ,
, 。
。
即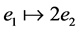 ,
, ,
, ,
, ,
, ,
, ,
, ,
,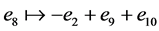 ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, 。
。
于是算子 相对于
相对于 的这组基底的矩阵为
的这组基底的矩阵为
 。
。
它的秩等于14,故 的值域为
的值域为 ,取
,取 ,
, ,
, ,
, ,
, ,
, ,
,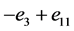 ,
, ,
, ,
, ,
, ,
,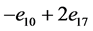 ,
, ,
, 。
。 的补空间可取为
的补空间可取为 。于是得到系统的一个二次规范型为
。于是得到系统的一个二次规范型为
 ,
,
即
 。 (3.2)
。 (3.2)
结论3.1.1:在情况一中,(3.1)的一个二次规范型为(3.2)。
对(3.2)加扰动后 [1] [3] ,它为 。
。
再对 ,
,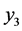 移动坐标 [4] ,令
移动坐标 [4] ,令 ,
,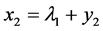 ,
, ,得
,得
 。 (3.3)
。 (3.3)
结论3.1.2:(3.2)的一个普适开折为(3.3)。
因(3.1)的一个二次规范型为(3.2),所以系统(3.1)拓扑等价与(3.2)。而(3.2)的一个普适开折为(3.3),所以(3.1)拓扑等价系统的一个普适开折为(3.3)。
结论3.1.3:(3.1)拓扑等价系统的一个普适开折为(3.3)。
3.2. 情况二
由 ,
, 。
。
类似的,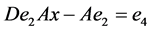 ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
,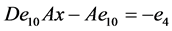 ,
, ,
, ,
, ,
,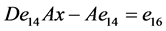 ,
,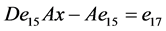 ,
, ,
, ,
, 。
。
于是算子 相对于
相对于 的这组基底的矩阵为
的这组基底的矩阵为
 。
。
它的秩等于10,故 的值域为
的值域为 ,取
,取 ,
, ,
, ,
, ,
, ,
,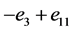 ,
,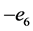 ,
, ,
, ,
,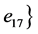 ,其补空间可取为
,其补空间可取为 。相应地,系统的一个二次规范型为
。相应地,系统的一个二次规范型为
 。
。
亦即
 , (3.4)
, (3.4)
结论3.2.1:在情况二中,(3.1)的一个二次规范型为(3.4)。
对(3.4)加扰动后 [1] [3] ,它为
 。
。
再对 移动坐标 [4] ,令
移动坐标 [4] ,令 ,
,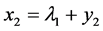 ,
, ,得
,得
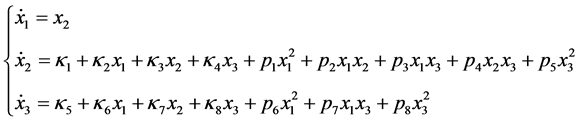 。 (3.5)
。 (3.5)
结论3.2.2:(3.4)的一个普适开折为(3.5)。
结论3.2.3:(3.1)拓扑等价系统的一个普适开折为(3.5)。
3.3. 情况三
由 ,
, 。
。
类似的, ,
, ,
,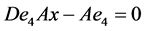 ,
,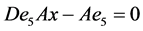 ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
,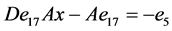 ,
, 。
。
于是算子 相对于
相对于 的这组基底的矩阵为
的这组基底的矩阵为
 。
。
它的秩等于10,故 的值域为
的值域为 ,取
,取 ,
, ,
, ,
, ,
, ,
, ,
,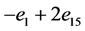 ,
,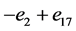 ,
, ,
, ,它的补空间取为
,它的补空间取为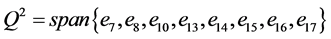 。相应地,系统的一个二次规范型为
。相应地,系统的一个二次规范型为
 。
。
亦即
 ,(3.6)
,(3.6)
结论3.3.1:在情况三中,(3.1)的一个二次规范型为(3.6)。
对(3.6)加扰动后 [1] [3] ,它为
 。
。
再对 移动坐标 [4] ,令
移动坐标 [4] ,令 ,
, ,
, ,得
,得
 。 (3.7)
。 (3.7)
结论3.3.2:(3.6)的一个普适开折为(3.7)。
结论3.3.3:(3.1)拓扑等价系统的一个普适开折为(3.7)。
致谢
本文是在金银来老师的指导下完成的,借此向金老师致以深深的敬意和衷心地感谢!
基金项目
国家自然科学基金(11601212)、山东省自然科学基金(ZR2015AL005)和山东省高等学校科技计划(J16LI03)资助。
文章引用
谢旦旦,张娜娜. 具有幂零奇点三维系统的二次规范型及普适开折
Quadratic Normal Forms and Universal Unfoldings of Three-Dimensional Systems with Nilpotent Singular Points[J]. 应用数学进展, 2016, 05(04): 630-638. http://dx.doi.org/10.12677/AAM.2016.54073
参考文献 (References)