中国海洋大学食堂菜谱的优化模型研究 Study on Mathematical Model of the Optimization of the Menu of OUC

doi:10.12677/AAM.2018.72024

Advances in Applied Mathematics
Vol.07 No.02(2018), Article ID:23869,11 pages
10.12677/AAM.2018.72024

Study on Mathematical Model of the Optimization of the Menu of OUC

Jian Huang, Wangning Gao, Xiangdong Xie, Wenxuan Han, Zhihang Wang, Xiang Gao^*

●How to Cite this Article

School of Mathematical Sciences, Ocean University of China, Qingdao Shandong

Received: Feb. 7^th, 2018; accepted: Feb. 21^st, 2018; published: Feb. 27^th, 2018

ABSTRACT

By using price and satisfactions of student we make a double objective integer linear programming model. At the last we add a fuzzy evaluation system to the model. This menu optimization model can solve nutritional intake problem and the problem of the waste of leftovers.

Keywords:Menu Optimization, Double Objective Linear Programming, Fuzzy Evaluation, MATLAB

中国海洋大学食堂菜谱的优化模型研究

黄健，高望宁，谢向东，韩文煊，王志航，高翔^*

中国海洋大学数学科学学院，山东青岛

收稿日期：2018年2月7日；录用日期：2018年2月21日；发布日期：2018年2月27日

摘要

我们通过价格和满意度的双目标整数线性规划模型，再加上模糊评价体系，建立了优化菜谱模型，通过此模型可以解决食堂菜品制作数量不合适导致的营养摄取问题和剩菜过多的浪费问题。

关键词 :菜谱优化，双目标整数规划，模糊评价，MATLAB

This work is licensed under the Creative Commons Attribution International License (CC BY).

http://creativecommons.org/licenses/by/4.0/

1. 引言

通过查阅相关资料 [1] ，我们了解到有关食堂就餐问题的很多方面，如排队问题、成本问题、师生满意度问题等，由此我们受到启发，决定以食堂的某一打饭窗口为例建立我们的食堂菜谱优化模型。首先，我们询问了食堂的厨师、经理，从大体上把握了饭菜的食材比例、价格、消费情况，通过对其的采访，我们了解到了食堂现如今的菜谱模式仍是厨师凭借其经验决定数量的多少，这种方式往往在购买食材时，会产生过溢现象，往往会将剩下的食材留到隔天再进行利用处理，于是我们发现建立一个数学模型来对菜谱的菜量进行计算很有必要！其次，我们调查了师生对食堂饭菜的满意度(即他们就餐时的喜好)，再结合二者，与我们查阅的人体所需营养元素作比较，大体确定我校师生可能缺少的营养元素范围，并以价格最低和满意度最高为双目标建立整数规划模型，旨在为食堂提供一种可行性的菜谱优化方案。结合对同学到该窗口就餐的调查情况，进一步可分析哪些饭菜含大量师生所缺的营养元素且师生不喜欢吃，研究其原因并制定出相应的解决方案，结合食材所含主要营养元素，实现研究问题从定性到定量的转化。

2. 问题的提出

由于食堂工作人员做菜的种类以及每种菜品做多少都是根据以往经验决定的，因此不免出现一些某些菜做多了或少了的现象，无意识中造成食物浪费或师生营养不良，为此我们将数学运用于实践，通过数学建模为广大师生提供合理的就餐建议，可做到平衡营养、口味和价格，让大多数人吃的满意，有助于提高同学们对于学校的认可度以及归属感，同时还可减少食堂不必要的浪费，增加到食堂就餐的人数，提高食堂的收益。基于这两个主要目的，我们建立了基于双目标整数规划的“食堂菜谱”优化模型。

3. 问题的分析

通过走访调查，我们发现食堂的工作人员做菜时缺乏一种衡量机制，大多数人是凭经验决定做菜的种类以及每种菜品做多少，因此难免会出现一些问题。而食堂各类窗口菜品种类又不尽相同，无法进行统一评价。为解决这一难题，我们决定化整为零，以一个打饭窗口为例，建立菜谱优化模型，给出合理化建议，使在该窗口打饭的师生既满足于菜的口味、又能获得日常所需的营养，同时还能减少花销。因为很多同学会因为食堂菜品口味不佳、价格太贵而选择不去食堂，通过我们的模型可以解决这方面的一些问题，从而会增加到食堂的就餐人数，间接增加食堂的收入。

通过查阅资料，选定九类营养物质为限定条件 [2] 。我们的研究是以一个窗口为例，大概有八九种菜，我们可以设置八个未知数，建立限定条件。我们通过后期模型程序计算可以得出每种菜品中所含的九种营养元素量为多少。以菜品价格最低和菜品满意度最高为目标函数，得出最优的菜品组合。从而建议食堂哪些多做，达到定性分析。

然后建立单位菜品营养元素系数计算模型如“图1所示”。目的是计算100 g菜品中蛋白质等九种元素的分别含量。模型设立：输入菜品名，判定荤素比例，再把荤素分别细分为12小类，然后分别计算所分项目单位kg重量含蛋白质等九种营养元素的质量。如此，我们就求出了一道菜的营养元素系数(营养元素系数的含义：九种营养元素在单位食材中的含量)。代入一开始的限定优化模型中，即可得出最优解 [3] 。

Figure 1. Dishes hierarchy diagram

图1. 菜品层次结构图

通过问卷调查和德尔菲评判法搜集数据并进行汇总、整理和分析得到海大学生对于食堂菜系口味(满意度)和价格的需求。

探访食堂厨师和经理等人了解海大食堂每日的食材的种类，数量以及价格。上网和查阅书籍了解单位食材中含有人体必需营养物质的数量。

搜集素材，并进行整理和了解人体所必须的营养物质的种类以及数量进行数据建模得出平均值，作为后期菜谱研究的限定条件。

以海大学生的口味(满意度)和经济承受能力为主要权重指数，配合食材的处理难度，在满足必需营养物质的情况下进行数据建模，通过层次分析，概率统计，权重分配等多种方法实现菜谱模型的建立。

4. 模型的假设

1) 假设学生一天吃三顿饭、只打4份菜且都在同一窗口打饭，米饭摄入为400 g；

2) 假设每天到窗口A就餐人数是固定的，设为a；

3) 假设窗口A的菜品种类固定，每天所用食材固定，设为b；

4) 假设学生只存在营养不足问题，营养只来源于食材与米饭且不考虑营养过剩的情况；

5) 假设早饭的营养摄入量为一天所需营养的30%。

5. 模型的建立与优化

5.1. 模型的建立

以一个打饭窗口为例，不妨假定每个窗口有n种菜品，经调查，打饭时每份菜的质量约100 g，研究变量的限制条件海大师生人体(体重按65 kg考虑)平均一天所应摄取的(蛋白质)，(脂肪)，(膳食纤维)，(维生素b1)，(维生素b2)，(钙)，(铁)，(锌)的含量，如下文“表1所示”。目标函数为求满足摄入量时各种菜品组合的最小价格及最大满意度，假定每个人一天吃三顿饭，且中晚餐均在同一个窗口打2份菜，即可建立双目标最优化模型如下 [4] ：

目标函数：

$\min z_{1} = a_{1} q_{1} y_{1} + a_{2} q_{2} y_{2} + \dots + a_{n} q_{n} y_{n}$ (1)

$\max z_{2} = a_{1} p_{1} y_{1} + a_{2} p_{2} y_{2} + \dots + a_{n} p_{n} y_{n}$ (2)

Table 1. Daily human nutrition table

表1. 人体每日所需营养物质表

PS: Men and women have different demand for iron and vitamin B1, B2, and take the average 注：铁、维生素b1、b2男女略有差异，这里取其均值

${\begin{array}{l} 75 \times 0.7 - 2.6 \times 4 \leq 4 m x_{1} \\ 50 \times 0.7 - 0.3 \times 4 \leq 4 m x_{2} \\ 30 \times 0.7 - 0.2 \times 4 \leq 4 m x_{3} \\ 1.35 \times 0.7 - 0.02 \times 4 \leq 4 m x_{4} \\ 1.3 \times 0.7 - 0.03 \times 4 \leq 4 m x_{5} \\ 800 \times 0.7 - 7 \times 4 \leq 4 m x_{6} \\ 17.5 \times 0.7 - 2.2 \times 4 \leq 4 m x_{7} \\ 15.5 \times 0.7 - 1.36 \times 4 \leq 4 m x_{8} \\ m = a_{1} y_{1} + a_{2} y_{2} + \dots + a_{n} y_{n} \end{array}$

$y_{n}$ 为菜品的种类

$m$ 为所选菜的总质量

$q_{n}$ 为菜品 $y_{n}$ 的价格

$p_{n}$ 为菜品 $y_{n}$ 的满意度

$a_{n}$ 为一天中打到菜品的次数，其中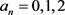

5.2. 模型的优化

在提出上述模型的基础上，我们考虑到单目标的线性规划，并不能将食堂菜谱的情况完全反应出来，于是在4.1模型的基础上，我们引进菜品购买趋势h的概念(食堂菜品价格越贵，顾客购买的趋势越低，食堂菜品满意度越高，顾客购买趋势越高)通过确定海大学生对于价格和口味的选取比重，可以确立菜品购买趋势中价格与满意度的权重。通过大量的问卷调查，我们得到了海大学生对于价格和满意度的权重为21:57。从而构建双目标线性规划方程

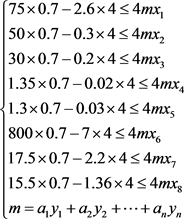
求得满足人体最低营养要求情况下的购买趋势最大的菜品组合

6. 模型的求解

6.1. 窗口菜品营养元素计算

我们通过对食堂经理的采访和网上数据查询得到了窗口A中的八道菜的食材比例，按3. 问题的分析的营养元素计算模型分类如“图1所示”要求可得 [5] ：

杭椒炒肉：猪肉:杭椒 = 3:2，即根茎类:猪肉 = 3:2

炸鸡柳：鸡肉 = 1，即鸡肉 = 1

西红柿炒蛋：鸡蛋:西红柿 = 1:1，即鸡蛋:瓜类 = 1:1

葱花炒蛋：葱:鸡蛋 = 1:2，即鸡蛋：根茎类 = 1:2

炒绿豆芽：豆芽 = 1，即豆类 = 1

酱香鸭肉：鸭肉 = 1，即鸭肉 = 1

土豆炖排骨：土豆:排骨 = 1:1，即根茎类:猪肉 = 1:1

菜花炒肉：菜花:猪肉 = 5:2，即叶类：猪肉 = 5:2

如“表2所示”将上述数据代入营养元素计算模型可得

6.2. 窗口最优菜品组合计算

如“表3所示”

将x₁ = [16.7 6.6 6.42 9.075 2.5 15 7.55 4.822]

x₂ = [35.4 5.65 14.92 7.392 0.2 1.5 18.6 10.801]

x₃ = [0 0.35 0.72 0.3960 2.1 0 0.6 0.639]

x₄ = [0.07 0.165 0.142 0.2409 0.05 0.01 0.155 0.0851]

x₅ = [0.07 0.165 0.082 0.2211 0.17 0.07 0.095 0.0748]

x₆ = [37 231.5 25.8 305.91 29 6 22.5 26.59]

x₇ = [1.7 1.25 1.48 1.98 1.5 4.1 1.5 0.89]

x₈ = [1.1 0.54 0.962 0.7425 0.54 1.17 1.145 1.0305]

代入5.2双目标线性规划方程中的线性规划的约束条件中，求得目标函数最大的情况下a的取值为

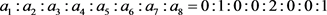
可得最优的菜品组合为西红柿鸡蛋和菜花炒肉各一份，绿豆芽两份。

Table 2. All kinds of nutrient elements in 100 g material

表2. 各类100 g食材所含各类营养元素

Table 3. All kinds of nutrient elements in the menu of window A

表3. 窗口A的菜品所含各类营养元素

6.3. 窗口菜品制作数量计算

在保证食堂窗口菜品丰富度不变的情况下，我们对该窗口菜品的制造数量进行调整，使得该窗口的菜品更加能满足学生的各方面需求。通过一星期实地考察我们得知了该窗口每天中晚接待学生的数量大致成一个稳定的数字270，按之前的假设可得，该窗口需要准备540份菜，我们通过6.2的窗口最优组合计算得到了最优菜品的比例，接下来我们需要确定非最优菜品与最优菜品的比例，加上“表4所示”和“表5所示”可以通过计算最优菜品的平均菜品购买趋势数和非最优菜品的平均菜品数的比例来得到。

炸鸡柳的菜品购买趋势数：2.9

葱花鸡蛋的菜品购买趋势数：3.4

酱香鸭肉的菜品购买趋势数：5.1

土豆排骨的菜品购买趋势数：3.1

西红柿炒蛋的菜品购买趋势数：2.76

菜花炒肉的菜品购买趋势数：3.67

绿豆芽的菜品购买趋势数：3.72

杭椒炒肉的菜品购买趋势数：3.20

所以最优菜品平均购买趋势数:非最优菜品平均购买趋势数 = 3.24:3.56，即炸鸡柳：西红柿鸡蛋：杭椒炒肉:葱花炒蛋:绿豆芽:酱香鸭肉:土豆炖排骨:菜花炒肉 = 3.56:3.24:3.56:3.56:6.48:3.56:3.56:3.24 = 89:81:89:89:162:89:89:81

我们通过对食堂工作人员的采访得知每份菜品的质量为100 g从而得到了每道菜应做的分量为：

炸鸡柳(6.250 kg)

西红柿鸡蛋(5.688 kg)

杭椒炒肉(6.250 kg)

葱花炒蛋(6.250 kg)

绿豆芽(11.376 kg)

酱香鸭肉(6.250 kg)

土豆炖排骨(6.250 kg)

菜花炒肉(5.688 kg)

7. 模型的检验与评价

7.1. 建立模糊综合评价体系

1) 由之前讨论的因素作为菜谱模型合理性的因素集，其中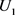表示菜品的价格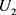，表示菜品的满意度.

2) 建立评价对象的等级集合V

3) 对于菜品价格的评价，V = {合理，一般，不合理}

4) 对于菜品满意度的评价，V = {满意，一般，不满意}

根据第一次的调查问卷，我们可以得到菜品价格评判的范围，由第二次的问卷调查，我们可以得到

Table 4. The price of the dishes in window A (Unit: Yuan)

表4. 窗口A的菜品的价格(单位：元)

Table 5. The satisfaction of the dishes in window A (Range: 1~10)

表5. 窗口A的菜品的满意度(范围：1~10)

菜品满意度评判的范围.故设置区间，对于价格和满意度建立隶属矩阵R，以价格为例，对应的隶属度向量的第一个分量可定义为价格为合理的菜品数一天做的量占该窗口总菜品总数的比例，其他分量以此类推，原菜谱对应的隶属度每种菜品按等量取均值计算。

进而确定各个评价指标的权重W，由之前的问卷调查可以得到权重，设

通过权重系数矩阵W与隶属度矩阵R的模糊变换得到模糊评判集S

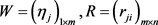
7.2. 对食堂原菜谱建立隶属矩阵

在确定隶属关系时，通常是由专家或与评价问题相关的专业人员根据评判等级对评价对象进行打分，然后统计打分结果，然后可以根据绝对值减数法求得，即

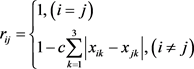
这里取c = 1/1000

7.3. 模型求解计算

价格在合理等级的菜品有：西红柿鸡蛋，葱花炒蛋，绿豆芽，菜花炒肉。由我们对于食堂的采访得知食堂原菜谱做菜比例为1:1:1:1所以这个等级的菜应做540 = 270道。此即为依次类推可得到和。

满意度在合格等级的菜品有：酱鸭肉所以食堂原菜谱中这道菜应做道(菜品制作时不会过多，所以一律舍去)，此即为，依次类推可得到和。

利用

得到食堂原菜谱的隶属矩阵

价格在合理等级的菜品有：西红柿鸡蛋，葱花炒蛋，绿豆芽，菜花炒肉。由食堂新菜谱可知合理等级的菜应做81 + 89 + 162 + 81 = 413道，此即为，依次类推得到和.再由不同满意度级的菜品数，得到，利用7.1.5求隶属向量的方法求出隶属矩阵

7.4. 模糊评判集检验

模糊评判集 (W为价格和满意度的权重系数，R为新旧两菜谱的隶属矩阵)

则原菜谱的模糊评判集为

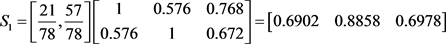
新菜谱的模糊评判集为

由最大隶属矩阵原则可知新菜谱和旧菜谱均属于等级2，即综合评价为一般，为进行精细比较，我们赋予不同等级具体的得分，进行综合得分进一步比较

设等级1得分为8，等级2得分为6，等级3得分为4

则旧菜谱综合得分为：0.6902 × 8 + 0.8858 × 6 + 0.6978 × 4 = 13.6276

则新菜谱综合得分为：0.7428 × 8 + 0.9052 × 6 + 0.7690 × 4 = 14.4496

故知修改后的菜谱比原来的菜谱有所改进。

8. 模型的应用与推广

使用该模型时，选取使用食堂，将该食堂的所有菜品按照顺序排列，厨师先将菜品的材料按照模型2中的12种食材类别分类，并将菜品各食材的比例表示出，(如西红柿鸡蛋，其食材比例为鸡蛋:西红柿 = 1:1，则其表示为[0 0 0 0 0 0 0 0 0 0.5 0 0.5]代表一道菜品鸡蛋和西红柿各占0.5，其余种类食材质量为0)将各菜品用上述表示法输入单位菜品营养元素系数计算模型中，得到每100 g该菜品中蛋白质等九种元素的分别含量。得到所有菜品的营养元素含量后，将其代入模型4.2中即可得到最优菜品组合，该食堂对其所有菜品进行调查如在食堂挂上意见本让学生打分，得到每道菜品的满意度之后，利用购买趋势数计算程序算出每道菜品的购买趋势数。再计算出最优菜品组合的购买倾向平均数和非最优菜品的购买倾向平均数，通过之间的比值确定出非最优菜品的制造数量，再根据最优菜品之间的比例，确定几种最优菜品各自的制造数量，最终得到该食堂所有菜品的制造数量。

资助信息

山东省研究生教育创新计划项目“一线贯通式几何方向研究生课程群及信息化平台建设”(SDYY15129)，山东省研究生导师指导能力提升项目“布尔巴基观点下的几何与代数方向研究生课程体系与课程群建设”(SDYY17009)。

文章引用

黄健,高望宁,谢向东,韩文煊,王志航,高翔. 中国海洋大学食堂菜谱的优化模型研究
Study on Mathematical Model of the Optimization of the Menu of OUC[J]. 应用数学进展, 2018, 07(02): 195-205. http://dx.doi.org/10.12677/AAM.2018.72024

参考文献 (References)

1. 胡敏. 新编营养师手册(第三版) [M]. 化学工业出版社, 2016.

2. 龚勋. 邢涛. 菜谱大全[M]. 云南: 云南教育出版社, 2010.

3. 杜栋, 庞华庆, 吴英. 现代综合评价方法与案例精选[M]. 北京: 清华大学出版社, 2008.

4. 姜启源, 谢金星, 叶俊. 数学模型(第四版) [M]. 高等教育出版社, 2017.

5. 武松, 潘发明. SPSS统计分析大全[M]. 北京: 清华大学出版社, 2014.

附录

model:

!Lingo 求解双目标多元线性整数规划;

min=21/78*(x1*6+x2*2+x3*7+x4*3+x5*1.6+x6*6+x7*7+x8*2.4)-57/78*(x1*6.18+x2*5.77+x3*6.96+x4*5.72+x5*5.68+x6*7.14+x7*6.84+x8*5.9);

16.7*x1+6.6*x2+6.42*x3+9.075*x4+2.5*x5+15*x6+7.55*x7+4.822*x8>=(75*0.7-4*2.6)/4;

35.4*x1+5.65*x2+14.92*x3+7.392*x4+0.2*x5+1.5*x6+18.6*x7+10.801*x8>=(50*0.7-4*0.3)/4;

0.35*x2+0.72*x3+0.396*x4+2.1*x5+0.6*x7+0.639*x8>=(30*0.7-4*0.2)/4;

0.07*x1+0.165*x2+0.141*x3+0.2409*x4+0.05*x5+0.01*x6+0.155*x7+0.0851*x8>=(1.35*0.7-4*0.02)/4;

0.07*x1+0.165*x2+0.082*x3+0.2211*x4+0.17*x5+0.07*x6+0.095*x7+0.0748*x8>=(1.3*0.7-4*0.03)/4;

37*x1+231.5*x2+25.8*x3+305.91*x4+29*x5+6*x6+22.5*x7+26.59*x8>=(800*0.7-4*7)/4;

1.7*x1+1.25*x2+1.48*x3+1.98*x4+1.5*x5+4.1*x6+1.5*x7+0.89*x8>=(17.5*0.7-4*2.2)/4;

1.1*x1+0.54*x2+0.962*x3+0.7425*x4+0.54*x5+1.17*x6+1.145*x7+1.0305*x8>=(15.5*0.7-4*1.36)/4;

x1+x2+x3+x4+x5+x6+x7+x8=4;

@bnd(0,x1,2);

@bnd(0,x2,2);

@bnd(0, x3,2);

@bnd(0,x4,2);

@bnd(0,x5,2);

@bnd(0, x6,2);

@bnd(0,x7,2);

@bnd(0,x8,2);

@gin(x1);

@gin(x2);

@gin(x3);

@gin(x4);

@gin(x5);

@gin(x6);

@gin(x7);

@gin(x8);

单位菜品营养元素系数计算模型程序：

function B=fenlei(A);

A=input('请输入菜品材料比例')%以矩阵表示，小数表示所占比例，无该种材料则为0，牛肉，猪肉，鱼肉，鸡肉，鸭肉，豆类，根茎类，菌类，叶类，干豆类，瓜果类，鸡蛋的顺序

G=[18.1,13.2,16.6,16.7,15,2.5,1.9,1.9,1.4,0.4,8.1,12.8

13.4,37,5.2,35.4,1.5,0.2,0.2,0.3,0.1,0.2,3.7,11.1

0,0,0,0,0,2.1,1.2,2.3,0.9,0.7,0.4,0

8,6,38,37,6,29,39,5,35,19,164,444

3.2,1.6,0.8,1.7,4.1,1.5,1.4,1,0.6,0.2,1.9,2.3

3.67,2.06,0.87,1.1,1.17,0.54,0.23,0.61,0.61,0.07,1.11,1.01

0.03,0.22,0.04,0.07,0.01,0.05,0.09,0.06,0.03,0.01,0.03,0.32

0.11,0.16,0.11,0.07,0.07,0.17,0.03,0.16,0.04,0.01,0.03,0.32];

M=zeros(8,12);

if any(abs(A)>0);

i=1;

while i<=12

if A(i)>0;

M(:,i)=G(:,i);

else

M(:,i)=[0 0 0 0 0 0 0 0]'

end

i=i+1;

end

else

i=1;

while i<=12

M(:,i)=[0 0 0 0 0 0 0 0]';

i=i+1;

end

M%输出顺序为蛋白质，脂肪，膳食纤维，维生素b1，维生素b2，钙，铁，锌

购买趋势数计算程序：

function D=goumaiqushishu(C,E);%

C=input('请输入菜品满意度');

E=input('请输入菜品价格'); %菜品满意度和价格都已矩阵的形式输入，例如3道菜则[1 2 3]

D=57/78*C-21/78*E

NOTES

^*通讯作者。

期刊菜单