Advances in Applied Mathematics
Vol.
07
No.
09
(
2018
), Article ID:
26807
,
17
pages
10.12677/AAM.2018.79137
Application of Green’s Formula in Differential Equations
Yue Zhou, Yanqin Xiong*
School of Mathematics and Statistics, Nanjing University of Information Science and Technology, Nanjing Jiangsu

Received: Aug. 21st, 2018; accepted: Sep. 7th, 2018; published: Sep. 13th, 2018

ABSTRACT
This paper investigates the Green’s function solution of common non-homogeneous ordinary differential equations and partial differential equations. We first obtain Green’s functions according to the physical meanings of special partial differential equations. Then we yield their solutions. Considering non-homogeneous ordinary differential equations with insignificant physical meanings, this paper begins with the simplest first-order linear equations. Furthermore, the Green’s function of higher-order linear equations is derived.
Keywords:Green’s Function, Ordinary Differential Equations, Partial Differential Equations, Green’s Formula
格林公式在微分方程中的应用
周悦,熊艳琴*
南京信息工程大学数学与统计学院,江苏 南京

收稿日期:2018年8月21日;录用日期:2018年9月7日;发布日期:2018年9月13日

摘 要
本文研究了常见的非齐次常微分方程和偏微分方程的格林函数解法。本文首先根据特殊的偏微分方程的物理意义分别求出了它们的格林函数,从而得到了它们的解。对于物理意义不明显的非齐次常微分方程,本文从最简单的一阶线性方程开始讨论,进一步地,推导出了高阶线性方程的格林函数。
关键词 :格林函数,常微分方程,偏微分方程,格林公式

Copyright © 2018 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
格林函数别名为点源函数或影响函数,从字面意义上理解,即表示在特定的边界条件或初值条件下一个点源所产生的场和影响。因为许多点源产生的场的叠加可被看作是任意分布的源所产生的场,所以一旦求出格林函数,就可以算出任意源的场。
1828年,乔治·格林(1793~1841)发表了《论数学分析在电磁理论上的应用》 [1] ,在这篇著作中,格林试图确定由特定电势的导体在真空中的电势。用已知的符号,我们可以说格林想要得到在区域V中且满足特定边界条件S, 的解。
为了解决这个问题,格林首先考虑源是一个点电荷的问题。在现代理论中,他试图求解如下的偏微分方程:
(1)
这里 是狄拉克 函数。我们现在知道方程(1)的解为 ,这里 。注意到G的奇异性,他继续研究。首先,他证明了以他名字命名的定理:
(2)
这里n代表外法线方向, 和 是标量函数且导数有界,然后在 处放置一个奇异性的小球(因为方程(2)在这里不适用),之后从区域V中排除这个点,因为当小球的半径趋于0时,小球的曲面积分为 ,他得到
接下来,格林要求G在曲面S上满足齐次边界条件 。由于在V内(不包括 ), ,当 (Laplace方程)时,对S中的任意点r,他发现
这里 表示u在S上的值。一旦G已知,则边值问题可解。格林认为G一定存在,它在物理上表示位于 点处的点电荷的电势。
格林的这篇论文早期几乎无人问津,直到1854年,开尔文重新发现了格林被埋没的名作。二十世纪之初,Poincaré [2] 总结了格林函数的性质。1946年菲利普·M·莫尔斯和赫尔曼·费什巴赫合著了《理论物理方法》 [3] ,格林函数的随后研究便可以在这个时间点之后分为两个部分。20世纪30年代后期,他们开始教物理系的学生数学方法,在这些课堂笔记中,他们发现了格林函数具备的四个性质。莫尔斯和费什巴赫的最大贡献是证明了“格林函数是边值问题的点源解”。到了1960年,许多教科书开始介绍格林函数的用法。例如,在Mackie的书 [4] 中,他概括地说明了一些数学方法,特别是格林函数和积分变换的方法,可以用来解决常微分方程和偏微分方程中常见的边值问题。在 [5] - [10] 中,学者们纷纷研究了用格林函数求解位势方程、热传导方程、二维和三维波动方程、Laplace方程的初边值问题。格林函数法的显著优势为它把具有任意非齐次项和边值的定解问题转化为求解一个特定的边值问题,它仅依赖于微分算子、边界条件的形式和该区域的形状。格林函数法用统一的方式处理各类数学物理方程,既可以求解偏微分方程 [11] ,又可以求解常微分方程 [12] [13] [14] ;既可以处理齐次方程,也可以处理非齐次方程;既可以研究有界问题,又可以分析无界问题。格林函数法的优越性使得它的应用十分广泛。格林函数在求解常微分方程和偏微分方程边值问题以及初边值问题中具有特殊的重要性。
在这篇文章中,我们主要研究了常见的偏微分方程和常微分方程的格林函数。
2. 格林公式
Gaussy公式:设空间闭域 是由光滑或分段光滑的双侧封闭曲面
所围成,函数
,
,
在
上具有一阶连续偏导数,则成立如下Gauss公式:
是由光滑或分段光滑的双侧封闭曲面
所围成,函数
,
,
在
上具有一阶连续偏导数,则成立如下Gauss公式:
(3)
这里 是 的整个边界曲面的外侧,其中n是 的单位外法线方向, , , 是n的方向余弦。
2.1. 第一格林公式
设函数 ,在式(3)中取
得
计算并利用
得

或
(4)
其中 为v沿方向n的方向导数, 为u的梯度,式(4)为第一格林公式。
2.2. 第二格林公式
将式(4)中的u,v位置互换,得
(5)
将(4)式与(5)式相减,得第二格林公式:
(6)
3. 格林函数
由格林公式,可以引入三维空间的基本积分公式。
3.1. 基本积分公式
定理3.1设函数 ,则当点
时,有
,则当点
时,有
其中 ,n是 的单位外法线方向。
若u是调和函数(即 ),则成立三维调和函数的基本积分公式:
(7)
3.2. 格林函数的定义
为求解Laplace方程的Dirichlet边值问题
(8)
我们引进格林函数的概念。
公式(7)使我们想到求解边值问题(8),要求出未知函数u在区域 内的值,必须同时知道函数u和 在边界 上的值,在(7)中能否消去 这一项,我们应用格林第二公式于函数u和调和函数v,有
(9)
(7) + (9),得
如果选取调和函数v满足
则可消去 这一项,因此有
令
则有
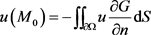
从而Laplace方程的Dirichlet问题的解便表示为
(10)
称 为Laplace方程Dirichlet问题在区域 上的格林函数。
4. 格林函数的性质
定理 [15] 4.1. 格林函数 除
外,处处满足方程
,当
时,
,其阶数和
相等。
除
外,处处满足方程
,当
时,
,其阶数和
相等。
定理 [15] 4.2. 在边界 上, .
定理 [15] 4.3. 在区域 内, .
定理 [15] 4.4. .
定理 [15] 4.5. 格林函数
具有对称性,即对
, 。
。
5. 格林函数在偏微分方程中的应用
格林函数在物理学中的意义 [16] :设在点 处放置一单位正电荷,则在自由空间 内的M点处的电位为 ,若封闭的导电面 外层接地,则内层感应电荷将会产生一个附加电场,附加电场对M点的电位为 ,此时在导电面内的电位为
5.1. 半空间的Green函数及Dirichlet边值问题
求 半空间的Green函数,并求解下列Dirichlet边值问题
(11)
求Green函数 ,由Green函数在物理学中的意义,在 处放置一单位正电荷,它在点M处产生的电位是 ,在 关于 的对称点 处置一单位正电荷,它在点M处产生的电位是 ,如图1所示。
由它们所形成的静电场的电位在平面 上恰好为零,因此上半平面的Green函数为
要求边值问题(11)的解,只需计算 ,因此在平面 上的外法线是z轴的负向,因此
(12)

Figure 1. The mirror image method
图1. 镜像法
将(12)代入(10)得到(11)的解为
5.2. 球体区域的Green函数及Dirichlet边值问题
求解球体区域的Green函数和下面的Dirichlet边值问题
(13)
其中 是以O为圆心,R为半径的球域,它的边界为 。
先求球体的Green函数。在球 内任取一点 ,用 表示它到原点O的距离,在射线 上取一点 ,如图2所示。
使得
(14)
其中
为点
到原点O的距离,把
称为点 关于球面
的对称点。在球面上任取一点
,它到点
,
的距离分别为
。对于三角形
,它们有一个公共角
,由(14)易知,这两个三角形相似,于是
关于球面
的对称点。在球面上任取一点
,它到点
,
的距离分别为
。对于三角形
,它们有一个公共角
,由(14)易知,这两个三角形相似,于是
由此易得,对于球内任一点 ,只要取函数
则球 上的Green函数有如下形式
(15)
为求(13)的解,要计算
。设a表示OM与 之间的夹角,r为点M到原点O之间的距离,则有
之间的夹角,r为点M到原点O之间的距离,则有

Figure 2. Sphere area
图2. 球体区域
代入(15)得
它在球面 的方向导数为
故(13)的解为
6. 格林函数在常微分方程中的应用
在上一节中,我们讨论了格林函数在偏微分方程中的作用,本节将继续讨论格林函数在常微分方程中的应用。
6.1. 预备知识
函数是由物理学家狄拉克首先引进的。在数学上,可以把 函数看成广义函数。传统意义上, 函数的定义 [17] 是
且 .
函数一般具有下列性质 [18] :
1)
2)
3)
在求解非齐次的常微分方程初值问题时,除了常用的“常数便易法”,我们还可以考虑用格林函数法求解。格林函数在常微分方程中的应用始于1894年 [19] ,注意到格林函数用于解决二维和三维泊松公式,H. Burkhardt [20] (1861~1914)想知道格林函数能否用来解决如下问题
他证明了这个问题的解可以写为
他更简略地把解表示为
物理上,非齐次项
表明外界的扰动,而格林函数与非齐次项无关,只要求出格林函数,可以代入同一个积分
。我们注意到非齐次项 可以利用
函数来表示
可以利用
函数来表示
下面,我们讲具体讨论如何求出对应的格林函数。
6.2. 一阶非齐次常微分方程
考虑如下的一阶线性非齐次方程
(16)
初始条件为
格林函数 被定义 [21] 为
的解。
非齐次方程(16)的解可以用含有格林函数的积分来表示。
为了证明 是方程的解,我们将线性算子应用于积分(假定积分是一致收敛的)。
积分仍然满足初始条件
现在,我们考虑格林函数的定性行为。当
时,格林函数仅是微分方程的一个齐次解,而
时,我们能得到一些奇解。 有一个狄拉克
函数型的奇点,这表明
在
处有一个跳跃间断点,在区间
上对微分方程进行积分来确定这个跳跃点。
有一个狄拉克
函数型的奇点,这表明
在
处有一个跳跃间断点,在区间
上对微分方程进行积分来确定这个跳跃点。
(17)
微分方程的齐次解为

因为格林公式满足 时的齐次解,所以 和 时,它是这个齐次解的常数倍。
为了满足齐次初始条件 ,则
跳跃条件(方程(17))给出了约束条件 ,这决定了 时齐次解的常数。则
我们可以用赫维赛德函数 来表示格林函数
来表示格林函数
6.3. 二阶非齐次常微分方程
考虑二阶非齐次方程
格林函数 被定义为
(18)
的解。
为了证明 为方程(18)的解,我们将线性算子应用于积分(假定积分是一致收敛的)。
此积分仍然满足边界条件
利用格林函数求解常微分方程的优点之一是只需要找到线性算子和特定的齐次边界条件的格林函数
对任何非齐次问题都可以表示解
不需要额外的其他步骤来求一个非齐次微分方程的解。
二阶微分方程的格林函数有什么性质?它会有一个 函数型的奇点吗?它会是连续的吗?回答这些问题,我们将首先研究 的积分和微分的性质。
对
进行积分得到赫维赛德函数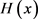
对赫维赛德函数 进行积分,得到斜坡函数
当 时, 的导数为0;在 处,它的导数从0上升到 ,下降到 然后回到0。
我们写出格林函数的微分方程
我们发现只有 可以有一个 函数型的奇点.如果其他项具有 函数型的奇点,那么 将比 函数更奇异,并且在方程的右侧将不存在匹配这种奇异性的任何项。类似于从 函数到赫维赛德函数到斜坡函数的过程,我们看到 有一个跳跃间断点, 是连续的。
设 是齐次微分方程 的两个线性无关解。当 时,格林函数满足齐次微分方程,因此它是齐次解的线性组合。
我们要求 是连续的
我们可以用齐次解来表示
对 在 上积分,得
因为 是连续的, 有一个跳跃间断点,所以
我们用齐次解来表示这个跳跃条件
结合这两个边界条件,共有四个方程来确定四个常数 的值。
6.4. 斯特姆-刘维尔问题
一般的二阶线性方程总可以化成如下这种形式:
(19)
边界条件 。
这就是斯特姆-刘维尔问题。要求格林函数,应当使格林函数满足如下条件:
设 是方程(19)对应的齐次方程的两个非零解(分别满足左、右边值条件),即
当 时,格林函数满足的微分方程退化为齐次方程,因此可以改写如下形式
这里, 是关于 的未知函数,由连续性条件
将非齐次方程写成标准形式
由跳跃条件,
得到可以求出 的方程组
用克拉默法则求解方程组,得
这里, 是 和 的伏朗斯基行列式。因此,格林函数为
6.5. 初值问题
考虑
由于非齐次的线性微分方程初值问题满足叠加原理,不妨设解 ,这里
因为伏朗斯基行列式
非零,所以v的微分方程的解是线性无关的,因此存在满足初值条件的v的唯一解。
关于u,格林函数满足 [22]
连续条件和跳跃条件为
设 为微分方程的两个线性无关解,当 时, 是这些解的线性组合,因为伏朗斯基行列式非零,故只有平凡解满足齐次初值条件,格林函数为
这里 是 的线性组合,且满足
注意到伏朗斯基行列式非零,因此确定了 的唯一解。我们可以将格林函数写成如下形式
故关于u的方程的解可表示为
故
6.6. 混合边值问题
考虑
给定初边值条件
由叠加原理,不妨设通解 ,这里u和v分别满足
其中,v的问题可能无解,有唯一解或有无穷多解。我们仅考虑v有唯一解的情况。在这种情况下,齐次方程的齐次边界问题只有平凡解 [23] 。
设 和 是满足齐次边界条件 和 的齐次常微分方程的解,又因为完全齐次问题无解,则 和 非零。解v有如下形式
应用两个边界条件,得
关于u的方程,格林函数满足
连续条件和跳跃条件分别是
格林函数则可以写成
这种形式下,则跳跃条件和连续条件已经满足,应用边界条件,得
由于 和 非零,定义的格林函数有意义。
故y的通解为
6.7. 高阶非齐次常微分方程
考虑n阶微分方程
满足边界条件
这里
假定微分方程的系数函数在 上连续。通解 ,这里u和v分别满足
下面我们将用格林函数来表示这个解。
首先我们考虑关于v的齐次常微分方程初值问题。设 是一组线性无关的解的集合,则 ,这里常数由下面的矩阵方程决定
为了求解关于u的问题,我们考虑满足下列等式的格林函数
让 是满足下列条件的齐次解的组合:
因此解为
格林函数形式为
常数被如下的矩阵方程所决定
故
7. 结论
格林函数理论是求解非齐次线性微分方程的一种方法。由上述讨论,格林函数 满足的微分方程在 时退化为齐次方程,理论上比原方程更易求解。
对于非齐次常微分方程,我们首先要构造格林函数,导出格林函数应该满足的微分方程和边值条件。因为格林函数只依赖边值条件,与非齐次项(源)无关。一旦求出格林函数,非齐次常微分方程的解 [24] 为
对于偏微分方程的有限区域给定边界问题,格林函数的求解则会困难得多,要视具体情况而定,可能会用到镜像法、模式展开法、Fouier方法等 [25] 。本文所述的只是格林公式在方程中的应用的一小部分,格林公式在其他方程中的应用有待于我们作进一步的深层研究。
文章引用
周悦,熊艳琴. 格林公式在微分方程中的应用
Application of Green’s Formula in Differential Equations[J]. 应用数学进展, 2018, 07(09): 1174-1190. https://doi.org/10.12677/AAM.2018.79137
参考文献
- 1. Turner, R.D. (1956) The Diffraction of a Cylindrical Pulse by a Half-Plane. Stichting Mathematisch Centrum Toegepaste Wiskunde, 14, 1-12. https://doi.org/10.1090/qam/78911
- 2. Lowan, D.A. (1938) VI. On the Operational Determination of Green’s Functions in the Theory of Heat Conduction. Philosophical Magazine, 24, 62-70. https://doi.org/10.1080/14786443708561890
- 3. Carrier, G.F. and Pearson, C.E. (1976) CE Partial Differential Equations. Academic Press, New York.
- 4. Burkhardt, H. (1894) Sur les Fonctions de Green Relatives à un Domaine d’une Dimension. Bulletin de la Société Mathématique de France, 22, 71-75. https://doi.org/10.24033/bsmf.484
- 5. Bôcher, M. (1901) Green’s Functions in Space of One Dimension. Bulletin of the American Mathematical Society, 7, 297-299. https://doi.org/10.1090/S0002-9904-1901-00802-6
- 6. Whyburn, W.M. (1924) An Extension of the Definition of the Green’s Function in One Dimension. Annals of Mathematics, 26, 125-130. https://doi.org/10.2307/1967748
- 7. 王定江. 应用偏微分方程[M]. 杭州: 浙江大学出版社, 2007: 113-116.
- 8. Onida, G., Reining, L. and Rubio, A. (2002) Electronic Excitations: Densi-ty-Functional versus Many-Body Green’s-Function Approaches. Reviews of Modern Physics, 74, 601-659. https://doi.org/10.1103/RevModPhys.74.601
- 9. 闵琦. δ函数的定义及其性质[J]. 大学物理, 2004(9): 18-20.
- 10. Barton, G. (1989) Elements of Green’s Functions and Propagation: Potentials, Diffusion, and Waves. Oxford University Press, Oxford, 3-5.
- 11. Duffy, D.G. (1982) Green’s Functions with Applications. Second Edition, CRC Press, New York, 20-21.
- 12. Armand, G., Manson, J.R. and Jayanthi, C.S. (1986) Thermal Attenuation in Atom-Surface Scattering: The Multiphonon Contribution. Physical Review B Condensed Matter, 34, 6627.
- 13. Roach, G. (1982) Green’s Function. Cambridge University Press, Cambridge, 2-3.
- 14. Stakgold, I. (1998) Green’s Functions and Boundary Value Problems. Wiley, New York.
- 15. Javadpour, S.H. and Ahmadi, A.R. (1993) An Introduction to Ordinary and Partial Differential Equations. Springer, Cham.
- 16. Yang, X. (2003) Green’s Function and Positive Solutions for Higher-Order ODE. Applied Mathematics and Computation, 136, 379-393. https://doi.org/10.1016/S0096-3003(02)00056-5
- 17. Green, G., Wheelhouse, T. and Lindsay, R.B. (2008) An Essay on the Application of Mathematical Analysis to the Theories of Elec-tricity and Magnetism. Journal Für Die Reine Und AngewandteMathematik, 1850, 73-89.
- 18. Poincaré, M.H. (1894) Sur les équations de la physique mathématique. Rendiconti del CircoloMatematico di Palermo, 8, 57-155. https://doi.org/10.1007/BF03012493
- 19. Morse, P.M.C. and Feshbach, H. (1946) Methods of Theoretical Physics. Technology Press, New York.
- 20. Payne, L.E. and Mackie, A.G. (1966) Boundary Value Problems. American Mathematical Monthly, 73, 910. https://doi.org/10.2307/2314220
- 21. Neumann, C. (2009) Ueber die Integration der Partiellen Differentialgleichung: . Journal Für Die Reine Und AngewandteMathematik, 1861, 335-366. https://doi.org/10.1515/crll.1861.59.335
- 22. 姜礼尚, 孔德兴, 陈志浩. 应用偏微分方程讲义[M]. 北京: 高等教育出版社, 2011: 38-42.
- 23. Thomson, W. (2013) On the Theory of the Electric Telegraph. Proceedings of the Royal Society of London, 7, 382-399. https://doi.org/10.1017/CBO9780511996016.009
- 24. Cagniard, L. (1935) Diffraction d’uneonde Progressive par un Écranenforme de Demi-plan. Journal de Physique et le Radium, 6, 369-372. https://doi.org/10.1051/jphysrad:0193500609036900
- 25. Schouten, G. (1999) Two-Dimensional Effects in the Edge Sound of Vortices and Dipoles. The Journal of the Acoustical Society of America, 106, 3167-3177. https://doi.org/10.1121/1.428171
NOTES
*通讯作者。