Advances in Applied Mathematics
Vol.
08
No.
02
(
2019
), Article ID:
28859
,
8
pages
10.12677/AAM.2019.82026
Existence of Multiple Positive Solutions of Differential Equation System with Two-Point Boundary Value
Xuan Zhong
Department of Mathematics, Nanjing University of Aeronautics and Astronautics, Nanjing Jiangsu
Received: Jan. 23rd, 2019; accepted: Feb. 7th, 2019; published: Feb. 14th, 2019

ABSTRACT
This paper deals with a class of two-point boundary value problems for differential equation system with parameters. Using fixed point index theory, existence of one positive solution and two positive solutions are obtained to this class of systems.
Keywords:Two-Point Boundary Value Problem, Fixed Point Index, First Eigenvalue, Green’s Function
两点边值微分方程组多重正解的存在性
钟 璇
南京航空航天大学数学系,江苏 南京
收稿日期:2019年1月23日;录用日期:2019年2月7日;发布日期:2019年2月14日

摘 要
本文研究了一类含参数微分方程组的两点边值问题。运用不动点指数理论,我们得到了方程组存在一个正解以及两个正解的结果。
关键词 :两点边值问题,不动点指数理论,第一特征值,格林函数

Copyright © 2019 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
近年来,四阶微分方程边值问题广泛出现在医学、物理学、生物学等领域,受到了学者的密切关注。由于四阶边值问题起源于弹性梁状态问题的数学模型,此类问题研究比较活跃,有很多学者对四阶方程两点边值问题运用锥拉伸锥压缩不动点定理,上下解方法,单调迭代方法等进行了很好的研究 [1] - [7] ,但是有关复合型的微分方程组边值问题的研究并不多见。文献 [8] 研究了如下四阶复合型微分方程组边值问题多个正解的存在性:
其中非线性项
,
,且
。
受以上文献的启发,本文将考察如下含有
的一类耦合奇异半正微方程组的两点边值问题,通过讨论
的取值,得出
对其正解的存在性及多解性的影响。方程如下:
(1)
假设方程满足如下条件:
(H1)
,且
连续;
(H2)
,
,对
,
,其中
;
(H3)
,且为常数。
定义
为定义在闭区间
上全体连续函数构成的集合,在
上定义范数
,
,在E中取范数
。为了叙述方便,我们引入下列记号
显然K为E中的正规锥。
2. 预备知识
引理1 [1] :(锥拉伸与锥压缩不动点定理)设
与
是无穷维实Banach空间E中的两个有界开集,并且
,
是全连续算子,如果下列条件之一满足:
1)
。
2)
。
则算子A在
中有不动点。
引理2 [4] :边值问题
的格林函数为:
且具有下列性质:
1、当
时,有
,
。
2、
。
由此问题(1)的解等价于
的解。
记
定义算子:
显见问题(1)的解等价于算子T的不动点。
引理3:若方程满足(H1)-(H3),则算子T是全连续的,且
。
证明:由全连续算子的定义易证算子T全连续,下证
。由引理1性质2得
,
,
,则
,当
时,有
即
,
,所以
。
引理4 [9] :设L:
为线性全连续算子,且
,其中K是
中的锥,如果存在
及常数
,使得
,则L的谱半径
且L有一个相应于第一个特征值
的正特征函数
,即
。
引理5:设(H1)-(H3)成立,则算子T的谱半径
,且T有一个对应于第一个特征值
的正特征函数。
证明:因为T为全连续算子,且
。由条件(H1),(H2)知存在
,使得
因此,存在
,使得对于
,满足
,
。
取
,满足
且
,则
又由(H3):
,以及
可得,存在常数
,使得
。由引理4得算子T的谱半径
,且T有一个对应于第一个特征值
的正特征函数。
设
为线性边值问题
的第一个特征值,
为线性边值问题
的第一个特征值,则
。从而
的谱半径
,
的谱半径
。假设它们相对应的特征函数分别为
。则满足
,否则如果
,则
其中
,从而矛盾,不妨设
.在E上定义泛函:
则对
,
。令
,
则
(2)
并且满足:
即
(3)
3. 主要结果
定理1:若条件(H1)~(H3)成立,且
,则问题(1)至少有一个正解。
证明:以下证明分两步
1) 由
可得
且充分小,使得当
时,对 ,恒有
,恒有 。
。
令 ,假设存在
,假设存在 和
和 满足
满足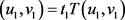 ,则由(3)式得
,则由(3)式得
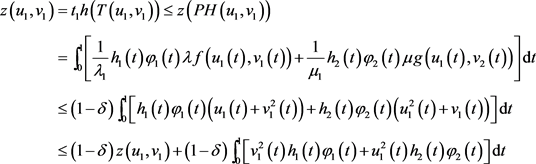
即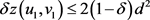 ,由(2)式得
,由(2)式得 ,即
,即 ,这与d充分小矛盾。根据不动点指数的同伦不变性得
,这与d充分小矛盾。根据不动点指数的同伦不变性得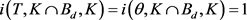 。
。
2) 由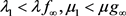 可得,
可得, ,使得当
,使得当 时,有
时,有 ,
,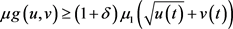 。又当
。又当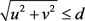 时,
时,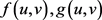 有界,故存在常数
有界,故存在常数 ,使得当
,使得当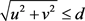 时,对
时,对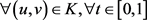 ,恒有
,恒有
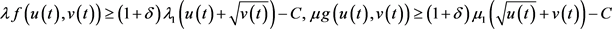
取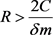 ,令
,令 ,假设存在
,假设存在 和
和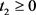 满足
满足 ,其中
,其中 ,则由(3)可得
,则由(3)可得

所以 ,这与
,这与 矛盾,从而假设不成立。故当R充分大时
矛盾,从而假设不成立。故当R充分大时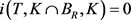 。再由不动点指数的可加性,得
。再由不动点指数的可加性,得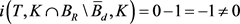 。从而算子T至少有一个不动点,即方程至少有一个解。
。从而算子T至少有一个不动点,即方程至少有一个解。
定理2:若条件(H1)~(H3)成立,且 ,则问题(1)至少有一个正解。
,则问题(1)至少有一个正解。
证明:以下证明分两步
1) 由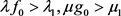 可得
可得 ,使得当
,使得当 时,对
时,对 ,有
,有
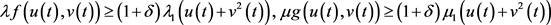
假设存在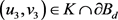 和
和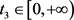 ,满足
,满足 ,其中
,其中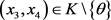 ,则由(3)可得
,则由(3)可得
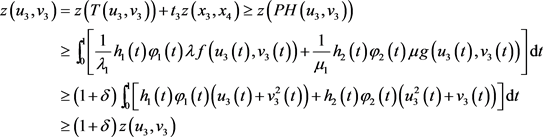
即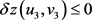 ,这与(2)式
,这与(2)式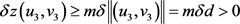 矛盾,从而假设不成立。由不动点指数的缺方向性知,当d充分小时,有
矛盾,从而假设不成立。由不动点指数的缺方向性知,当d充分小时,有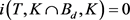 。
。
2) 又由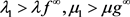 可得,
可得,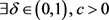 ,使得
,使得 时,有
时,有

取R充分大,满足 ,假设存在
,假设存在 和
和 满足
满足 ,则由(3)式得
,则由(3)式得
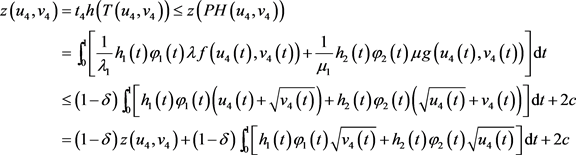
所以
又因为 ,从而
,从而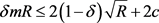 。这与R的选取矛盾,故当R充分大时,有
。这与R的选取矛盾,故当R充分大时,有 。再由不动点指数的可加性得
。再由不动点指数的可加性得 。从而算子T至少有一个不动点,即方程至少有一个解。
。从而算子T至少有一个不动点,即方程至少有一个解。
定理3:若条件(H1)~(H3)成立,对于 ,若存在数
,若存在数 ,使得当
,使得当 时,恒有
时,恒有
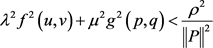
成立,其中 ,那么问题(1)至少有两个正解。
,那么问题(1)至少有两个正解。
证明:令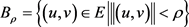 ,其中
,其中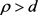 ,若存在
,若存在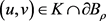 和
和 ,满足
,满足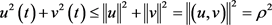 ,由
,由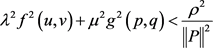 可得
可得
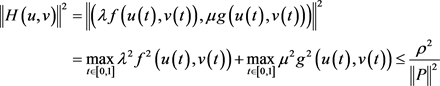
从而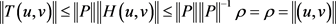 ,故由锥压缩定理知
,故由锥压缩定理知 。
。
利用定理1的第二步和定理2的第一步证明及不动点指数的可加性可得
 ,
,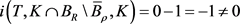
由不动点指数的可解性知,算子T在 和
和 中分别至少有一个不动点,所以问题(1)至少有两个正解。
中分别至少有一个不动点,所以问题(1)至少有两个正解。
定理4:若条件(H1)-(H3)成立,对于 ,若存在数
,若存在数 ,使当
,使当 ,
, 时,恒有
时,恒有

成立,其中 ,则问题(1)至少有两个正解。
,则问题(1)至少有两个正解。
证明:若存在 和
和 ,满足
,满足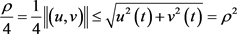 ,
,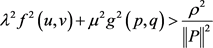 得
得

即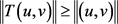 ,故由锥压缩定理知,
,故由锥压缩定理知, 。
。
利用定理1的第一步和定理2的第二步证明及不动点指数的可加性可得
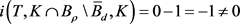 ,
,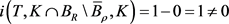
由不动点指数的可解性知,算子T在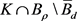 和
和 中分别至少有一个不动点,所以问题(1)至少有两个正解。
中分别至少有一个不动点,所以问题(1)至少有两个正解。
致谢
感谢导师陈芳启教授的悉心指导!
基金项目
国家自然科学基金(11872201)。
文章引用
钟 璇. 两点边值微分方程组多重正解的存在性
Existence of Multiple Positive Solutions of Differential Equation System with Two-Point Boundary Value[J]. 应用数学进展, 2019, 08(02): 227-234. https://doi.org/10.12677/AAM.2019.82026
参考文献
- 1. 郭大钧. 非线性泛函分析[M]. 第3版. 济南: 山东科技出版社, 1985: 243-244.
- 2. 姚庆六, 白占兵. 的边值问题的正解存在性[J]. 数学年刊: 中文版, 1999(5): 575-578.
- 3. 席莉静. 一类算子方程的多重正解及对奇异边值问题的应用[J]. 苏州科技大学学报(自然科学版), 2004, 21(3): 26-30.
- 4. 陈丽珍, 李刚. 四阶非线性微分方程组正解的存在性[J]. 扬州大学学报(自然科学版), 2008, 11(4): 25-28.
- 5. 王全义, 邹黄辉. 一类四阶奇异非线性积分边值问题正解的存在性[J]. 华侨大学学报, 2014, 35(1): 83-87.
- 6. 赵微. 一类四阶微分方程m点边值问题的正解[J]. 四川师范大学学报(自然科学版), 2017, 40(6): 791-796.
- 7. Jankowski, T. (2010) Positive Solutions for Fourth-Order Differential Equations with Deviating Argu-ments and Integral Boundary Conditions. Nonlinear Analysis, 73, 1289-1299. https://doi.org/10.1016/j.na.2010.04.055
- 8. 马田田, 赵增勤. 非线性微分方程组边值问题多个正解的存在性[J]. 工程数学学报, 2009, 26(6): 1050-1056.
- 9. 周韶林, 吴红萍, 韩晓玲. 一类四阶三点边值问题正解的存在性[J]. 四川大学学报(自然科学版), 2014, 51(1): 11-15.





 ,恒有
,恒有 。
。 ,假设存在
,假设存在 和
和 满足
满足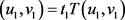 ,则由(3)式得
,则由(3)式得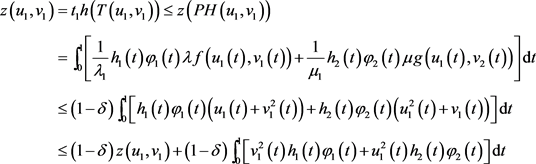
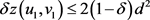 ,由(2)式得
,由(2)式得 ,即
,即 ,这与d充分小矛盾。根据不动点指数的同伦不变性得
,这与d充分小矛盾。根据不动点指数的同伦不变性得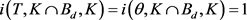 。
。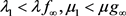 可得,
可得, ,使得当
,使得当 时,有
时,有 ,
,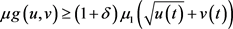 。又当
。又当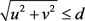 时,
时,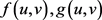 有界,故存在常数
有界,故存在常数 ,使得当
,使得当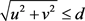 时,对
时,对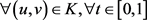 ,恒有
,恒有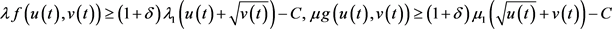
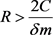 ,令
,令 ,假设存在
,假设存在 和
和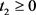 满足
满足 ,其中
,其中 ,则由(3)可得
,则由(3)可得
 ,这与
,这与 矛盾,从而假设不成立。故当R充分大时
矛盾,从而假设不成立。故当R充分大时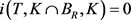 。再由不动点指数的可加性,得
。再由不动点指数的可加性,得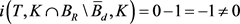 。从而算子T至少有一个不动点,即方程至少有一个解。
。从而算子T至少有一个不动点,即方程至少有一个解。 ,则问题(1)至少有一个正解。
,则问题(1)至少有一个正解。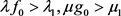 可得
可得 ,使得当
,使得当 时,对
时,对 ,有
,有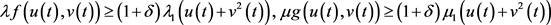
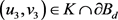 和
和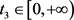 ,满足
,满足 ,其中
,其中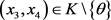 ,则由(3)可得
,则由(3)可得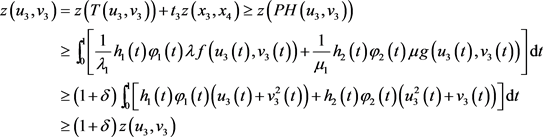
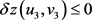 ,这与(2)式
,这与(2)式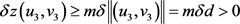 矛盾,从而假设不成立。由不动点指数的缺方向性知,当d充分小时,有
矛盾,从而假设不成立。由不动点指数的缺方向性知,当d充分小时,有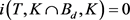 。
。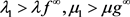 可得,
可得,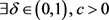 ,使得
,使得 时,有
时,有
 ,假设存在
,假设存在 和
和 满足
满足 ,则由(3)式得
,则由(3)式得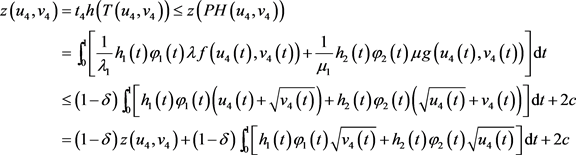

 ,从而
,从而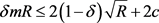 。这与R的选取矛盾,故当R充分大时,有
。这与R的选取矛盾,故当R充分大时,有 。再由不动点指数的可加性得
。再由不动点指数的可加性得 。从而算子T至少有一个不动点,即方程至少有一个解。
。从而算子T至少有一个不动点,即方程至少有一个解。 ,若存在数
,若存在数 ,使得当
,使得当 时,恒有
时,恒有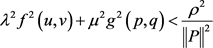
 ,那么问题(1)至少有两个正解。
,那么问题(1)至少有两个正解。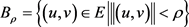 ,其中
,其中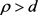 ,若存在
,若存在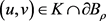 和
和 ,满足
,满足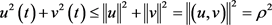 ,由
,由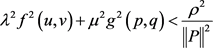 可得
可得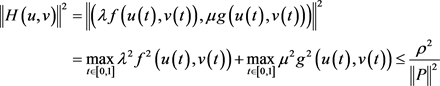
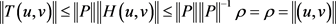 ,故由锥压缩定理知
,故由锥压缩定理知 。
。 ,
,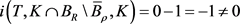
 和
和 中分别至少有一个不动点,所以问题(1)至少有两个正解。
中分别至少有一个不动点,所以问题(1)至少有两个正解。 ,若存在数
,若存在数 ,使当
,使当 ,
, 时,恒有
时,恒有
 ,则问题(1)至少有两个正解。
,则问题(1)至少有两个正解。 和
和 ,满足
,满足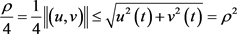 ,
,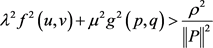 得
得
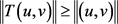 ,故由锥压缩定理知,
,故由锥压缩定理知, 。
。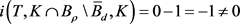 ,
,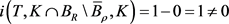
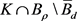 和
和 中分别至少有一个不动点,所以问题(1)至少有两个正解。
中分别至少有一个不动点,所以问题(1)至少有两个正解。