Advances in Applied Mathematics
Vol.
10
No.
07
(
2021
), Article ID:
43818
,
10
pages
10.12677/AAM.2021.107242
一类非齐次变型Bessel方程边值问题的构造解法及应用
李伟1,张松林2,刘浩瀚3,李顺初1
1西华大学理学院,四川 成都
2宜宾职业技术学院,四川 宜宾
3四川建筑职业技术学院,四川 德阳

收稿日期:2021年6月7日;录用日期:2021年6月28日;发布日期:2021年7月12日

摘要
本文给出了一类二阶线性常微分方程边值问题的构造解法,运用此方法进一步求得了在相同边界条件下的非齐次零阶变型Bessel方程边值问题的解,并将该理论应用于具有源汇影响的变流率平面径向渗流力学问题中,结合Laplace变换法求得了该渗流力学模型在三种外边界条件下的连分式解式。研究表明,该方法可以方便、快捷地构造出此类边界条件下的统一解式,对同类边界条件下的扩散(热传导、渗流)方程求解具有重要意义。
关键词
非齐次Bessel方程,边值问题,渗流问题,构造解法
The Constructive Solution and Application of BVP for a Class of Non-Homogeneous Bessel Equations
Wei Li1, Songlin Zhang2, Haohan Liu3, Shunchu Li1
1School of Science, Xihua University, Chengdu Sichuan
2Yibin Vocational and Technical College, Yibin Sichuan
3Sichuan College of Architectural Technology, Deyang Sichuan
Received: Jun. 7th, 2021; accepted: Jun. 28th, 2021; published: Jul. 12th, 2021

ABSTRACT
This paper gives a constructive solution of a class of second order linear ordinary differential equation boundary value problem, by using this method, a non-homogeneous zero order modified Bessel equation BVP in the same boundary conditions is solved. Then the theory is also applied to the plane radial seepage mechanics with variable flow rate and source sink effect, combined with Laplace transform method, the continued fraction solutions of the seepage mechanics model under three kinds of external boundary conditions are obtained. The results show that this method can easily and quickly construct the unified solution under the same boundary conditions, which is of great significance for solving the diffusion (heat conduction, seepage) equation under the same boundary conditions.
Keywords:Non-Homogeneous Bessel Equation, Boundary Value Problem, Seepage Problem, Constructive Solution

Copyright © 2021 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
在解决数学物理问题如热的传导、浓度扩散以及工程中的流体渗流力学等问题中常常会遇到扩散方程,它们在数学本质上都是二阶抛物型微分方程,因此研究二阶微分方程的求解方法具有重要意义。
对于二阶线性齐次偏微分方程的解法已经非常成熟,常见的有分离变量法,是将偏微分方程分离为多个常微分方程分别求解,再根据线性方程叠加原理求得形式解;积分变换法是通过构造正交函数系求得积分变换对,将偏微分方程化为常微分方程,将常微分方程化为代数方程来求解 [1]。具有汇源影响的方程中通常会出现非齐次方程或非齐次边界条件,求解此类方程比较常用的是Green函数法,但需要借助分离变量法求得对应的齐次问题的解,从而构造相应的Green函数,然后将此Green函数与方程的非齐次项或非齐次边界作卷积运算求得解 [2],且运算过程较为繁琐。对非齐次方程的求解更为一般的有常数变易法、微分算子法、Laplace变换法、待定系数法等,虽解法各有优劣,但在很大程度上都需要求解常微分方程。一般的二阶常系数线性微分方程的求解归结为求取方程的特征值和特征函数 [3]。对特殊的变系数二阶常微分方程,如Bessel方程 [4]、Euler方程、Legendre方程等,其通解是由各方程对应的特殊函数所构成 [5]。在非稳态扩散(热传导、渗流)方程中,Bessel方程最为常见,求解其所构成的初边值问题是研究此类问题的关键。李顺初 [6] [7] [8] [9] 在求解二阶齐次线性微分方程(组)初边值问题的研究中发现该类问题的解式都具有相似的连分式结构,并在研究油气藏试井解释模型中 [10] [11],同样得到具有相似性的连分式解。进一步地,该研究团队又提出了求解二阶常微分方程边值问题的相似构造法 [12] [13] [14],并获得了丰硕的成果。
本文将进一步把该理论应用于求解二阶非齐次零阶变型Bessel方程的边值问题,探索该非齐次方程边值问题的构造解法,并将其应用于具有源汇影响的变流率渗流问题中,结合Laplace变换求得了模型的半解析解,应用数值反演技术可以满足工程需要。该研究表明此方法快捷有效、应用范围广,是对微分方程求解方法的拓展,对此类扩散方程初边值问题求解具有重要意义。
2. 二阶线性微分方程的构造解
引理1 如果二阶线性微分方程边值问题
(1)
(2)
(3)
(其中 均为已知的实常数,且 ;已知函数 )有唯一解,则其解可以表示为如下的连分式形式 [12]
(4)
其中
(5)
称为解的相似核函数。
假设 , 是(1)式方程的两个线性无关的解,构造以下二元函数
(6)
并记
(7)
(8)
(9)
称为相似核函数的生成函数。
引理2 在(3)式外边界条件 中,若 ,则外边界条件
变为第一类边界条件 ,相应的核函数为
(10)
在(3)式外边界条件 中,若 ,则外边界条件变为第二类边界条件 ,相应的核函数为
(11)
在边值问题(1)~(3)式的解(4)式中连分式结构中的第一个连分式有如下性质
(12)
此式反映了解在内边界处的本质性的特征,在渗流力学理论中起着十分重要的作用。
定理1 如果Bessel函数 是零阶齐次变型Bessel方程
(13)
的两个线性无关的解,则其通解为
(14)
则方程(13)式与边界条件(2) (3)式所构成的边值问题仍然具有形如(4)式的解式 [6],
其中的相似核函数形式也与(5)式完全相同,区别只在于二元生成函数
(15)
根据Bessel函数的微分性质有
(16)
(17)
(18)
这里
(19)
其中 是 阶变型Bessel函数。
利用上式得相似核函数
其中上标“*”表示由变型Bessel函数生成的函数。
定理2 对于非齐次零阶变型Bessel方程
(20)
采用常数变易法不难求得特解为(证明见附录)
(21)
则非齐次方程(20)式的通解为
(22)
则由非齐次零阶变型Bessel方程(20)式与边界条件(2) (3)式联立构成的边值问题的解为对应齐次方程边值问题的解与非齐次方程特解之和
(23)
3. 非稳态变流率渗流模型的构造解
将上述边值问题解的构造理论应用于带有源汇影响的非稳态变流率平面径向渗流模型可以直接构造得出模型的解。
无因次渗流方程
(24)
考虑井筒储集效应和表皮影响的内边界条件
(25)
(26)
初始条件 (27)
无因次外边界条件
(28)
(29)
(30)
其中: ——无因次井筒储集系数;
——表皮因子;
——无因次井源汇强度;
——无因次变流率;
无因次变量定义如下
将渗流问题(24)~(30)式作关于时间 的Laplace变换得以下二阶常微分非齐次方程边值问题
(31)
(32)
(33)
(34)
由线性方程叠加原理不难证明,方程(31)的解
(35)
其中 是方程
(36)
的解,因此渗流问题(31)~(34)式的求解可以转化为以下边值问题的求解,同时合并(32) (33)式有
(37)
(38)
(39)
只要令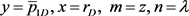 ,
,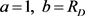 ,
,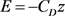 ,
,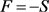 ,
,
则边值问题(37)~(39)式与(20)、(2)、(3)式所构成的边值问题完全等价,根据(23)式可得其解为
 (40)
(40)
根据(35)式,可得渗流问题(31)~(34)式的Laplace空间解
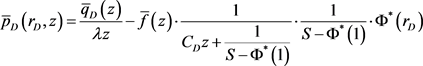 (41)
(41)
其中的相似核函数为
 (42)
(42)
由引理2中(10)式知当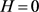 时,可得对应渗流模型定压外边界条件下的相似核函数
时,可得对应渗流模型定压外边界条件下的相似核函数
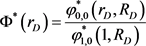 (43)
(43)
由(11)式知,当 时,可得对应渗流模型不渗透封闭外边界条件下的相似核函数
时,可得对应渗流模型不渗透封闭外边界条件下的相似核函数
 (44)
(44)
当渗流模型外边界无穷大时相似核函数变为
 (45)
(45)
只要将渗流模型不同外边界条件下对应的相似核函数(43)~(45)式代入(41)式即可得到该油藏模型在三种外边界条件下的统一连分式解。
由于对(41)式作Laplace逆变换较为困难,运用Stehfest数值反演技术结合计算机软件,可以获得实空间压力动态典型曲线,可以满足工程需要。
4. 结论
1) 本文提出的一类二阶线性常微分方程边值问题在三类外边界条件下具有统一的连分式形式解,并且内边界条件系数决定解的结构,外边界条件决定解的相似核函数;
2) 根据线性微分方程解的结构及叠加原理,求得了非齐次零阶变型Bessel方程边值问题的解式,其解可以根据相应的齐次变型Bessel方程边值问题的构造求得;
3) 多孔介质内流体的非稳态渗流方程、热传导方程以及扩散方程在本质上都可以归结为本文提出的非齐次零阶变型Bessel方程,他们在数学本质上是一致的。该研究是对二阶非齐次扩散方程求解方法的一种扩展,对求解此类方程具有重要意义。
基金项目
四川省教育厅项目(No. 15ZB0450、18ZB0439),教育部产学研合作办学项目(No. 201702028006),西华大学人才引进项目(No. Z201076),宜宾职业技术学院基金项目(No. YBZYSC20BK05)。
文章引用
李 伟,张松林,刘浩瀚,李顺初. 一类非齐次变型Bessel方程边值问题的构造解法及应用
The Constructive Solution and Application of BVP for a Class of Non-Homogeneous Bessel Equations[J]. 应用数学进展, 2021, 10(07): 2320-2329. https://doi.org/10.12677/AAM.2021.107242
参考文献
- 1. 谷超豪, 李大潜. 数学物理方程(第三版) [M]. 北京: 高等教育出版社, 2012.
- 2. 孔祥言. 高等渗流力学(第二版) [M]. 合肥: 中国科技大学出版社, 2010.
- 3. 王高雄, 周之铭, 朱思铭, 王寿松. 常微分方程(第四版) [M]. 北京: 高等教育出版社, 2020.
- 4. 常安定, 左大海. 非齐次贝塞尔方程的解[J]. 纺织高校基础科学学报, 2000, 13(3): 273-274.
- 5. 吴小庆. 数学物理方程及其应用[M]. 北京: 科学出版社, 2008.
- 6. 李顺初, 伊良忠, 郑鹏社. 微分方程定解问题解的相似结构[J]. 四川大学学报(自然科学版), 2006, 43(4): 933-934.
- 7. 贾闽惠, 李顺初. Bessel方程的边值问题解的相似结构[J]. 大学数学, 2005(5): 40-42.
- 8. Tian, J.D. and Li, S.C. (2004) The Formal Similarity of Solutions in the Laplace Space on the Class of Quasilinear Partial Differential Equation System. Mathematical Theory and Application, 24, 66-73.
- 9. 李顺初. 二阶齐次线性微分方程的边值问题的解的相似结构[J]. 西华大学学报: 自然科学版, 2009, 28(5): 40-41.
- 10. 李顺初, 郑鹏社, 张宇飞. 均质油气藏试井分析解的相似结构[J]. 纯粹数学与应用数学, 2006, 22(4): 459-463.
- 11. 李顺初, 郑鹏社, 张宇飞. 分形油藏试井分析解的相似结构[C]//资源、环境与渗流力学——第八届渗流力学学术讨论会论文集: 2005年卷. 北京: 中国科学技术出版社, 2005: 79-83.
- 12. 李顺初, 吴小庆. 二阶线性齐次方程两点边值问题的几个重要性质[J]. 西华大学学报(自然科学版), 2013, 32(1): 23-26.
- 13. Sheng, C.C., Zhao, J.Z., Li, Y.M. and Li, S.C. (2013) Similar Construction Method of Solution for Solving the Mathematical Model of Fractal Reservoir with Spherical Flow. Journal of Applied Mathematics, 2013, 211-244. https://doi.org/10.1155/2013/219218
- 14. Bai, L.X., Li, S.C., Gui, D.D., et al. (2014) Similar Structure Algorithm for Solving Boundary Value Problem of Differential Equations. Applied Mechanics and Materials, 574, 665-671. https://doi.org/10.4028/www.scientific.net/AMM.574.665
附录
关于定理2中非齐次零阶变型Bessel方程特解的求得证明如下
定理2中非齐次零阶变型Bessel方程
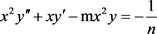 (A1)
(A1)
对应的齐次方程为
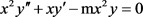 (A2)
(A2)
由定理(1)知方程通解为
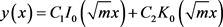 (A3)
(A3)
下面采用常数变易法求特解,假设非齐次方程(A1)式的通解为
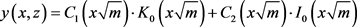 (A4)
(A4)
则 由以下方程组确定
由以下方程组确定
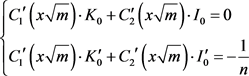 (A5)
(A5)
根据Bessel函数的性质
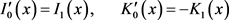
可得Wronski行列式

根据线性方程组的Cramer法则可得
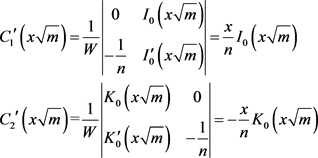 (A6)
(A6)
再根据Bessel函数的积分性质

得

若只求特解,则有
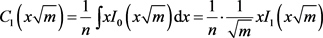 (A7)
(A7)
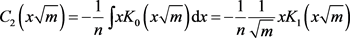 (A8)
(A8)
代入(A4)式可得方程(A1)的特解
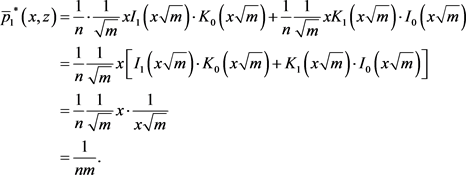 (A9)
(A9)