International Journal of Mechanics Research
Vol.
08
No.
02
(
2019
), Article ID:
30936
,
9
pages
10.12677/IJM.2019.82018
Compliance Calculation and Analysis of Half Right Circular Flexure Hinge
Yuemin Yu, Yuanzhu Ding, Liyan Yu, Fangfang Gai
College of Science, Heilongjiang University of Science & Technology, Harbin Heilongjiang

Received: Jun. 4th, 2019; accepted: Jun. 18th, 2019; published: Jun. 25th, 2019

ABSTRACT
The compliance calculation formula of half right circular flexure hinge was derived on the Castigliano’s theorem. The influence of geometric parameters on compliance is studied. The correctness of the formula was verified by adopting the finite element simulation software. The results show that the relative errors of the half right circular flexure hinge are all less than 10%; the theoretical analysis is in agreement with the simulation results, which verifies the correctness of the proposed formula. These results will play a key theoretical basis for the structural design of half right circular flexure hinge in practical applications.
Keywords:Half Right Circular Flexure Hinge, Compliance, Castigliano’s Theorem, Finite Element
单边直圆柔性铰链的柔度计算与分析
于月民,丁元柱,于丽艳,盖芳芳
黑龙江科技大学理学院,黑龙江 哈尔滨

收稿日期:2019年6月4日;录用日期:2019年6月18日;发布日期:2019年6月25日

摘 要
以卡式定理为理论基础,推导了单边直圆柔性铰链的柔度计算公式,分析了单边直圆柔性铰链的结构参数对其柔度性能的影响。利用有限元方法对单边直圆柔性铰链的柔度计算公式进行校验,结果表明:公式计算值相对误差均小于10%,理论分析与仿真结果基本吻合,验证了单边直圆柔性铰链柔度计算公式的正确性。本文的研究内容为单边直圆柔性铰链的工程设计提供理论基础。
关键词 :单边直圆柔性铰链,柔度,卡氏定理,有限元

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
柔性铰链是一种体积小、结构紧凑且灵敏度高的传动结构,在高精度传动的场合被广泛应用 [1] [2] [3] 。柔度是评价柔性铰链动力学性能的重要指标之一,柔度能反映出载荷与变形间的解析关系。Paros和Weisbord利用积分法得到了圆弧形柔性铰链的柔度计算公式,并在铰链半径远远大于铰链最小厚度的条件下,得到了圆弧形柔性铰链柔度的近似解 [4] 。Smith研究了一种叶状形的柔性铰链,并把它应用到快速响应的高精度运动控制的柔性机构中 [5] 。Lobonitu等推导出了导角形柔性铰链的刚度公式和转动精度公式,并利用有限元方法和实验进行了验证 [6] 。Lobontiu基于能量原理研究了双轴柔性铰链的旋转能力和旋转精度 [7] 。陈贵敏引入椭圆离心角作为积分变量,推导了椭圆柔性铰链的柔度计算公式 [8] 。杨春辉等推导了直梁型柔性球铰和圆弧形柔性球铰柔度的解析公式 [9] [10] 。邱丽芳等人分析了表示柔性铰链运动性能的柔度矩阵,以柔性铰链的结构参数为设计变量,建立了多目标优化模型 [11] 。姚建涛等通过引入比例系数,得到了直圆柔性球铰柔度矩阵各子元素的解析柔度计算公式 [12] 。陈应舒等对曲梁柔性铰链的柔度以及精度进行了分析 [13] 。单边柔性铰链的结构更为紧凑,在空间受限的柔性机构中有着更广泛的应用前景 [14] [15] 。本文针对单边直圆柔性铰链,基于线弹性和小变形假设理论,利用能量法提出单边直圆柔性铰链的柔度解析计算公式,用有限元验证柔度公式的正确性,并对单边直圆柔性铰链的结构参数对其柔性能的影响规律进行深入研究。
2. 单边直圆柔性铰链柔度模型
单边直圆柔性铰链的结构见图1所示,R为柔性铰链的切割半径,t为柔性铰链的最小厚度,柔性铰链的宽度为w。单边直圆柔性铰链受力如图2所示,柔性铰链左端固定,右端为自由端,受到水平方向力Fx,竖直方向力Fy和力偶Mz作用。

Figure 1. Half right circular flexure hinge
图1. 单边直圆柔性铰链

Figure 2. Loads of half right circular flexure hinge
图2. 单边直圆柔性铰链受力分析
基于线弹性和小变形假设理论,在载荷作用下的单边直圆柔性铰链自由端的位移–载荷方程为:
(1)
式中: 为单边直圆柔性铰链自由端沿x、y的线位移和绕z的角位移。 为作用于单边直圆柔性铰链自由端的载荷,下标x,y,z表示载荷的矢量方向, 为单边直圆柔性铰链的柔度矩阵。
单边直圆柔性铰链自由端受水平方向力Fx,竖直方向力Fy和力偶Mz共同作用时,柔性铰链的变形能由轴向拉伸变形能和弯曲变形能组成。
(2)
式中:E是材料的拉压弹性模量,A(x)是柔性铰链横截面面积,I(x)是柔性铰链横截面的惯性矩。
3. 单边直圆柔性铰链柔度计算
任意x处铰链的厚度:
, (3)
任意x与角度φ的关系
, (4)
任意横截面的面积:
(5)
任意横截面的惯性矩为:
(6)
单边直圆柔性铰链在Fx作用下,沿x轴产生的线位移Δx为:
(7)
由式(7)可知,单边直圆柔性铰链受沿x向的力Fx作用时,自由端沿x方向的线变形柔度C11为:
(8)
式中: 。
单边直圆柔性铰链在Fy和Mz作用下,产生沿y方向的线性位移Δy为:
(9)
由式(9)可知,单边直圆柔性铰链受沿y向的力Fy作用时,自由端沿y方向的线变形柔度C22为:
(10)
单边直圆柔性铰链受沿z向的力偶Mz作用时,自由端沿y方向的线变形柔度C23为:
(11)
单边直圆柔性铰链在Fy和Mz作用下,产生沿z方向角位移θZ为:
(12)
由式(12)可知,单边直圆柔性铰链受沿z向的力偶Mz作用时,自由端沿z方向的角变形柔度C33为:
(13)
单边直圆柔性铰链受沿y向的力Fy作用时,自由端沿z方向的角变形柔度C32为:
(14)
4. 柔度的实例计算及有限元验证
4.1. 结构参数对柔度性能影响
通过分析柔性铰链的柔度公式(8)、(10)、(11)和(13)可知:柔度均与弹性模量E和铰链宽度w成反比。当单边直圆柔性铰链的弹性模量E和铰链宽度w确定时,为进一步分析柔性铰链的结构参数t和R对其柔度性能的影响,利用MATLAB编写程序计算不同结构参数t和R下的单边直圆柔性铰链柔度,利用Origin软件绘制单边直圆柔性铰链的柔度与结构参数t和R的关系曲线,见图3~10所示。

Figure 3. The relation between C11 and t
图3. C11随参数t的变化
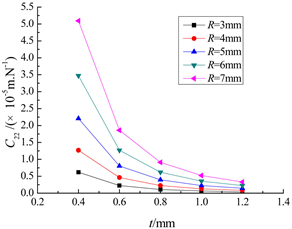
Figure 4. The relation between C22 and t
图4. C22随参数t的变化

Figure 5. The relation between C23 and t
图5. C23随参数t的变化

Figure 6. The relation between C33 and t
图6. C33随参数t的变化

Figure 7. The relation between C11 and R
图7. C11随参数R的变化
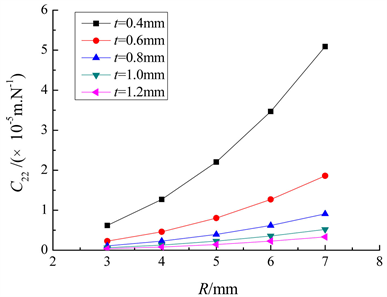
Figure 8. The relation between the C22 and R
图8. C22随参数R的变化

Figure 9. The relation between C23 and R
图9. C23随参数R的变化
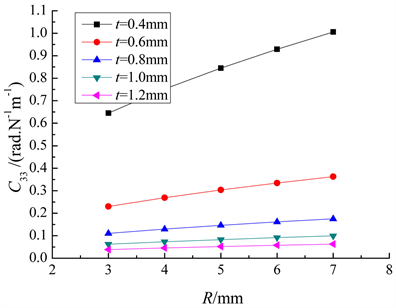
Figure 10. The relation between C33 and R
图10. C33随参数R的变化
图3~6给出了不同切割半径R下,单边直圆柔性铰链的柔度与铰链最小厚度t之间的关系曲线,通过观察可以发现,柔度与最小厚度t呈非线性递减关系,切割半径R越大,柔度的非线性关系程度的越大。图7~10给出了不同铰链最小厚度t下,单边直圆柔性铰链的柔度与切割半径R之间的关系曲线,通过观察可以发现,柔度与切割半径R呈非线性递增关系,铰链最小厚度t越小,柔度的非线性关系程度的越大。
4.2. 有限元分析
利用ANSYS软件仿真计算,验证上述单边直圆柔性铰链柔度解析计算公式的求解精度。单边直圆柔性铰链的结构参数为:截面宽度w = 4 mm,铰链最小厚度t分别取0.4 mm,0.6 mm,0.8 mm,1.0 mm,1.2 mm,柔性铰链切割半径R = 5 mm。对单边直圆柔性铰链自由端参考点分别施加沿x向、y向和z向的单位载荷,从而得到单边直圆柔性铰链的柔度,单边直圆柔性铰链的材料参数见表1所示,有限元分析的结果和柔度公式计算结果见表2所示。
Table 1. Material parameters of half right circular flexure hinge
表1. 单边直圆柔性铰链的材料参数
Table 2. The results contrast between compliance computation and finite element analysis
表2. 解析计算结果与有限元分析结果对比
由表2中数据可知,由于ANSYS网格划分精度以及加载位置的偏差,导致计算结果出现了误差。有限元结果和柔度公式计算结果的误差在10%以内,公式所得的结果与有限元分析结果基本一致,从而验证了单边直圆柔性铰链柔度计算公式的正确性。
5. 结论
本文对单边直圆柔性铰链的柔度性能进行了分析,利用卡氏二定理推导出了单边直圆柔性铰链的柔度解析式,分析了结构参数对单边直圆柔性铰链柔度性能的影响关系,并用有限元的方法对其柔度公式进行了验证,和有限元法相比公式计算值的相对误差均在10%以内,公式所得的结果与有限元分析结果基本一致,从而验证了单边直圆柔性铰链柔度计算公式的正确性,为单边直圆柔性铰链的工程设计和计算提供了有价值的参考。
基金项目
黑龙江省自然科学基金(E2015032)。
文章引用
于月民,丁元柱,于丽艳,盖芳芳. 单边直圆柔性铰链的柔度计算与分析
Compliance Calculation and Analysis of Half Right Circular Flexure Hinge[J]. 力学研究, 2019, 08(02): 156-164. https://doi.org/10.12677/IJM.2019.82018
参考文献
- 1. 卢清华, 黄世乾. 一种3自由度精密微定位平台的设计与分析[J]. 机械设计与研究, 2014, 30(5): 56-59.
- 2. 李春霞, 赖磊捷, 朱利民. 三自由度θX θY Z柔性机构的柔度分析与计算工[J]. 工程力学, 2014, 31(8): 204-222.
- 3. 崔玉国, 王子宾, 马剑强, 等. 四自由度压电微夹钳的设计[J]. 机械工程学报, 2017, 53(23): 165-173.
- 4. Paros, J. (1965) How to Design Flexure Hinges. Journal of Mechanical Design, 37, 151-156.
- 5. Smith, T.S. and Badami, V.G. (1997) Elliptical Flexure Hinge. Review of Scientific Instruments, 68, 1474-1483. https://doi.org/10.1063/1.1147635
- 6. Lobontiu, N. and Paine, J.S. (2001) Corner-Filleted Flexure Hinges. Journal of Mechanical Design, 123, 346-352. https://doi.org/10.1115/1.1372190
- 7. Lobontiu, N. (2002) Design of Circular Cross-Section Corner-Filleted Flexure Hinges for Three-Dimensional Compliant. Journal of Mechanical Design, 124, 479-484. https://doi.org/10.1115/1.1480022
- 8. 陈贵敏, 刘小院, 贾建援. 椭圆柔性铰链的柔度计算[J]. 机械工程学报, 2006, 23(s1): 111-115.
- 9. 杨春辉. 倒圆角直梁型柔性球铰柔度计算与分析[J]. 机床与液压, 2013(3): 55-58.
- 10. 杨春辉, 刘平安. 圆弧形柔性球铰柔度设计计算[J]. 工程设计学报, 2014, 21(4): 389-404.
- 11. 邱丽芳, 南铁玲, 翁海珊. 柔性铰链运动性能多目标优化设计[J]. 工程科学学报, 2008, 30(2): 189-192.
- 12. 姚建涛, 李立建, 杨维, 等. 直圆柔性球铰柔度矩阵的解析计算[J]. 光学精密工程, 2014, 2(7): 1857-1863.
- 13. 陈应舒, 朱淳逸. 曲梁柔性铰链性能分析及应用机构设计[J]. 机械设计与制造, 2018(11): 183-185.
- 14. 张志杰, 袁怡宝, 于汶. 单边椭圆柔性铰链的计算与性能分析[J]. 机械设计与研究, 2007, 23(1): 50-53.
- 15. 张志杰, 袁怡宝. 单边导角形柔性铰链的计算与性能分析[J]. 光学精密工程, 2007, 15(3): 384-389.
