Dynamical Systems and Control
Vol.
08
No.
02
(
2019
), Article ID:
29519
,
8
pages
10.12677/DSC.2019.82012
Optimal Decoupling Control of Linear Interference Systems
Zetao Chen, Chaoyong Jin
School of Applied Mathematics, Guangdong University of Technology, Guangzhou Guangdong

Received: Mar. 8th, 2019; accepted: Mar. 19th, 2019; published: Mar. 29th, 2019

ABSTRACT
For linear multivariable system with interference, this paper combines system decoupling control and optimal tracking control to achieve system decoupling while allowing the system to optimize a certain performance index and realize the tracking of the reference output system. In order to help with decoupling, the differential equation on state is transformed into that on output and a controller is designed. The optimal tracking is performed on the reference input introduced in the decoupling process to obtain the optimal tracking control law. Finally, the decoupling control is combined with the optimal tracking control getting the optimal decoupling control law. The method realizes the decoupling of the victim system and the tracking of the output, and optimizes a certain performance index. The superiority of the method can be verified by simulation results.
Keywords:Decoupling Control, Optimal Tracking Control, Interference System
线性干扰系统的最优解耦控制
陈泽涛,金朝永
广东工业大学应用数学学院,广东 广州

收稿日期:2019年3月8日;录用日期:2019年3月19日;发布日期:2019年3月29日

摘 要
对于带干扰的线性多变量系统,本文把系统解耦控制以及最优跟踪控制结合在一起,在实现了系统解耦的同时,使系统达到某项性能指标最优,并对参考输出进行跟踪。首先,我们把系统关于状态的微分方程转化成关于输出的方程,并设计控制器进行解耦。然后对解耦过程中引入的参考输入进行最优跟踪控制,并求取最优跟踪控制律。最后把解耦控制与最优跟踪控制相结合一起,得到最优解耦控制律。该方法实现了受扰系统的解耦以及对输出的跟踪,并使得某项性能指标最优。由仿真结果可验证该方法的优越性。
关键词 :解耦控制,最优跟踪控制,干扰系统

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
多输入多输出系统广泛应用于现代工业,然而大部分系统都存在着各种输入输出变量之间的耦合特性。耦合导致系统的控制效果不理想,性能也比较差。所以,如何解决或者降低系统之间的耦合度也成为控制理论一个重要的研究课题。
上世纪50年代,Roksenbom和Hood [1] 在报告中提出了多变量解耦问题,他们是最先把不相关思想和矩阵分析应用到系统解耦的人。1964,Gilbert E.G.提出Morgan [2] 解耦问题,Morgan解耦问题的核心思想在于寻找合适的控制规律,解决输入及输出的交叉耦合,使得每个输出变量均由一个输入变量决定。其缺点也很明显,由于是精确解耦,所以系统的任意变动都可以导致原先的解耦遭到破坏。随着系统的复杂化以及系统之间存在的更多难以控制的因素,工业上对解耦的要求也变得更高,解耦系统的设计难度也更大,解耦方法也随之复杂、全面。
文献 [3] 中介绍了解耦的发展历史以及一些常用的解耦方法。自适应解耦是将被控系统控制以及系统辨识结合起来,使控制器设计与闭环解耦相结合的在线解耦控制。文献 [4] 采用自校正前馈控制的方法对耦合进行静态补偿最终实现解耦。文献 [5] 采用最小方差控制律对系统耦合进行抑制交联,从而达到解耦目的。文献 [6] 也类似地采用最小方差控制律进行解耦。文献 [7] 设计了内模控制器,并将解耦控制与内模控制器等效成一个单参数的PID控制器,以达到解耦的目的。而文献 [8] 将干扰观测器和解耦控制器相结合,实现解耦的目的的同时,使得干扰得到有效的抑制。神经网络解耦控制主要是针对一些非线性的系统,即在复杂非线性系统前添加神经网络解耦控制器,并通过学习训练达到消除耦合的目的,是把现代智能以及解耦控制结合在一起的有效方法。文献 [9] 联合神经网络以及广义预测解耦控制方法,对系统进行解耦,文献 [10] 基于神经网络的基础上,降低了解耦矩阵的复杂性,实现解耦的同时,提高了系统的响应能力。模糊解耦控制不拘于传统的数学模型,运用模糊规则对系统进行解耦。文献 [11] 将模糊智能算法与解耦控制结合,设计PID控制对非线性系统进行解耦。文献 [12] 同时利用模糊控制以及神经网络,提高了解耦的控制精度。结合国内外的解耦控制方法以及上述的方法,我们可以看到,虽然这些方法可以实现工业上的解耦过程,但是在越来越复杂的工业过程中,无法兼顾系统日益剧增的性能要求。现代工业不仅考虑到单纯对系统实现解耦,往往也考虑到系统性能,为达到复杂工业的整体优化问题。工业设计过程中经常需要对控制对象进行解耦的同时,对参考系统有良好的跟踪能力。文献 [13] 提出了线性系统的最优解耦控制方法,但是未考虑到现实工业过程的干扰问题,适用性不是很强。针对这个问题,本文提出了具有干扰的线性系统的最优解耦方法。首先将受扰系统转化成输出模型,再把输出模型的内部矩阵分成对角矩阵以及对角线为0的两个矩阵相加,然后设计解耦控制器,将系统进行开环解耦。我们为解耦后系统设计最优跟踪策略,使解耦后系统达到性能指标最优。
2. 问题描述
如下线性多变量干扰系统为我们研究对象:
(1)
其中 为状态向量, 为控制向量, 为干扰向量, 为输出向量,其中 均为时不变矩阵。
系统持续扰动可由以下系统描述:
(2)
其中,
为干扰系统的状态向量,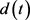 为干扰系统的输出向量。干扰系统是完全可观测系统,并且
为行满秩矩阵。
为干扰系统的输出向量。干扰系统是完全可观测系统,并且
为行满秩矩阵。
针对以上系统,我们需要求取一个最优控制律 ,实现干扰系统解耦的同时,使得系统输出 在最大程度上跟踪给定参考输出 的变化,其中参考输出 由下面动态系统产生
(3)
其中 表示参考输出系统的 维状态向量, 表示受扰线性系统的 维参考输出向量。参考输出系统是完全可观测的。
3. 解耦控制
对于上述解耦系统(1),我们把该其由状态方程转化成如下关于输出的微分方程
(4)
其中 ,然后,将系统中第 个通道输入 对第 个通道 之间的耦合看成可测干扰,采用反馈方法消除系统 中第 个输出变量对第 个输出变量的影响。可以把(4)式转化为
(5)
其中
为对角矩阵,其对角线上的元素为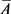 主对角线上的元素,其他元素都为零,
,
为主对角线上为零的矩阵,我们可以定义其为不同变量间的耦合影响;同理,
为对角矩阵,
,我们定义其为同通道间的耦合影响。将矩阵转化成以上形式后,引入参考输入变量
设计如下解耦控制器
主对角线上的元素,其他元素都为零,
,
为主对角线上为零的矩阵,我们可以定义其为不同变量间的耦合影响;同理,
为对角矩阵,
,我们定义其为同通道间的耦合影响。将矩阵转化成以上形式后,引入参考输入变量
设计如下解耦控制器
(6)
其中,所设计的 为对角矩阵, 为主对角线元素均为零的矩阵, 可逆。现在用 左乘式子(5),可得
 (7)
(7)
左乘式子(7)可得
(8)
并用 左乘(6)可得
(9)
结合式子(8)与(9)可得
(10)
由式子可知,为实现输入输出解耦,应该选择适当的 使得如下等式成立
(11)
则(10)可以转化成
(12)
由于矩阵 以及 均为对角矩阵,因此(12)式实现了辅助输入 和系统输出 之间的解耦。
4. 最优跟踪控制
为方便进行最优跟踪控制器的设计,定义 则模型(12)式可简化成以下方程如下方程
(13)
针对以上系统(13),我们设计参考输入 ,使得以下性能指标
(14)
达到最优。其中 为跟踪误差, ,均为对称正定的加权矩阵。根据最优跟踪控制策略,我们的目的是找到最优控制律 ,使得性能指标(14)能够取得极小值。
定理1 [14] [15]
对带有持续扰动的线型多变量系统,其在有限时域线性二次型性能指标(14)下的最优输出跟踪控制律为
(15)
式中 是下述 矩阵微分方程的唯一解
(16)
是下述 矩阵微分方程的唯一解
(17)
是下述 矩阵微分方程的唯一解
(18)
结合式(6)和(15),我们可以得到系统的最优解耦控制律为
(19)
5. 仿真
为验证所提出方法的有效性,我们对如下系统进行了仿真实验:
(20)
上述系统中, 为受扰线性系统的二维状态向量 为受扰线性系统的二维输入向量, 为系统的二维输出向量, 为系统的二维干扰信号。系统的内部矩阵,控制输入矩阵,外部干扰矩阵已经输出矩阵分别为
其中外部持续扰动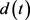 的动态特性可以由以下外部系统描述出来:
的动态特性可以由以下外部系统描述出来:
上述干扰外系统中, 为干扰外系统的二维状态向量。 和 为常量矩阵,在此,我们选择常量矩阵为
的干扰外系统,该干扰系统完全可观测。
为受扰系统的参考输出,该参考输出的动态特性描述如下:
其中, 为参考输入系统的二维状态向量。
为参考输入系统的二维状态向量。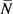 和
N 为常量矩阵,我们选择常量矩阵分别为
和
N 为常量矩阵,我们选择常量矩阵分别为
的参考输出系统。
现在我们对系统(20)进行解耦,根据等式(11)我们选择加权矩阵
由此我们可知
解耦后可得如下模型:
(21)
模型(20)的最优性能指标如下
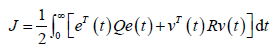 (22)
(22)
针对性能指标(22),我们选取
解代数黎卡提方程(16)可得
应用MTALAB求解方程(17),(18)可得
仿真结果如下图,如图1分别为最优解耦跟踪控制的输出 以及其跟踪变量 ,图2分别为系统输出 以及 。
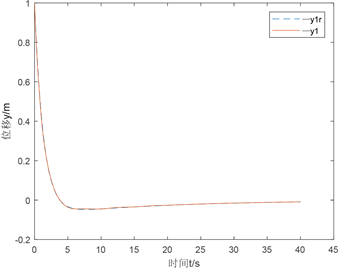
Figure 1. Output y1 and tracking variables y1r for optimal decoupling control methods
图1. 最优解耦控制方法输出y1以及跟踪变量y1r
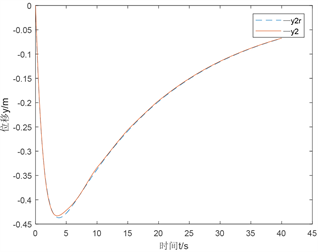
Figure 2. Output y2 and tracking variables y2r for optimal decoupling control methods
图2. 最优解耦控制方法输出y2以及跟踪变量y2r
同时,我们把直接给出系统进行最优跟踪后的仿真图,如图3,为最优跟踪方法的输出 以及跟踪变量 。图4为输出 以及跟踪变量 。
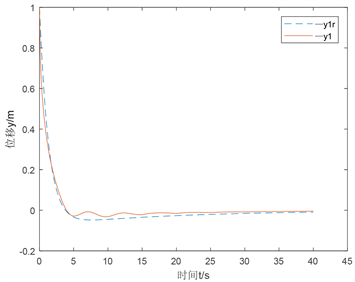
Figure 3. Output y1 and tracking variables y1r for optimal tracking methods
图3. 最优跟踪方法的输出y1以及跟踪变量y1r
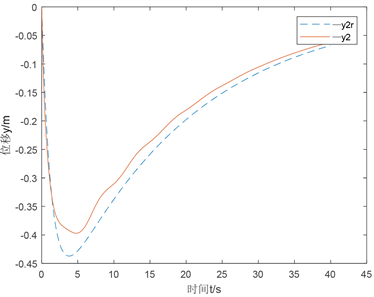
Figure 4. Output y2 and tracking variables y2r for optimal tracking methods
图4. 最优跟踪方法输出y2以及跟踪变量y2r
6. 结论
本文根据带干扰的连续时间线性系统(输入及输出维数相同),提出了一类由开环解耦控制以及最优跟踪控制结合在一起的最优解耦方法,实现了对干扰系统的解耦以及跟踪,并使得其某项性能指标达到最优。通过仿真,我们也可以看到该方法明显优于经典方法。
文章引用
陈泽涛,金朝永. 线性干扰系统的最优解耦控制
Optimal Decoupling Control of Linear Interference Systems[J]. 动力系统与控制, 2019, 08(02): 106-113. https://doi.org/10.12677/DSC.2019.82012
参考文献
- 1. Boksenboom, A.S. and Hood, R. (1949) General Algebraic Method Applied to Control Analysis of Complex Engine Types. National Advisory Committee for Aeronautics, Washington DC.
- 2. Morgan, B.S. (1964) The Synthesis of Linear Multivariable Systems by State Variable Feedback. IEEE Transactions on Automatic Control, 9, 404-411.
- 3. 桑保华, 薛晓中. 多变量解耦控制方法[J]. 火力与指挥控制, 2007, 32(11): 1297-1300.
- 4. Chai, T.Y., Lang, S.J. and Gu, X.Y. (1985) A Generalized Self-Tuning Feed-Forward Controller and Multivariable Application. Proceedings of 24th IEEE Conference on Decision and Control, Fort Lauderdale, 11-13 December 1985, 862-867.
- 5. Koivo, H.N. (1980) A Multivariable Self-Tuning Controller. Automatica, 16, 315-366.
https://doi.org/10.1016/0005-1098(80)90020-5 - 6. 柴天佑. 多变量间接自适应解耦控制算法[J]. 自动化学报, 1991, 17(5): 51-54.
- 7. 李玉霞, 黄小莉, 滕银银. 多变量解耦内模控制系统设计与仿真[J]. 西华大学学报, 2018, 37(3): 96-100.
- 8. 荣志刚, 门以双, 雷阳. 基于干扰观测器的解耦控制算法[J]. 信息技术, 2016(11): 164-167.
- 9. 舒迪前, 等. 多变量神经网络解耦广义预测控制及其应用[J]. 电气传动, 1996(4): 44-45.
- 10. 宋家康, 彭勇刚, 王晓明, 年珩. 基于神经网络的三端口DC-DC变换器解耦控制策略[J]. 电工电能新技术, 2019, 38(2): 20-26.
- 11. 徐江红, 王志伟. 基于模糊PID控制器的永磁同步电机逆系统解耦控制研究[J]. 科技与创新, 2018(19): 42-45.
- 12. 石书培, 褚建新, 周贤文. 基于神经网络补偿的温湿度试验箱模糊解耦控制[J]. 工业仪表与自动化装置, 2018(5): 67-84.
- 13. 富月, 李婧怡. 线性多变量系统有限时间最优解耦控制[J]. 控制与决策, 2016, 31(12): 2271-2274.
- 14. 张彬彬. 受扰系统最优跟踪控制方法研究[D]. 哈尔滨: 哈尔滨工业大学, 2014.
- 15. 刘蕾, 张国山. 基于动态补偿的线性系统最优干扰抑制[J]. 控制理论与应用, 2013, 30(7): 808-814.