Advances in Energy and Power Engineering
Vol.06 No.01(2018), Article ID:23853,10
pages
10.12677/AEPE.2018.61008
Improved Control Strategy of Optimization Operation of Transformer Bank
Liang Zhang1, Maoqun Zhang1, Dengming Chen1, Hao Zhang1, Jianyuan Wang2, Haitao Shi2
1Mentougou Power Supply Company of State Grid, Beijing Electric Power Corporation, Beijing
2Northeast Electric Power University, Jilin Jilin

Received: Feb. 6th, 2018; accepted: Feb. 20th, 2018; published: Feb. 27th, 2018

ABSTRACT
Boundary division method is the most commonly used transformer economic analysis method, the key is the critical load value. However, the critical load value is only a point value; the actual load is real-time changes, which will inevitably lead to frequent switching of the transformer. In view of this problem, this paper proposes a combination of critical point division and time division of the transformer economic operation control strategy, both to reduce the transformer loss and reduce the number of transformer switching, to achieve the economic operation of the transformer. Taking two transformers as an example, the advantages and disadvantages of this method are verified by analyzing and comparing the loss and switching times of different switching strategies.
Keywords:Transformer, Optimal Combination, Critical Load, Time Division Method
改进的变压器组优化运行控制策略
张靓1,张茂群1,陈登明1,章昊1,王建元2,史海涛2
1国网北京门头沟供电公司,北京
2东北电力大学,吉林 吉林
收稿日期:2018年2月6日;录用日期:2018年2月20日;发布日期:2018年2月27日

摘 要
临界点划分法是最常用的变压器经济运行分析方法,其关键是临界负荷值,然而临界负荷值只是一个点值,实际负荷是实时变化的,这样必然会造成变压器的频繁投切,针对这个问题,本文提出临界点划分法和时段划分法相结合的变压器经济运行控制策略,既减小变压器损耗又减少变压器的投切次数,实现变压器的经济运行。以两台变压器为例,通过分析比较不同投切策略的损耗和投切次数,验证本方法的优越性。
关键词 :变压器,优化组合,临界负荷,时段划分法

Copyright © 2018 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
所谓变压器经济运行,实质上就是通过合理安排变压器的运行方式最大幅度的降低变压器的损耗,提高变压器运行效率,但是此运行方式必须能确保电网的安全和可靠运行,也能满足用户对电能的需求量 [1] 。变压器经济运行的关键就是减少变压器的损耗,变压器的损耗主要是空载时由漏磁损耗和励磁电流产生的铁损和有负载时由负载电流在变压器线圈电阻上产生的铜损组成 [2] 。
变压器经济运行的节电技术长期以来备受重视,国内外的许多学者对此都进行了大量的研究,包括理论分析和各种实验,并且有大量的论文发表和专注出版。在这个知识经济的时代,人们不断的运用知识经济和科学技术在电力行业更新陈旧观念,来大幅度地挖掘节电潜力,提高经济效益。一直以来传统的耗能设备及理论误区并没有带来很好的经济效益,而是带来了不少的经济损失,还阻碍了设备的技术进步。所以对于经济运行的理论,很多的国内外学者们在不断的创新改进,进行着大量的研究。
我国在二十世纪中期的时候也对变压器经济运行做了相关的规定,而且当时对变压器的理论和实践的研究都有了一定的成绩。并且在二十世纪末的时候,国家技术监督局颁布了《工矿企业电力变压器经济运行导则》,该导则对变压器的经济运行具有非常重要的指导意义,而且对变压器优化运行的各个方面做了详尽的规定。我国著名专家胡景生更是在变压器经济运行方面有着突出贡献,他对变压器的经济运行做了全面的理论分析,包括变压器经济运行的相同及不同容量和台数的变压器的选择问题,以及对变压器经济运行区间划分和变压器的并分列运行的临界负荷的计算等,并且成立了专门的优化运行研究所,对优化运行进行理论分析和实验仿真,并整理成书籍和论文,在变压器经济运行方面贡献了巨大力量。目前我国变压器经济运行由于各个用电部门的重视和日益提高的技术支持,其效果已经初步显现出来 [3] 。文献 [4] 从理论上分析计算了配电变压器的综合损耗率及投资运行费用,并以此为依据分别考虑网损和综合考虑网损、投资费用两种情况,分析变压器的经济运行区间。文献 [5] 配电变压器经济运行模式的探讨中通过计算分析常用的S7、S9、S11系列配电变压器的经济运行模式,得出结论:变压器的负荷率越接近其经济负载系数,其运行越经济;越节能的变压器经济负载系数越低,经济运行区间也就越宽。文献 [6] 针对变压器和导线的选择配置,分析其技术经济运行区域,据此可评价配电网变压器和线路配置情况,为降损改造提供决策依据,这对配电网的经济运行有重要意义。文献 [7] 抽样统计了目前配电变压器负载运行情况,对提高载容率的措施进行了探讨。文献 [8] 该学位论文对配电网变压器经济运行区间的划分方法作了比较全面的研究和介绍,并提出了“处理负荷曲线与临界划分点法相结合”这一创新内容。文献 [9] 结合现行电价分析变压器的经济运行。文献 [10] 采用禁忌搜索算法求解变压器经济运行优化模型,适用于地区电网的变压器经济运行的整体优化。文献 [11] 研究负荷增长情况下配电变压器额定容量的选择从而构建最优的选择模型。
为了解决变压器频繁投切问题,本文采用了临界点划分法和时段划分法相结合的新的变压器组经济运行方式。通过算例仿真分析,改进的变压器组经济运行分析方法不仅降低了变压器的损耗,而且有效控制了变压器的开关次数,验证了该方法的有效性。
2. 临界点划分法
有两台变压器A和B,它们的容量相同,通过以上的理论研究可知,这两台变压器可以有两种运行方式,即A(或B)单独运行和A、B两台变压器共同运行。在这两种方式下其综合功率损耗和的计算如式分别如式(1)和(2)所示。
(1)
(2)
为了求出单台和两台运行的临界负载功率,需要使并且要联立式(1)和(2),解方程组能够求出如式子(3)。
(3)
把变压器在不同方式下产生的损耗和负载的关系通过图像表现出来,可以更加清楚地理解临界负载的意义。绘制成的曲线如图1所示,临界负载就是图中两条曲线的交点横坐标,并且从中可以发现临界负载和变压器容量SNi存在某种位置关系。
在 情况下可以直接根据变压器经济运行的临界负载功率将其分为两种方式,即当 时,由变压器A单独供电;当 时,由变压器A和B一起供电。

Figure 1. The relationship between transformer loss and load
图1. 变压器损耗和负载的关系曲线
3. 时段划分法
时段划分法是将城市小区的负荷预测曲线人为的处理为有规律的曲线,在处理后的负荷曲线上划分运行区间,每个运行区间对应相应的运行方式,并且这种运行方式不随负荷的变化随意改变 [12] 。时段划分法实现的前提是要能取得未来一段时间的负荷预测数据,然后通过对负荷预测数据曲线的处理,降低变压器经济运行的频繁投切。
时段划分法一般是对未来一天的负荷预测曲线按照一定的规则简化处理,在处理后的曲线上形成高峰、低谷、腰值3个分段。
首先需要得到所研究对象的短期负荷预测数据。假定1天按时间段平均采24个负荷预测值,将它们组成数列 。然后按如下规则进行处理:
1、若 ,则规定A的值为1,表示此段时间内负荷处于上升状态。
2、若 ,则规定A的值为0,表示此段时间内负荷处于不变状态。
3、若 ,则规定A为值为−1,表示此段时间内负荷处于下降状态。
按照这一规则处理完毕将得到1、0、−1组成的一组数列即 ,由此数列来表示负荷的变化。
以某小区某天负荷变化为例,根据其负荷预测值得到其负荷预测曲线如图2所示,按上述规则对图2处理之后得到负荷初步划分情况如图3所示。
观察图3可以发现还存在少量负荷波动,为处理这些波动制定规则如下:
1、若 且 ,则规定 的值和 的值相等。
2、若 ,则规定 的值和 、 的值相等。
按照新的规则处理完这些波动后,可以得到比较理想的负荷划分情况,如图4所示。
以由图4负荷最终划分情况可以看出全天的负荷被划分为三个阶段,分别为负荷上升阶段(6~22),负荷保持阶段(1~5),负荷下降阶段(23~24)。根据实际负荷的发展趋势来决定是否要改变运行方式。
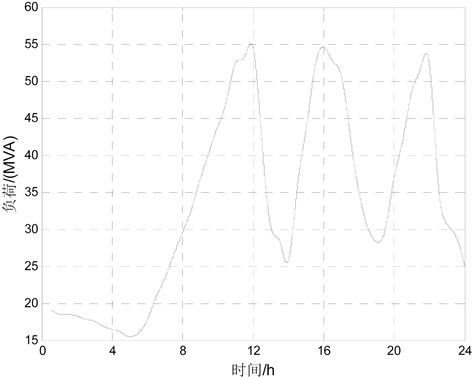
Figure 2. Load forecasting curve
图2. 变压器损耗和负载的关系曲线

Figure 3. The initial division of the load situation
图3. 负荷初步划分情况
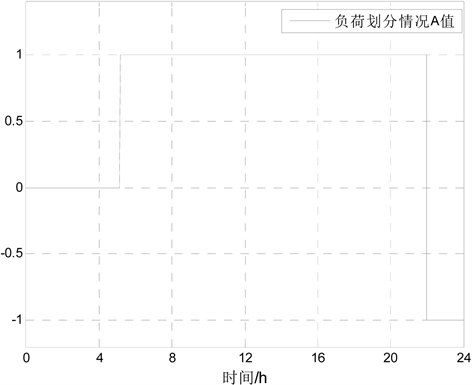
Figure 4. The final division of the load
图4. 负荷最终划分情况
基于上述方法处理负荷,变压器每天的投切次数将大幅减少,长期运行有利于减小变压器投切对开关机械强度和绝缘强度的影响。
4. 改进的变压器经济运行投切策略分析
4.1. 改进的变压器经济运行理论分析
前面分析变压器经济运行方式主要是利用临界点划分法求出不同运行方式之间的临界负荷值,通过比较实际负荷值和临界负荷值的大小决定变压器的投切,从而使变压器一直处于最经济的运行方式下。这种方法可以有效的降低变压器损耗,是最基本的也是比较常用的研究方法,但是此种方法最大的缺点就是需要频繁的开关变压器,所以在实际中存在不可操作性,为了更加有效的解决这个问题,本文采用临界点划分法与时段划分法相结合的分析方法。
1、通过对变压器经济运行方式的分析,利用临界点划分法计算公式求出不同运行方式的临界负荷值。
2、进行负荷预测,得到预测日24时段的负荷值,并通过时段划分法对曲线进行简化处理,得到只有一个波峰的矩形曲线。
3、为了改善临界点划分法带来的频繁投切问题,改进的变压器经济运行投切策略将时段划分法与之相结合,这样不只减少了变压器的投切次数,同时也降低了变压器的损耗。具体规则为按照时段划分法处理过的负荷曲线,分析负载值与临界点划分法得出的临界负载值的大小关系,决定变压器的投切时机。在负荷处于上升状态时,实际运行负荷值如果超过变压器并、分列运行的临界负荷值,此时可以投入备用变压器,并且此段时间内不可以退出。在负荷处于下降状态时,实际运行负荷值如果低于变压器并、分列运行的临界负荷值,此时可以退出备用变压器,并且此段时间内不允许再次投入。在负荷保持不变阶段,需要根据实际负荷的发展趋势做出改变。
4.2. 算例分析
变压器并列运行在理论上来说,只要符合并列运行的条件即可,然而在实际应用中,供电企业一般只允许容量相同的变压器进行并联扩容并且互为备用。对于不同容量的变压器,只允许其一次侧并列,二次侧母线分段,中间设联络开关,即分列运行。因此,根据城市小区的实际情况,算例中选取两台变压器分列运行进行分析。
算例选取的数据是通过短期预测得到的一个周期的整点负荷数据,如表1所示。由于每天负荷是实时变化的,故将负荷数据用每小时的平均负荷表示,共24个整点负荷数据,这样不仅方便数据处理,而且基本不会影响结果的有效性与准确性。
本文以两台常用型号的配电变压器作为例,验证改进的变压器经济运行分析方法。分别将两台变压器编号为变压器A与变压器B。两台变压器的参数如表2所示。
根据以上两台变压器的参数,利用临界点划分法中的分列运行公式求得两台变压器三种不同运行方式的临界负载
通过计算得到两台变压器分列运行的临界负荷值之后,根据临界点划分法结合24个整点负荷数据,可以得到不同时段的变压器运行方式,如表3所示。
按照表1整点负荷预测结果,根据全天24点的负荷值画出负荷预测曲线,如图5所示。
根据本文时段划分法的规则,对负荷预测曲线进行处理,处理结果依次为图6、图7和图8。
Table 1. Hourly load data
表1. 整点时刻负荷数据
Table 2. Transformer parameters
表2. 变压器参数
Table 3. The critical point division method is obtained by the transformer operation mode
表3. 临界点划分法得到的变压器运行方式
Table 4. Improved method of transformer operation
表4. 改进法得到的变压器运行方式

Figure 5. Calculation of load forecasting curve
图5. 算例负荷预测曲线
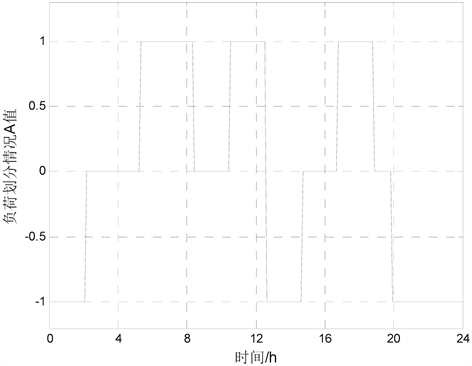
Figure 6. Preliminary results of case study load division
图6. 算例负荷划分初步结果
结合临界点划分法得到的临界负荷值和通过时段划分法得到的负荷变化结果,可以得到改进的变压器经济运行的划分区间,如表4所示。
通过对比临界点划分法和改进的投切策略的投切次数,如表5所示,可以看出改进的投切策略在投切次数上比临界点划分法少4次,有效的减少了变压器的投切次数。
在投切次数上改进的投切策略具有明显优势,在减少损耗方面比较如表6所示,可以看出损耗也降低很多。
由表6可以看出,不采取优化运行时,变压器A与变压器B一周内有功功率损耗为795.75 kWh,而

Figure 7. Calculate the load division again
图7. 算例负荷划分再次结果

Figure 8. Calculate the final result of the load
图8. 算例负荷最终划分结果
Table 5. Comparison of switching times in different ways
表5. 不同方式下投切次数比较
Table 6. Comparison of before and after optimization
表6. 优化前后的损耗比较
经过本文算法优化的投切策略可以把有功功率损耗降低至386.72 kWh。按照此方法,一年按48周计算,总共可以节省电量约18562.56 kWh,按照市电单价为0.5元/kWh计算,每年可以节省经济效益9281.28元。
5. 结论
本文先对时段划分法进行了介绍,进而引出改进的变压器经济运行投切策略,并对其进行了深入理论分析。通过算例分析,改进的变压器经济运行投切策略可以有效的降低变压器损耗和投切次数。
文章引用
张 靓,张茂群,陈登明,章 昊,王建元,史海涛. 改进的变压器组优化运行控制策略
Improved Control Strategy of Optimization Operation of Transformer Bank[J]. 电力与能源进展, 2018, 06(01): 74-83. http://dx.doi.org/10.12677/AEPE.2018.61008
参考文献 (References)
- 1. 董志恒, 胡国元. 电力变压器经济运行[J]. 电气制造, 2012(11): 32-36.
- 2. 秦伟峰. 基于变压器经济运行的10 kV配电网节能降损研究[J]. 中国高新技术企业, 2013(28): 84-85.
- 3. 马晓通. 郑州大学配电网变压器经济运行及综合测控系统研究[D]: [硕士学位论文]. 郑州: 郑州大学, 2012.
- 4. 许迪. 综合考虑网损及投资运行费用的变压器经济运行区间探讨[J]. 电气开关, 2012, 4(3): 10-13.
- 5. 常炳双, 辛健. 配电变压器经济运行模式的探讨[J]. 电网技术, 2007, 31(1): 247-248.
- 6. 卢志刚, 李爽, 韩彦玲, 等. 配电网技术经济运行区域的研究及应用[J]. 高电压技术, 2007, 33(6): 156-159.
- 7. 潘丹涛. 配电变压器的经济运行[J]. 东北电力技术, 2011, 2(3): 30-32.
- 8. 余楚云. 配电系统变压器经济运行方式及其最优投切策略研究工[D]: [硕士学位论文]. 上海: 上海交通大学, 2009.
- 9. 周和平, 张艳秋. 现行电价政策与变压器经济运行[J]. 电气时代, 2011(3): 68-70.
- 10. 张旭明, 张焰, 汪宇霆, 等. 采用禁忌搜索算法的多时段变压器经济运行方式优化[J]. 电网技术, 2010, 34(7): 109-113.
- 11. 张泓泽, 王宝, 郭森. 计及负荷增长的台区配电变压器容量最优选择[J]. 电工技术, 2012(4): 22-24.
- 12. Samet, H., Ghanbari, T. and Ghaisari, J. (2015) Maximum Performance of Electric Arc Furnace by Optimal Setting of the Series Reactor and Transformer Taps Using a Nonlinear Model. IEEE Transactions on Power Delivery, 30, 764-772.
https://doi.org/10.1109/TPWRD.2014.2336693
