设为首页 加入收藏 期刊导航 网站地图

Geomatics Science and Technology
Vol.05 No.03(2017), Article ID:21356,6 pages
10.12677/GST.2017.53018

Accuracy Analysis of Single Point Positioning Using Doppler Smoothed Pseudorange Observations

Yonglin Zhang, Changsheng Cai, Qingfeng Sun, Zhounan Dong

School of Geosciences and Information Physics, Central South University, Changsha Hunan

Received: Jun. 25th, 2017; accepted: Jul. 10th, 2017; published: Jul. 13th, 2017

ABSTRACT

The C/A code observations have large noise and are easily contaminated by multipath errors. By contrast, the Doppler values have good accuracy and are not disturbed by multipath. The Doppler smoothed pseudorange (DSPR) is used to improve the accuracy of pseudorange. Experiments were carried out in the multipath and multipath–free environments. Results show that the DSPR can improve the positioning accuracy. Especially in the multipath environment, the DSPR can improve the accuracy by 26%, 30% and 6% in east, north and up directions, respectively.

Keywords:Doppler, Pseudorange, Multipath, GPS

多普勒观测值平滑伪距单点定位精度分析

张永林，蔡昌盛，孙清峰，董州楠

中南大学地球科学与信息物理学院，湖南 长沙

收稿日期：2017年6月25日；录用日期：2017年7月10日；发布日期：2017年7月13日

摘 要

GPS伪距观测值测量噪声大，易受多路径等误差影响，而多普勒观测值具有较好的观测精度且不受多路径误差的干扰。本文采用多普勒平滑伪距观测值进行单点定位解算。在有多路径误差和无多路径误差下分别进行实验，结果表明多普勒平滑伪距能有效改善单点定位的精度，在多路径环境下，东，北，高三个方向上的改善率分别为26%、30 % 和6%。

关键词 :多普勒，伪距，多路径，GPS

Copyright © 2017 by authors and Hans Publishers Inc.

This work is licensed under the Creative Commons Attribution International License (CC BY).

http://creativecommons.org/licenses/by/4.0/

1. 引言

目前，GPS已广泛应用于导航、工程测绘、地震监测、低轨卫星定轨等多方面 [1] [2] 。但是，GPS伪距观测值测量噪声较大，易受多路径误差干扰，而多普勒观测值具有较好的观测精度且不受多路径误差的干扰。利用多普勒观测值与伪距进行联合单点定位，可以提高定位的精度和稳定性。当前已有学者对多普勒观测值在定位和导航中的应用进行了研究。Chen等人研究了多普勒观测值在GPS和北斗快速定位中的应用 [3] [4] ；Li等研究结果表明使用多普勒联合伪距观测值进行定位的效果优于单独使用伪距观测值 [5] ；Cheng等研究了多普勒平滑伪距的可行性 [6] [7] ；Zair等研究利用多普勒和伪距观测值在多路径误差影响下进行粗差探测 [8] ；此外，还有学者对多普勒测速误差 [9] 、载波平滑伪距联合多普勒观测值的动态滤波 [10] 、遮挡环境下多普勒联合伪距定位等方面进行了研究 [11] 。

以上这些研究工作表明融入多普勒观测值可以有效改善伪距定位的性能。本文首先分析了采样间隔对多普勒平滑伪距效果的影响，然后采用多普勒平滑伪距观测值方法进行单点定位，分别在多路径和无多路径环境下分析了增加多普勒观测值后定位精度的改善情况。

2. 多普勒平滑伪距观测值定位

基本的多普勒平滑伪距公式可以表达如下 [6] ：

(1)

其中表示第i + 1历元的伪距平滑值，表示在第i + 1历元的测码伪距观测值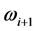；表示i + 1历元的平滑权重因子(SWF)；表示用多普勒计算出的历元间距离变化量，计算公式如下所示：

(2)

上式中，表示载波的波长，表示相邻两历元间的时间间隔，表示第i历元的多普勒观测值。

假设每个历元的多普勒观测值噪声都相等，用表示，利用误差传播公式计算(2)中的方差如下式(3)所示：

(3)

由上式(3)式可以看出，不同于载波平滑伪距，多普勒观测值平滑伪距受到历元间隔的限制，如果历元间隔过大，则无法用多普勒观测值平滑伪距。

3. 数据处理结果与分析

3.1. 无多路径误差下实验

为了验证多普勒平滑伪距算法的有效性，实验采用了IGS参考站KIRU站在2016年第41的数据，观测文件的历元间隔为1 s，观测时段从0点0分到0点15分共900个历元的数据，采用IGS提供的坐标作为参考坐标。

首先分析采样间隔对多普勒平滑伪距效果的影响。对采样间隔分别为1 s，30 s的伪距，多普勒，载波观测值计算历元间站星距离的变化量，以载波计算的变化量为基准，分别与伪距和多普勒的计算值相减，结果如图1，图2所示。从图1可以很容易看到多普勒计算的距离变化量偏差值很小，伪距计算的变化量波动远大于多普勒计算的变化量。从图2可以看到使用多普勒计算的距离变化量偏差值略好于伪距，不合适进行多普勒平滑伪距。需要注意的是，在文献 [7] 中提到使用某些类型的接收机观测到的多普勒频移计算出的距离差与载波计算的距离差之间存在一个稳定的偏差，在使用时必须消除，文献 [12] 中介绍了一种消除偏差的方法，可以参照该方法进行消除。

文献 [7] 中采取的方法是先用双频消电离层组合，然后进行多普勒平滑。考虑到当前应用较广泛的都是单频接收机，本次实验采用的是单频多普勒平滑伪距，采样间隔为1 s，平滑窗口大小为100 [13] 。多普勒平滑伪距定位结果如图3所示。

Figure 1. Epoch-between range variation biases computed by pseudorange and doppler with respect to the one derived from carrier phase at an epoch interval of 1 s

图1. 采样间隔为1 s时用伪距和多普勒计算的历元间距离差分别与载波计算的距离差相减的结果

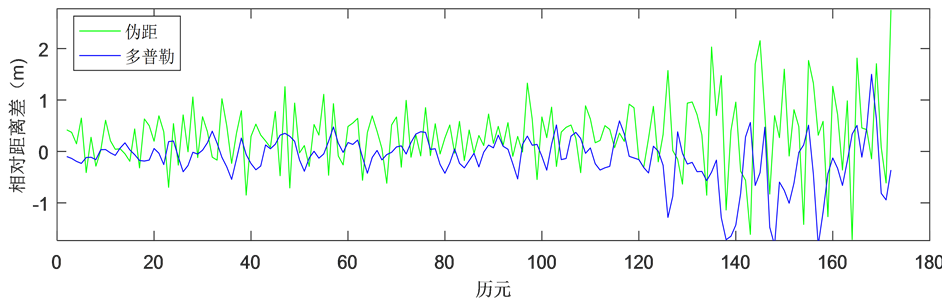
Figure 2. Epoch-between range variation biases computed by pseudorange and doppler with respect to the one derived from carrier phase at an epoch interval of 30 s

图2. 采样间隔为30 s时用伪距和多普勒计算的历元间距离差分别与载波计算的距离差相减的结果

Figure 3. The positioning result of doppler smoothed pseudorange

图3. 多普勒平滑伪距定位结果

从图3可以看到，多普勒平滑伪距解算结果的精度明显高于单独使用伪距解算结果的精度，特别是从第500历元开始，多普勒平滑伪距解算结果更加稳定。表1给出了伪距与多普勒平滑伪距定位结果的均方根误差(RMS)。因为高程方向上参考坐标与实际解算结果的偏差要大于水平方向，故表1中多普勒平滑伪距在水平方向RMS的改善率要高于高程方向。

3.2. 有多路径干扰下实验

在实际观测情况下伪距易受多路径噪声的影响，因此实验模拟对伪距观测值加入多路径误差，如图4所示。下面使用多普勒平滑伪距处理加入多路径误差后的数据，结果如图5所示。

对比表1和表2可知，在多路径噪声的干扰下，伪距定位结果的RMS值在东、北、高程方向上分别增加了约9 cm、15 cm、6 cm；多普勒平滑伪距定位结果的RMS值在东、北、高程方向上分别增加了约6 cm、5 cm、1 cm。多普勒平滑伪距精度下降幅度低于单独使用伪距定位的精度下降幅度。从表中的精度改善百分比来看，多普勒平滑伪距在多路径误差干扰情况下对伪距定位精度的提升率优于无多路径干扰情况下的提升率。由于多普勒观测值不受多路径误差的影响，因而在多路径环境下，使用多普勒平滑伪距可以有效减弱多路径误差对定位结果的影响。

4. 结论与展望

在伪距单点定位中引入多普勒观测值，通过实验验证了多普勒平滑伪距的可行性。实验结果表明，多普勒平滑伪距能较好地改善伪距定位的精度，提高定位解的稳定性。多普勒平滑伪距方法在多路径环境下的改善效果好于无多路径下的改善效果。在多路径环境下，多普勒平滑伪距方法在东、北、高程的精度改善分别为26%、30%、6%。

考虑到伪距观测值和多普勒观测值都会受到粗差的影响，分析多普勒观测值中存在粗差的情况下对平滑伪距定位方法的影响，寻找剔除多普勒观测值中粗差的方法需要进一步展开研究。此外，多普勒观测值可以用来测量接收机的速度，分析多普勒观测值的测速精度，研究在动态情况下多普勒联合伪距的定位方法也是今后进一步研究的方向。

Figure 4. The simulated multipath error

图4. 模拟的多路径误差

Figure 5. Positioning results using doppler smoothed pseudorange with simulated multipath errors

图5. 在多路径干扰下多普勒平滑伪距定位结果

Table 1. The precision analysis of doppler smoothed pseudorange

表1. 伪距与多普勒平滑伪距定位结果RMS统计(m)

Table 2. The precision analysis of positioning solutions using doppler smoothed pseudorange with simulated multipath errors

表2. 多普勒平滑伪距在多路径条件下的定位精度比较(m)

基金项目

国家自然科学基金项目(No.41674039)；中南大学研究生科研创新项目(No.1053320171217)。

文章引用

张永林,蔡昌盛,孙清峰,董州楠. 多普勒观测值平滑伪距单点定位精度分析
Accuracy Analysis of Single Point Positioning Using Doppler Smoothed Pseudorange Observations[J]. 测绘科学技术, 2017, 05(03): 152-157. http://dx.doi.org/10.12677/GST.2017.53018

参考文献 (References)

  1. 1. 张小红, 郭博峰. 单站GPS测速在实时地震监测中的应用[J]. 地球物理学报, 2013, 56(6): 1928-1936.

  2. 2. Yang, Y., Yue, X. and Dempster, A.G. (2015) GPS-Based Onboard Real-Time Orbit Determination for Leo Satellites Using Consider Kalman Filter. IEEE Transactions on Aerospace & Electronics Systems, 52, 769-777. https://doi.org/10.1109/TAES.2015.140758

  3. 3. Chen, H.W., Wang, H.S., Chiang, Y.T. and Chang, F.R. (2014) A New Coarse-Time GPS Positioning Algorithm Using Combined Doppler and Code-Phase Measurements. GPS Solutions, 18, 541-551. https://doi.org/10.1007/s10291-013-0350-8

  4. 4. Jing, S., Xu, B., Yong, L. and Sun, G. (2015) Doppler-Aided Rapid Positioning Method for Bds Receivers. Electronics Letters, 51, 2139-2141. https://doi.org/10.1049/el.2015.1033

  5. 5. Li, L., Zhong, J. and Zhao, M. (2011) Doppler-Aided GNSS Position Estimation with Weighted Least Squares. IEEE Transactions on Vehicular Technology, 60, 3615-3624. https://doi.org/10.1109/TVT.2011.2163738

  6. 6. Cheng, P. (1999) Remarks on Doppler-Aided Smoothing of Code Ranges. Journal of Geodesy, 73, 23-28. https://doi.org/10.1007/s001900050214

  7. 7. Zhou, Z. and Li, B. (2017) Optimal Doppler-Aided Smoothing Strategy for GNSS Navigation. GPS Solutions, 21, 197-210. https://doi.org/10.1007/s10291-015-0512-y

  8. 8. Zair, S., Hégarat-Mascle, S.L. and Seignez, E. (2016) Outlier Detection in GNSS Pseudo-Range/Doppler Measurements for Robust Localization. Sensors, 16, 580. https://doi.org/10.3390/s16040580

  9. 9. 何海波, 杨元喜, 孙中苗, 等. GPS多普勒频移测量速度模型与误差分析[J]. 测绘科学技术学报, 2003, 20(2): 79-82.

  10. 10. 周泽波, 沈云中, 李博峰. 基于相位平滑伪距与多普勒数据的GPS动态定位[J]. 大地测量与地球动力学, 2008, 28(3): 59-63.

  11. 11. Ji, H.F. (2014) The New Doppler Shift-and-Range Positioning Algorithm for the Global Navigation Satellite System. Astronomical Research & Technology, 11, 13-18.

  12. 12. Mouri, A., Kubo, Y. and Sugimoto, S. (2015) Detection and Correction of Doppler Biases in Kalman Filter-Based Positioning. Transactions of the Institute of Systems Control & Information Engineers, 2015, 156-164.

  13. 13. Park, B., Sohn, K. and Kee, C. (2008) Optimal Hatch Filter with An Adaptive Smoothing Window Width. Journal of Navigation, 61, 435-454. https://doi.org/10.1017/S0373463308004694

期刊菜单