Advances in Applied Mathematics
Vol.
11
No.
08
(
2022
), Article ID:
54852
,
10
pages
10.12677/AAM.2022.118604
H-张量的新判定准则及其应用
赵鹏程
贵州民族大学数据科学与信息工程学院,贵州 贵阳
收稿日期:2022年7月15日;录用日期:2022年8月9日;发布日期:2022年8月17日

摘要
H-张量在科学与工程实践等领域中有着重要的应用,但在实际中要判定H-张量是比较困难的。本文通过构造不同的正对角阵,结合不等式的放缩技巧,给出了H-张量比较实用的新判别条件。作为应用,给出了判定偶次齐次多项式正定性的新方法,并给出相应的数值算例,表明了新结论的有效性。
关键词
H-张量,齐次多项式,正定性,不可约,非零元素链

New Criterions for H-Tensors and Its Applications
Pengcheng Zhao
College of Data Science and Information Engineering, Guizhou Minzu University, Guiyang Guizhou
Received: Jul. 15th, 2022; accepted: Aug. 9th, 2022; published: Aug. 17th, 2022

ABSTRACT
H-tensors have important applications in science and engineering, but it is difficult to determine whether a given tensor is an H-tensor or not in practice. In this paper, by constructing different positive diagonal matrices and combining the technique of inequality reduction, new practical conditions for H-tensors are given. As applications, new methods for determining the positive definiteness of even homogeneous polynomials are presented, and the validity of new results is verified by some numerical examples.
Keywords:H-Tensors, Homogeneous Multivariate Forms, Positive Definiteness, Irreducible, Nonzero Elements Chain

Copyright © 2022 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
张量是高阶广义矩阵,广泛应用于信号和图像处理、高阶统计学、自动控制、医学成像、超图理论、弹性材料科学和工程研究与数据分析等领域中。近年来,许多专家学者对一般张量 [1] - [6] 或特殊结构张量的理论、性质及应用进行了广泛探讨 [7] - [18]。本文继续讨论H-张量的判定问题,得到了只与张量元素有关的新判别不等式,拓广了文献 [11] [14] [15] [16] 的结果。同时,获得了偶数阶实对称张量,即偶数阶齐次多项式正定性的新判定条件。最后,利用数值算例说明了新条件的有效性。
2. 预备知识
记
为复(实)数集,
。一个m阶n维张量
由
个元素构成,其中
,, [3] [4]。若
,,则称
为对称张量 [5],其中
为m个指标的置换群。称张量
为单位张量 [5],若
若
,,,
则称m阶n次齐次多项式
是正定的 [3]。
也可以表示为m阶n维对称张量
与
的乘积,如下
.
若
是正定的,则对称张量
也是正定的 [3]。
定义1 [8] 设
是m阶n维张量,若存在正向量
,满足
,,
则称
为H-张量。
定义2 [5] 设
是m阶n维张量,若存在一个非空子集
,满足
,,,
则称
是可约张量。否则,称
是不可约张量。
定义3 [9] 设
是m阶n维张量,若存在指标
,满足
,,,
其中
,,则称张量
中有一条从指标i到指标j的非零元素链。
3. 主要结果
为讨论方便,给出如下记号:设
是m阶n维张量,令
,
,
,
,,
,,
,,
,
.
引理1 [6] 若
是严格对角占优的张量,则
是H-张量。
引理2 [10] 设
是m阶n维张量。若存在正对角阵
,满足
是H-张量,则
是H-张量。
引理3 [6] 设
是m阶n维张量且不可约。若
,,
且上式中至少有一个严格不等式成立,则
是H-张量。
引理4 [9] 设
是m阶n维张量。若
1)
, ;
2)
;
3)
,从指标i到指标j有一条非零元素链,满足
;
则
是H-张量。
定理1 设
是m阶n维张量。若
满足
,, (1)
且
(
),则
是H-张量。
证明:由K的定义知
.
因此
,. (2)
由式(1)得,
. (3)
而
且
,所以
,. (4)
由(3)式和(4)式得,一定存在足够小的正数
,使得
,, (5)
,. (6)
构造正对角阵
,记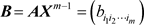 ,其中
,其中
, ;
, ;
,.
而
且
,故对
,
根据(6)式,对
,
对
,由(2)式得
综上可得
。由引理1知
是H-张量,故由引理2知
是H-张量。
定理2 设
是m阶n维张量且不可约。若
满足
,, (7)
且(7)式中至少有一个严格不等式成立,则
是H-张量。
证明:构造正对角阵
,记
,其中
, ;
, ;
,.
由M的定义得,对
,
根据(7)式知,对
,
又对
,由K的定义知
因此,
。因(7)式中至少有一个严格不等式成立,所以存在指标
满足
,且由
不可约知
不可约,于是由引理3知
是H-张量。从而,由引理2知
是H-张量。
记
定理3 设
是m阶n维张量。若
满足
,, (8)
且对
, 中存在从i到j的非零元素链,满足
,则
为H-张量。
证明:构造正对角阵
,记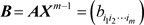 ,其中
,其中
, ;
, ;
,.
类似于定理2的证明,对任意的
,有
,且至少有一个严格不等式成立。
另一方面,若
,则
。设
中有从i到j的一条非零元素链,满足
,则
中也有从i到j一条非零元素链,满足
。于是,由引理4知
是H-张量,再由引理2知
是H-张量。
例1 设 是一个3阶3维张量,其中
是一个3阶3维张量,其中
,,.
则
,,,,,.
所以
。计算得
,,,,.
因为
,
所以张量
满足本文定理1的条件,故张量
为H-张量。但
,
且
因此
不满足文献 [11] 中定理1的条件且
不满足文献 [14] 中定理2的条件。
4. 应用
基于H-张量的新判定条件,下面给出判定高次多元偶次齐次多项式正定性的新结论。
引理5 [6] 设
是m阶n维的实对称张量,m是偶数,
。若
是H-张量,则
是正定的。
根据引理5,定理1,定理2和定理3,可得到以下结论。
定理4设m阶n维张量
为偶数阶实对称张量,
。若
满足下列条件之一:定理1的条件;或定理2的条件;或定理3的条件,则
是正定的。
例2 设6次齐次多项式
其中
是一个6阶6维实对称张量,且
其余的
。则
,,,,,,
且
。计算得
,,,,.
当
时,计算得
因此
满足本文定理1的条件,由定理4知
是正定的,即
是正定的。但
,
,
且
,
因此不能用 [15] 中的定理3, [16] 中的定理4和 [11] 中的定理1判断
的正定性。
5. 结论
本文通过构建不同的正对角矩阵,结合不等式的放缩技巧,得到了判别H-张量的新不等式,且这些不等式只涉及到张量的元素关系,因此它们是容易计算的。作为应用,给出了偶数阶实对称张量,即高次多元偶次齐次多项式正定性的判定新方法,数值例子表明了新结论的有效性。下一步,H-张量的高效数值迭代判定算法将是研究的重点。
致谢
感谢编辑老师和审稿老师提出了宝贵修改意见。
基金项目
贵州省科学技术基金(20181079,20191161),贵州民族大学自然科学基金(GZMU[2019]YB08)。
文章引用
赵鹏程. H-张量的新判定准则及其应用
New Criterions for H-Tensors and Its Applications[J]. 应用数学进展, 2022, 11(08): 5727-5736. https://doi.org/10.12677/AAM.2022.118604
参考文献
- 1. Chang, K.C., Pearson, K. and Zhang, T. (2008) Perron-Frobenius Theorem for Nonnegative Tensors. Communications in Mathematical Sciences, 6, 507-520. https://doi.org/10.4310/CMS.2008.v6.n2.a12
- 2. Liu, Y.J., Zhou, G.L. and Ibrahim, N.F. (2010) An Always Convergent Algorithm for the Largest Eigenvalue of an Irreducible Nonnegative Tensor. Journal of Computational and Applied Mathematics, 235, 286-292.
https://doi.org/10.1016/j.cam.2010.06.002
- 3. Qi, L. (2005) Eigenvalues of a Real Supersymetric Tensor. Journal of Symbolic Computation, 40, 1302-1324.
https://doi.org/10.1016/j.jsc.2005.05.007
- 4. Lim, L.H. (2005) Singular Values and Eigenvalues of Tensors: A Variational Approach. Proceedings of the IEEE International Workshop on Computational Advances in Multi-Sensor Adaptive Processing, Puerto Vallarta, Vol. 1, 129-132.
- 5. Yang, Y.N. and Yang, Q.Z. (2011) Further Results for Perron-Frobenius Theorem for Nonnegative Tensors II. SIAM Journal on Matrix Analysis and Applications, 32, 1236-1250. https://doi.org/10.1137/100813671
- 6. Li, C.Q., Wang, F., Zhao, J.X., et al. (2014) Criterions for the Positive Definiteness of Real Supersymmetric Tensors. Journal of Computational and Applied Mathematics, 255, 1-14. https://doi.org/10.1016/j.cam.2013.04.022
- 7. Kannana, M.R., Mondererb, N.S. and Bermana, A. (2015) Some Properties of Strong H-Tensors and General H-Tensors. Linear Algebra and Its Applications, 476, 42-55. https://doi.org/10.1016/j.laa.2015.02.034
- 8. Ding, W., Qi, L. and Wei, Y. (2013) M-Tensors and Nonsingular M-Tensors. Linear Algebra and Its Applications, 439, 3264-3278. https://doi.org/10.1016/j.laa.2013.08.038
- 9. Wang, F. and Sun, D.S. (2016) New Criteria for H-Tensors and an Application. Journal of Inequalities and Applications, 96, 1-12. https://doi.org/10.1186/s13660-016-1041-0
- 10. Wang, F., Sun, D.S., Zhao, J.X., et al. (2017) New Practical Cri-teria for H-Tensors and Its Application. Linear and Multilinear Algebra, 65, 269-283. https://doi.org/10.1080/03081087.2016.1183558
- 11. Li, Y.T., Liu, Q.L. and Qi, L. (2017) Programmable Criteria for Strong H-Tensors. Numerical Algorithms, 74, 199-221.
https://doi.org/10.1007/s11075-016-0145-4
- 12. Zhang, L.P., Qi, L. and Zhou, G.L. (2014) M-Tensors and Some Applications. SIAM Journal on Matrix Analysis and Applications, 35, 437-542. https://doi.org/10.1137/130915339
- 13. Zhang, K.L. and Wang, Y.J. (2016) An H-Tensor Based Iterative Scheme for Identifying the Positive Definiteness of Multivariate Homogeneous Forms. Journal of Computational and Applied Mathematics, 305, 1-10.
https://doi.org/10.1016/j.cam.2016.03.025
- 14. Bai, D.J. and Wang, F. (2021) New Methods Based H-Tensors for Identifying the Positive Definiteness of Multivariate Homogeneous Forms. AIMS Mathematics, 6, 10281-10295. https://doi.org/10.3934/math.2021595
- 15. Qi, L. and Song, Y.S. (2014) An Even Order Symmetric B-Tensor Is Positive Definite. Linear Algebra and Its Applications, 457, 303-312. https://doi.org/10.1016/j.laa.2014.05.026
- 16. Li, C.Q. and Li, Y.T. (2015) Double B-Tensors and Quasi-Double B-Tensors. Linear Algebra and Its Applications, 466, 343-356. https://doi.org/10.1016/j.laa.2014.10.027
- 17. Bai, D.J. and Wang, F. (2022) New Criterions-Based H-Tensors for Testing the Positive Definiteness of Multivariate Homo-geneous Forms. Mathematics, 10, Article No. 2416. https://doi.org/10.3390/math10142416
- 18. Lv, C.Q. and Ma, C.F. (2021) An Iterative Scheme for Identifying the Positive Semi-Definiteness of Even-Order Real Symmetric H-Tensor. Journal of Computational and Applied Mathematics, 392, Article ID: 113498.
https://doi.org/10.1016/j.cam.2021.113498






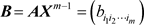 ,其中
,其中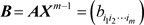 ,其中
,其中 是一个3阶3维张量,其中
是一个3阶3维张量,其中