 Journal of Water Resources Research 水资源研究, 2012, 1, 175-185 http://dx.doi.org/10.12677/jwrr.2012.14025 Published Online August 2012 (http://www.hanspub.org/journal/jwrr.html) Impact of Potential Evapotranspiration on Runoff Simulation in Hanjiang Basin* Lihua Xiong, Xiaolin Zhang, Lin Lin, Shuai Li State Key Laboratory of Water Resources and Hydropower Engineering Science, Wuhan University, Wuhan Email: 698zhangxiaolin@163.com Received: Mar. 16th, 2012; revised: Mar. 28th, 2012; accepted: Apr. 11th, 2012 Abstract: The FAO-56 Penman-Monteith equation (PM) and four other temperature-based equations, i.e. Hargreaves (Har), Blaney-Criddle (B-C), Thornthwaite (Tho) and Hamon (Ham), were used to estimate the monthly potential evapotranspiration at 41 sub catchments in Hanjiang basin. The monthly runoff of each catchment was then simulated using the two-parameter monthly water balance model based on the estimated potential evapotranspiration data. The parameter calibration method was chosen to be SCE-UA algorithm. A comparison among the simulation results using five different monthly potential evapotranspiration equations showed that: 1) The average model efficiency of two-parameter monthly water balance model over 41 sub catchments is more than 80% for each different monthly potential evapotranspiration equation; 2) The simula- tion result is best when using the Ham equation, with the model efficiency at each of 41 catchment larger than 70%, while the result s of t he P M , Har, and B-C equations are relatively poo r, and the Tho met hod i s t he worst. Keywords: Potential Evapotranspiration; Monthly Water Balance Model; Runoff Simulation; Hanjiang Basin 潜在蒸散发公式对汉江流域径流模拟结果的影响* 熊立华,张晓琳,林 琳,李 帅 武汉大学水资源与水电工程科学国家重点实验室,武汉 Email: 698zhangxiaolin@163.com 收稿日期:2012 年3月16 日;修回日期:2012 年3月28 日;录用日期:2012 年4月11 日 摘 要:采用 FAO-56 Penman-Monteith (PM)、Hargreaves (Har)、Blaney-Criddle (B-C)、Thornthwaite (Tho) 和Hamon (Ham)等5种潜在蒸散发公式计算汉江 41 个子流域的月潜在蒸散发量,将其作为蒸发输入 数据代入两参数月水量平衡模型中模拟各子流域的月径流过程。模型参数的率定选用 SCE-UA 算法。 径流模拟结果显示:1) 对于每一个潜在蒸散发计算公式,两参数月水量平衡模型在 41 个子流域上的 效率系数的平均值均达到 80%以上;2) 使用 Ham 方法模拟精度最优,每个子流域的效率系数均达到 70%以上,PM 法、Har 和B-C 法略差,Tho 方法模拟精度最差。 关键词:潜在蒸散发;月水量平衡模型;径流模拟;汉江流域 1. 引言 全球变暖是各国政府和科学界共同关心的重大 问题,气候变暖能够加速区域水文循环,使得不同地 区的水资源供需矛盾更加尖锐,因此水资源是受气候 变化影响最直接、最重要的领域。利用流域水文模型 耦合区域气候模式是评价气候变化对水资源影响的 基本途径,为满足生态学研究、干旱分析、气候变化 *基金项目:国家自然科学基金重大项目(51190094)和国家自然科学 基金面上项目(51079098)资助。 作者简介:熊立华(1972-),男,武汉大学教授,博导,主要从事水 文水资源研究。 Copyright © 2012 Hanspub 175  熊立华,等:潜在蒸散发公式对汉江流域径流模拟结果的影响 第1卷 · 第4期 和人类活动影响评价等不同目的,水文工作者根据不 同流域的水文气候特点,相继提出或改进了结构及计 算时段各异的水量平衡模型用于流域水资源和气候 研究。 最早的水量平衡模型可以追溯到 1940 年代, Thornthwaite 和Mather 提出的水量平衡模型在径流模 拟方面非常有效[1]。随后水文学家们发展了很多其他 的水量平衡模型:例如 Palmer 的双土壤层模型[2], Thomas 提出的四参数 abcd 水量平衡模型[3],郭生练 等提出的五参数月水量平衡模型[4],以及熊立华和郭 生练提出的两参数月水量平衡模型[5]等,均取得了良 好的模拟效果。近几十年来,研究者先后对其中的一 些水量平衡模型做了比较分析,获得了相当丰富的经 验[6-8],李帅等人比较了 8种水量平衡模型在中国湿润 地区的模拟效果,结果显示其中 6种水量平衡模型的 模拟效果良好[9]。本文选用熊立华和郭生练提出的两 参数月水量平衡模型模拟汉江流域的月径流过程,比 较5种不同潜在蒸散发计算公式对汉江 41 个子流域 月径流模拟的影响。 2. 5种潜在蒸散发计算公式 常用的估算潜在蒸散发量的方法有很多种,如水 汽输送法、热量平衡法、彭曼法和经验公式法等[10]。 近些年,国内外开展了大量的对比研究[10,11],结果表 明不同潜在蒸散发公式在不同地区的适用性存在差 异。张晓琳等曾采用PM 公式以及以温度为基础的 B-C、Har、Tho 和Ham 公式 5种计算方法分析汉江 流域的潜在蒸散发量[12]。本文在此基础上,将潜在蒸 散发计算结果应用于两参数月水量平衡模型中,模拟 汉江 41 个子流域的月径流过程。 PM 公式属于综合法,是目前公认的应用最普遍、 精度最高的公式之一[13],缺点是需要详细的气象资 料;其他 4种潜在蒸散发公式均属于温度法,对资料 的要求低,应用灵活方便,在世界各地都得到广泛的 推广和应用[14,15]。5种潜在蒸散发公式的具体计算表 达式见表 1,公式中各参数具体含义及取值可参照文 献[16-18]。 3. 两参数月水量平衡模型及参数率定 3.1. 两参数月水量平衡模型 两参数月水量平衡模型由熊立华和郭生练提出, 概念明确,模拟精度高,在东江、赣江和汉江 70 个 子流域上取得了很好的应用效果[5]。该模型以水量平 衡为理论基础,将各个水文过程或变量之间的关系概 化成经验函数或表达式来模拟流域水文过程,相对于 日尺度模型来说,概化了存在于较短时间尺度上的一 些随机不确定因素,因此模型结构简单,参数少,便 于广泛推广。 两参数模型主要输入数据为月降水量和月蒸发 量,输出数据为实际蒸散发,径流深等。本文降雨量 采用各子流域控制面积内降雨观测值的算术平均值, 径流资料采用各子流域控制站的实测值。已有的研究 成果一般利用蒸发皿蒸发计算实际蒸散发,而潜在蒸 散发同蒸发皿蒸发一样,都是计算实际蒸散发的参数 [19],因此本文采用 5种复杂程度各异的潜在蒸散发计 算公式计算汉江 41 个子流域月潜在蒸散发量,将其作 蒸发输入数据代入两参数月水量平衡模型中,计算 为 Table 1. Potential evaptranspiration equations 表1. 潜在蒸散发计算公式表 名称 潜在蒸散发量 ET0计算公式 经验系数 k PM 2 0 2 900 0.408 273 10.34 ns RG Uee T ET U a Har 12 017.8 Aa ETkR TDT 0.0023 B-C 00.46 8.13 a ET kpT 0.85 Ham ET0 = k × N × Pt 17.27 273.3 0.6108 216.7 273.3 a a T T a e Pt T 0.84 Tho 010 360 a ETkT IuN 0.016 0.5aI 12 1 j Ii 1.5 0.09 jj iT 16 Copyright © 2012 Hanspub 176  熊立华,等:潜在蒸散发公式对汉江流域径流模拟结果的影响 第1卷 · 第4期 实际蒸散发并对汉江 41 个子流域进行月径流模拟。 实际月蒸发量E的计算公式可以写成: 00 tanhEtcETtPtET t (1) Et为第 t个月的实际蒸发量,本文的 0 ETt 为第 t 个月潜在蒸散发量,为第 t个月观测的降水量,c 为模型的第一个参数,通过率定得到。 Pt 月径流量的计算公式为: 1tanh 1Qt StSt SC (2) SC 为流域平均蓄水容量,是模型的第二个参数, St 为第 t个月土壤层净含水量,可由以下公式推算: 1StStPt EtQt (3) 当时, 才用(2)式计算,当 0St Qt 0St 时, 取0,表明土壤里没有任何净含水量,不产生径 流。 Qt 3.2. 参数率定 由于两参数月水量平衡模型概化成两个参数,所 以参数 c和SC必然与流域气候条件和下垫面的特征 有关[20],参数的优选十分必要,在一定程度上决定了 模型的拟合精度。本文为保证模拟结果的有效性和无 偏性,选择 Nash 效率系数 、模拟径流和实测径流 的多年平均相对误差 RE 作为目标函数来衡量模型的 模拟精度。 2 R 1) ,模型效率系数,Nash与Sutcliffe 在1970 年提出[21],计算公式为: 2 R 2 ,, 21 2 , 1 1 n obs isim i in obs iobs i QQ R QQ (4) 这里的 , ,obs i Qobs Q,, s im i Q分别指实测月径流深,实 测月径流深的平均值,模拟的月径流深。 2) RE,模拟径流深和实测径流深的多年平均相对 误差: ,, , n obs isim i in bos i i QQ RE Q (5) 模型效率主要取决于值,越接近于 1,表 明模型效率越高,同时 RE越接近于 0,说明模拟效 2 R2 R 果越好。在率定过程中,一般很难使两者同时达到最 优,需要综合考虑实际需要,率定出满足要求的参数。 参数的自动率定包含两个步骤:第一步,根据目 标函数 RE 初步确定 c和SC;第二步,c值固定为第 一步的率定结果,根据目标函数 二次率定参数 SC。 自动率定模型参数模块用 C++编程,参数率定采用 SCE-UA 算法,SCE-UA 算法是一种全局优化算法, 能够有效快速的搜索到水文模型参数的全局最优解 [22,23],是目前水文模型参数优选中最有效的方法。 2 R 4. 流域简介 汉江是长江中下游最大的支流,发源于秦岭南 麓,干流经陕西、湖北两省,于武汉市汇入长江,全 长1570 余km。流域集水面积 15.9 万km2,地势西北 高,东南低。 汉江流域位于我国南北地理和气候分区的交界区 域,属亚热带季风区,四季温暖,干湿分明,流域多 年平均气温 14℃,年平均相对湿度74%,年平均蒸发 量848 mm,年平均降水量 928 mm,水量丰沛,但年 内分配不均,年际变化较大,洪水多发生在 7~10月, 暴雨强度大,历时短,在未来气候变化的情势下,水 文对其的响应将直接影响到生态环境及其产业结构。 本文选择汉江流域的 41 个子流域作为研究对象,比较 5种不同潜在蒸散发计算公式情形下两参数月水量平 衡模型径流模拟的精度。41 个子流域基本信息见表 2。 5. 应用与结论 将5种潜在蒸散发公式的计算结果分别代入两参 数月水量平衡模型中,对汉江流域41个子流域逐一 进行计算,得到最终的月径流模拟结果。 5.1. 参数率定结果分析 图1和图 2分别为参数 c和SC的空间分布图。 从图中可以看出:模型参数具有一定的地区分布规 律,反映了不同地区自然地理条件与降水径流之间的 关系。 参数 c介于 0.30~1.25 之间,是潜在蒸散发与实际 蒸散发之间的转化系数,反应了不同流域不同潜在蒸 散发公式计算结果与该流域实际蒸散发之间的关系。 Copyright © 2012 Hanspub 177 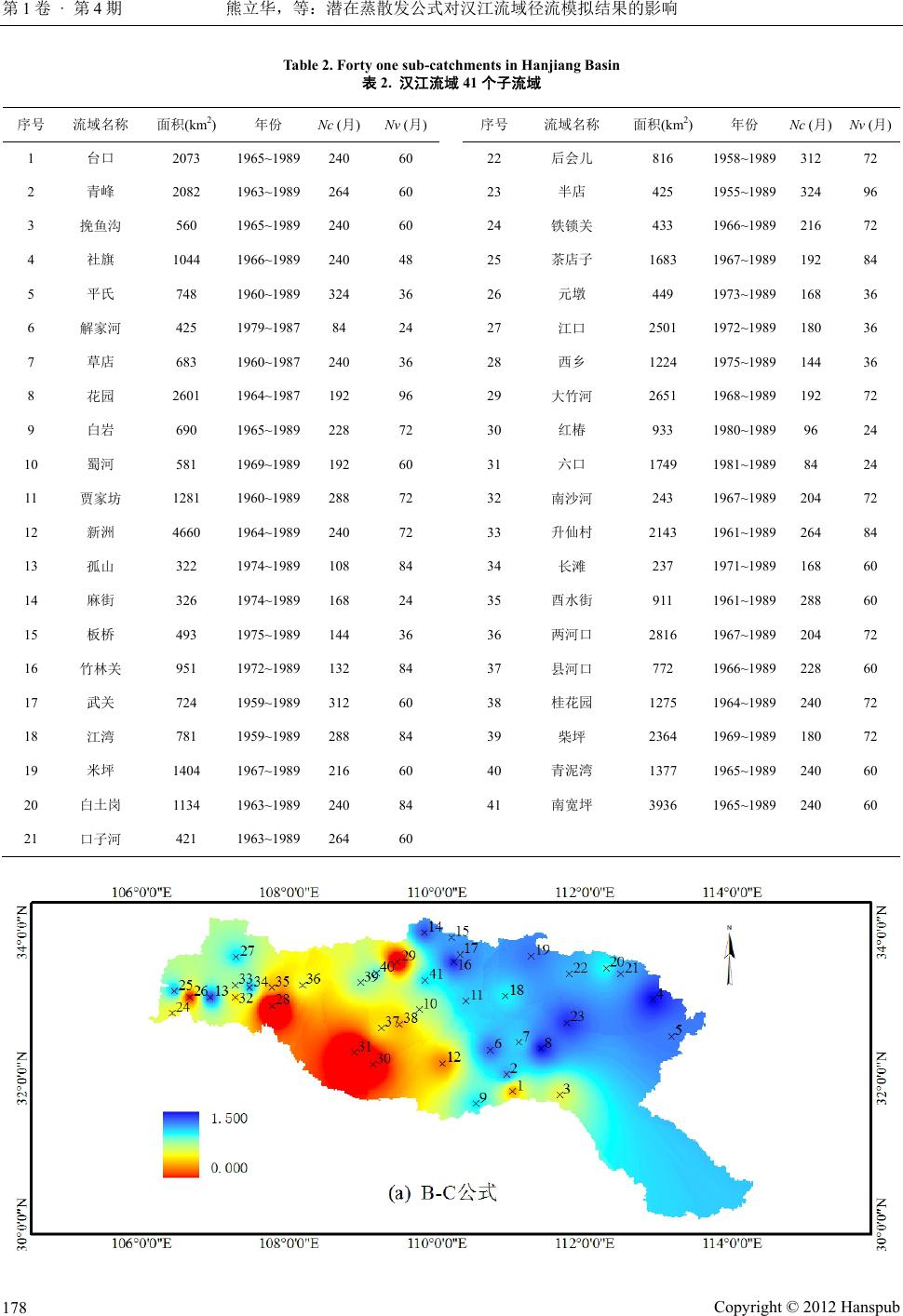 熊立华,等:潜在蒸散发公式对汉江流域径流模拟结果的影响 第1卷 · 第4期 Table 2. Forty one sub-catchments in Hanjiang Basin 表2. 汉江流域 41 个子流域 序号 流域名称 面积(km2) 年份 Nc (月)Nv (月)序号 流域名称 面积(km2) 年份 Nc (月)Nv (月) 1 台口 2073 1965~1989 240 60 22 后会儿 816 1958~1989 312 72 2 青峰 2082 1963~1989 264 60 23 半店 425 1955~1989 324 96 3 挽鱼沟 560 1965~1989 240 60 24 铁锁关 433 1966~1989 216 72 4 社旗 1044 1966~1989 240 48 25 茶店子 1683 1967~1989 192 84 5 平氏 748 1960~1989 324 36 26 元墩 449 1973~1989 168 36 6 解家河 425 1979~1987 84 24 27 江口 2501 1972~1989 180 36 7 草店 683 1960~1987 240 36 28 西乡 1224 1975~1989 144 36 8 花园 2601 1964~1987 192 96 29 大竹河 2651 1968~1989 192 72 9 白岩 690 1965~1989 228 72 30 红椿 933 1980~1989 96 24 10 蜀河 581 1969~1989 192 60 31 六口 1749 1981~1989 84 24 11 贾家坊 1281 1960~1989 288 72 32 南沙河 243 1967~1989 204 72 12 新洲 4660 1964~1989 240 72 33 升仙村 2143 1961~1989 264 84 13 孤山 322 1974~1989 108 84 34 长滩 237 1971~1989 168 60 14 麻街 326 1974~1989 168 24 35 酉水街 911 1961~1989 288 60 15 板桥 493 1975~1989 144 36 36 两河口 2816 1967~1989 204 72 16 竹林关 951 1972~1989 132 84 37 县河口 772 1966~1989 228 60 17 武关 724 1959~1989 312 60 38 桂花园 1275 1964~1989 240 72 18 江湾 781 1959~1989 288 84 39 柴坪 2364 1969~1989 180 72 19 米坪 1404 1967~1989 216 60 40 青泥湾 1377 1965~1989 240 60 20 白土岗 1134 1963~1989 240 84 41 南宽坪 3936 1965~1989 240 60 21 口子河 421 1963~1989 264 60 Copyright © 2012 Hanspub 178 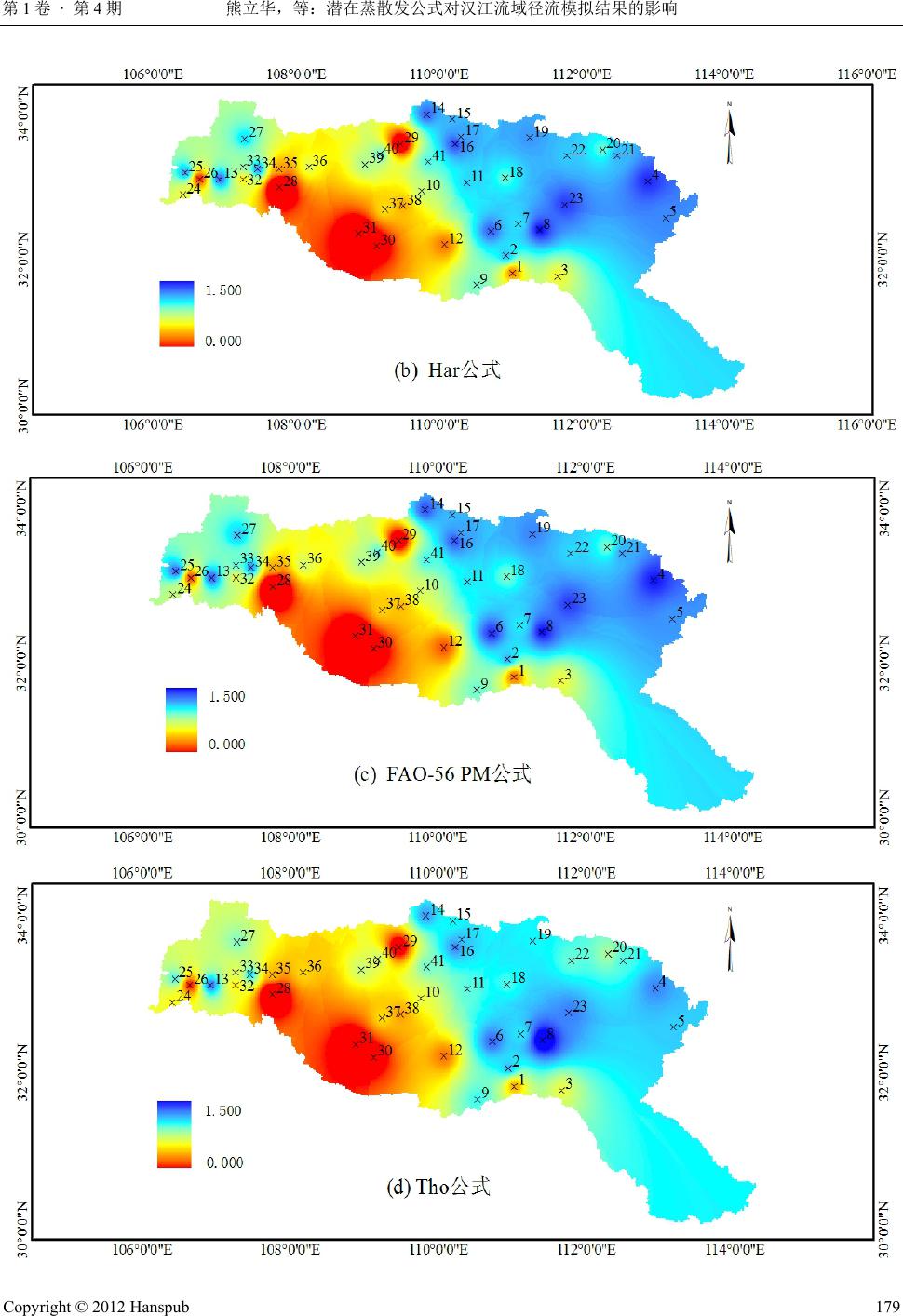 熊立华,等:潜在蒸散发公式对汉江流域径流模拟结果的影响 第1卷 · 第4期 Copyright © 2012 Hanspub 179 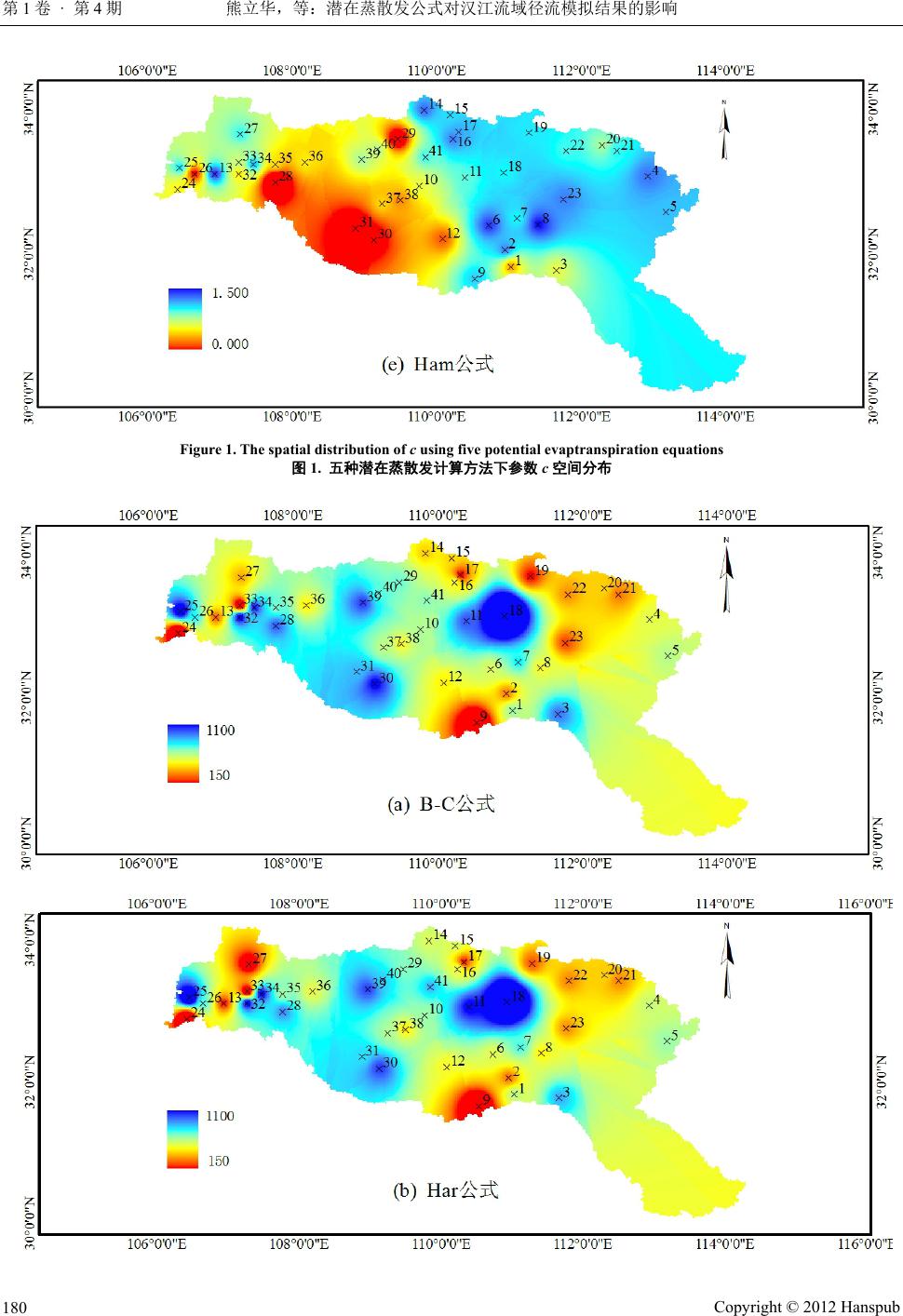 熊立华,等:潜在蒸散发公式对汉江流域径流模拟结果的影响 第1卷 · 第4期 Figure 1. The spatial distribution of c using five potential evaptranspiration equations 图1. 五种潜在蒸散发计算方法下参数 c空间分布 Copyright © 2012 Hanspub 180 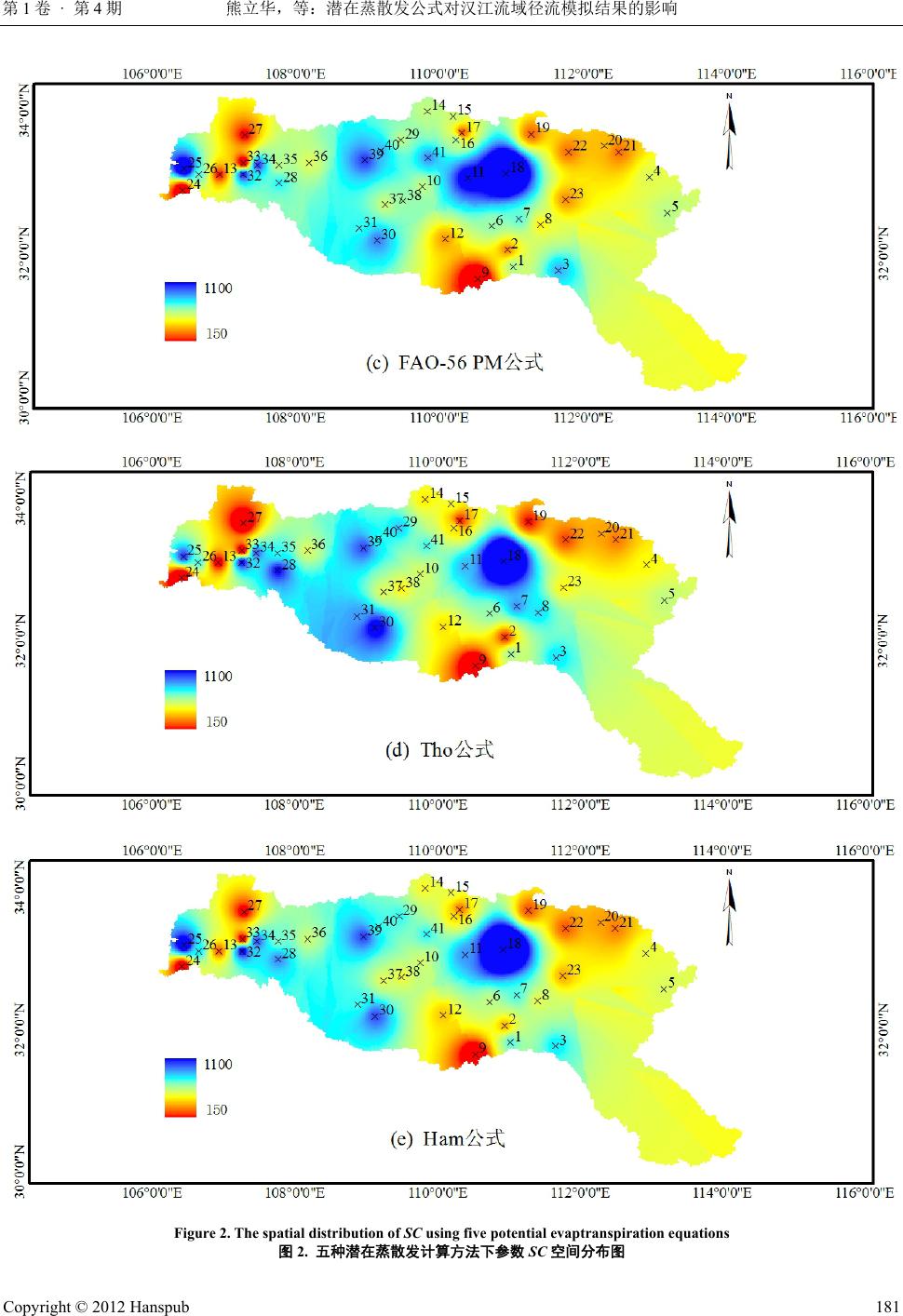 熊立华,等:潜在蒸散发公式对汉江流域径流模拟结果的影响 第1卷 · 第4期 Figure 2. The spatial distribution of SC using five potential evaptranspiration equations 图2. 五种潜在蒸散发计算方法下参数 SC空间分布图 Copyright © 2012 Hanspub 181  熊立华,等:潜在蒸散发公式对汉江流域径流模拟结果的影响 Copyright © 2012 Hanspub 第1卷 · 第4期 182 汉江上游参数c取值较小,中游取值最大,下游取值 居中。参数 SC 介于 150 mm~1100 mm之间,表示流 域最大蓄水能力,反映了不同地区自然地理条件与流 域土壤含水量之间的关系。整体上看,使用Tho 计算 公式时,流域平均蓄水容量SC 最小;使用 PM 计算 公式,流域平均蓄水容量SC 最大。空间分布上,流 域上游土壤含水量较大,江湾流域达到最大值,约 1000 mm;中下游土壤含水量较低。整体分布西北高 东南低,但是也有部分小流域出现了特殊情况,例如 上游的铁锁关、元墩、升仙村、江口附近,流域土壤 含水量略低;下游的挽鱼沟土壤含水量略高。 好的模拟效果。无论是检验期还是率定期,对每一个 潜在蒸散发计算公式,41 个子流域的 的平均值都 在80%以上,RE 绝对值的平均值均小于 2%。 2 R 使用 Ham 公式计算潜在蒸散发时,每一个子流 域率定期和检验期的 Nash效率系数都达到 70%以 上。而且 41 个流域率定期和检验期的 组成的数据 序列,方差较小,说明使用 Ham 法时,41 个子流域 的月径流模拟精度 波动性小,均处于较高的模拟水 平。Ham 法在率定期和检验期平均RE 均为最小,但 是RE 序列的方差较大,仅次于Tho 法,说明 Ham 法 用于不同子流域时,RE波动性较大。 2 R R2 2 R PM 法在率定期和检验期平均 为84.46%和 84.33%,但是六口流域和县河口流域检验期 小于 70%, 模拟精度略差。Har 方法在率定期和检验期平均 为84.38%和84.18%,平均模拟精度较优,但在六 口流域和县河口流域检验期小于 70%,模拟精度略 差。B-C法在率定期和检验期平均 为83.46%和 83.82%,但是除去同样模拟效果较差的六口和县河口 域外,竹林关流域率定期模拟效果也未能达到70%。 2 R 2 R 2 R 2 R 2 R 5.2. 径流模拟精度比较 图3描绘了使用 5种潜在蒸散发计算公式时,率 定期模型效率系数大于某一个给定 取值的流域的 个数占所有子流域数目的比例,图 4为模型相对误差 大于某一个给定 RE取值的流域的个数占所有子流域 数目的比例。从图中可以看出,对每一个潜在蒸散发 计算公式,两参数月水量平衡模型总体上都达到了较 2 R 流 Figure 3. Percen tage of catchments with the model efficiency greater or equal to the given R2 value for five potential evapotranspiration equations in calibration period 图3. 五种潜在蒸散发公式下率定期模型效率系数大于等于给定R2的流域比例 Figure 4. Percentage of catchments with the volumetric relative error greater or equal to the given RE for five potential evapotranspiration equations in calibration period 图4. 五种潜在蒸散发下率定期流域相对误差大于等于给定 RE的流域比例  熊立华,等:潜在蒸散发公式对汉江流域径流模拟结果的影响 第1卷 · 第4期 Tho 法相对于其它 4种方法是模拟效果最差的,率定 期和检验期平均 最低,同时率定期有 3个流域模拟 效果小于 70%,竹林关流域率定期 2 R50.44%,检 验期有 5个流域模拟效果小于70%。2 RRE 序列方 差也是最大的,说明模拟精度的波动性也最大。可见 使用不同潜在蒸散发计算公式,流域径流模拟结果之 间略有差距。 2 R 仅 和 以模拟效果较好的 Ham 公式为例,图 5和图6 分别描绘了铁锁关流域和两河口流域分别在率定期、 检验期的模拟径流和实测径流过程,从曲线图可以看 到,径流模拟效果良好。 5.3. 实际蒸散发和流域蓄水过程分析 对于径流模拟精度的评定除考虑模型效率系数 和相对误差外,还需考虑模拟的实际蒸散发过程和流 域蓄水过程是否合理。图 7和图 8给出了不同潜在蒸 散发公式下,铁锁关流域在率定期(1972~1976 年)以 及两河口流域在检验期各自的实际蒸散发量和流域 土壤含水量的变化过程曲线。从图中可以看出:流域 实际蒸散发拟合程度较高,实际蒸散发年内变化剧 烈,雨季蒸发量大,旱季蒸发较小;而使用潜在蒸散 发公式时,流域土壤含水量略有差别,但变化趋势相 似,土壤含水量从雨季开始,逐渐增至最大值,从旱 季开始又逐渐降至最小。两者的变化规律符合一般性 规律,变化过程合理。 6. 总结与展望 本文采用 5种不同的潜在蒸散发公式计算流域的 月潜在蒸散发量,将其带入两参数月水量平衡模型, 计算实际蒸散发,同时利用 SCE-UA 算法自动率定模 型参数,较好的实现了汉江流域41个子流域月径流 过程模拟。 结果表明:利用 Ham方法计算潜在蒸散发时,所 有子流域的 Nash 效率系数 在率定期和检验期都达 到70%以上,显示出较高的模拟精度,平均偏差也是 5种不同的潜在蒸散发估计公式中最小的。利用其它 4 种公式计算潜在蒸散发时,个别流域出现了模拟精度 略差的情况,R2小于 70%。其中,使用 Tho 公式模拟 2 R Figure 5. The process of actual and simulated runoff at the Tiesuoguan catchment in calibration period 图5. 铁锁关流域率定期实际径流与模拟径流过程 Figure 6. The process of actual and simulated runoff at the Lianghekou catchment in verification period 图6. 两河口流域检验期实际径流与模拟径流过程 Copyright © 2012 Hanspub 183  熊立华,等:潜在蒸散发公式对汉江流域径流模拟结果的影响 第1卷 · 第4期 0 50 100 150 200 250 1972-11973-1 1974-1 1975-11976-1 1977-1时间 实际蒸散发(mm) 0 200 400 600 800 1000 降水量(mm ) 降水 B-C Har PM Tho Ham 0 40 80 120 160 1972-1 1973-11974-11975-1 1976-11977-1时间 流域土壤含水量(mm) 0 200 400 600 800 1000 降水量(mm) 降水 B-C Har PM Tho Ham Figure 7. The process of actual evapotranspiration and soil water content at the Tiesuoguan catchment for five potential evapotranspiration equations in calibration period 图7. 5种不同潜在蒸散发公式下铁锁关流域率定期实际蒸散发以及流域土壤含水量变化过程 0 50 100 150 200 250 1984-1 1985-1 1986-11987-1 1988-1 1989-1 时间 实际蒸散发(mm) 0 100 200 300 400 500 600 700 降水量(mm) 降水 B-C Har PM Tho Ham 0 50 100 150 200 250 300 350 1984-1 1985-1 1986-1 1987-1 1988-1 1989-1时间 流域土壤含水量(mm ) 0 100 200 300 400 500 600 700 降水量(mm) 降水 B-C Har PM Tho Ha m Figure 8. The process of actual evapotranspiration and soil water content at the Lianghekou catchment for five potential evapotranspiration equations in verification period 图8. 5种不同潜在蒸散发公式下两河口流域检验期实际蒸散发以及流域土壤含水量变化过程 精度最差。尽管使用不同的潜在蒸散发公式,模拟精 度略有差距,但总体而言,两参数模型都成功的模拟 了汉江 41个子流域的月径流过程,对实际蒸散发和 流域蓄水过程的模拟也比较合理。因此,在汉江流域 可以利用潜在蒸散发公式估计实际蒸散发并进行月 径流模拟,其结果精度可靠,能够为流域供水、水资 源合理配置提供依据,对于该流域的中长期水文预 报,也具有一定的参考价值。 参考文献 (References) [1] THORNTHWAITE, C. W., MATHER, J. R. The water balance. Publications in Climatology. Lab. Drexel Institute of Technology, 1955, 8(1): 1-104. [2] PALMER, W. C. Meteorologic drought. US Weather Bureau Re- search Paper, 1965. [3] THOMAS, H. A. Improved methods for national water assess- ment, report, contract WR15249270. Washington DC: US Water Resources Council, 1981. [4] GUO, S. Impact of climate change on hydrological balance and water resources systems in the Dongjiang Basin, China. Model- ing and Management of Sustainable Basin-Scale Water Resources, July 1995 LAHS Publ.No.231, 1995. [5] XIONG, L., GUO, S. A two-parameter monthly water balance model and its application. Journal of Hydrology, 1999, 216(1): 111-123. [6] ALLEY, W. M. On the treatment of evapotranspiration, soil moisture accounting, and aquifer recharge in monthly water bal- ance models. Water Resources Research, 1984, 20(8): 1137-1149. [7] VANDEWIELE, G. L., WIN, N . L. Monthly water balance mod- els for 55 basins in 10 countries. Hydrological Sciences Journal, 1998, 43(5): 687-699. [8] XU, C. Y., SINGH, V. P. A review on monthly water balance models for water resources investig ations. Wate r Resources Ma n- agement, 1998, 12(1): 31-50. [9] 李帅, 熊立华, 万民. 月水量平衡模型的比较研究[J]. 水文, 2011, 31(5): 35-41. LI Shuai, XIONG Lihua and WAN Min. Comparison of monthly water balance models. Journal of China Hydrology, 2011, 31(5): 35-41. (in Chinese) [10] XU, C. Y., SINGH, V. P. Evaluation of three complementary relationship evapotranspiration models by water balance ap- proach to estimate actual regional evapotranspiration in different climatic regions. Journal of Hydrology, 2005, 308(1-4): 105- 121. [11] 秦年秀, 陈喜, 薛显武, 等. 潜在蒸散发量计算公式在贵州省 适用性分析[J]. 水科学进展, 2010, 21(3): 357-363. QIN Nianxiu, CHEN Xi, XUE Xianwu, et al. An applicability study of potential evapotranspiration models in Guizhou Prov- ince. Advances in Water Science, 2010, 21(3): 357-363. (in Chinese) [12] 张晓琳, 熊立华, 林琳, 等. 五种潜在蒸散发方法在汉江流域 的应用[J]. 干旱区地理, 2012, 35(2): 229-237. ZHANG Xiaolin, XIONG Lihua, LIN Lin, et al. The application of five potential evapotranspiration equations in Hanjiang Basin. Arid Land Geography, 2012, 35(2): 229-237. (in Chinese) [13] ALLEN, R. G., PEREIRA, L. S., RAES, D., et al. Crop evapo- transpiration guidelines for computing crop water requirements. FAO Irrigation and Drainage Paper, Rome, 1998: 1-300. [14] 刘晓英, 李玉中, 王庆锁. 几种基于温度的参考作物蒸散量 计算方法评价[J]. 农业工程学报, 2006, 22(6): 12-18. LIU Xiaoying, LI Yuzhong and WANG Qingsuo. Evaluation on several temperature-based methods for estimating reference crop evapotranspiration. Transaction of CSAE, 2006, 22(6): 12-18. (in Chinese) Copyright © 2012 Hanspub 184  熊立华,等:潜在蒸散发公式对汉江流域径流模拟结果的影响 第1卷 · 第4期 [15] 王声峰, 段爱旺, 张展羽. 半干旱地区不同水文年 Hargreaves 和P-M 公式的对比分析[J]. 农业工程学报, 2008, 24(7): 29-33. WANG Shengfeng, DUAN Aiwang and ZHANG Zhanyu. Comparison and analysis of Hargreaves equation and Pen- man-Mon-teith equation during the different hydrological years in the semi-arid region. Transaction of CSAE, 2008, 24(7): 29-33. (in Chinese) [16] XU, C. Y., SINGH, V. P. Evaluation and generalization of tem- perature-based methods for calculating evaporation. Hy drol ogic al Processes, 2001, 15(2): 305-319. [17] PAPADOPOULOU, E., VARANOU, E., BALTAS, E., et al. Estimating potential evapotranspiration and its spatial distribu- tion in Greece using empirical methods. 8th International Con- ference on Environmental Science and Technology, Lemnos Is- land, 8-10 September 2003: 650-658. [18] 唐丽霞, 张志强, 王新杰, 等. 晋西黄土高原丘陵沟壑区清水 河流域径流对土地利用和气候变化的响应[J]. 植物生态学报, 2010, 34(7): 800-810. TANG Lixia, ZHANG Zhiqiang, WANG Xinjie, et al. Stream- flow response to climate and land use changes in Qingshui River watershed in the loess hilly-gully region of Western Shanxi Province, China. Chinese Journal of Plant Ecology, 2010, 34(7): 800-810. (in Chinese) [19] 彭世彰, 徐俊增. 参考作物蒸发蒸腾量计算方法的应用比较 [J]. 灌溉排水学报, 2004, 23(6): 5-9. PENG Shizhang, XU Junzeng. Comparison of reference crop evapotranspiration computing methods. Journal of Irrigation and Drainage, 2004, 23(6): 5-9. (in Chinese) [20] 黄锡荃, 李惠明, 金伯欣. 水文学[M]. 北京: 高等教育出版 社, 1992. HUANG Xiquan, LI Huiming and JIN Boxin. Hydrology. Bei- jing: China Education Press, 1992. (in Chinese) [21] NASH, J. E., SUTCLIFFE, J. V. River flow forecasting through conceptual models. Journal of Hydrology, 1970, 10(3): 282-290. [22] DUAN, Q. Y., GUPTA, V. K. and SOROOSHIAN, S. Shuffled complex evolution approach for effective and efficient global minimization. Journal of Optimization Theory and Application, 1993, 76(3): 501-521. [23] SOROOSHIAN, S., DUAN, Q. Y. and GUPTA, V. K. Optimal use of the SCE-UA global optimization method for calibrating watershed models. Journal of Hydrology, 1994, 158(3-4): 265- 284. Copyright © 2012 Hanspub 185 |