有限理性下不确定参数多目标博弈平衡的稳定性 Stability of Equilibria for Multiobjective Games with Uncertain Parameters under Bounded Rationality

doi:10.12677/ORF.2023.132127

Operations Research and Fuzziology
Vol. 13 No. 02 ( 2023 ), Article ID: 64627 , 16 pages
10.12677/ORF.2023.132127

有限理性下不确定参数多目标博弈平衡的稳定性

陈聪利¹，汤卫^1,2*，王春¹

●How to Cite this Article

¹贵州大学数学与统计学院，贵州贵阳

²贵州开放大学信息工程学院，贵州贵阳

收稿日期：2023年3月6日；录用日期：2023年4月20日；发布日期：2023年4月27日

摘要

本文从有限理性的角度，建立了不确定参数下多目标博弈的有限理性模型，并通过构造特殊的理性函数，证明了在支付函数发生扰动的情况下，该有限理性模型是结构稳定的，并且对弱 $ε$ -Pareto-NS平衡也是鲁棒的。进一步，我们通过具体算例对其平衡的稳定性进行更加直观的验证分析。

关键词

有限理性，多目标博弈，不确定参数，弱Pareto-NS平衡，稳定性

Stability of Equilibria for Multiobjective Games with Uncertain Parameters under Bounded Rationality

Congli Chen¹, Wei Tang^1,2*, Chun Wang¹

¹School of Mathematics and Statistics, Guizhou University, Guiyang Guizhou

²School of Information Engineering, Guizhou Open University, Guiyang Guizhou

Received: Mar. 6^th, 2023; accepted: Apr. 20^th, 2023; published: Apr. 27^th, 2023

ABSTRACT

From the perspective of bounded rationality, this paper establishes a bounded rationality model of multiobjective games with uncertain parameters, and proves that the bounded rationality model is structurally stable and weak $ε$ -Pareto-NS equilibria is robust when the payoff function is disturbed by constructing a special rationality function. Further, the stability of equilibria for the game is verified and analyzed more intuitively by a specific example.

Keywords:Bounded Rationality, Multiobjective Games, Uncertain Parameters, Weak Pareto-NS Equilibria, Stability

This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).

http://creativecommons.org/licenses/by/4.0/

1. 引言

在经典的博弈模型中，局中人被假定为完全理性的，即每个局中人在一定的约束条件下总是能够选出使自己利益最大的策略。然而现实生活中的人并不是完美的，致使这一假设过于理想化。1978年Nobel经济学奖获得者Simon [1] 对该假设提出质疑和批判。Anderlini和Canning [2] 于2001年建立了有限理性抽象模型 $Ψ = (Λ, X, T, R)$ ： $Λ$ 为问题空间， $\forall γ \in Λ$ 表示一个博弈；X表示行为空间， $\forall x \in X$ 是一个策略； $T : Λ \times X \to 2^{X}$ 是可行映射，由T诱导出集值映射 $\bar{t} : Λ \to 2^{X}$ ，其中 $\forall γ \in Λ$ ， $\bar{t} (γ) = {x \in X : x \in T (γ, x)}$ ；集值映射 $\bar{t}$ 的图 $G r a p h (\bar{t}) = {(γ, x) \in Λ \times X : x \in \bar{t} (γ)}$ ， $R : G r a p h (\bar{t}) \to ℜ_{+}$ 为理性函数； $\forall γ \in Λ$ ， $\forall ε \geq 0$ ， $E (γ, ε) = {x \in \bar{t} (γ) : R (γ, x) \leq ε}$ 表示博弈 $γ$ 的 $ε$ -平衡点集，它对应有限理性， $E (γ) = E (γ, 0) = {x \in \bar{t} (γ) :$ $R (γ, x) = 0}$ 表示博弈 $γ$ 的平衡点集，它对应于完全理性。同时假设 $(Λ, ρ)$ 和 $(X, d)$ 均是紧度量空间，集值映射 $\bar{t} : Λ \to 2^{X}$ 紧值且是连续的， $R : G r a p h (\bar{t}) \to ℜ_{+}$ 连续，而 $\forall γ \in Λ$ ， $E (γ) \neq \emptyset$ 。此外，给出该模型 $ε$ -平衡鲁棒和结构稳定的定义，并证明模型 $Ψ$ 对 $ε$ -平衡是鲁棒的当且仅当模型 $Ψ$ 是结构稳定的。由于该模型的假设条件过于苛刻，n人非合作博弈和广义博弈等博弈模型无法满足，导致其应用受到了很大的限制。

俞建等 [3] [4] 将模型 $Ψ$ 的假设条件减弱为： $(Λ, ρ)$ 是完备度量空间， $(X, d)$ 是紧度量空间，集值映射 $\bar{t} : Λ \to 2^{X}$ 是上半连续的， $R : G r a p h (\bar{t}) \to ℜ_{+}$ 是下半连续的，而 $\forall γ \in Λ$ ， $E (γ) \neq \emptyset$ 。这样， $\forall γ \in Λ$ ， $\forall ε \geq 0$ ， $E (γ, ε) = {x \in \bar{t} (γ) : R (γ, x) \leq ε}$ 必是X中的闭集，从而是紧集。进而减弱了 $ε$ -平衡鲁棒和结构稳定成立的条件，并得到相关稳定性与鲁棒性结论。在博弈平衡存在的前提下，俞建等 [5] [6] [7] [8] 对n人非合作博弈、广义博弈、多目标博弈、广义多目标博弈等博弈问题构造了有限理性模型，并得到相应的稳定性结论。此外，王红蕾等 [9] [10] 通过定义理性函数，证明了大多数的最优化问题及多目标最优化问题都是结构稳定的和鲁棒的。

由于现实生活中存在许多的不确定因素，如信息的不完全、气候环境等，在一定程度上影响着策略的选取。1994年，在不确定参数变化范围是已知的假设下，Zhukovskii [11] 首先提出不确定参数下非合作博弈Nash-Slater平衡(简称NS平衡)的概念，并证明了该平衡的存在性。在此基础上，许多学者将不确定参数引入到经典的博弈模型中，提出相应的平衡概念，并得到其存在性及通有稳定性等结论 [12] [13] [14] [15] 。而在博弈过程中，策略选取不仅受到决策环境的影响，还受到局中人有限理性程度的影响，将不确定性和有限理性结合建立的数学模型会更加贴近实际生活。

近年来，已有部分学者从有限理性的角度研究不确定参数下博弈平衡的稳定性，他们基于不确定参数下的博弈模型及其平衡的定义，建立对应的有限理性模型与理性函数，得到其稳定性等结论 [16] [17] [18] 。然而现实生活中局中人的支付函数往往是多目标的，而这方面的研究目前还比较少。因此，我们将建立带有特殊理性函数的不确定参数下多目标博弈有限理性模型，研究不确定参数下多目标博弈平衡的稳定性。进一步，通过算例写出理性函数的具体表达式，同时借助Matlab软件画图来直观体现不确定参数及扰动参数对其平衡稳定性的影响。

2. 预备知识

本文记 $ℜ$ 为实数集或1维实空间， $ℜ^{k}$ 为实k维欧氏空间， $ℜ_{+}$ 为全体正实数构成的集合。

首先介绍不确定参数下多目标博弈模型及其该博弈的弱Pareto-NS平衡的定义，可参见文献 [14] 。

不确定参数下多目标博弈的一般模型 $Γ = (N, K, X_{i}, G_{i}, Y)$ ，其中 $N = {1, 2, \dots, n}$ 是局中人集合， $K = {1, 2, \dots, k}$ 为目标集， $\forall i \in N$ ， $X_{i}$ 是局中人i的策略集，Y是不确定参数集合， $Y \subset ℜ^{p}$ ， $p \geq 1$ ， $G_{i} = (g_{i}^{1}, \dots, g_{i}^{k}) : X \times Y \to ℜ^{k}$ 是局中人i的向量值支付函数，记 $X = \prod_{i = 1}^{n} X_{i}$ ， $X_{- i} = \prod_{j \neq i} X_{j}$ ， $x = (x_{i}, x_{- i}) \in X$ ， $x_{- i} = (x_{1}, \dots, x_{i - 1}, x_{i + 1}, \dots, x_{n}) \in X_{- i}$ 。在该博弈中每个局中人选择各自的策略，最大化自己的支付函数。

定义2.1 $(x^{*}, y^{*}) \in X \times Y$ 称为不确定参数下多目标博弈 $Γ$ 的弱Pareto-NS平衡，若满足

1) $\forall i \in N$ ， $\forall u_{i} \in X_{i}$ ， $G_{i} (u_{i}, x_{- i}^{*}, y^{*}) - G_{i} (x_{i}^{*}, x_{- i}^{*}, y^{*}) \notin i n t ℜ_{+}^{k}$ ；

2) $\forall y \in Y$ ， $G (x^{*}, y^{*}) - G (x^{*}, y) \notin i n t ℜ_{+}^{n \times k}$ ，其中 $G = (G_{1}, \dots, G_{n})$ ， $i n t ℜ_{+}^{n} = {a = (a_{1}, \dots, a_{n}) \in ℜ^{n} | a_{i} > 0, i = 1, 2, \dots, n}$ 。

定义2.2设X，Z是两个度量空间，集值映射 $\tilde{φ} : X \to 2^{Z}$ ， $x \in X$ 。

1) 如果对Z中的任意开集U， $U \supset \tilde{φ} (x)$ (或 $U \cap \tilde{φ} (x) \neq \emptyset$ )，存在x的开邻域 $O (x)$ ，使 $\forall x^{'} \in O (x)$ ，有 $U \supset \tilde{φ} (x^{'})$ (或 $U \cap \tilde{φ} (x^{'}) \neq \emptyset$ )，则称集值映射 $\tilde{φ}$ 在x上是上半连续的(或下半连续的)；

2) 如果集值映射 $\tilde{φ}$ 在x即上半连续又下半连续，则称集值映射 $\tilde{φ}$ 在x是连续的；

3) 如果 $\forall x \in X$ ，集值映射 $\tilde{φ}$ 在x是连续的(或上半连续的，或下半连续的)，则称集值映射 $\tilde{φ}$ 在X上是连续的(或上半连续的，或下半连续的)。

Yu和Yu在文献 [3] 中给出如下定义和稳定性结论。

定义2.3 $\forall γ \in (Λ, ρ)$ ，若 $\forall δ > 0$ ， $\exists \bar{ε} > 0$ ，当 $ε < \bar{ε}$ ， $ρ (γ, γ^{'}) < \bar{ε}$ 时，有 $h (E (γ^{'}, ε), E (γ^{'})) < δ$ ，则称 $Ψ$ 在 $γ$ 对 $ε$ -平衡是鲁棒的，其中h是X上的Hausdorff距离。

定义2.4如果平衡映射 $E : Λ \to 2^{X}$ 在 $γ \in Λ$ 是连续的，则称 $Ψ$ 在 $γ$ 是结构稳定的。

引理2.1设 $(Λ, ρ)$ 为完备度量空间， $(X, d)$ 为紧度量空间， $\bar{t} : Λ \to 2^{X}$ 是上半连续的且 $\forall γ \in Λ$ ， $\bar{t} (γ)$ 是非空紧集， $R : G r a p h (\bar{t}) \to ℜ_{+}$ 是下半连续的且 $\forall γ \in Λ$ ， $E (γ) \neq \emptyset$ ，则

1) 平衡映射 $E : Λ \to 2^{X}$ 是一个usco映射，即 $\forall γ \in Λ$ ，E在 $γ$ 是上半连续的，且 $E (γ)$ 是紧集；

2) 存在 $Λ$ 中的一个稠密剩余集Q，使 $\forall γ \in Q$ ， $Ψ$ 在 $γ$ 是结构稳定的；

3) 如果 $Ψ$ 在 $γ \in Λ$ 是结构稳定的，则 $Ψ$ 在 $γ$ 对 $ε$ -平衡是鲁棒的；

4) $\forall γ \in Q$ ， $\forall γ^{m} \to γ$ ， $\forall ε^{m} \to 0$ ，有 $h (E (γ^{m}, ε^{m}), E (γ)) \to 0$ ，其中h是X上的Hausdorff距离；

5) 如果 $γ \in Λ$ ，且 $E (γ)$ 是单点集，则 $Ψ$ 在 $γ$ 是结构稳定的，在 $γ$ 对 $ε$ -平衡也是鲁棒的。

引理2.2设X，C，Z是三个度量空间，其中Z是紧的， ${A^{m}}$ 是X中的一列非空紧集， $h (A^{m}, A) \to 0$ ，其中h是X上的Hausdorff距离，A是X中的一个非空紧集， $\forall m = 1, 2, 3, \dots$ ， $μ^{m} : X \times C \times Z \to ℜ$ 连续， $\sup_{(x, c, z) \in X \times C \times Z} | μ^{m} (x, c, z) - μ (x, c, z) | \to 0$ ，其中 $μ$ 为 $X \times C \times Z$ 上一连续函数， ${c^{m}}$ 是C中的一个序列，

$c^{m} \to c$ ，则 $\max_{w \in A^{m}} \min_{z \in Z} μ^{m} (w, c^{m}, z) \to \max_{w \in A} \min_{z \in Z} μ (w, c, z)$ 。

3. 不确定参数下多目标博弈平衡的稳定性

在本节中，假设 $(X_{i}, d_{i})$ 和 $(Y, d^{'})$ 为非空紧度量空间，函数空间 $Λ$ 定义如下：

$Λ = {Φ = (G_{1}, \dots, G_{n}) : X \times Y \to ℜ^{n \times k} | \forall i \in N, G_{i} : X \times Y \to ℜ^{k}$ 是连续的，存在 $(x^{*}, y^{*}) \in X \times Y$ ，使 $\forall i \in N$ ， $\forall u_{i} \in X_{i}$ ，有 $G_{i} (u_{i}, x_{- i}^{*}, y^{*}) - G_{i} (x_{i}^{*}, x_{- i}^{*}, y^{*}) \notin i n t ℜ_{+}^{k}$ ； $G (x^{*}, y^{*}) - G (x^{*}, y) \notin i n t ℜ_{+}^{n \times k}$ ， $\forall y \in Y}$ 。

$\forall Φ \in Λ$ ，用 $E (Φ)$ 表示不确定参数下多目标博弈 $Φ$ 的所有弱Pareto-NS平衡的集合，由 $Λ$ 的定义知， $E (Φ) \neq \emptyset$ 。

$\forall Φ = (G_{1}, \dots, G_{n})$ ， $\tilde{Φ} = ({\tilde{G}}_{1}, \dots, {\tilde{G}}_{n}) \in Λ$ ，定义距离如下

$ρ (Φ, \tilde{Φ}) = \sum_{i = 1}^{n} \max_{(x, y) \in X \times Y} ‖ G_{i} (x, y) - {\tilde{G}}_{i} (x, y) ‖$ 。

引理3.1 $(Λ, ρ)$ 是一个完备度量空间。

证明设 ${U^{m} = (U_{1}^{m}, U_{2}^{m}, \dots, U_{n}^{m})}$ 是 $Λ$ 中的任意一个Cauchy列，即 $\forall ε > 0$ ，存在正整数 $m_{0}$ ，使 $\forall m, p \geq m_{0}$ ，有

$ρ (U^{m}, U^{p}) = \sum_{i = 1}^{n} \max_{(x, y) \in X \times Y} ‖ U_{i}^{m} (x, y) - U_{i}^{p} (x, y) ‖ < \frac{ε}{2 n}$ 。

从而， $\forall i \in N$ ， $\forall (x, y) \in X \times Y$ ，都有

$‖ U_{i}^{m} (x, y) - U_{i}^{p} (x, y) ‖ < \frac{ε}{2 n}$ ，

这说明 ${U_{i}^{m} (x, y)}$ 是 $ℜ^{k}$ 中的Cauchy列，由 $ℜ^{k}$ 的完备性知，存在 $U_{i} : X \times Y \to ℜ^{k}$ ，使 $\lim_{m \to \infty} U_{i}^{m} (x, y) = U_{i} (x, y)$ 。

令 $m \to \infty$ ，由上式得

$‖ U_{i}^{p} (x, y) - U_{i} (x, y) ‖ < \frac{ε}{2 n}$ ， $\forall (x, y) \in X \times Y$ ，

且易知 $U_{i}$ 在 $X \times Y$ 连续，故 $\max_{(x, y) \in X \times Y} ‖ U_{i}^{p} (x, y) - U_{i} (x, y) ‖ < \frac{ε}{2 n}$ ，进而有

$\sum_{i = 1}^{n} \max_{(x, y) \in X \times Y} ‖ U_{i}^{p} (x, y) - U_{i} (x, y) ‖ < \frac{ε}{2}$ 。

对 $\forall m, p \geq m_{0}$ ，有

$\begin{matrix} ρ (U^{m}, U) = \sum_{i = 1}^{n} \max_{(x, y) \in X \times Y} ‖ U_{i}^{m} (x, y) - U_{i} (x, y) ‖ \\ \leq \sum_{i = 1}^{n} \max_{(x, y) \in X \times Y} ‖ U_{i}^{m} (x, y) - U_{i}^{p} (x, y) ‖ + \sum_{i = 1}^{n} \max_{(x, y) \in X \times Y} ‖ U_{i}^{p} (x, y) - U_{i} (x, y) ‖ \\ < \frac{ε}{2 n} + \frac{ε}{2} < ε 。 \end{matrix}$

因此， $U^{m} \to U = (U_{1}, U_{2}, \dots, U_{n})$ 。

因 $U^{m} \in Λ$ ， $\exists (x^{m}, y^{m}) \in X \times Y$ ，使

$U_{i}^{m} (u_{i}, x_{- i}^{m}, y^{m}) - U_{i}^{m} (x_{i}^{m}, x_{- i}^{m}, y^{m}) \notin i n t ℜ_{+}^{k}$ ， $\forall i \in N$ ， $\forall u_{i} \in X_{i}$ ；

$U^{m} (x^{m}, y^{m}) - U^{m} (x^{m}, y) \notin i n t ℜ_{+}^{n \times k}$ ， $\forall y \in Y$ 。

又因 $X \times Y$ 是紧集，不妨设 $(x^{m}, y^{m}) \to (x^{*}, y^{*}) \in X \times Y$ 。 $\forall m \geq m_{0}$ ，因

$\begin{array}{l} ‖ U_{i}^{m} (u_{i}, x_{- i}^{m}, y^{m}) - U_{i} (u_{i}, x_{- i}^{*}, y^{*}) ‖ \\ \leq ‖ U_{i}^{m} (u_{i}, x_{- i}^{m}, y^{m}) - U_{i} (u_{i}, x_{- i}^{m}, y^{m}) ‖ + ‖ U_{i} (u_{i}, x_{- i}^{m}, y^{m}) - U_{i} (u_{i}, x_{- i}^{*}, y^{*}) ‖ \\ \leq ρ (U^{m}, U) + ‖ U_{i} (u_{i}, x_{- i}^{m}, y^{m}) - U_{i} (u_{i}, x_{- i}^{*}, y^{*}) ‖, \end{array}$

由于 $U_{i}$ 在 $X \times Y$ 上是连续的，可得 $U_{i}^{m} (u_{i}, x_{- i}^{m}, y^{m}) \to U_{i} (u_{i}, x_{- i}^{*}, y^{*})$ 。

同理可得， $U_{i}^{m} (x_{i}^{m}, x_{- i}^{m}, y^{m}) \to U_{i} (x_{i}^{*}, x_{- i}^{*}, y^{*})$ ，进而 $\forall i \in N$ ，有 $U^{m} (x^{m}, y^{m}) \to U (x^{*}, y^{*})$ 。又 $U_{i}$ 在 $X \times Y$ 上是连续的，且 $x^{m} \to x^{*}$ ，得 $U (x^{m}, y) \to U (x^{*}, y)$ 。

从而， $\forall i \in N$ ， $\forall u_{i} \in X_{i}$ ， $U_{i} (u_{i}, x_{- i}^{*}, y^{*}) - U_{i} (x_{i}^{*}, x_{- i}^{*}, y^{*}) \notin i n t ℜ_{+}^{k}$ ； $\forall y \in Y$ ， $U (x^{*}, y^{*}) - U (x^{*}, y) \notin i n t ℜ_{+}^{n \times k}$ 。综上可得 $U \in Λ$ ， $(Λ, ρ)$ 是一个完备度量空间。 □

下面，我们构造不确定参数下多目标博弈的有限理性模型 $ϒ = (Λ, X, Y, J, R)$ ，其中 $Λ$ 是博弈空间，

每个 $Φ \in Λ$ 表示不确定参数下多目标博弈， $X = \prod_{i = 1}^{n} X_{i}$ 为策略集，Y是不确定参数集， $J : Λ \times X \times Y \to 2^{X \times Y}$

为可行映射，由J诱导出行为映射 $τ : Λ \to 2^{X \times Y}$ 。定义 $J (Φ, x, y) = X \times Y$ ，则对 $\forall Φ \in Λ$ ，有

$τ (Φ) = {(x, y) \in X \times Y : (x, y) \in J (Φ, x, y)} = X \times Y$ 。

显然， $τ$ 连续且 $τ (Φ)$ 为非空紧集。定义理性函数 $R : Λ \times X \times Y \to ℜ_{+}$ 为

$R (Φ, x, y) = \sum_{i = 1}^{n} \max_{u_{i} \in X_{i}} \min_{{‖ λ ‖}_{1} =1, λ \in ℜ_{+}^{k}} 〈 λ, G_{i} (u_{i}, x_{- i}, y) - G_{i} (x_{i}, x_{- i}, y) 〉 + \max_{v \in Y} \min_{{‖ z ‖}_{1} =1, z \in ℜ_{+}^{n \times k}} 〈 z, G (x, y) - G (x, v) 〉$ ，

其中， ${‖ λ ‖}_{1}$ ， ${‖ z ‖}_{1}$ 分别表示k维和 $n \times k$ 维欧氏空间中的曼哈顿距离，即 ${‖ λ ‖}_{1}$ ， ${‖ z ‖}_{1}$ 分别为 $λ$ 向量和z向量各个元素绝对值之和。

以下我们给出理性函数 $R (Φ, x, y)$ 的一些相关结果。

引理3.2 (1) $\forall Φ \in Λ$ ， $\forall (x, y) \in X \times Y$ ，有 $R (Φ, x, y) \geq 0$ ；

(2) $R (Φ, x, y) = 0$ 当且仅当 $(x, y) \in E (Φ)$ 。

证明(1) $\forall Φ \in Λ$ ， $\forall (x, y) \in X \times Y$ ，

$R (Φ, x, y) \geq \sum_{i = 1}^{n} \min_{{‖ λ ‖}_{1} = 1, λ \in ℜ_{+}^{k}} 〈 λ, G_{i} (x_{i}, x_{- i}, y) - G_{i} (x_{i}, x_{- i}, y) 〉 + \min_{{‖ z ‖}_{1} = 1, z \in ℜ_{+}^{n \times k}} 〈 z, G (x, y) - G (x, y) 〉 = 0$ 。

(2) 如果 $R (Φ, x, y) = 0$ ，那么

$\sum_{i = 1}^{n} \max_{u_{i} \in X_{i}} \min_{{‖ λ ‖}_{1} = 1, λ \in ℜ_{+}^{k}} 〈 λ, G_{i} (u_{i}, x_{- i}, y) - G_{i} (x_{i}, x_{- i}, y) 〉 = 0$ ， (3.1)

$\max_{v \in Y} \min_{{‖ z ‖}_{1} = 1, z \in ℜ_{+}^{n \times k}} 〈 z, G (x, y) - G (x, v) 〉 = 0$ 。 (3.2)

由(3.1)式， $\forall i \in N$ ， $\forall u_{i} \in X_{i}$ ，有

$\min_{{‖ λ ‖}_{1} = 1, λ \in ℜ_{+}^{k}} 〈 λ, G_{i} (u_{i}, x_{- i}, y) - G_{i} (x_{i}, x_{- i}, y) 〉 \leq 0$ 。 (3.3)

如果 $(x, y)$ 不满足定义2.1条件(1)，则 $\exists i_{0} \in N$ ， $\exists u_{i_{0}} \in X_{i_{0}}$ ，使

$G_{i_{0}} (u_{i_{0}}, x_{- i_{0}}, y) - G_{i_{0}} (x_{i_{0}}, x_{- i_{0}}, y) \in i n t ℜ_{+}^{k}$ 。

对 $\forall λ \in {λ \in ℜ_{+}^{k} : {‖ λ ‖}_{1} = 1}$ ，有

$〈 λ, G_{i_{0}} (u_{i_{0}}, x_{- i_{0}}, y) - G_{i_{0}} (x_{i_{0}}, x_{- i_{0}}, y) 〉 > 0$ ，

由于 ${λ \in ℜ_{+}^{k} : {‖ λ ‖}_{1} = 1}$ 是紧的，则

$\min_{{‖ λ ‖}_{1} = 1, λ \in ℜ_{+}^{k}} 〈 λ, G_{i_{0}} (u_{i_{0}}, x_{- i_{0}}, y) - G_{i_{0}} (x_{i_{0}}, x_{- i_{0}}, y) 〉 > 0$ ，

这与(3.3)式矛盾，故 $(x, y)$ 满足定义2.1条件(1)。

另一方面，如果 $(x, y)$ 不满足定义2.1条件(2)，则 $\exists v_{0} \in Y$ ，使

$G (x, y) - G (x, v_{0}) \in i n t ℜ_{+}^{n \times k}$ 。

对 $\forall z \in {z \in ℜ_{+}^{n \times k} : {‖ z ‖}_{1} = 1}$ ，有 $〈 z, G (x, y) - G (x, v_{0}) 〉 > 0$ 。

由于 ${z \in ℜ_{+}^{n \times k} : {‖ z ‖}_{1} = 1}$ 是紧的，则有

$\max_{v \in Y} \min_{{‖ z ‖}_{1} = 1, z \in ℜ_{+}^{n \times k}} 〈 z, G (x, y) - G (x, v) 〉 \geq \min_{{‖ z ‖}_{1} = 1, z \in ℜ_{+}^{n \times k}} 〈 z, G (x, y) - G (x, v_{0}) 〉 > 0$ ，

这与(3.2)式矛盾，故 $(x, y)$ 满足定义2.1条件(2)。从而 $(x, y) \in E (Φ)$ 。

反之，如果 $(x, y) \in E (Φ)$ ，则有

$G_{i} (u_{i}, x_{- i}, y) - G_{i} (x_{i}, x_{- i}, y) \notin i n t ℜ_{+}^{k}$ ， $\forall i \in N$ ， $\forall u_{i} \in X_{i}$ ； (3.4)

$G (x, y) - G (x, v) \notin i n t ℜ_{+}^{n \times k}$ ， $\forall v \in Y$ 。 (3.5)

由(3.4)式， $\forall j = 1, 2, \dots, k$ ，令 $\tilde{J} = {j : g_{i}^{j} (u_{i}, x_{- i}, y) - g_{i}^{j} (x_{i}, x_{- i}, y) \leq 0}$ ，则 $\tilde{J} \neq \emptyset$ 。此时，取 $j_{0} \in \tilde{J}$ ，令 $λ^{0} = (λ_{1}^{0}, \dots, λ_{k}^{0})$ ，其中 $λ_{j_{0}}^{0} = 1$ ， $λ_{j}^{0} = 0 (j \neq j_{0})$ ，则 $λ^{0} \in {λ \in ℜ_{+}^{k} : {‖ λ ‖}_{1} = 1}$ ，有

$\begin{array}{l} \min_{{‖ λ ‖}_{1} = 1, λ \in ℜ_{+}^{k}} 〈 λ, G_{i} (u_{i}, x_{- i}, y) - G_{i} (x_{i}, x_{- i}, y) 〉 \leq 〈 λ^{0}, G_{i} (u_{i}, x_{- i}, y) - G_{i} (x_{i}, x_{- i}, y) 〉 \\ = \sum_{j = 1}^{k} λ_{j}^{0} [g_{i}^{j} (u_{i}, x_{- i}, y) - g_{i}^{j} (x_{i}, x_{- i}, y)] = λ_{j_{0}}^{0} [g_{i}^{j_{0}} (u_{i}, x_{- i}, y) - g_{i}^{j_{0}} (x_{i}, x_{- i}, y)] \leq 0, \end{array}$

故 $\sum_{i = 1}^{n} \max_{u_{i} \in X_{i}} \min_{{‖ λ ‖}_{1} = 1, λ \in ℜ_{+}^{k}} 〈 λ, G_{i} (u_{i}, x_{- i}, y) - G_{i} (x_{i}, x_{- i}, y) 〉 \leq 0$ 。

由结论(1)，得 $\sum_{i = 1}^{n} \max_{u_{i} \in X_{i}} \min_{{‖ λ ‖}_{1} = 1, λ \in ℜ_{+}^{k}} 〈 λ, G_{i} (u_{i}, x_{- i}, y) - G_{i} (x_{i}, x_{- i}, y) 〉 \geq 0$ 。

从而，得

$\sum_{i = 1}^{n} \max_{u_{i} \in X_{i}} \min_{{‖ λ ‖}_{1} = 1, λ \in ℜ_{+}^{k}} 〈 λ, G_{i} (u_{i}, x_{- i}, y) - G_{i} (x_{i}, x_{- i}, y) 〉 = 0$ 。

由(3.5)式， $\forall i \in N$ ，令 $\bar{J} (v) = {i : G_{i} (x, y) - G_{i} (x, v) \leq 0}$ ，则 $\bar{J} (v) \neq \emptyset$ 。取 $i_{0} \in \bar{J} (v)$ ，令 $z^{0} = (z_{1}^{0}, \dots, z_{n}^{0})$ ，其中 $z_{i_{0}}^{0} = 1, z_{i}^{0} = 0 (i \neq i_{0})$ ，则 $z^{0} \in {z \in ℜ_{+}^{n \times k} : {‖ z ‖}_{1} = 1}$ ，有

$\begin{array}{l} \min_{{‖ z ‖}_{1} = 1, z \in ℜ_{+}^{n \times k}} 〈 z, G (x, y) - G (x, v) 〉 \leq 〈 z^{0}, G (x, y) - G (x, v) 〉 \\ = \sum_{i = 1}^{n} z_{i}^{0} [G_{i} (x, y) - G_{i} (x, v)] = z_{i_{0}}^{0} [G_{i_{0}} (x, y) - G_{i_{0}} (x, v)] \leq 0. \end{array}$

故 $\max_{v \in Y} \min_{{‖ z ‖}_{1} = 1, z \in ℜ_{+}^{n \times k}} 〈 z, G (x, y) - G (x, v) 〉 \leq 0$ 。

又由结论(1)，得 $\max_{v \in Y} \min_{{‖ z ‖}_{1} = 1, z \in ℜ_{+}^{n \times k}} 〈 z, G (x, y) - G (x, v) 〉 \geq 0$ 。

进而有

$\max_{v \in Y} \min_{{‖ z ‖}_{1} = 1, z \in ℜ_{+}^{n \times k}} 〈 z, G (x, y) - G (x, v) 〉 = 0$ 。

综上可得， $R (Φ, x, y) = 0$ 。 □

引理3.3 $R (Φ, x, y)$ 在 $Λ \times X \times Y$ 上是连续的。

证明 $\forall Φ^{m} = (G_{1}^{m}, \dots, G_{n}^{m}) \in Λ$ ， $Φ^{m} \to Φ = (G_{1}, \dots, G_{n})$ ， $\forall (x^{m}, y^{m}) \in X \times Y$ ，且 $(x^{m}, y^{m}) \to (x, y)$ ，我们要证 $R (Φ^{m}, x^{m}, y^{m}) \to R (Φ, x, y)$ 。

$\forall i \in N$ ， $\forall m = 1, 2, 3, \dots$ ，令

$φ_{i} (u_{i}, x, y, λ) = 〈 λ, G_{i} (u_{i}, x_{- i}, y) - G_{i} (x_{i}, x_{- i}, y) 〉$ ，

$φ_{i}^{m} (u_{i}, x^{m}, y^{m}, λ) = 〈 λ, G_{i}^{m} (u_{i}, x_{- i}^{m}, y^{m}) - G_{i}^{m} (x_{i}^{m}, x_{- i}^{m}, y^{m}) 〉$ ，

$ψ (x, y, v, z) = 〈 z, G (x, y) - G (x, v) 〉$ ， $ψ^{m} (x^{m}, y^{m}, v, z) = 〈 z, G^{m} (x^{m}, y^{m}) - G^{m} (x^{m}, v) 〉$ ，

则 $φ_{i}$ ， $φ_{i}^{m}$ 在 $X \times Y \times W_{1}$ 上是连续的， $ψ$ ， $ψ^{m}$ 在 $X \times Y \times W_{2}$ 上是连续的，其中 $W_{1} = {λ \in ℜ_{+}^{k} : {‖ λ ‖}_{1} = 1}$ ， $W_{2} = {z \in ℜ_{+}^{n \times k} : {‖ z ‖}_{1} = 1}$ 都是紧集。

$\forall i \in N$ ， $\forall (u_{i}, x, y, λ) \in X \times Y \times W_{1}$ ，由于 $Φ^{m} \to Φ$ ，则对 $\forall ε > 0$ ，存在正整数 $m_{1}$ ，使 $\forall m \geq m_{1}$ ，有

$\begin{array}{l} | φ_{i}^{m} (u_{i}, x, y, λ) - φ_{i} (u_{i}, x, y, λ) | \\ = | 〈 λ, G_{i}^{m} (u_{i}, x_{- i}, y) - G_{i}^{m} (x_{i}, x_{- i}, y) 〉 - 〈 λ, G_{i} (u_{i}, x_{- i},, y) - G_{i} (x_{i}, x_{- i}, y) 〉 | \\ \leq | 〈 λ, G_{i}^{m} (u_{i}, x_{- i}, y) - G_{i} (u_{i}, x_{- i}, y) 〉 | + | 〈 λ, G_{i}^{m} (x_{i}, x_{- i}, y) - G_{i} (x_{i}, x_{- i}, y) 〉 | \\ \leq {‖ λ ‖}_{1} ‖ G_{i}^{m} (u_{i}, x_{- i}, y) - G_{i} (u_{i}, x_{- i}, y) ‖ + {‖ λ ‖}_{1} ‖ G_{i}^{m} (x_{i}, x_{- i}, y) - G_{i} (x_{i}, x_{- i}, y) ‖ \\ \leq 2 ρ (Φ^{m}, Φ) \to 0, \end{array}$

得

$\max_{(u_{i}, x, y, λ) \in X \times Y \times W_{1}} | φ_{i}^{m} (u_{i}, x, y, λ) - φ_{i} (u_{i}, x, y, λ) | \to 0$ 。

因 $X_{i}$ ， $W_{1}$ 是紧集，且 $(x^{m}, y^{m}) \to (x, y)$ ，由引理2.2，可得

$\max_{u_{i} \in X_{i}} \min_{{‖ λ ‖}_{1} = 1, λ \in ℜ_{+}^{k}} φ_{i}^{m} (u_{i}, x^{m}, y^{m}, λ) \to \max_{u_{i} \in X_{i}} \min_{{‖ λ ‖}_{1} = 1, λ \in ℜ_{+}^{k}} φ_{i} (u_{i}, x, y, λ)$ ，

进而有，

$\sum_{i = 1}^{n} \max_{u_{i} \in X_{i}} \min_{{‖ λ ‖}_{1} = 1, λ \in ℜ_{+}^{k}} φ_{i}^{m} (u_{i}, x^{m}, y^{m}, λ) \to \sum_{i = 1}^{n} \max_{u_{i} \in X_{i}} \min_{{‖ λ ‖}_{1} = 1, λ \in ℜ_{+}^{k}} φ_{i} (u_{i}, x, y, λ)$ 。

另一方面， $\forall i \in N$ ，由于 $Φ^{m} \to Φ$ ，则对 $\forall ε > 0$ ，存在正整数 $m_{2}$ ， $\forall m \geq m_{2}$ ，有

$‖ G^{m} (x^{m}, y^{m}) - G (x^{m}, y^{m}) ‖ < \frac{ε}{4}$ 和 $‖ G^{m} (x^{m}, v) - G (x^{m}, v) ‖ < \frac{ε}{4}$ 同时成立。

又 $Φ$ 在 $X \times Y$ 是连续的，且 $(x^{m}, y^{m}) \to (x, y)$ ， $\forall ε > 0$ ，存在正整数 $m_{3}$ ， $\forall m \geq m_{3}$ ，有

$‖ G (x^{m}, y^{m}) - G (x, y) ‖ < \frac{ε}{4}$ 和 $‖ G (x^{m}, v) - G (x, v) ‖ < \frac{ε}{4}$ 同时成立。

取 $M_{1} = \max {m_{1}, m_{2}}$ ， $\forall m \geq M_{1}$ ，有

$\begin{array}{l} | ψ^{m} (x^{m}, y^{m}, v, z) - ψ (x, y, v, z) | \\ = | 〈 z, G^{m} (x^{m}, y^{m}) - G^{m} (x^{m}, v) 〉 - 〈 z, G (x, y) - G (x, v) 〉 | \\ \leq | 〈 z, G^{m} (x^{m}, y^{m}) - G (x, y) 〉 | + | 〈 z, G^{m} (x^{m}, v) - G (x, v) 〉 | \\ \leq {‖ z ‖}_{1} ‖ G^{m} (x^{m}, y^{m}) - G (x^{m}, y^{m}) ‖ + {‖ z ‖}_{1} ‖ G (x^{m}, y^{m}) - G (x, y) ‖ \\ + {‖ z ‖}_{1} ‖ G^{m} (x^{m}, v) - G (x^{m}, v) ‖ + {‖ z ‖}_{1} ‖ G (x^{m}, v) - G (x, v) ‖ < ε 。 \end{array}$

因Y， $W_{2}$ 是紧集，由引理2.2，可得

$\max_{v \in Y} \min_{{‖ z ‖}_{1} = 1, z \in ℜ_{+}^{n \times k}} ψ^{m} (x^{m}, y^{m}, v, z) \to \max_{v \in Y} \min_{{‖ z ‖}_{1} = 1, z \in ℜ_{+}^{n \times k}} ψ (x, y, v, z)$ 。

从而，

$R (Φ^{m}, x^{m}, y^{m}) = \sum_{i = 1}^{n} \max_{u_{i} \in X_{i}} \min_{{‖ λ ‖}_{1} = 1, λ \in ℜ_{+}^{k}} φ_{i}^{m} (u_{i}, x^{m}, y^{m}, λ) + \max_{v \in Y} \min_{{‖ z ‖}_{1} = 1, z \in ℜ_{+}^{n \times k}} ψ^{m} (x^{m}, y^{m}, v, z)$

$\to \sum_{i = 1}^{n} \max_{u_{i} \in X_{i}} \min_{{‖ λ ‖}_{1} = 1, λ \in ℜ_{+}^{k}} φ_{i} (u_{i}, x, y, λ) + \max_{v \in Y} \min_{{‖ z ‖}_{1} = 1, z \in ℜ_{+}^{n \times k}} ψ (x, y, v, z) = R (Φ, x, y)$ 。 □

注3.1 $\forall ε \geq 0$ ， $\forall Φ \in Λ$ ， $E (Φ, ε) = {(x, y) \in τ (Φ) : R (Φ, x, y) \leq ε}$ 定义为不确定参数下多目标博弈 $Φ$ 的弱 $ε$ -Pareto-NS平衡集，它描述了不确定参数下多目标博弈中的有限理性。特别地，由引理3.2 (2)可知，当 $ε = 0$ 时， $E (Φ)$ 为博弈 $Φ$ 的弱Pareto-NS平衡集，它刻画了不确定参数下多目标博弈中的完全理性。

定理3.1对不确定参数下多目标博弈的有限理性模型 $ϒ = (Λ, X, Y, J, R)$ ，以下结论成立。

1) 博弈 $Φ$ 的弱Pareto-NS平衡映射 $E : Λ \to 2^{X \times Y}$ 是一个usco映射；

2) 存在 $Λ$ 中的一个稠密剩余集Q，使 $\forall Φ \in Q$ ， $ϒ$ 在 $Φ$ 是结构稳定的；

3) 如果 $ϒ$ 在 $Φ \in Λ$ 是结构稳定的，则 $ϒ$ 在 $Φ$ 对弱 $ε$ -Pareto-NS平衡是鲁棒的；

4) $\forall Φ \in Q$ ， $\forall Φ^{m} \to Φ$ ， $\forall ε^{m} \to 0$ ，有 $\tilde{h} (E (Φ^{m}, ε^{m}), E (Φ)) \to 0$ ，其中 $\tilde{h}$ 是 $X \times Y$ 上的Hausdorff距离；

5) 如果 $Φ \in Λ$ ，且 $E (Φ)$ 是单点集，则 $ϒ$ 在 $Φ$ 是结构稳定的，在 $Φ$ 对弱 $ε$ -Pareto-NS平衡也是鲁棒的。

证明 $(Λ, ρ)$ 是完备度量空间， $X \times Y$ 是紧集， $τ : Λ \to 2^{X \times Y}$ 是上半连续的， $\forall Φ \in Λ$ ， $E (Φ) \neq \emptyset$ ，且 $τ (Φ)$ 是非空紧集。由引理3.3知， $R : Λ \times X \times Y \to ℜ_{+}$ 是下半连续的，故 $ϒ$ 满足引理2.1的所有假设条件，因此引理2.1的结论对 $ϒ$ 也全成立。 □

4. 算例

下面，我们通过算例进一步详细说明本文主要结果定理3.1，即有限理性下不确定参数多目标博弈平衡的稳定性。

例4.1我们考虑二人二策略不确定参数下双目标博弈 $Φ^{'}$ ，局中人集合 $N = {1, 2}$ ，纯策略集 ${1, 2}$ ，局中人1和2的混合策略集分别为 $X_{1} = {x_{1} | 0 \leq x_{1} \leq 1}$ ， $X_{2} = {x_{2} | 0 \leq x_{2} \leq 1}$ ，其中 $x_{1}$ 表示局中人1选择策略1的概率， $x_{2}$ 表示局中人2选择策略1的概率，记 $x^{T} = (x_{1}, 1 - x_{1})$ ， $t^{T} = (x_{2}, 1 - x_{2})$ ，目标集 $K = {1, 2}$ ，目标1和2对应的支付矩阵分别为 $A_{1}$ 和 $A_{2}$ ，且

$A_{1} = (\begin{matrix} a_{11}^{1} & a_{12}^{1} \\ a_{21}^{1} & a_{22}^{1} \end{matrix})$ ， $A_{2} = (\begin{matrix} a_{11}^{2} & a_{12}^{2} \\ a_{21}^{2} & a_{22}^{2} \end{matrix})$ ，

$A_{1}$ ， $A_{2}$ 为严格对角占优对称矩阵，且 $A_{1}, A_{2} \in ℜ_{+}^{2 \times 2}$ 。不确定参数集 $Y = [0, 1]$ ， $\forall y \in Y$ ，则局中人1，2的期望支付函数分别为

$G_{1} (x_{1}, x_{2}, y) = [g_{1}^{1} (x_{1}, x_{2}, y), g_{1}^{2} (x_{1}, x_{2}, y)] = [x^{T} A_{1} t + y, x^{T} A_{2} t + 2 y]$ ；

$G_{2} (x_{1}, x_{2}, y) = [g_{2}^{1} (x_{1}, x_{2}, y), g_{2}^{2} (x_{1}, x_{2}, y)] = [t^{T} A_{1} x + 2 y, t^{T} A_{2} x + y]$ 。

设 $(x^{*}, y^{*})$ 为博弈 $Φ^{'}$ 的弱Pareto-NS平衡，那么

$G_{1} (x_{1}, x_{2}^{*}, y^{*}) - G_{1} (x_{1}^{*}, x_{2}^{*}, y^{*}) = [(x^{T} - x^{* T}) A_{1} t^{*}, (x^{T} - x^{* T}) A_{2} t^{*}] \notin i n t ℜ_{+}^{2}$ ， $\forall x_{1} \in X_{1}$ ；

$G_{2} (x_{1}^{*}, x_{2}, y^{*}) - G_{2} (x_{1}^{*}, x_{2}^{*}, y^{*}) = [(t^{T} - t^{* T}) A_{1} x^{*}, (t^{T} - t^{* T}) A_{2} x^{*}] \notin i n t ℜ_{+}^{2}$ ， $\forall x_{2} \in X_{2}$ ；

$G (x^{*}, y^{*}) - G (x^{*}, y) = [y^{*} - y, 2 y^{*} - 2 y, 2 y^{*} - 2 y, y^{*} - y] \notin i n t ℜ_{+}^{4}$ ， $\forall y \in Y$ 。

不妨设 $\frac{a_{22}^{2} - a_{21}^{2}}{a_{11}^{2} + a_{22}^{2} - a_{12}^{2} - a_{21}^{2}} \leq \frac{a_{22}^{1} - a_{21}^{1}}{a_{11}^{1} + a_{22}^{1} - a_{12}^{1} - a_{21}^{1}}$ ，可得该博弈的弱Pareto-NS平衡集为

${(x^{*}, y^{*})} = {(x, y) \in X \times Y | \frac{a_{22}^{2} - a_{21}^{2}}{a_{11}^{2} + a_{22}^{2} - a_{12}^{2} - a_{21}^{2}} \leq x_{1}, x_{2} \leq \frac{a_{22}^{1} - a_{21}^{1}}{a_{11}^{1} + a_{22}^{1} - a_{12}^{1} - a_{21}^{1}}, y = 0} \cup {(0, 0, 0), (1, 1, 0)}$ 。

理性函数 $R (Φ^{'}, x, y) = R_{1} (Φ^{'}, x, y) + R_{2} (Φ^{'}, x, y) + R_{3} (Φ^{'}, x, y)$ ，记 $λ = (λ_{1}, 1 - λ_{1})$ ， $z = (z_{1}, z_{2}, z_{3}, z_{4})$ ，有

$R_{1} (Φ^{'}, x, y) = \max_{u_{1} \in X_{1}} \min_{{‖ λ ‖}_{1} = 1, λ \in ℜ_{+}^{2}} 〈 λ, G_{1} (u_{1}, x_{2}, y) - G_{1} (x_{1}, x_{2}, y) 〉$

$= \max_{u_{1} \in X_{1}} \min_{{‖ λ ‖}_{1} = 1, λ \in ℜ_{+}^{2}} u_{x_{1}}^{T} [λ_{1} A_{1} + (1 - λ_{1}) A_{2}] t$ ，其中 $u_{x_{1}}^{T} = (u_{1} - x_{1}, x_{1} - u_{1})$ ；

$R_{2} (Φ^{'}, x, y) = \max_{u_{2} \in X_{2}} \min_{{‖ λ ‖}_{1} = 1, λ \in ℜ_{+}^{2}} 〈 λ, G_{2} (x_{1}, u_{2}, y) - G_{2} (x_{1}, x_{2}, y) 〉$

$= \max_{u_{2} \in X_{2}} \min_{{‖ λ ‖}_{1} = 1, λ \in ℜ_{+}^{2}} u_{x_{2}}^{T} [λ_{1} A_{1} + (1 - λ_{1}) A_{2}] x$ ，其中 $u_{x_{2}}^{T} = (u_{2} - x_{2}, x_{2} - u_{2})$ ；

$R_{3} (Φ^{'}, x, y) = \max_{v \in Y} \min_{{‖ z ‖}_{1} = 1, z \in ℜ_{+}^{4}} 〈 z, G (x, y) - G (x, v) 〉$

$= \max_{v \in Y} \min_{{‖ z ‖}_{1} = 1, z \in ℜ_{+}^{4}} [(1 + z_{2} + z_{3}) (y - v)]$ 。

令

$A_{1} = (\begin{matrix} 1 & 0 \\ 0 & 2 \end{matrix})$ ， $A_{2} = (\begin{matrix} 2 & 0 \\ 0 & 1 \end{matrix})$ ，

得博弈 $Φ^{'}$ 的弱Pareto-NS平衡集为

$E (Φ^{'}) = {(x^{*}, y^{*})} = {(x_{1}, x_{2}, y) \in X_{1} \times X_{2} \times Y | \frac{1}{3} \leq x_{1}, x_{2} \leq \frac{2}{3}, y = 0} \cup {(0, 0, 0), (1, 1, 0)}$ 。

因 $R_{1} (Φ^{'}, x, y) = \max_{u_{1} \in X_{1}} \min_{{‖ λ ‖}_{1} = 1, λ \in ℜ_{+}^{2}} (u_{1} - x_{1}) (3 x_{2} - 1 - λ_{1})$ ，有

1) 当 $u_{1} \geq x_{1}$ 时， $λ_{1} = 1$ 使 $(u_{1} - x_{1}) (3 x_{2} - 1 - λ_{1})$ 取最小，得 $(u_{1} - x_{1}) (3 x_{2} - 2)$ ；

2) 当 $u_{1} \leq x_{1}$ 时， $λ_{1} = 0$ 使 $(u_{1} - x_{1}) (3 x_{2} - 1 - λ_{1})$ 取最小，得 $(u_{1} - x_{1}) (3 x_{2} - 1)$ 。

对1)式，当 $x_{2} > \frac{2}{3}$ 时， $u_{1} = 1$ 使 $(u_{1} - x_{1}) (3 x_{2} - 2)$ 取最大，得 $R_{1} (Φ^{'}, x, y) = (1 - x_{1}) (3 x_{2} - 2)$ ；当 $x_{2} \leq \frac{2}{3}$ 时， $u_{1} = x_{1}$ 使 $(u_{1} - x_{1}) (3 x_{2} - 2)$ 取最大，得 $R_{1} (Φ^{'}, x, y) = 0$ ；

对2)式，当 $x_{2} \geq \frac{1}{3}$ 时， $u_{1} = x_{1}$ 使 $(u_{1} - x_{1}) (3 x_{2} - 1)$ 取最大，得 $R_{1} (Φ^{'}, x, y) = 0$ ；当 $x_{2} < \frac{1}{3}$ 时， $u_{1} = 0$ 使 $(u_{1} - x_{1}) (3 x_{2} - 1)$ 取最大，得 $R_{1} (Φ^{'}, x, y) = - x_{1} (3 x_{2} - 1)$ 。

从而，得

$R_{1} (Φ^{'}, x, y) = {\begin{array}{l} - x_{1} (3 x_{2} - 1), & 0 \leq x_{2} < \frac{1}{3}, \\ 0, & \frac{1}{3} \leq x_{2} \leq \frac{2}{3}, \\ (1 - x_{1}) (3 x_{2} - 2), & \frac{2}{3} < x_{2} \leq 1 。 \end{array}$ (4.1)

又 $R_{2} (Φ^{'}, x, y) = \max_{u_{2} \in X_{2}} \min_{{‖ λ ‖}_{1} = 1, λ \in ℜ_{+}^{2}} (u_{2} - x_{2}) (3 x_{1} - 1 - λ_{1})$ ，由对称性得，

$R_{2} (Φ^{'}, x, y) = {\begin{array}{l} - x_{2} (3 x_{1} - 1), & 0 \leq x_{1} < \frac{1}{3}, \\ 0, & \frac{1}{3} \leq x_{1} \leq \frac{2}{3}, \\ (1 - x_{2}) (3 x_{1} - 2), & \frac{2}{3} < x_{1} \leq 1 。 \end{array}$ (4.2)

又 $R_{3} (Φ^{'}, x, y) = \max_{v \in Y} \min_{{‖ z ‖}_{1} = 1, z \in ℜ_{+}^{4}} [(1 + z_{2} + z_{3}) (y - v)]$ ，有

3) 当 $y \geq v$ 时， $z_{2} = z_{3} = 0$ 使 $(1 + z_{2} + z_{3}) (y - v)$ 取最小，得 $y - v$ ；

4) 当 $y < v$ 时， $z_{2} + z_{3} = 1$ 使 $(1 + z_{2} + z_{3}) (y - v)$ 取最小，得 $2 (y - v)$ 。

对3)式， $v = 0$ 使 $y - v$ 取最大，得 $R_{3} (Φ^{'}, x, y) = y$ ， $0 \leq y \leq 1$ ；对4)式， $v = 1$ 使 $2 (y - v)$ 取最大，得 $R_{3} (Φ^{'}, x, y) = 2 (y - 1)$ ，而当 $0 \leq y < 1$ 时， $2 (y - 1)$ 恒小于0，故舍去。

从而，得

$R_{3} (Φ^{'}, x, y) = y$ ， $0 \leq y \leq 1$ 。 (4.3)

综上，由(4.1)，(4.2)，(4.3)式可得理性函数为

$R (Φ^{'}, x, y) = {\begin{array}{l} - x_{1} (3 x_{2} - 1) - x_{2} (3 x_{1} - 1) + y, & 0 \leq x_{1} < \frac{1}{3}, 0 \leq x_{2} < \frac{1}{3}, 0 \leq y \leq 1, \\ - x_{2} (3 x_{1} - 1) + y, & 0 \leq x_{1} < \frac{1}{3}, \frac{1}{3} \leq x_{2} \leq \frac{2}{3}, 0 \leq y \leq 1, \\ (1 - x_{1}) (3 x_{2} - 2) - x_{2} (3 x_{1} - 1) + y, & 0 \leq x_{1} < \frac{1}{3}, \frac{2}{3} < x_{2} \leq 1, 0 \leq y \leq 1, \\ - x_{1} (3 x_{2} - 1) + y, & \frac{1}{3} \leq x_{1} \leq \frac{2}{3}, 0 \leq x_{2} < \frac{1}{3}, 0 \leq y \leq 1, \\ y, & \frac{1}{3} \leq x_{1} \leq \frac{2}{3}, \frac{1}{3} \leq x_{2} \leq \frac{2}{3}, 0 \leq y \leq 1, \\ (1 - x_{1}) (3 x_{2} - 2) + y, & \frac{1}{3} \leq x_{1} \leq \frac{2}{3}, \frac{2}{3} < x_{2} \leq 1, 0 \leq y \leq 1, \\ - x_{1} (3 x_{2} - 1) + (1 - x_{2}) (3 x_{1} - 2) + y, & \frac{2}{3} < x_{1} \leq 1, 0 \leq x_{2} < \frac{1}{3}, 0 \leq y \leq 1, \\ (1 - x_{2}) (3 x_{1} - 2) + y, & \frac{2}{3} < x_{1} \leq 1, \frac{1}{3} \leq x_{2} \leq \frac{2}{3}, 0 \leq y \leq 1, \\ (1 - x_{1}) (3 x_{2} - 2) + (1 - x_{2}) (3 x_{1} - 2) + y, & \frac{2}{3} < x_{1} \leq 1, \frac{2}{3} < x_{2} \leq 1, 0 \leq y \leq 1 。 \end{array}$

接下来考虑对博弈 $Φ^{'}$ 的期望支付函数进行扰动，令

$G_{1}^{m} (x_{1}, x_{2}, y) = [x^{T} A_{1}^{m} t + (1 + \frac{1}{m}) y, x^{T} A_{2}^{m} t + 2 (1 + \frac{1}{m}) y]$ ，

$G_{2}^{m} (x_{1}, x_{2}, y) = [t^{T} A_{1}^{m} x + 2 (1 + \frac{1}{m}) y, t^{T} A_{2}^{m} x + (1 + \frac{1}{m}) y]$ ，

其中，

$A_{1}^{m} = (\begin{matrix} 1 + \frac{1}{m} & 0 \\ 0 & 2 - \frac{1}{m} \end{matrix})$ ， $A_{2}^{m} = (\begin{matrix} 2 + \frac{1}{m} & 0 \\ 0 & 1 - \frac{1}{m} \end{matrix})$ 。

记期望支付函数发生扰动后的博弈为 ${Φ^{'}}^{m}$ ，设 $(x^{* m}, y^{* m})$ 为博弈 ${Φ^{'}}^{m}$ 的弱Pareto-NS平衡，那么

$G_{1}^{m} (x_{1}, x_{2}^{* m}, y^{* m}) - G_{1}^{m} (x_{1}^{* m}, x_{2}^{* m}, y^{* m}) = [(x^{T} - x^{* m T}) A_{1}^{m} t^{* m}, (x^{T} - x^{* m T}) A_{2}^{m} t^{* m}] \notin i n t ℜ_{+}^{2}, \forall x_{1} \in X_{1}$ ；

$G_{2}^{m} (x_{1}^{* m}, x_{2}, y^{* m}) - G_{2}^{m} (x_{1}^{* m}, x_{2}^{* m}, y^{* m}) = [(t^{T} - t^{* m T}) A_{1}^{m} x^{* m}, (t^{T} - t^{* m T}) A_{2}^{m} x^{* m}] \notin i n t ℜ_{+}^{2}, \forall x_{2} \in X_{2}$ ；

$\begin{array}{l} G^{m} (x^{* m}, y^{* m}) - G^{m} (x^{* m}, y) \\ = [(1 + \frac{1}{m}) y^{* m} - (1 + \frac{1}{m}) y, 2 (1 + \frac{1}{m}) y^{* m} - 2 (1 + \frac{1}{m}) y, \\ 2 (1 + \frac{1}{m}) y^{* m} - 2 (1 + \frac{1}{m}) y, (1 + \frac{1}{m}) y^{* m} - (1 + \frac{1}{m}) y] \\ \notin i n t ℜ_{+}^{4}, \forall y \in Y ； \end{array}$

解得

$\frac{1}{3} (1 - \frac{1}{m}) \leq x_{1}^{* m}, x_{2}^{* m} \leq \frac{1}{3} (2 - \frac{1}{m}), y^{* m} = 0$ 。

可得博弈 ${Φ^{'}}^{m}$ 的弱Pareto-NS平衡集为

$E ({Φ^{'}}^{m}) = {(x^{* m}, y^{* m})} = {(x, y) \in X \times Y | \frac{1}{3} (1 - \frac{1}{m}) \leq x_{1}, x_{2} \leq \frac{1}{3} (2 - \frac{1}{m}), y = 0} \cup {(0, 0, 0), (1, 1, 0)}$ 。

扰动后理性函数 $R ({Φ^{'}}^{m}, x, y) = R_{1} ({Φ^{'}}^{m}, x, y) + R_{2} ({Φ^{'}}^{m}, x, y) + R_{3} ({Φ^{'}}^{m}, x, y)$ ，其中

$R_{1} ({Φ^{'}}^{m}, x, y) = \max_{u_{1} \in X_{1}} \min_{{‖ λ ‖}_{1} = 1, λ \in ℜ_{+}^{2}} (u_{1} - x_{1}) (3 x_{2} - 1 - λ_{1} + \frac{1}{m})$ ；

$R_{2} ({Φ^{'}}^{m}, x, y) = \max_{u_{2} \in X_{2}} \min_{{‖ λ ‖}_{1} = 1, λ \in ℜ_{+}^{2}} (u_{2} - x_{2}) (3 x_{1} - 1 - λ_{1} + \frac{1}{m})$ ；

$R_{3} ({Φ^{'}}^{m}, x, y) = \max_{v \in Y} \min_{{‖ z ‖}_{1} = 1, z \in ℜ_{+}^{4}} [(1 + z_{2} + z_{3}) ((1 + \frac{1}{m}) y - (1 + \frac{1}{m}) v)]$ 。

同理可得，

$R_{1} ({Φ^{'}}^{m}, x, y) = {\begin{array}{l} - x_{1} (3 x_{2} - 1 + \frac{1}{m}), & 0 \leq x_{2} < \frac{1}{3} (1 - \frac{1}{m}), \\ 0, & \frac{1}{3} (1 - \frac{1}{m}) \leq x_{2} \leq \frac{1}{3} (2 - \frac{1}{m}), \\ (1 - x_{1}) (3 x_{2} - 2 + \frac{1}{m}), & \frac{1}{3} (2 - \frac{1}{m}) < x_{2} \leq 1 。 \end{array}$ (4.4)

$R_{2} ({Φ^{'}}^{m}, x, y) = {\begin{array}{l} - x_{2} (3 x_{1} - 1 + \frac{1}{m}), & 0 \leq x_{1} < \frac{1}{3} (1 - \frac{1}{m}), \\ 0, & \frac{1}{3} (1 - \frac{1}{m}) \leq x_{1} \leq \frac{1}{3} (2 - \frac{1}{m}), \\ (1 - x_{2}) (3 x_{1} - 2 + \frac{1}{m}), & \frac{1}{3} (2 - \frac{1}{m}) < x_{1} \leq 1 。 \end{array}$ (4.5)

$R_{3} ({Φ^{'}}^{m}, x, y) = (1 + \frac{1}{m}) y$ ， $0 \leq y \leq 1$ 。 (4.6)

进而有，

$\begin{array}{l} R ({Φ^{'}}^{m}, x, y) \\ = {\begin{array}{l} - x_{1} (3 x_{2} - 1 + \frac{1}{m}) - x_{2} (3 x_{1} - 1 + \frac{1}{m}) + (1 + \frac{1}{m}) y, & 0 \leq x_{1} < \frac{1}{3} (1 - \frac{1}{m}), 0 \leq x_{2} < \frac{1}{3} (1 - \frac{1}{m}), 0 \leq y \leq 1, \\ - x_{2} (3 x_{1} - 1 + \frac{1}{m}) + (1 + \frac{1}{m}) y, & 0 \leq x_{1} < \frac{1}{3} (1 - \frac{1}{m}), \frac{1}{3} (1 - \frac{1}{m}) \leq x_{2} \leq \frac{1}{3} (2 - \frac{1}{m}), 0 \leq y \leq 1, \\ (1 - x_{1}) (3 x_{2} - 2 + \frac{1}{m}) - x_{2} (3 x_{1} - 1 + \frac{1}{m}) + (1 + \frac{1}{m}) y, & 0 \leq x_{1} < \frac{1}{3} (1 - \frac{1}{m}), \frac{1}{3} (2 - \frac{1}{m}) < x_{2} \leq 1, 0 \leq y \leq 1, \\ - x_{1} (3 x_{2} - 1 + \frac{1}{m}) + (1 + \frac{1}{m}) y, & \frac{1}{3} (1 - \frac{1}{m}) \leq x_{1} \leq \frac{1}{3} (2 - \frac{1}{m}), 0 \leq x_{2} < \frac{1}{3} (1 - \frac{1}{m}), 0 \leq y \leq 1, \\ (1 + \frac{1}{m}) y, & \frac{1}{3} (1 - \frac{1}{m}) \leq x_{1} \leq \frac{1}{3} (2 - \frac{1}{m}), \frac{1}{3} (1 - \frac{1}{m}) \leq x_{2} \leq \frac{1}{3} (2 - \frac{1}{m}), 0 \leq y \leq 1, \\ (1 - x_{1}) (3 x_{2} - 2 + \frac{1}{m}) + (1 + \frac{1}{m}) y, & \frac{1}{3} (1 - \frac{1}{m}) \leq x_{1} \leq \frac{1}{3} (2 - \frac{1}{m}), \frac{1}{3} (2 - \frac{1}{m}) < x_{2} \leq 1, 0 \leq y \leq 1, \\ - x_{1} (3 x_{2} - 1 + \frac{1}{m}) + (1 - x_{2}) (3 x_{1} - 2 + \frac{1}{m}) + (1 + \frac{1}{m}) y, & \frac{1}{3} (2 - \frac{1}{m}) < x_{1} \leq 1, 0 \leq x_{2} < \frac{1}{3} (1 - \frac{1}{m}), 0 \leq y \leq 1, \\ (1 - x_{2}) (3 x_{1} - 2 + \frac{1}{m}) + (1 + \frac{1}{m}) y, & \frac{1}{3} (2 - \frac{1}{m}) < x_{1} \leq 1, \frac{1}{3} (1 - \frac{1}{m}) \leq x_{2} \leq \frac{1}{3} (2 - \frac{1}{m}), 0 \leq y \leq 1, \\ (1 - x_{1}) (3 x_{2} - 2 + \frac{1}{m}) + (1 - x_{2}) (3 x_{1} - 2 + \frac{1}{m}) + (1 + \frac{1}{m}) y, & \frac{1}{3} (2 - \frac{1}{m}) < x_{1} \leq 1, \frac{1}{3} (2 - \frac{1}{m}) < x_{2} \leq 1, 0 \leq y \leq 1 。 \end{array} \end{array}$

接下来我们通过理性函数图对上述例子进行直观说明，记 $x^{'} = x_{1} = x_{2}$ 。

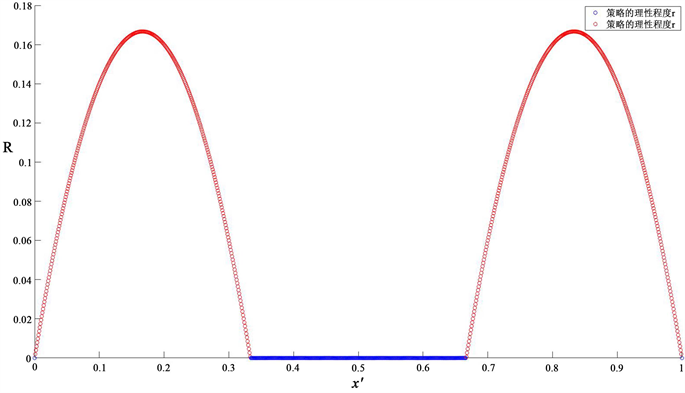
Figure 1. $y = 0$ and players 1 and 2 choose the same strategy $x^{'}$

图1. $y = 0$ 且局中人1和2选择相同的策略 $x^{'}$

图1表明，若局中人1和2选择相同的策略，即 $(x, y) \in {(x_{1}, x_{2}, y) \in X_{1} \times X_{2} \times Y | \frac{1}{3} \leq x_{1} = x_{2} \leq \frac{2}{3}, y = 0}$ 时，有 $R (Φ^{'}, x, y) = 0$ ，对应于完全理性。

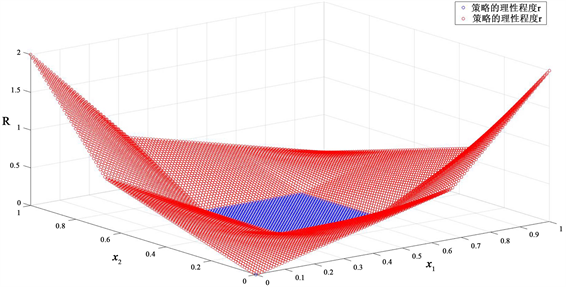
Figure 2. $y = 0$ and players 1 and 2 choose all strategies

图2. $y = 0$ 且局中人1和2选择所有策略

图2表明，若 $(x, y) \in E (Φ^{'})$ ，则 $R (Φ^{'}, x, y) = 0$ ，对应于完全理性；若 $R (Φ^{'}, x, y) = 0$ ，则 $(x, y) \in E (Φ^{'})$ 。当 $(x, y) \notin E (Φ^{'})$ 时， $R (Φ^{'}, x, y) > 0$ ，对应于有限理性，且越偏离平衡集对应的理性函数值越大，表明局中人的理性程度越低，且当 $(x, y) \in {(0, 1, 0), (1, 0, 0)}$ 时， $R (Φ^{'}, x, y) = 2$ 达到最大值，此时局中人的理性程度是最低的。其中图1只是图2的一部分。

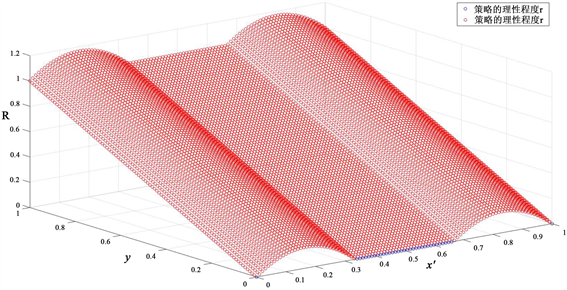
Figure 3. $y \in [0, 1]$ and players 1 and 2 choose the same strategy $x^{'}$

图3. $y \in [0, 1]$ 且局中人1和2选择相同的策略 $x^{'}$

图3表明，当 $(x, y) \in E (Φ^{'})$ 时， $R (Φ^{'}, x, y) = 0$ ，此时局中人是完全理性的；当 $(x, y) \notin E (Φ^{'})$ 时， $R (Φ^{'}, x, y) > 0$ ，且选取的 $(x, y)$ 越偏离平衡集 $E (Φ^{'})$ ， $R (Φ^{'}, x, y)$ 越大。当 $y \neq 0$ 时，随着y值增大，对应的理性函数值 $R (Φ^{'}, x, y)$ 逐渐增大，体现了不确定参数对局中人理性程度的影响，即表明局中人对不确定参数的态度是悲观的和保守的。

当对期望支付函数进行扰动时，我们进一步观察扰动参数 $\frac{1}{m}$ 对理性函数值的影响。为了作图方便，接下来我们只考虑局中人1和2选择相同策略的情形。

Figure 4. $y = 0$ and $\frac{1}{m} \in [0, 0.5]$

图4. $y = 0$ 且 $\frac{1}{m} \in [0, 0.5]$

图4表明，当 $(x, y) \in {(x_{1}, x_{2}, y) \in X_{1} \times X_{2} \times Y | 0 < x_{1} = x_{2} < \frac{1}{3} (1 - \frac{1}{m}), y = 0}$ 时，扰动参数 $\frac{1}{m}$ 越大，对应的 $R ({Φ^{'}}^{m}, x, y)$ 越小，说明局中人的理性程度越来越高；当 $(x, y) \in E ({Φ^{'}}^{m})$ 时，无论扰动参数 $\frac{1}{m}$ 如何变化， $R ({Φ^{'}}^{m}, x, y) = 0$ ，说明局中人处于完全理性状态；当 $(x, y) \in {(x_{1}, x_{2}, y) \in X_{1} \times X_{2} \times Y | \frac{1}{3} (2 - \frac{1}{m}) < x_{1} =$ $x_{2} < 1, y = 0}$ 时，扰动参数 $\frac{1}{m}$ 越大，对应的 $R ({Φ^{'}}^{m}, x, y)$ 越大，说明局中人的理性程度越来越低。即若 $(x, y) \in E ({Φ^{'}}^{m})$ ，则 $R ({Φ^{'}}^{m}, x, y) = 0$ ；若 $R ({Φ^{'}}^{m}, x, y) = 0$ ，则 $(x, y) \in E ({Φ^{'}}^{m})$ 。当 $\frac{1}{m} = 0$ 时，图4与图1一致。

Figure 5. $y \in [0, 1]$ and $\frac{1}{m} = 0.50$

图5. $y \in [0, 1]$ 且 $\frac{1}{m} = 0.50$

Figure 6. $y \in [0, 1]$ and $\frac{1}{m} = 0.10$

图6. $y \in [0, 1]$ 且 $\frac{1}{m} = 0.10$

Figure 7. $y \in [0, 1]$ and $\frac{1}{m} = 0.01$

图7. $y \in [0, 1]$ 且 $\frac{1}{m} = 0.01$

图5~7表明，当 $(x, y) \in E ({Φ^{'}}^{m})$ 时，有 $R ({Φ^{'}}^{m}, x, y) = 0$ ；当 $(x, y) \notin E ({Φ^{'}}^{m})$ 时，扰动参数 $\frac{1}{m}$ 越大，对应的理性函数值 $R ({Φ^{'}}^{m}, x, y)$ 越大；反之，随着扰动参数 $\frac{1}{m}$ 逐渐减小， $\frac{1}{m}$ 对局中人的理性程度扰动也越来越小；当 $\frac{1}{m} \to 0$ 时，有 ${Φ^{'}}^{m} \to Φ^{'}$ ，此时局中人的理性程度非常高，趋近于完全理性。

显然，该算例满足引理3.1~3.3，进而满足引理2.1的所有条件，故定理3.1成立。即当博弈 $Φ^{'} \in Λ$ 的期望支付函数 $G = (G_{1}, G_{2})$ 发生扰动时，有限理性模型 $ϒ$ 在 $Φ^{'}$ 是结构稳定的，且对弱 $ε$ -Pareto-NS平衡是鲁棒的。进而，有限理性下该不确定参数多目标博弈 $Φ^{'}$ 的弱Pareto-NS平衡是稳定的。

5. 总结

本文建立了不确定参数下多目标博弈的有限理性模型，并基于弱Pareto-NS平衡的定义构造理性函数，得到了该有限理性模型的稳定性结论。进一步，我们通过算例4.1对不确定参数下多目标博弈平衡的稳定性进行了直观的刻画和分析。

基金项目

本文获得贵州省科技计划项目(黔科合基础-ZK[2022]一般168)；国家自然科学基金项目(No. 11271098)；贵州大学引进人才科研项目(No. [2017]59)。

文章引用

陈聪利,汤卫,王春. 有限理性下不确定参数多目标博弈平衡的稳定性
Stability of Equilibria for Multiobjective Games with Uncertain Parameters under Bounded Rationality[J]. 运筹与模糊学, 2023, 13(02): 1242-1257. https://doi.org/10.12677/ORF.2023.132127

参考文献

1. Simon, H.A. 管理行为[M]. 杨硕, 等, 译. 北京: 北京经济学院出版社, 1991.

2. Anderlini, L. and Canning, D. (2001) Structural Stability Implies Robustness to Bounded Rationality. Journal of Economic Theory, 101, 395-422. https://doi.org/10.1006/jeth.2000.2784

3. Yu, C. and Yu, J. (2006) On Structural Stability and Robustness to Bounded Rationality. Nonlinear Analysis, 65, 583-592. https://doi.org/10.1016/j.na.2005.09.039

4. Yu, C. and Yu, J. (2007) Bounded Rationality in Multiobjective Games. Nonlinear Analysis, 67, 930-937. https://doi.org/10.1016/j.na.2006.06.050

5. 俞建. 博弈论与非线性分析[M]. 北京: 科学出版社, 2008.

6. 俞建. 有限理性与博弈论中平衡点集的稳定性[M]. 北京: 科学出版社, 2017.

7. 俞建. 几类考虑有限理性平衡问题解的稳定性[J]. 系统科学与数学, 2009, 29(7): 999-1008.

8. 俞建, 贾文生. 有限理性研究的博弈论模型[J]. 中国科学: 数学, 2020, 50(9): 1375-1386.

9. 王红蕾, 俞建. 有限理性与多目标问题解的稳定性[J]. 运筹学学报, 2008, 12(1): 104-108.

10. 王红蕾, 俞建. 有限理性与多目标最优化问题弱有效解集的稳定性[J]. 中国管理科学, 2008, 16(4): 155-158.

11. Zhukovskii, V.I. (1994) Linear Quadratic Differential Games. Naoukova Doumka, Kiev.

12. 杨哲, 蒲勇健. 广义不确定下广义多目标博弈弱Pareto-Nash均衡点集的存在性与本质连通区[J]. 系统科学与数学, 2011, 31(12): 1613-1621.

13. 杨哲, 蒲勇健. 不确定性下多主从博弈中均衡的存在性[J]. 控制与决策, 2012, 27(5): 736-740.

14. 杨哲, 蒲勇健, 郭心毅. 不确定性下多目标博弈中弱Pareto-NS均衡的存在性[J]. 系统工程理论与实践, 2013, 33(3): 660-665.

15. 赵薇, 杨辉, 吴隽永. 不确定参数下群体博弈均衡的存在性与通有稳定性[J]. 应用数学学报, 2020, 43(4): 627-638.

16. 陆辰超, 邬冬华. 不确定性下非合作博弈的有限理性模型及良定性[J]. 应用数学与计算数学学报, 2016, 30(3): 339-348.

17. 王能发. 有限理性下不确定性博弈均衡的稳定性[J]. 应用数学学报, 2017, 40(4): 562-572.

18. Zhao, W., Yang, H., Deng, X.C. and Zhong, C.Y. (2021) Stability of Equilibria for Population Games with Uncertain Parameters under Bounded Rationality. Journal of Inequalities and Applications, 2021, Article No. 15. https://doi.org/10.1186/s13660-020-02544-0

NOTES

^*通讯作者。

期刊菜单