Advances in Education
Vol.06 No.05(2016), Article ID:18676,6
pages
10.12677/AE.2016.65035
Concise Remarks on Transfer Matrix of Applied Optics
Long Jin
School of Science,

Received: Sep. 11th, 2016; accepted: Sep. 27th, 2016; published: Sep. 30th, 2016
Copyright © 2016 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
In applied optics teaching, matrix analysis method possesses the characteristic of clear, simple physical model and need not deliberately stress the symbols relationship of the object plane and image plane. For large optical path and the paraxial imaging system calculation, using this method can get twice the result with the half effort. In this paper, we use traditional light path calculation and matrix optics method to calculate the spherical optical system of image plane position and image plane size, making a brief explanation to the imaging regulation, and expound the advantage of matrix optics and the aspects for attention.
Keywords:Teaching Reform, Applied Optics, Transfer Matrix

浅析应用光学中的传递矩阵
靳龙
湖北汽车工业学院理学院,湖北 十堰

收稿日期:2016年9月11日;录用日期:2016年9月27日;发布日期:2016年9月30日

摘 要
在应用光学教学中,矩阵分析方法具有思路清晰,物理模型简单,不用刻意强调物、像面的符号关系,对于大型光路系统的近轴成像计算,采用此方法可起到事半功倍的效果。本文分别利用传统光路计算和矩阵光学分析方法计算了球面光学系统的像面位置和像面大小,对其成像规律作了简要说明,并结合教学实践,阐述了光学矩阵分析的优点和应该注意的方面。
关键词 :教学改革,应用光学,传递矩阵

1. 引言
应用光学是光电信息科学与工程,测控技术与仪器等专业的主干专业基础课,也是这些专业学生接触到的第一门工程类课程。本课程以几何光学原理、概念为基础,全面地研究了光线在典型和现代光学仪器中的传输规律 [1] 。在本科教学过程中,傍轴近似和理想光学系统成像规律是应用光学的教学重点,这些理论以线性光学基本定理为指导,忽略了像差和色差的影响,是光学设计中的初级计算方法。研究它们成像规律的意义在于既可当作实际光学系统成像质量的标准,又可作为实际光学系统成像计算的初始值 [2] 。
矩阵论是数学的一个分支,它的研究对象是向量,向量空间(或称线性空间),线性变换和有限维的线性方程组,向量空间是现代数学的一个重要课题 [3] 。在傍轴近似中,光线是限定在子午面内,其量值用离轴角度和离轴距离来表征。当光线在光学系统中传输时,实际经历了平移和折射(反射)变换,这些变换都是向量空间中的线性变换,因而物空间和像空间的光线量值可以通过一系列的变换矩阵进行描述 [4] 。另外近年来,在激光光学中,也广泛使用传递矩阵描述高斯光束的传输规律和物面、像面变换特征 [5] 。因此,探索应用光学中传递矩阵的教学改革,对于经典光学和量子光电教学,都有重要的意义。
2. 基本理论
设光线在物、像横截面上的参数分别为h,u和h',u'。其中,h和h'为物,像离轴距离,u和u'为其离轴角度。在傍轴区域光线可以成完善的像,其函数关系为 [6]
 (1)
(1)
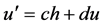 (2)
(2)
此时光线矢量的线性变换可以用矩阵表示为
 (3)
(3)
令
 ,
, (4)
(4)
 (5)
(5)
则光线矢量的线性变换为
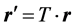 (6)
(6)
其中,一些光学元件的传递矩阵T可由几何光学方法导出。接下来,我们首先推导光波在均匀介质中的传递矩阵,并阐明其教学要点。然后,列举一些几何光学元件的传递矩阵,以供后续章节使用。
2.1. 均匀介质的传递矩阵
根据几何光学费马原理,光在均匀介质中沿直线传输,其传播规律如图1所示。
此时参数h,u和 ,
,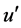 为两共轭面间的光线垂轴线量和夹角,其符号规定与传统光路计算中的新笛卡尔法则一致。则光线夹角之间的关系为:
为两共轭面间的光线垂轴线量和夹角,其符号规定与传统光路计算中的新笛卡尔法则一致。则光线夹角之间的关系为:
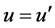 (7)
(7)
光线垂轴线量之间的关系为:
 (8)
(8)
对于傍轴近似,则
 (9)
(9)
结合光线矢量的线性变换式(6),可得均匀介质的传递矩阵为:
 (10)
(10)
从以上传递矩阵推导过程可以看出,其所使用的符号法则和近似条件都与传统光学的计算范畴一致,并且在其推导中所使用的几何原理正是传统几何光学的演绎方法。因而,对传递矩阵的推导,不仅是对原有几何光学理论的温习,而且使学生掌握了解决光线变换问题的新方法。
2.2. 折射球面的传递矩阵
 (11)
(11)
其中,r为球面曲率半径,n和 分别为入射介质和出射介质折射率。由于反射定律可以看作折射定律的特殊形式,因此,令
分别为入射介质和出射介质折射率。由于反射定律可以看作折射定律的特殊形式,因此,令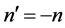 ,可得反射球面镜的传递矩阵为
,可得反射球面镜的传递矩阵为
 (12)
(12)
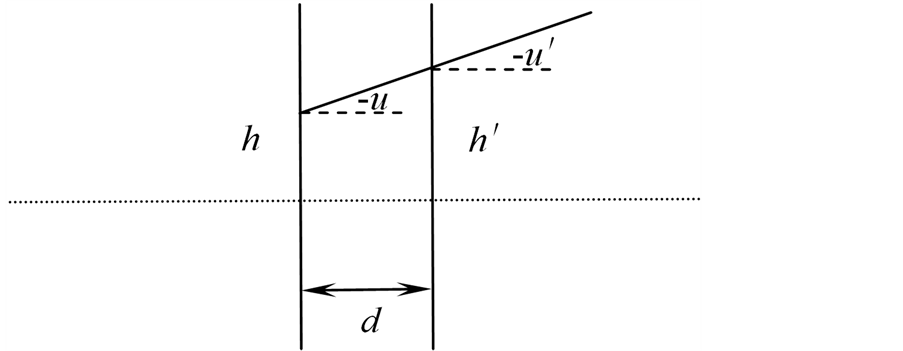
Figure 1. The principle diagram of the light wave propagation in homogeneous medium
图1. 光波在均匀介质中传播原理图
当光学系统由N个光学元件构成,可以看作光线依次通过包括均匀介质在内的基本光学单元,其入射光线矢量和出射光线矢量关系为:
 (13)
(13)
2.3. 光学系统共轭面间的传递矩阵
光学系统的物空间和相空间是一对共轭面,其传递矩阵可以看作光线依次通过上述基本光学单元,大小为
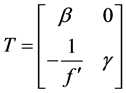 (14)
(14)
其中,β为垂直放大率,γ为角放大率, 为光学系统的像方焦距。
为光学系统的像方焦距。
3. 传统光路计算和矩阵光学方法对比
假设有一凹面反射镜和一凸面反射镜,其曲率半径均为10 cm,现将它们面对面的放置在相距20 cm的同一轴线上,其中,凹面反射镜在左,凸面反射镜在右,并在它们顶点中心放置一高3 cm的物体,求物体先经过凸面反射镜再经过凹面反射镜所成的像面位置和大小。
3.1. 传统方法
根据光学新笛卡尔法则和球面反射镜的成像公式 [2]
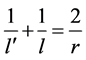 (15)
(15)
其中 ,可知首次成像后的
,可知首次成像后的 在凸面镜顶点的右侧10/3 cm处,放大倍率为
在凸面镜顶点的右侧10/3 cm处,放大倍率为 。
。
当光波二次成像于凹面镜时,其物面距凹面镜顶点大小为 ,再次根据成像公式(15)可求得像面距凹面镜顶点大小为
,再次根据成像公式(15)可求得像面距凹面镜顶点大小为 ,放大倍率为
,放大倍率为 ,因此像的总放大倍率为
,因此像的总放大倍率为
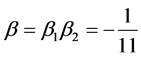 (16)
(16)
3.2. 矩阵方法
设像面相对凹面反射镜的相距为 ,则从物面到像面的传递矩阵为
,则从物面到像面的传递矩阵为
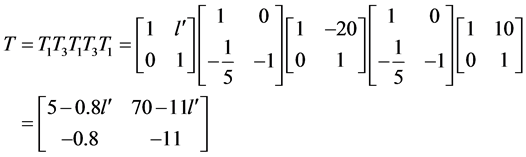 (17)
(17)
对比光学系统共轭面间的传递矩阵(14)可得
 ,
, (18)
(18)
因此,同样可得 ,
, 。表示像面位于凹面反射镜右方70/11 cm处,成倒立的像,其大小为3/11 cm。
。表示像面位于凹面反射镜右方70/11 cm处,成倒立的像,其大小为3/11 cm。
从以上对比计算可以看出,采用矩阵分析和传统光学计算方法所得到的结果一致,但传统光学计算方法需要根据物体成像时经过光学元件的先后顺序逐次计算,这对于大型复杂光学系统,显然运算量巨大,并且大大增加了出差的几率。而矩阵方法则只需一次运算,并且二阶矩阵的乘法计算也相对简单。
4. 教学心得体会
目前,几何光学教学以传统光线追迹方法为主,此方法对于单光学元件的成像分析不仅物理概念清晰,而且几何图形直观。但对于光学系统组合的成像计算,学生普遍反映计算量大,公式繁琐,有时都不知道怎么几何作图。即使对于最简单的双光组组合,转面公式的符号也容易搞混。在利用正切法和截距法求解相关习题时,学生经常找不到图形的相似关系及对应公式,有时花费了很大的精力,但由于一个几何物(像)点的位置在作图时有偏差而导致前功尽弃。近年来,一些应用光学教材引入了矩阵光学基本理论,其在大型光学系统组合成像分析时,思路清晰,物理模型简单,不用刻意强调物、像面的符号关系,并且计算量远小于传统光学分析方法,学生在求解时很少出现答案错误。作者在教学过程中,屡次采用矩阵光学的教学手段,并且和传统光线追迹方法结合在一起,而不是孤立的把矩阵光学作为一节或一章,这样学生不仅温习了旧的光学理论,并且加深了对各光学元件传递矩阵的理解,例如对于上面均匀介质传递矩阵的分析,学生很容易的就理解了矩阵运算中不用刻意强调物、像面的符号关系的缘由。另外,通过矩阵光学的学习,学生对光学线性变换有了更加深刻的认识,除了解析几何分析外,学生能够从另外一个数学分支看待光学成像问题,这对后续光学设计的教与学,都是有所裨益的。但是,需要强调的是,在矩阵计算中,各光学元件的传递矩阵是按照光线传输时的先后顺序从右向左依次相乘,这和我们的惯性思维正好相反,学生在计算过程中很容易记错,这一点应特别强调。另外,矩阵光学中光学元件都有其对应的传递矩阵,所以在成像计算时,一些几何光线的传输路径不如传统几何光学分析方法直观,因为光线的传输与变换都由相应的二阶矩阵体现,每个矩阵类似于一个“黑匣子”,每个黑匣子依次进行运算后,就得到了最终结果。所以,在教学过程中,如果一味地贪图运算和逻辑简单,把重心放到矩阵光学上而忽视传统光线追迹方法教学,便会适得其反。例如,某学生在应用光学考试中,遇到光学系统组合的计算,却把一个双凹厚透镜的传递矩阵遗忘了,由于他的基本几何光学理论不扎实,既不会从传统光学方法推导出双凹厚透镜传递矩阵,更不可能按照光线追迹依次计算各物、像关系,因而他虽然掌握了矩阵光学理论,也无从下手做题。这些反面教材,我们是应该吸取教训的。矩阵光学只能作为传统几何光学教学模式的有效补充,而不能宣兵夺主,这一点是相关专业、学科老师和学生都要特别注意的地方。
5. 结束语
在应用光学教学中,矩阵分析具有思路清晰,物理模型简单,不用刻意强调物、像面的符号关系,对于大型光路系统的傍轴区成像计算,采用此方法可起到事半功倍的效果。此方法作为传统几何光学教学模式的有效补充,若适宜地采用,不仅可以激发学生学习光学课程的热情,减缓他们大量的计算压力,而且为后续光学设计课程学习提供了重要的分析手段。
基金项目
感谢湖北汽车工业学院理学院光电科学与技术系光电信息科学与工程专业教研室全体成员为本文所做的贡献和湖北汽车工业学院2016年专业建设项目(JX201644)专项支助。
文章引用
靳 龙. 浅析应用光学中的传递矩阵
Concise Remarks on Transfer Matrix of Applied Optics[J]. 教育进展, 2016, 06(05): 235-240. http://dx.doi.org/10.12677/AE.2016.65035
参考文献 (References)
- 1. 郭仁慧, 高志山. 谈应用光学的改进方法[J]. 高教论坛, 2009(1): 90-92.
- 2. 石顺祥, 王学恩. 物理光学与应用光学[M]. 西安: 电子科技大学出版社, 2014: 359-360, 384-387.
- 3. 程云鹏, 张凯院. 矩阵论[M]. 西安: 西北工业大学出版社, 2013: 1-10.
- 4. Ghatak, A. (2008) Optics. Higher Education Press, Beijing, 67-68.
- 5. 周炳琨, 高以智. 激光原理[M]. 北京: 国防工业出版社, 2014: 33-38.
- 6. 张以谟. 应用光学[M]. 北京: 电子工业出版社, 2008: 65-70.