Pure Mathematics
Vol.4 No.05(2014), Article
ID:14115,3
pages
DOI:10.12677/PM.2014.45031
The Nonexistence Results of Radial Solutions to Some Chern-Simons-Schrödinger Equations
Department of Mathematics, School of Mathematics and Computer Science, Jianghan University, Wuhan
Email: wanyouyan@jhun.edu.cn
Copyright © 2014 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received: Jul. 12th, 2014; revised: Aug. 9th, 2014; accepted: Aug. 17th, 2014
ABSTRACT
Using variational methods, we obtain that the nonexistence of radial solutions to some Chern-Simons-Schrödinger equations with radial symmetric potentials and special nonlinearities when the parameter λ is positive.
Keywords:Chern-Simons-Schrödinger Equations, Radial Solutions, The Nonexistence

一类陈–西蒙斯–薛定谔方程
径向对称解的非存在性结论
董奎良,张 灿,张志永,谢 俊,朱康力,万优艳
江汉大学数学与计算机科学学院数学系,武汉
Email: wanyouyan@jhun.edu.cn
收稿日期:2014年7月12日;修回日期:2014年8月9日;录用日期:2014年8月17日

摘 要
通过变分法研究得到:当参数λ大于零时,一类带正的径向对称的位势和特殊非线性项的陈–西蒙斯–薛定谔方程不存在非平凡的径向对称解。
关键词
陈–西蒙斯–薛定谔方程,径向对称解,非存在性

1. 引言
在对高温超导电性、分数量子霍尔效应和Aharovnov-Bohm扩散等负离子量子物理的研究中,我们常常需要研究陈–西蒙斯–薛定谔方程和方程组,参见[1] -[4] 。在文献[5] [6] 中,作者通过拟设和库仑规范条件,将陈–西蒙斯–薛定谔方程转化为下列带非局部项的椭圆型薛定谔方程
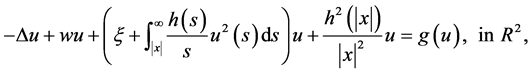 (1)
(1)
其中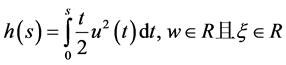 。
。
当非线性项 时,其中
时,其中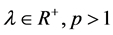 ,文献[5] [6] 中作者用变分法研究得到(1)径向对称基态解的存在性,非存在性和多解的存在性。
,文献[5] [6] 中作者用变分法研究得到(1)径向对称基态解的存在性,非存在性和多解的存在性。
本文我们主要研究下列陈–西蒙斯–薛定谔方程
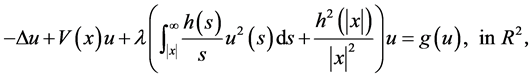 (2)
(2)
其中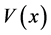
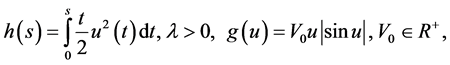 满足下列条件:
满足下列条件:
(V1)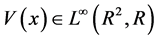 ;
;
(V2)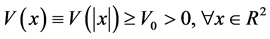 。
。
当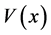 是正的径向对称的位势且(2)右边非线性项g(u)是渐近线性的情形时,文献[7] 中作者证明了方程(2)解和多解的存在性,并且得到当λ充分大时,(2)不存在非平凡的径向对称解。
是正的径向对称的位势且(2)右边非线性项g(u)是渐近线性的情形时,文献[7] 中作者证明了方程(2)解和多解的存在性,并且得到当λ充分大时,(2)不存在非平凡的径向对称解。
定义1:如果u(x)满足方程(2)并且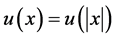 ,则称其为方程(2)的径向对称的解;如果进一步假设
,则称其为方程(2)的径向对称的解;如果进一步假设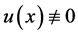 则称其为非平凡的,否则称为平凡的。
则称其为非平凡的,否则称为平凡的。
本文考虑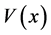 是正的径向对称的位势且非线性项
是正的径向对称的位势且非线性项 这种情形。很明显,此时g(u)在无穷远处不是渐近线性的、不是超线性的,也不是次线性的,但有
这种情形。很明显,此时g(u)在无穷远处不是渐近线性的、不是超线性的,也不是次线性的,但有 。受[7] 和[8] 中方法的启发,本文的主要结论如下。
。受[7] 和[8] 中方法的启发,本文的主要结论如下。
定理1:假设 满足(V1)和(V2)且
满足(V1)和(V2)且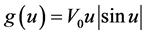 ,那么对所有的
,那么对所有的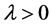 方程(2)没有非平凡的径向对称解。
方程(2)没有非平凡的径向对称解。
2. 预备知识
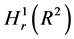 表示径向对称的Sobolev空间,其范数定义为:
表示径向对称的Sobolev空间,其范数定义为:
 .
.
上述范数与下列范数是等价的:
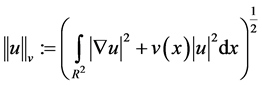 .
.
我们定义能量泛函 ,
,
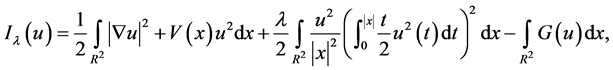
其中 。
。
类似于[7] 中性质2.3,我们可以得到下述引理。
引理1:假设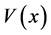 满足(V1)和(V2)且
满足(V1)和(V2)且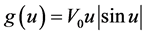 ,则能量泛函
,则能量泛函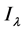 在
在 中是连续可微的并且它的临界点u是(2)的弱解。此外,假设u是
中是连续可微的并且它的临界点u是(2)的弱解。此外,假设u是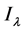 的一个临界点,则
的一个临界点,则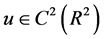 ,即(2)的弱解也是它的经典解。
,即(2)的弱解也是它的经典解。
下面我们来回忆[7] 中一个重要不等式,我们在对主要定理的证明中会用到它。
引理2:如果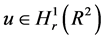 ,那么我们有
,那么我们有
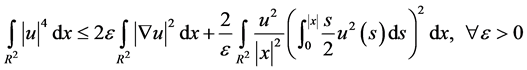 .
.
3. 定理1的证明
假设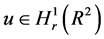 是(2)的一个解。由引理1,可将(2)式两边同时乘以u并且分部积分得:
是(2)的一个解。由引理1,可将(2)式两边同时乘以u并且分部积分得:
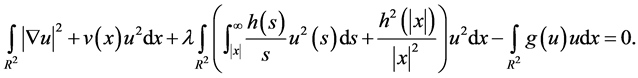
因为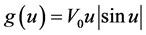 ,所以
,所以
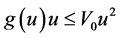 (3)
(3)
由(3)和引理2,选取 ,我们有
,我们有
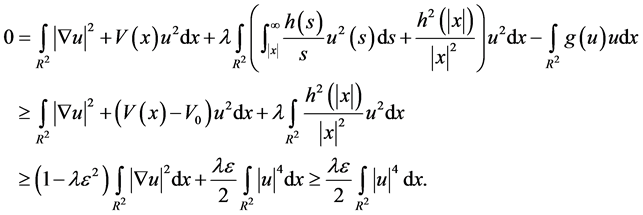
因此,当 时,
时,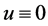 。故当
。故当 时,(2)没有非平凡的径向对称解。
时,(2)没有非平凡的径向对称解。
致 谢
本文受江汉大学2014年度大学生创新训练项目资助,作者在此表示衷心感谢!
基金项目
江汉大学2014年度大学生创新训练项目2014yb189。
参考文献 (References)
- [1] Dunne, G. (1995) Self-dual Chern-Simons theories. Springer.
- [2] Jackiw, R. and Pi, S.-Y. (1990) Classical and quantal non-relativistic Chern-Simons theory. Physical Review D, 42, 3500-3513.
- [3] Jackiw, R. and Pi, S.-Y. (1992) Self-dual Chern-Simons solitons. Progress of Theoretical Physics Supplement, 107, 1-40.
- [4] Liu, B., Smith, P., Tataru, D. (preprint) Local wellposedness of Chern-Simons-Schrödinger.
- [5] Byeon, J., Huh, H. and Seok, J. (2012) Standing waves of nonlinear Schrödinger equations with the gauge field. Journal of Functional Analysis, 263, 1575-1608.
- [6] Huh, H. (2012) Standing waves of the Schrödinger equation coupled with the Chern-Sinons gauge field. Journal of Mathematical Physics, 53, Article ID: 063702.
- [7] Wan, Y. and Tan, J. (2014) Standing waves for the Chern-Simons-Schrödinger systems without (AR) condition. Journal of Mathematical Analysis and Applications, 415, 422-434.
- [8] Wang, Z. and Zhou, H. (2007) Positive solution for a nonlinear stationary Schrödinger-Poisson system in
 . Discrete and Continuous Dynamical Systems, 18, 809-816.
. Discrete and Continuous Dynamical Systems, 18, 809-816.