Pure Mathematics
Vol.06 No.04(2016), Article ID:18184,23
pages
10.12677/PM.2016.64052
Continuous Bounded Positive Solutions of Black-Scholes Equations with Multiple Singular Inner Boundary
Xiaoqing Wu
College of Science, Southwest Petroleum University, Chengdu Sichuan
Email: wuxiaoqing_swpu@163.com
Received: Jul. 12th, 2016; accepted: Aug. 6th, 2016; published: Aug. 9th, 2016
Copyright © 2016 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
In this paper, the mathematical model is established of the Black Scholes equation in the region 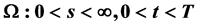 with a number of singular inner boundary
with a number of singular inner boundary ,
, 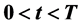 ,
, 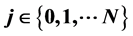 , and introduce the generalized characteristic function method to be able to obtain the exact solution of the mathematical model, and further to obtain singular boundary is exponential function curve
, and introduce the generalized characteristic function method to be able to obtain the exact solution of the mathematical model, and further to obtain singular boundary is exponential function curve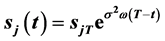 ,
,  It is proved that the maximum value of the exact solution
It is proved that the maximum value of the exact solution  in the closed interval
in the closed interval 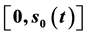 is on the singular boundary
is on the singular boundary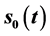 , the maximum value in the interval
, the maximum value in the interval 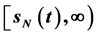 is obtained on the singular boundary
is obtained on the singular boundary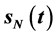 . In particular, consider the mathematical model with only a singular boundary, the maximum value in the interval
. In particular, consider the mathematical model with only a singular boundary, the maximum value in the interval 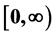 of solution
of solution 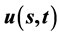 on the singular boundary
on the singular boundary 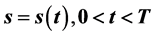 that is,
that is, . The free boundary problem of IIIA and IIIB about Black Scholes equation are all solved. At the same time to obtain exponential function curve
. The free boundary problem of IIIA and IIIB about Black Scholes equation are all solved. At the same time to obtain exponential function curve 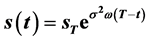 of the free boundary, and singular boundary coincides, so the curve
of the free boundary, and singular boundary coincides, so the curve  is American option implement best boundary.
is American option implement best boundary.
Keywords:Optimal Implementation Boundary, Free Boundary Problem, Singular Inner Boundary, Black-Scholes Equation

具有多条奇异内边界的Black-Scholes方程数学模型的连续有界正解
吴小庆
西南石油大学理学院,四川 成都
Email: wuxiaoqing_swpu@163.com
收稿日期:2016年7月12日;录用日期:2016年8月6日;发布日期:2016年8月9日

摘 要
本文建立了Black-Scholes方程在区域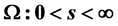 ,
,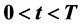 具有多条奇异内边界
具有多条奇异内边界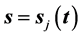 ,
,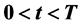 ;
;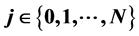 的数学模型,引入广义特征函数法获得了数学模型的精确解
的数学模型,引入广义特征函数法获得了数学模型的精确解 ,并进一步获得奇异内边界是指数函数曲线
,并进一步获得奇异内边界是指数函数曲线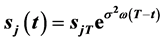 ,
,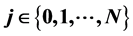 ,证明了在任意时刻
,证明了在任意时刻 ,函数
,函数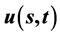 在闭区间
在闭区间 中的最大值在奇异内边界
中的最大值在奇异内边界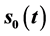 上取得,区间
上取得,区间 中的最大值在奇异内边界
中的最大值在奇异内边界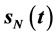 上取得。特别地,考虑在区域
上取得。特别地,考虑在区域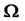 内仅有一条奇异内边界
内仅有一条奇异内边界 ,
,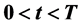 的数学模型,获得了奇异内边界是指数函数曲线
的数学模型,获得了奇异内边界是指数函数曲线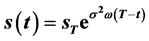 ,证明了:解在奇异内边界
,证明了:解在奇异内边界 ,
,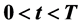 取最大值,即
取最大值,即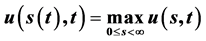 ;且问题IIIA和IIIB的自由边界与奇异内边界重合,指数函数曲线
;且问题IIIA和IIIB的自由边界与奇异内边界重合,指数函数曲线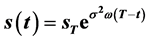 就是美式期权最佳实施边界。
就是美式期权最佳实施边界。
关键词 :最佳实施边界,自由边界问题,奇异内边界,Black-Scholes方程

1. 引言
美式期权合约中具有提前实施的条款,因此最佳实施边界的确定对于美式期权具有特殊意义。在美式期权定价研究中,需要研究Black-Scholes方程的自由边界问题。姜礼尚 [1] 依据偏微分方程理论对最佳实施边界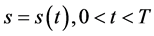 作了很多深入的研究,得到很多重要的结论。其中包括
作了很多深入的研究,得到很多重要的结论。其中包括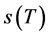 的位置,
的位置, 的单调性,
的单调性,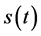 的上下界以及
的上下界以及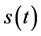 的凸性等,并给出了
的凸性等,并给出了 在
在 附近的渐近表达式。这些结果增加了对最佳实施边界的认识,对美式期权定价的数值计祘产生了重要的影响。本文建立了Black-Scholes方程在区域
附近的渐近表达式。这些结果增加了对最佳实施边界的认识,对美式期权定价的数值计祘产生了重要的影响。本文建立了Black-Scholes方程在区域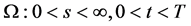 具有多条奇异内边界
具有多条奇异内边界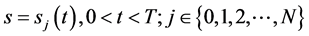 的数学模型,引入广义特征函数法获得了数学模型的精确解
的数学模型,引入广义特征函数法获得了数学模型的精确解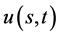 的表达式。并获得奇异内边界的指数函数表达式
的表达式。并获得奇异内边界的指数函数表达式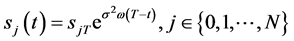 ,且满足
,且满足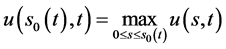 ,
,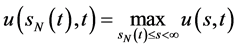 。特别地,考虑在
。特别地,考虑在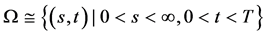 内仅有一条奇异内边界
内仅有一条奇异内边界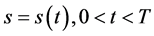 的数学模型,解在奇异内边界
的数学模型,解在奇异内边界 取最大值,即
取最大值,即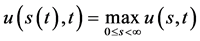 ;同时获得了Black-Scholes方程的自由边界问题IIIA和自由边界问题IIIB的自由边界的表达式
;同时获得了Black-Scholes方程的自由边界问题IIIA和自由边界问题IIIB的自由边界的表达式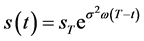 ,问题IIIA和IIIB的自由边界与奇异内边界重合,奇异内边界就是美式期权最佳实施边界。
,问题IIIA和IIIB的自由边界与奇异内边界重合,奇异内边界就是美式期权最佳实施边界。
2. 主要结果
2.1. Black-Scholes方程在区域 具有多条奇异内边界
具有多条奇异内边界 的终值问题数学模型I肑研究
的终值问题数学模型I肑研究
Black-Scholes方程
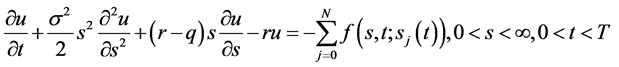 (0)
(0)
引入微分算子
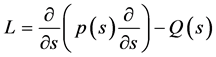
其中
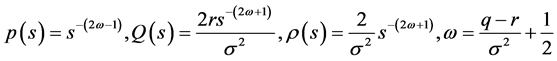
Black-Scholes方程的等价形式是

于是得到数学模型I(Black-Scholes方程具有多条奇异内边界的终值问题)
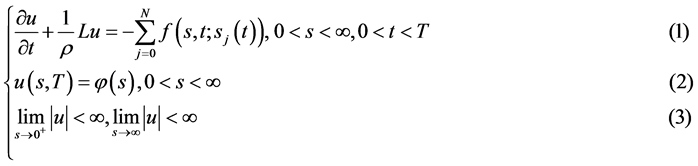
其中: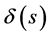 为Dirac函数;
为Dirac函数;
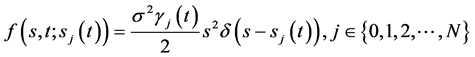 (4)
(4)
微分算子
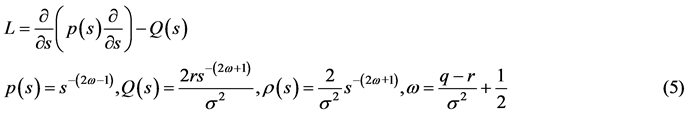
数学模型I.1(Black-Scholes方程的终值问题)
 (6)
(6)
数学模型I.2 (Black-Scholes方程具有多条奇异内边界带齐次终值条件的终值问题)
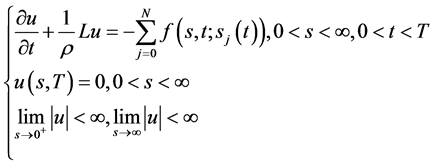 (7)
(7)
2.1.1. Black-Scholes方程在区域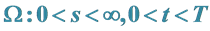 具有多条奇异内边界
具有多条奇异内边界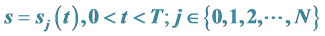 的终值问题的数学模型I的结果
的终值问题的数学模型I的结果
记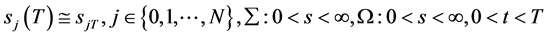
定理1 (具有多条奇异内边界的Black-Scholes方程终值问题解的存在定理):若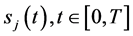 为充分光滑的单调函数,
为充分光滑的单调函数, ,
,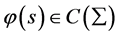 ,则数学模型I有精确解:
,则数学模型I有精确解:
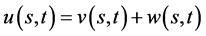
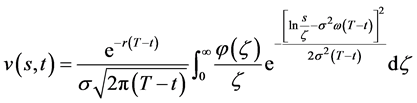 (8)
(8)
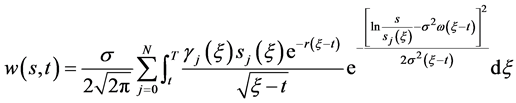 (9)
(9)
其中(8)式是数学模型I.1的解;(9)式是数学模型I.2的解。
附注1:数学模型I.1中,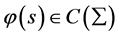 的条件可以削弱,
的条件可以削弱,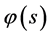 可以是广义函数,公式仍成立。例如,若
可以是广义函数,公式仍成立。例如,若 ,利用d-函数的积分性质即有
,利用d-函数的积分性质即有
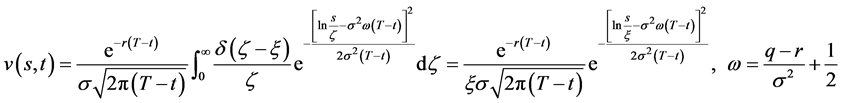 (10)
(10)
上式的结果与文献 [1] 中l32页的结果完全一致。
附注2:数学模型I.2中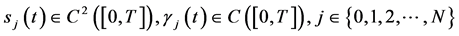 由公式(9)利用换元积分法,令
由公式(9)利用换元积分法,令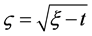 可以得到
可以得到
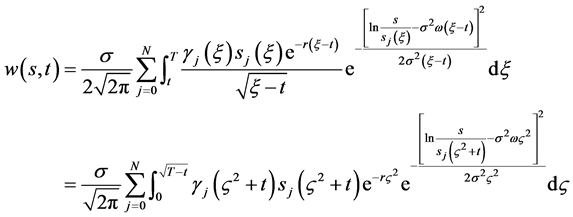
再利用积分中值定理,当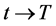 ,有
,有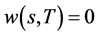 ,满足齐次终值条件。
,满足齐次终值条件。 也可以是广义函数,公式仍成立。例如,
也可以是广义函数,公式仍成立。例如,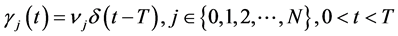 ,由公式(9)立即可得
,由公式(9)立即可得
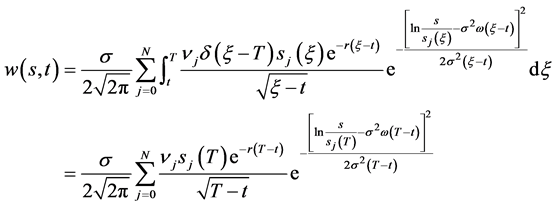 (11)
(11)
2.1.2. Black-Scholes方程数学模型I的求解过程
先考虑特征值问题
 (12)
(12)
这是关于尤拉方程在半无界区间的奇异施图姆-刘维尔问题。
尤拉方程的特解形式为 ,代入方程即有
,代入方程即有
特征根
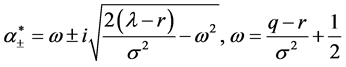 (13)
(13)
即有
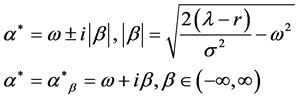 (14)
(14)
于是得到特征值
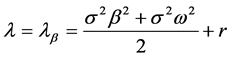 (15)
(15)
特征函数
 (16)
(16)
由于
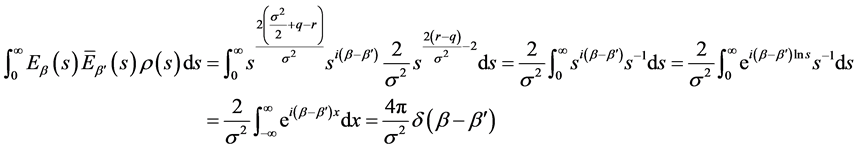
即知特征函数系是半无界区间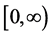 上带权函数
上带权函数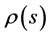 的正交系。
的正交系。
正交关系
 (17)
(17)
将定义在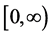 的连续函数
的连续函数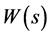 可以展为特征函数的积分形式
可以展为特征函数的积分形式
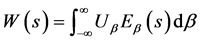 (18)
(18)
由正交关系
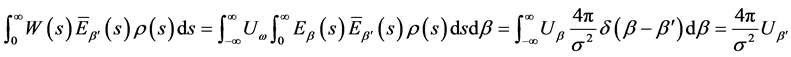
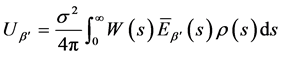
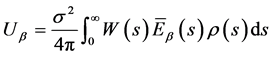 (19)
(19)
由(18),(19)这一对关系式可以引入广义特征函数法 [2] [3] 求解Black-Scholes方程数学模型I。由(18)将模型I解表为
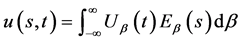 (20)
(20)
由(19)则有
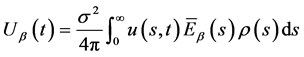 (21)
(21)
 (22)
(22)
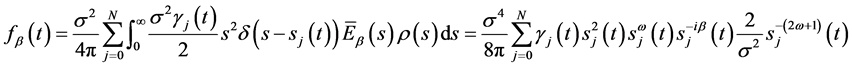
 (23)
(23)
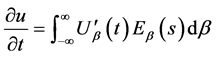 (24)
(24)
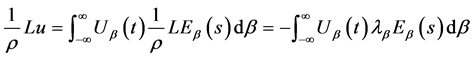 (25)
(25)
将(22),(24),(25)三式代入方程(1)则有

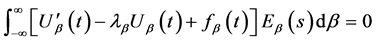 (26)
(26)
于是
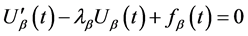 (27)
(27)
由(2)式和(20),(21)有
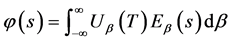 (28)
(28)
 (29)
(29)
得到关于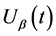 的非齐次常微分方程的终值问题
的非齐次常微分方程的终值问题
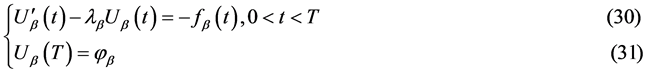
先求对应的齐次常微分方程
 (32)
(32)
的通解。
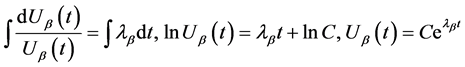 (33)
(33)
用常数变易法求解非齐次常微分方程的终值问题。设满足非齐次常微分方程通解形式为
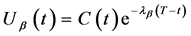 (34)
(34)
其中为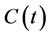 待求函数。
待求函数。
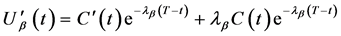
将上式代入非齐次常微分方程(30)即有
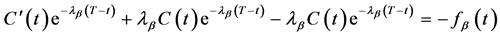
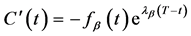 (35)
(35)
对上式在区间 上积分
上积分
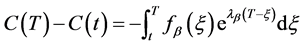
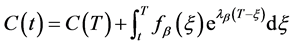 (36)
(36)
再将上式代入(34) 式即有
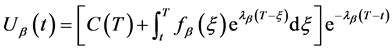 (37)
(37)
利用(31)即有
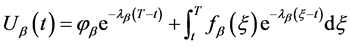 (38)
(38)
将上式代入(20)式即有
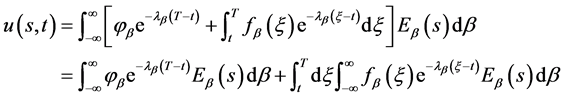 (39)
(39)
其中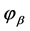 由(29),
由(29), 由(23)确定,即有
由(23)确定,即有
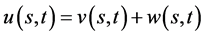 (40)
(40)
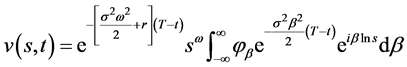 (40.1)
(40.1)
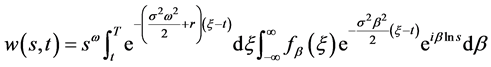 (40.2)
(40.2)
又
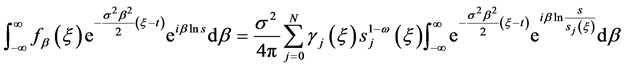
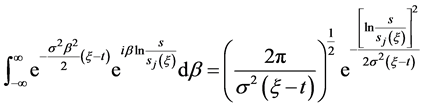 (41)
(41)
利用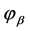 的表达式(29)即有
的表达式(29)即有
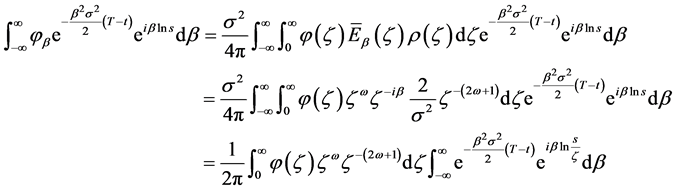
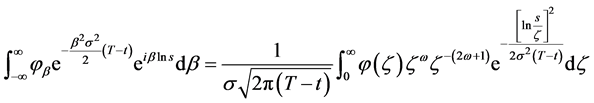 (42)
(42)
将(41),(42)代入(40)得到
 (43)
(43)
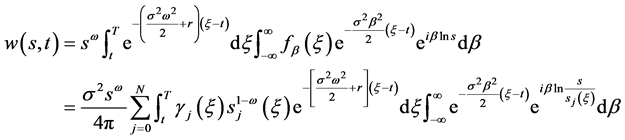
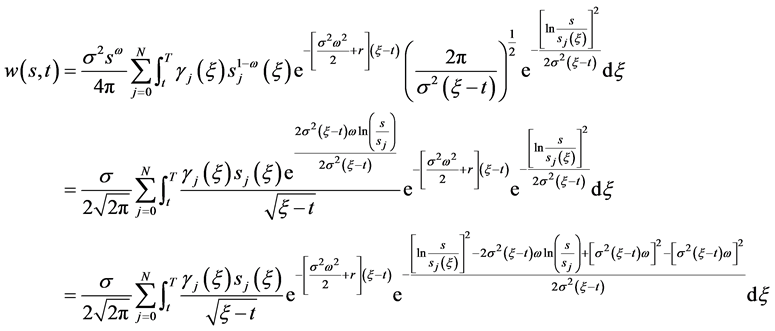
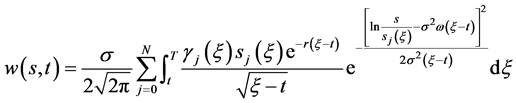 (44)
(44)
即数学模型I (Black-Scholes方程具有多条奇异内边界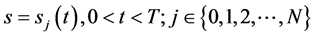 的终值问题)的解
的终值问题)的解
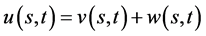 (45)
(45)
其中: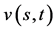 由(43)式给出,
由(43)式给出, 由(44)式给出。
由(44)式给出。
2.1.3. Black-Scholes方程N+1条奇异内边界的确定
定解问题II (Black-Scholes方程确定N+1条奇异内边界的数学模型):
求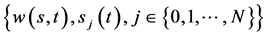 ,使其满足
,使其满足
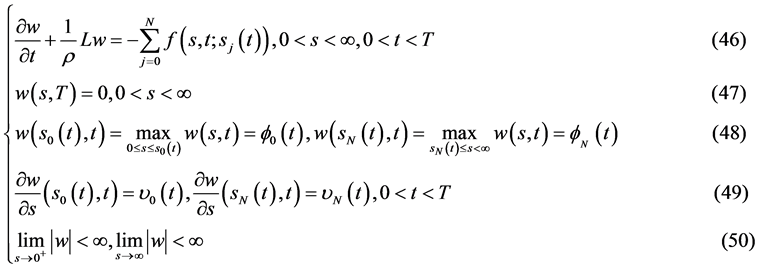
定理2:若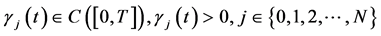 ;
;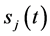 为充分光滑的单调函数,
为充分光滑的单调函数,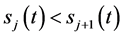 ,
, ,则定解问题II有连续有界的精确解
,则定解问题II有连续有界的精确解
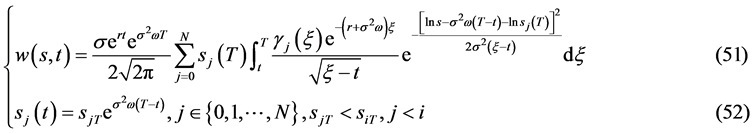
问题II有解的相容性条件是
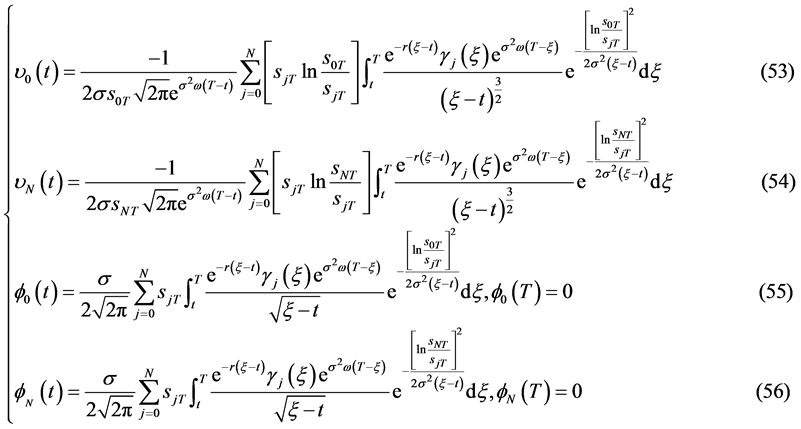
其中 。
。
证明:数学模型I.2的解即(51),记为
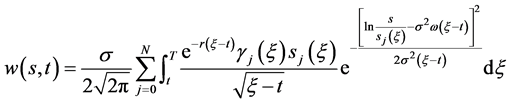 (57)
(57)
它已满足(46),(47),(50)三式。由(57)对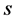 求偏导,
求偏导,
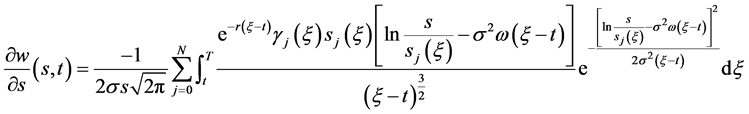 (58)
(58)
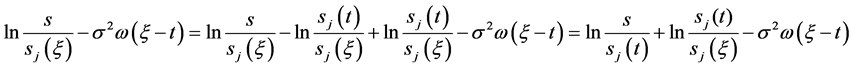 (59)
(59)
若令
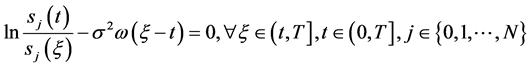 (60)
(60)
则有
 (61)
(61)
下面建立四个引理2.1~引理2.4来完成定理2的证明。
引理2.1:若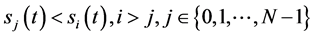 且(60)式成立,则有
且(60)式成立,则有
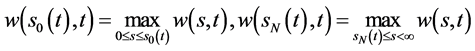 。
。
证明:若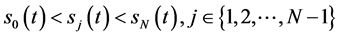 且(60)成立,有(61)成立,再由(58),则有
且(60)成立,有(61)成立,再由(58),则有
 (62)
(62)
1)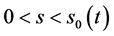 ,
,
由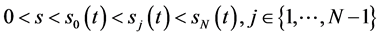 ,
,
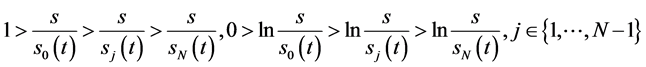
即当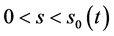 有
有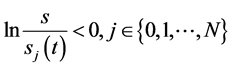 ;再由(62)式即有
;再由(62)式即有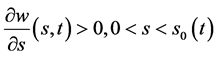 ,从而
,从而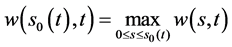 。
。
2) 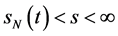
由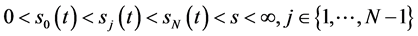 ,
,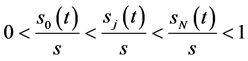 ,
, ,
,
当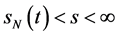 ,有
,有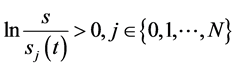 ;再由(62)式即有
;再由(62)式即有 ,从而
,从而 。
。
引理2.2:(60)式: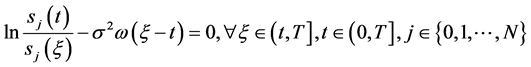
成立的充要条件为
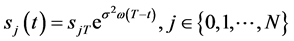 (63)
(63)
证明:1) 必要性:若(60)式成立,
由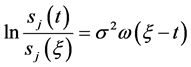 ,即有
,即有 ,
,
故
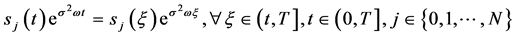 (64)
(64)
记
 (65)
(65)
由(64)式即知
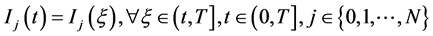 (66)
(66)
让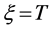 即有
即有
 (67)
(67)
干是有(63)式成立。
2) 充分性:由(63)式成立,则

即(60)式成立。
引理2.3:若 由(63)式给出,条件
由(63)式给出,条件 与条件
与条件 等价。
等价。
引理2.4:若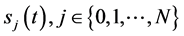 由(63)式给出,且
由(63)式给出,且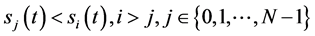 ,则有
,则有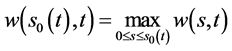 ,
,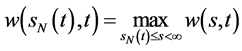 。
。
证明:若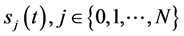 由(63)式给出,且
由(63)式给出,且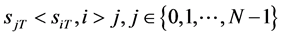 ,由引理2.3推出引理2.1的条件成立,从而由引理2.1得到
,由引理2.3推出引理2.1的条件成立,从而由引理2.1得到 ,
,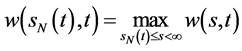 。
。
由(48),(49),(57),(62),(63)式容易验证问题II有解的相容性条件是(53)~(56)式。(63)式代入(57)式即有(51)式。证毕。
自由边界问题IIA (Black-Scholes方程在区域 上的齐次终值条件的自由边界问题):
上的齐次终值条件的自由边界问题):
求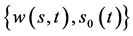 ,使其满足
,使其满足
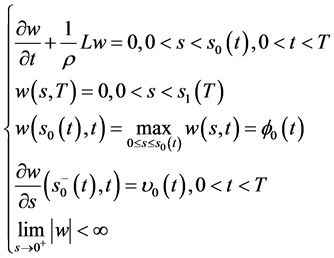 (68)
(68)
推论2.1 (Black-Scholes方程在区域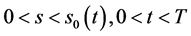 上的自由边界问题):若
上的自由边界问题):若
1)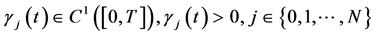 ,
,
2) 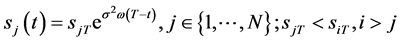
则自由边界问题IIA的连续有界的精确解为
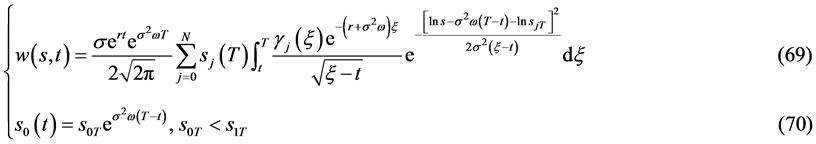
有解的相容性条件为
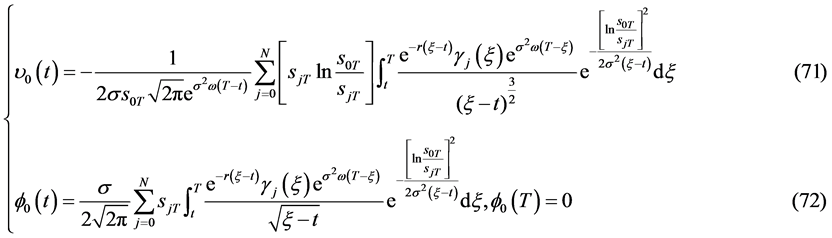
自由边界问题IIB (Black-Scholes方程在区域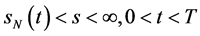 上的齐次终值条件的自由边界问题):求
上的齐次终值条件的自由边界问题):求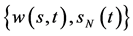 ,使其满足
,使其满足
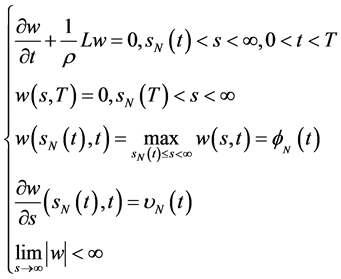 (73)
(73)
推论2.2 (Black-Scholes方程在区域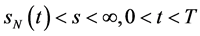 上的自由边界问题IIB):若
上的自由边界问题IIB):若
1)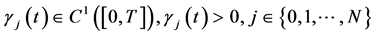 ,
,
2)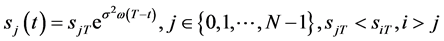 ;
;
则自由边界问题IIB的连续有界的精确解为
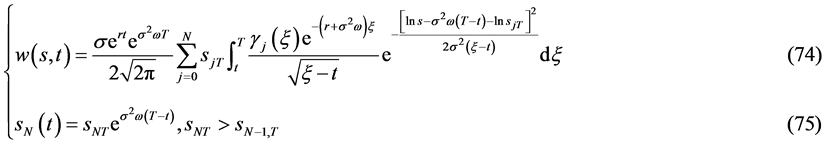
有解的相容性条件为
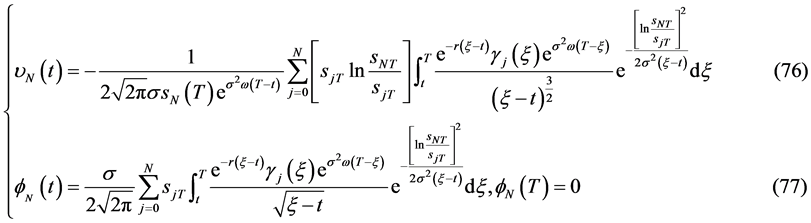
引理2.5:若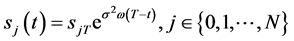 ,且
,且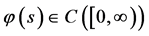
1) 当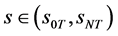 ,
,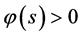 ,当
,当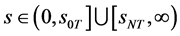 ,
,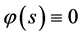 ;则数学模型I.1 (Black-Scholes方程的终值问题)的解
;则数学模型I.1 (Black-Scholes方程的终值问题)的解
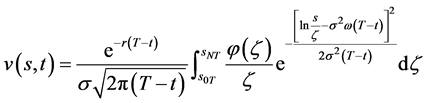 (78)
(78)
且解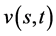 满足
满足 ,
, 。
。
2) 当 ,
,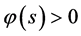 ,当
,当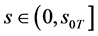 ,
,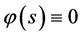 ;则数学模型I.1 (Black-Scholes方程的终值问题)的解
;则数学模型I.1 (Black-Scholes方程的终值问题)的解
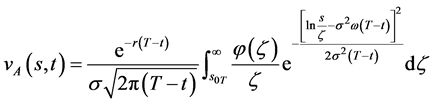 (79)
(79)
且解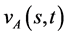 满足
满足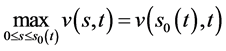 。
。
3) 当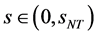 ,
,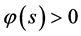 ,当
,当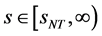 ,
,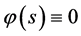 ;则数学模型I.1 (Black-Scholes方程的终值问题)的解
;则数学模型I.1 (Black-Scholes方程的终值问题)的解
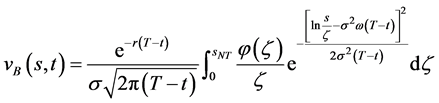 (80)
(80)
且解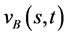 满足
满足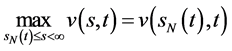 。
。
证明:1) 当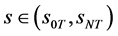 ,
,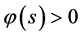 ,当
,当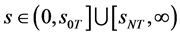 ,
, ;由数学模型I.1 (Black-Scholes方程的终值问题)的解(8)式即有
;由数学模型I.1 (Black-Scholes方程的终值问题)的解(8)式即有
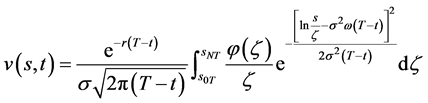 (81)
(81)
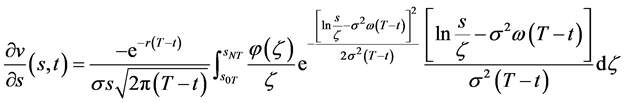 (82)
(82)
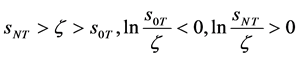 (83)
(83)
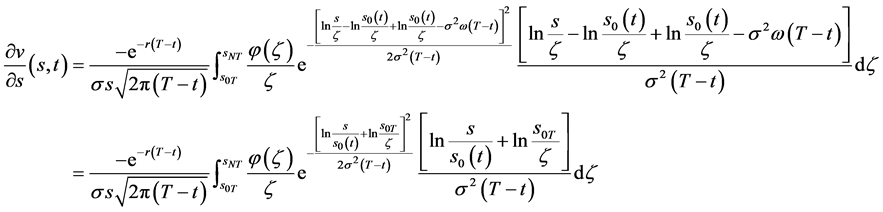 (84)
(84)
当 有
有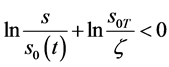 ,由(84)式有
,由(84)式有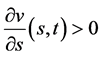 ,从而
,从而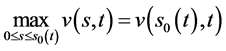 。
。
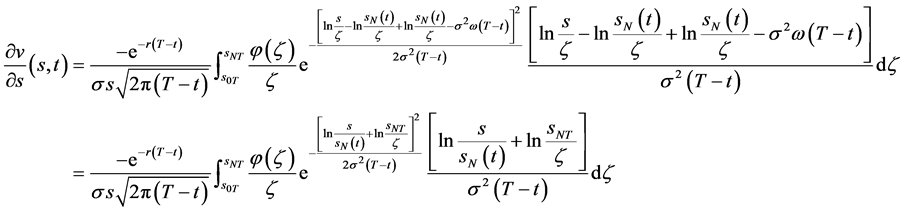
(85)
当 有
有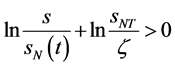 ,由(85)式
,由(85)式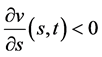 ,从而
,从而 。
。
2) 当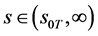 ,
,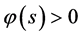 ,当
,当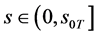 ,
, ;则数学模型I.1 (Black-Scholes方程的终值问题)的解由(79)式给出。由(79)式有
;则数学模型I.1 (Black-Scholes方程的终值问题)的解由(79)式给出。由(79)式有

(86)
当 有
有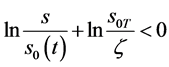 ,由(86)式有
,由(86)式有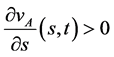 ,从而
,从而 。
。
3) 当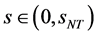 ,
,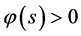 ,当
,当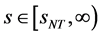 ,
,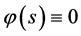 ;则数学模型I.1 (Black-Scholes方程的终值问题)的解由(80)式给出。由(80)式有
;则数学模型I.1 (Black-Scholes方程的终值问题)的解由(80)式给出。由(80)式有
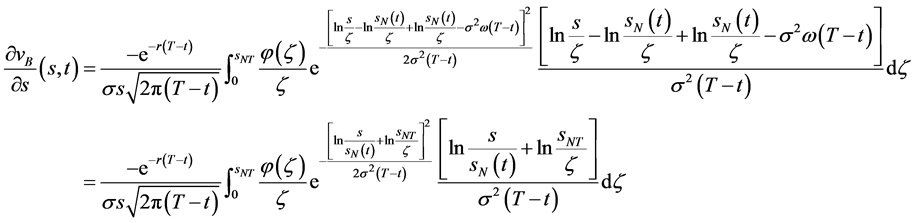 (87)
(87)
当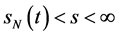 有
有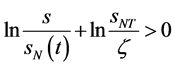 ,由(87)式有
,由(87)式有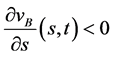 ,从而
,从而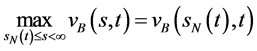 。证毕。
。证毕。
定理3:若
1) 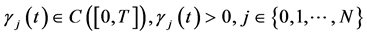
2) 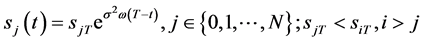
3)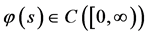 且当
且当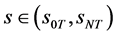 ,
,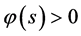 ,当
,当 ,
, ;
;
则数学模型I有连续有界的精确解
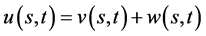 (88)
(88)
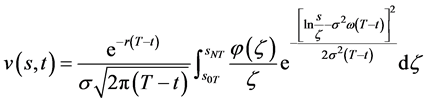 (89)
(89)
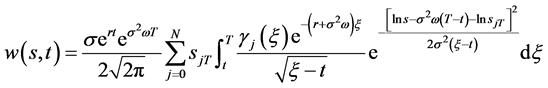 (90)
(90)
且满足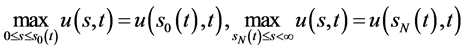 。
。
证明:由定理2有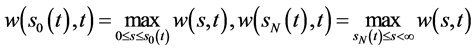
由引理2.5有 ,
, ;
;
从而
 ,
,
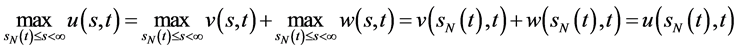 .
.
证毕。
自由边界问题IA (Black-Scholes方程在区域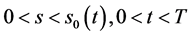 上的非齐次终值条件的自由边界问题):
上的非齐次终值条件的自由边界问题):
求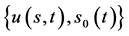 ,使其满足
,使其满足
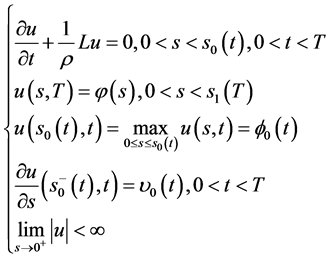 (91)
(91)
推论3.1:若
1) 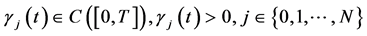
2) 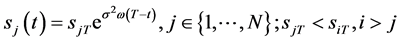
3)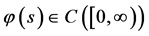 且当
且当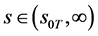 ,
,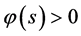 ,当
,当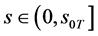 ,
,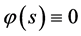 ;
;
则自由边界问题IA有连续有界的精确解

其中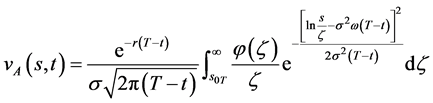 (94)
(94)
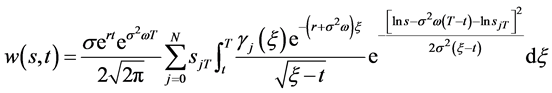 (95)
(95)
有解的相容性条件为
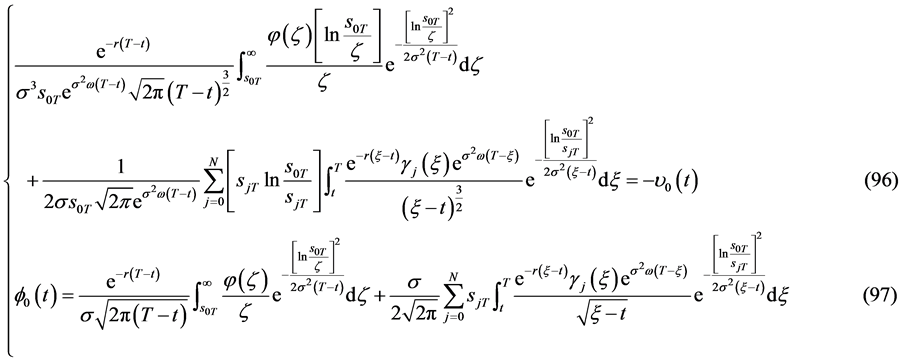
自由边界问题IB (Black-Scholes方程在区域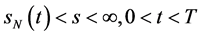 上的非齐次终值条件的自由边界问题):求
上的非齐次终值条件的自由边界问题):求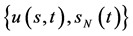 ,使其满足
,使其满足
 (98)
(98)
推论3.2:若
1) 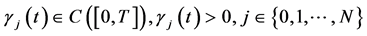
2) 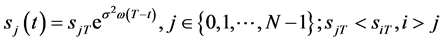
3)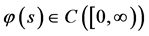 且当
且当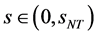 ,
,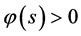 ,当
,当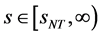 ,
,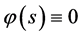 ;
;
则自由边界问题IB有连续有界的精确解

其中
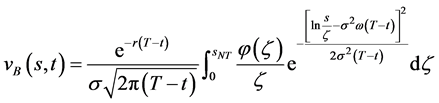 (101)
(101)
 (102)
(102)
有解的相容性条件为
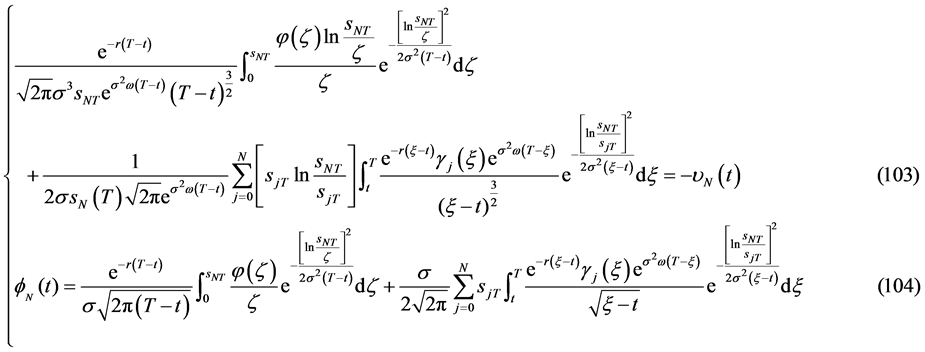
附注3:非齐次终值条件的自由边界问题IA的解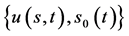 与齐次终值条件的自由边界问题IIA的解
与齐次终值条件的自由边界问题IIA的解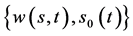 满足
满足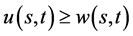 ;但自由边界问题IA和IIA所得到的自由边界
;但自由边界问题IA和IIA所得到的自由边界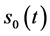 是一致的。
是一致的。
非齐次终值条件的自由边界问题IB的解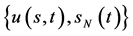 与齐次终值条件的自由边界问题IIB的解
与齐次终值条件的自由边界问题IIB的解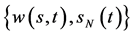 满足
满足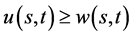 ;但自由边界问题IB和IIB所得到的自由边界
;但自由边界问题IB和IIB所得到的自由边界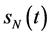 是一致的。
是一致的。
2.2. Black-Scholes方程在区域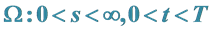 有且仅有一条奇异内边界
有且仅有一条奇异内边界 的齐次终值问题数学模型III
的齐次终值问题数学模型III
数学模型III (有且仅有一条奇异内边界的齐次终值问题):
求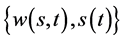 ,使其满足
,使其满足

其中:
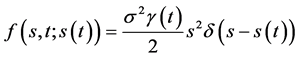 (110)
(110)
定理4:若 为充分光滑的单调函数,
为充分光滑的单调函数,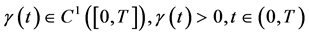 ,则数学模型III的精确解
,则数学模型III的精确解
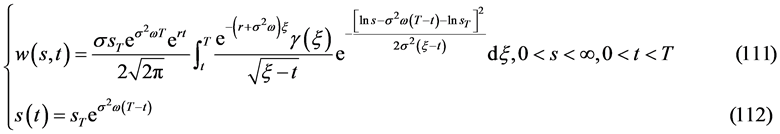
有解的相容性条件是
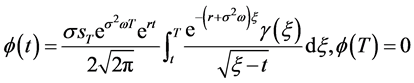 (113)
(113)
证明:由定理2中令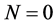 ,
,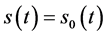 ,
,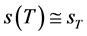 即得(111),(112)。
即得(111),(112)。
问题II有解的相容性条件(55)即得数学模型III有解的相容条件(113)。
问题II有解的相容性条件(53)推出应有条件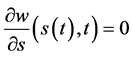 ,亊实上由(111)关于
,亊实上由(111)关于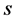 求偏导得到
求偏导得到
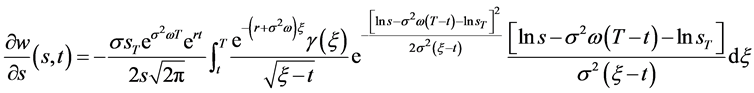 (114)
(114)
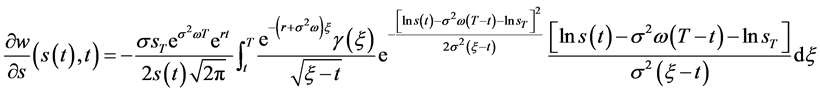 (115)
(115)
由(112)式两边取对数,即得
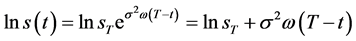 (116)
(116)
将(116)式代入(115)式即有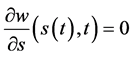 成立。由(114),(116)两式易得
成立。由(114),(116)两式易得
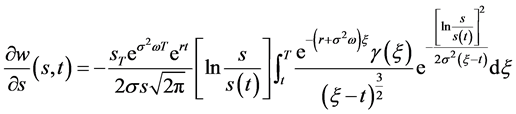 (117)
(117)
当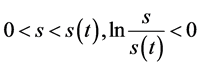 ,由(117)式得到
,由(117)式得到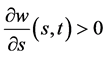 从而
从而
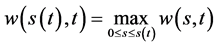 (118)
(118)
当 ,由(117)式得到
,由(117)式得到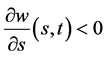 从而
从而
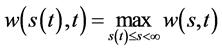 (119)
(119)
由(118),(119)两式即有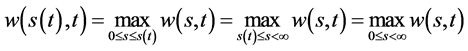 。证毕。
。证毕。
定理5 (数学模型III解的性质定理):若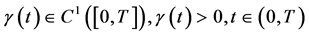 由(111),(112)给出的精确解满足
由(111),(112)给出的精确解满足
1) 内边界 是指数函数,
是指数函数,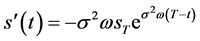 。当
。当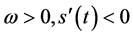 ,
,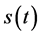 为充分光滑的单调减函数;当
为充分光滑的单调减函数;当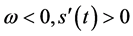 ,
, 为充分光滑的单调增函数。
为充分光滑的单调增函数。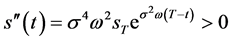 。
。
2) 解函数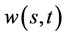 在内边界
在内边界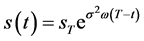 上具有很好的光滑性:
上具有很好的光滑性:
 。且满足
。且满足
 (120)
(120)
证明:显然有 。由(117)式
。由(117)式
1) 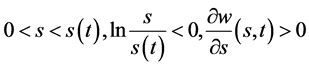

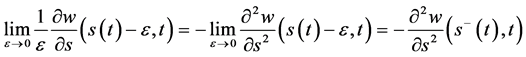
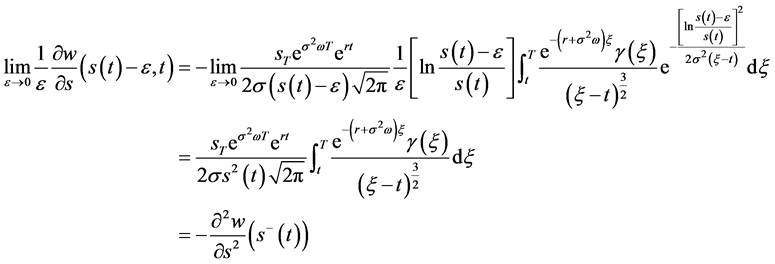
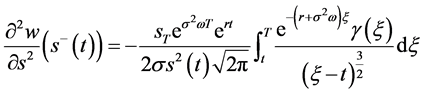 (121)
(121)
2) 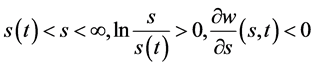

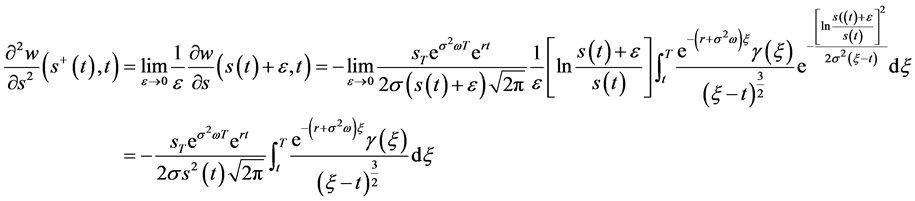
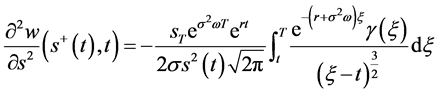 (122)
(122)
由(121),(122)即是(120)。对(111)应用换元积分法即可变形为含参变量的变上限积分形式
 (123)
(123)
记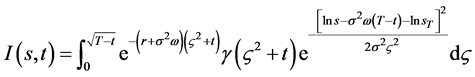 (124)
(124)
 (125)
(125)
应用含参变量的变上限积分的求导公式即得
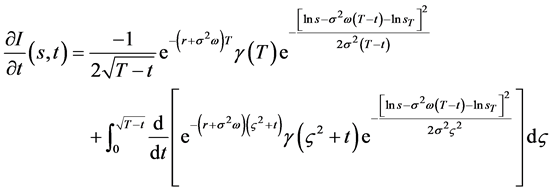 (126)
(126)
由(126)式即知当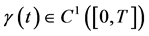 有
有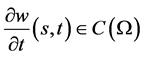 。证毕。
。证毕。
自由边界问题IIIA (Black-Scholes方程在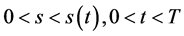 上的自由边界问题):求
上的自由边界问题):求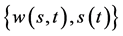 ,使其满足
,使其满足
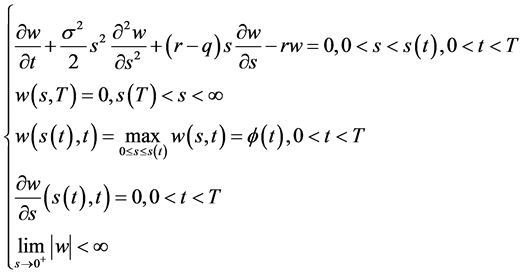 (127)
(127)
推论3.1:若 为充分光滑的单调函数,
为充分光滑的单调函数,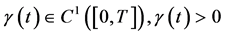 ,
,
则自由边界问题IIIA有连续有界的精确解
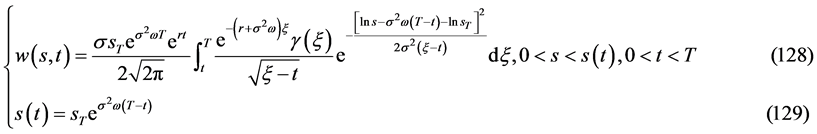
有解的相容性条件是
 (130)
(130)
自由边界问题IIIB (Black-Scholes方程在区域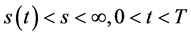 上的自由边界问题):求
上的自由边界问题):求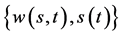 ,使其满足
,使其满足
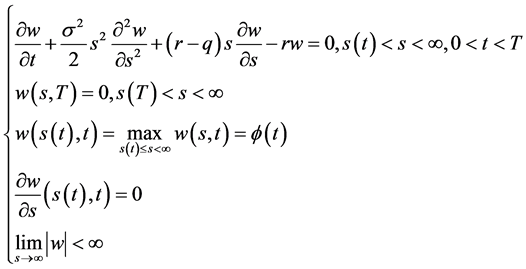 (131)
(131)
推论3.2:若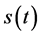 为充分光滑的单调函数,
为充分光滑的单调函数,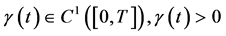 ,
,
则自由边界问题IIIB有连续有界的精确解
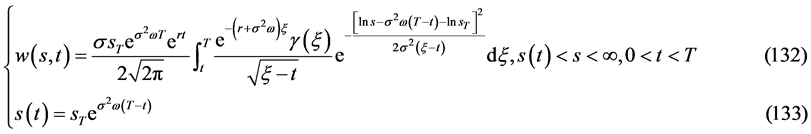
有解的相容性条件是
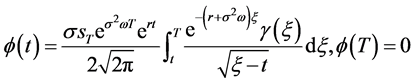 (134)
(134)
定理6 (数学模型III的奇异内边界与问题IIIA,IIIB的自由边界三线合一定理):
当 为充分光滑的单调函数,
为充分光滑的单调函数,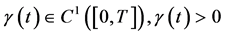 ,且数学模型III与问题IIIA,IIIB中的边值函数满足条件(134),则数学模型III的奇异内边界问题与问题IIIA,IIIB的解具有相同的表达式
,且数学模型III与问题IIIA,IIIB中的边值函数满足条件(134),则数学模型III的奇异内边界问题与问题IIIA,IIIB的解具有相同的表达式
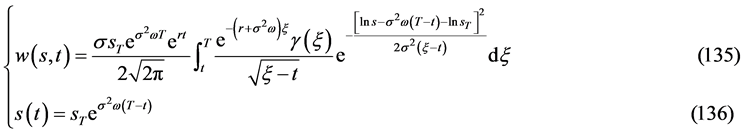
数学模型III的奇异内边界与问题IIIA,IIIB的自由边界三曲线重合成一条指数函数曲线 ;数学模型III的解函数是问题IIIA和IIIB的解函数的共同连续开拓,问题IIIA和IIIB的解函数是数学模型III的解函数在它们各自的定义域内的限制。
;数学模型III的解函数是问题IIIA和IIIB的解函数的共同连续开拓,问题IIIA和IIIB的解函数是数学模型III的解函数在它们各自的定义域内的限制。
附注4:关于条件(134),也可以称为数学模型III有解的相容性条件,若给定函数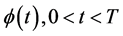 ,则条件(134)是关于函数
,则条件(134)是关于函数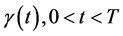 的第一类Volterra积分方程 [4] ;函数
的第一类Volterra积分方程 [4] ;函数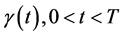 必须是满足积分方程(134)的解。
必须是满足积分方程(134)的解。
例如,若边值函数由(137)式给出,容易验证(138)给出的 是满足积分方程(134)的解。若
是满足积分方程(134)的解。若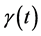 由(138)式定义,则相应的边值函数
由(138)式定义,则相应的边值函数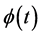 必须使(137)式成立。
必须使(137)式成立。
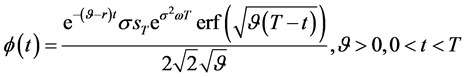 (137)
(137)
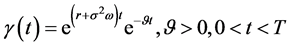 (138)
(138)
其中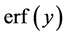 为误差函数。
为误差函数。
附注5:若数学模型III的奇异内边界与问题IIIA,IIIB中的边值函数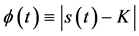 ,则
,则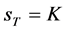 ,且有解的相容性条件是函数
,且有解的相容性条件是函数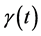 为第一类Volterra积分方程(139)的解。
为第一类Volterra积分方程(139)的解。
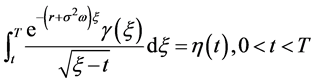 (139)
(139)
其中
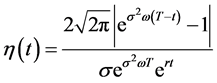 (140)
(140)
3. 结论
I简单期权价格曲面的情形,即Black-Scholes方程在区域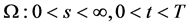 内有且仅有一条奇异内边界的情形。定理6的结果得到数学模型III的期权价格函数对任意时刻
内有且仅有一条奇异内边界的情形。定理6的结果得到数学模型III的期权价格函数对任意时刻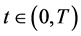 ,在奇异内边界
,在奇异内边界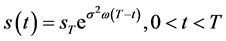 上取最大值
上取最大值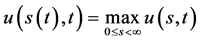 ,且数学模型III的奇异内边界与问题IIIA和IIIB的自由边界三曲线重合。对简单期权价格曲面而言,数学模型III的奇异内边界与问题IIIA和IIIB的自由边界都是最佳实施边界。
,且数学模型III的奇异内边界与问题IIIA和IIIB的自由边界三曲线重合。对简单期权价格曲面而言,数学模型III的奇异内边界与问题IIIA和IIIB的自由边界都是最佳实施边界。
II复杂期权价格曲面的情形,即Black-Scholes方程在区域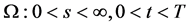 具有N+1条奇异内边界
具有N+1条奇异内边界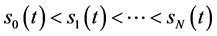 的情形。由定理2期权价格函数
的情形。由定理2期权价格函数 满足条件
满足条件 ,
,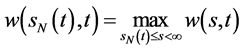 。当
。当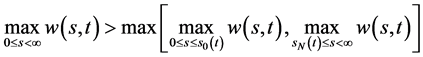 时,问题IIA的自由边界
时,问题IIA的自由边界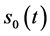 与问题IIB的自由边界
与问题IIB的自由边界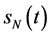 都不是最佳实施边界;当
都不是最佳实施边界;当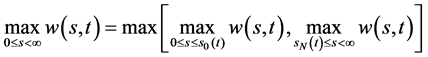 时,问题IIA的自由边界
时,问题IIA的自由边界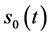 与问题IIB的自由边界
与问题IIB的自由边界 有可能成为最佳实施边界。在复杂多变的情况下,一般不能用问题IIA的自由边界
有可能成为最佳实施边界。在复杂多变的情况下,一般不能用问题IIA的自由边界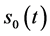 ,或问题IIB的自由边界
,或问题IIB的自由边界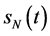 的计祘结果去推断其为美式期权最佳实施边界。单独考虑自由边界问题IIA或IIB所得到的自由边界的计祘结果皆有可能与真实情况的最佳实施边界相差很远。
的计祘结果去推断其为美式期权最佳实施边界。单独考虑自由边界问题IIA或IIB所得到的自由边界的计祘结果皆有可能与真实情况的最佳实施边界相差很远。
文章引用
吴小庆. 具有多条奇异内边界的Black-Scholes方程数学模型的连续有界正解
Continuous Bounded Positive Solutions of Black-Scholes Equations with Multiple Singular Inner Boundary[J]. 理论数学, 2016, 06(04): 368-390. http://dx.doi.org/10.12677/PM.2016.64052
参考文献 (References)