Pure Mathematics
Vol.
08
No.
06
(
2018
), Article ID:
27523
,
6
pages
10.12677/PM.2018.86087
The United Solution for Positive and Inverse Problems of One-Dimensional Boussinesq Equation
Yuhong Jin, Leihao Zuo*
Department of Basic Courses, Naval University of Engineering, Wuhan Hubei

Received: Oct. 19th, 2018; accepted: Oct. 31st, 2018; published: Nov. 13th, 2018

ABSTRACT
In this paper, the inverse problem and the positive problem of the one-dimensional Boussinesq equation are solved jointly by using the finite difference method. In the solving process, the nonlinear least square method is used for optimization. The approximate solution is consistent with the truth value.
Keywords:Inverse Problems, Boussinesq Equation, Finite Difference Method, Nonlinear Least Square Method
一维Boussinesq方程反问题与正问题 的联合求解
金裕红,左雷浩*
海军工程大学基础部,湖北 武汉

收稿日期:2018年10月19日;录用日期:2018年10月31日;发布日期:2018年11月13日

摘 要
本文通过有限差分法对一维Boussinesq方程反问题和正问题进行联合求解,求解过程中利用非线性最小二乘法进行了优化,得到的近似解与真值的基本吻合。
关键词 :反问题,Boussinesq方程,有限差分法,非线性最小二乘法

Copyright © 2018 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 反问题的提出
伴随着科学技术的发展,人类生存环境也遭受了不同程度的破坏,尤其是工业污染物的排放使得地下水资源受到了严重的污染。研究地下水渗透模型,控制地下水污染等课题变得刻不容缓 [1]。在处理渗透扩散问题时,我们往往将其归结为偏微分方程反问题。所谓偏微分方程反问题,是指微分方程中原来已知的系数或者定解问题中的初始条件、边界条件等变成了待定的值,即原定解问题的一个或者几个已知量由已知变成未知,而原方程中的未知量仍然是未知量,或仅已知与未知量有关的某些附加条件,我们的研究内容就是通过微分方程、已知的定解条件和附加条件来确定问题中的未知量。
地下水运动情况可以用Boussinesq方程来描述,方程以及定解条件为
式中h表示水头; 为入渗强度; 为渗透系数,表示岩层的透水性的大小,在均匀的岩层中,渗透系数 和区域坐标无关,为常数,在非均匀岩层中,渗透系数 为空间位置的函数,随着区域坐标变化而变化。如果给定了 的值,且满足所需要的光滑性条件,我们由偏微分的知识可以知道该问题的解存在且唯一。此时,该问题为正问题 [2]。
如果只给定了 的表达式,而 都是未知,但是给定了 在某时刻的近似值(测量值),要求我们确定渗透系数 ,来求解上述问题,这时的问题就是系数反演问题。实际工程中往往渗透系数是未知的,通常通过获得更多的信息或者测量数据来反演系数 ,这类系数反演问题是偏微分方程反问题的重要课题,也是工程技术领域的重要课题 [3]。
本文利用有限差分法对一维流动的Boussinesq方程渗透系数反演问题进行数值计算。该方程的求解对于潜水含水层水量的计算和评价有重要意义。近年来,不少学者对一维抛物型偏微分方程系数反演问题做了大量研究并提出不少数值计算方法。最为常用的是有限差分法、有限元法、有限体积法和多重网格法 [4]。
有限差分法的思想是用离散的、含有有限个未知量的差分方程去近似代替连续变量的微分方程及边界条件,并把相应的差分方程解作为微分方程的解,因此,差分法需要讨论的问题即构造近似代替定解问题的差分方程,即建立差分格式问题 [5]。自然科学和工程技术领域的许多问题都需要求抛物型方程的数值解。抛物型偏微分方程是重要的数学物理方程,而有限差分法是求解抛物型方程的重要方法,Matlab作为数值计算的重要工具,有丰富的资源可以用于求解抛物型方程。
有限差分方法不仅是偏微分方程数值解的重要方法,而且也是偏微分方程数值解的有效方法。但应用于具体问题时,还需根据具体情况进行分析与处理。在研究与应用中还需要进一步解决如何提高计算速度、计算精度以及差分分解的收敛性等问题。用有限差分方法近似求解偏微分方程问题有多种多样的方法,并且也可以用不同的构造方法来建立这些有限差分方法。
2. 有限差分法
2.1. 差分格式的建立
首先在矩形区域 内研究如下Boussinesq方程的初边值问题
现在考虑 的非线性,为了方便我们进行离散化处理,这里对其进行处理如下,并代入原方程:
下面考虑初边值问题的差分逼近。将上述区域划分为
维网格,取时间步长
和空间步长
,网格节点为 ,用
表示定义在网点
上的函数,
。考虑到
,用
表示定义在网点
上的函数,
。考虑到
边界上的点无法用两点差分格式处理,我们采用三点差分格式,将上述微分方程进行离散化,得到 离散化后的三点数值微分公式表示为:
对应的等式右边:
离散化后的三点数值微分公式表示为:

离散化后的三点数值微分公式:
离散化后的三点数值微分公式:
2.2. 方程组求解
通过对上述方程的离散化,我们可以得到 个方程,将初始条件和边界条件进行离散化后又得到 个方程,而在以上方程组中,k的离散未知值有m个,h的离散未知值有 个,方程的总个数大于未知量的总个数,所以,一般来说,由于离散化带来的误差影响,得到的关于离散未知值的方程组通常是不相容的,我们可以采用最小二乘法来求解。在Matlab软件中,lsqnonlin解决非线性最小二乘法问题,包含非线性数据的拟合问题,lsqnonlin采用了Levenberg-Marquardt算法,Levenberg-Marquardt算法是求解非线性问题的一个非常好用的算法。
另外由于lsqnonlin函数采用的是迭代法,对迭代初始值有一定的依赖性。因为程序的局限性,不可能搜索无穷大的区间,这样一来,初始值的选择就显得尤为重要。如果最优解离所给初始值比较近,迭代求出该最优解的可能性偏高;如果设定的初始值不理想,离最优解较远,而matlab对于迭代次数及迭代精度都有个默认的设定,这种情况下很可能没有搜到最优解便给出了结果,当然这个结果是在所搜索区间上的最优解而极有可能不是全局最优的。
3. 数值实验
给定参数取值进行数值实验,其中
已经给定,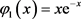 ,
,
。如果给定了
的值,则
可以由方程计算得到。本实验采用
的真值为
,
的真值为
,其中,给定的附加条件为
。
,
,
。如果给定了
的值,则
可以由方程计算得到。本实验采用
的真值为
,
的真值为
,其中,给定的附加条件为
。
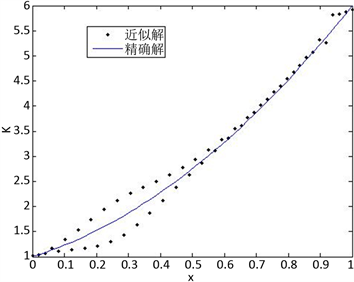
不同数量级的网格密度对方程拟合的精确程度会产生一定的影响,下面将在5 × 5,10 × 10,50 × 50不同网格密度下进行比较(图1~图4)。
通过对实验数据进行误差分析,残差平方和表示实验所得离散数据与参数真值的连续函数的偏差程度;残差平方和除以方程的总个数所得平均残差平方和,平均残差平方和表示离散后的每一个方程与参数真值函数的偏差程度,平均残差平方和也越来越小,说明离散后的每一个方程与参数真值函数越逼近; 表示本文算法得到的离散点最优解与 给定真值 的方差的平均值,代表本算法所的近似解的吻合程度。由表1可以看出,随着网格密度的增加,本算法所得近似解与真值的吻合程度越来越好。
在文献 [6] 中对该方程采用了最佳摄动量法进行求解计算,我们将本文所用最小二乘法所得离散数据、
图1.
图2.
图3.

Figure 4. Comparison
图4. 对比
Table 1. Average residual sum of squares under different grid densities
表1. 不同网格密度下的平均残差平方和
文献 [6] 中最佳摄动量所得近似解与函数真值进行对比,结果如图4所示。由于在计算过程中,作者把未知参数k(x)的函数类型限制为多项式形式,最终所得近似解与真值的吻合程度较高,而在本文中,我们并未对未知函数的类型进行限制,最终导致与其结果有一定的差异。
文章引用
金裕红,左雷浩. 一维Boussinesq方程反问题与正问题的联合求解
The United Solution for Positive and Inverse Problems of One-Dimensional Boussinesq Equation[J]. 理论数学, 2018, 08(06): 650-655. https://doi.org/10.12677/PM.2018.86087
参考文献
- 1. 田娜. 偏微分方程反问题数值解研究与应用[D]: [博士学位论文]. 无锡: 江南大学, 2012.
- 2. 王兵贤, 徐定华, 胡康秀. 一维流动的Boussinesq方程渗流系数反演的变分伴随方法研究[J]. 数学的实践与认识, 2008, 38(20): 194-200.
- 3. 王兵贤, 王泽文, 徐定华, 胡康秀. 二维流Boussinesq方程渗透系数反演的变分伴随方法[J]. 水利水电科技进展, 2010, 30(6): 11-14.
- 4. 张海丽. 非线性抛物型方程若干类反问题的研究[D]: [硕士学位论文]. 杭州: 浙江理工大学, 2010.
- 5. 潘树龙, 孙维夫. 抛物型偏微分方程的多步有限差分法计算方法[J]. 烟台职业学院学报, 2011, 17(1): 76-80.
- 6. 刘春风, 彭亚绵. 偏微分方程并行算法及反问题数值解法[M]. 北京: 清华大学出版社, 2015: 183-185.