Pure Mathematics
Vol.
13
No.
09
(
2023
), Article ID:
72459
,
24
pages
10.12677/PM.2023.139259
带跳多尺度分数布朗运动下欧式期权定价问题
胡静,黄小涛
南京航空航天大学数学学院,江苏 南京
收稿日期:2023年7月29日;录用日期:2023年8月31日;发布日期:2023年9月8日

摘要
为了更合理地描述金融市场里股票等风险资产的“跳跃”、“尖峰厚尾”以及多周期现象,本文通过引入Merton跳跃、分数阶几何布朗运动以及多尺度理论,研究了在标的资产满足带跳多尺度分数阶几何布朗运动的假设下,欧式期权的定价问题。首先,本文证明了多尺度分数阶跳–扩散过程的伊藤公式,利用无套利原理和风险中性原理,得到了欧式期权价格满足的分数阶Black-Scholes方程。另一方面,本文根据分数布朗运动的Girsanov定理,建立了带跳多尺度分数阶布朗运动下风险中性的等价鞅测度,从而利用鞅定价方法得到欧式看涨看跌期权的定价公式及平价公式。最后通过数值模拟证明了该定价模型的科学性。
关键词
欧式期权定价方程,分数布朗运动,Merton跳跃,多尺度布朗运动,等价鞅测度

European Option Pricing Problem Involving Multi-Scale Fractional Brownian Motion with Jump
Jing Hu, Xiaotao Huang
College of Mathematics, Nanjing University of Aeronautics and Astronautics, Nanjing Jiangsu
Received: Jul. 29th, 2023; accepted: Aug. 31st, 2023; published: Sep. 8th, 2023

ABSTRACT
In order to describe more reasonably the “jump”, “spike thick tail” and multi-period phenomenon of stock prices in the financial market, this paper studies the European options pricing problem while the underlying asset satisfies the assumption of jump-diffusion and multi-scale fractional order geometric Brownian motions, by introducing Merton jump, fractional geometric Brownian motion and multi-scale theory respectively. On the one hand, this paper first proves the Ito’s formula for the multi-scale fractional Brownian motion with jumps, then derives the fractional Black-Scholes equation by using the no-arbitrage principle and the risk neutrality principle. On the other hand, based on Girsanov’s theorem of fractional Brownian motion, this paper establishes the risk-neutral equivalent martingale measure for the multi-scale fractional Brownian motion with jumps. And then, this paper obtains the call-put pricing formula and parity formula for European options by using equivalent martingale measure. Finally, numerical simulation proves the scientific nature of the pricing model.
Keywords:European Option Pricing Equation, Fractional Brownian Motion, Merton Jumps, Multiscale Brownian Motion, Equivalent Martingale Measure

Copyright © 2023 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
期权定价问题是金融数学和计量经济学领域的一个重要内容,Black-Scholes模型 [1] 是期权定价问题研究过程中的一个里程碑,其研究者F. Black,M. Scholes在1997年荣获了第二十九届诺贝尔经济学奖,后续期权定价的理论研究基本都是在此基础上展开的。该模型有一个重要前提,标的资产价格必须遵循标准几何布朗运动。但是近年来大量实证研究结果表明,金融市场呈现出一种“尖峰厚尾”的分布,并且股票价格存在着不同程度的自相似性和长期相关性,这些特征与标准的几何布朗运动存在一定的差距,因此一些学者用分数布朗运动来描述标的价格的变化行为。分数布朗运动最初是由Kolmogorov [2] 于1941年在Hilbert空间框架中定义和研究的,并命名为Wiener螺线(helix)。而Mandelbrot和Van Ness [3] 于1968年首次提出“分数布朗运动”这一概念,并给出了分数布朗运动的构造。同时由于分数布朗运动不是半鞅,所以众多学者试图寻找一种新的积分来消除分数布朗运动下的套利。1995年,Lin [4] 提出了有关分数路径依赖型积分概念,这一概念对于解决分数Brown运动的随机积分做出了重要的贡献。另一个关于分数Brown运动的随机积分理论是Wick-Itô型积分理论。2000年,Duncan [5] 等建立了一个关于分数布朗运动的基于Wick乘积的随机积分,称为分形Ito积分。在在分形Ito积分下,Hu和Oksendal [6] 基于Wick乘积和白噪声分析得到分数Wick-Ito-Skorohod积分,证明了这种Ito类型的分数Black-Scholes市场是无套利的,并提出了拟鞅的概念,给出了欧式期权在
时刻的定价公式。随后,Necula [7] 分析了分数布朗运动下的期权市场,并给出了欧式期权在任意时刻
的定价公式。但分数布朗运动的数据并不是恒正的,并不能满足股价是正数的要求。而几何布朗运动(GBM)是随机过程,它的期望值与随机过程的价格是独立的,即过去的价格数据与未来的股价不相关,正符合学者们研究股价问题时的要求。同时几何布朗运动只考虑取值是正数时的情况,而股价也是只取正数,因此正好适用于股价研究。因此许多学者把分数布朗运动和几何布朗运动结合起来,用分数阶几何布朗运动去刻画标的资产的价格运动。如程潘红 [8] 研究了在在分数阶几何布朗运动环境下基于蒙特卡洛方法,定价分析了上证50ETF期权。Ahmadian [9] 假设股票价格服从混合分数阶几何布朗运动,得到了混合分数阶几何布朗运动下亚式彩虹期权的定价公式。王体标 [10] 在市场是完全且无套利的环境下,假定期权价格服从分数阶几何布朗运动的基础上,得出了商品互换的定价公式及其互换期权的精确定价公式。侯营营 [11] 利用时间轴变换法的思想,将几何分数布朗运动近似地转化为分数阶几何布朗运动得到分数欧式幂型期权的定价模型,并讨论了有红利支付的分数欧式看涨期权及相关的性质。
同时在Balck-Scholes模型中,在标的资产的价格服从正态分布,这与实际交易市场的数据表现出矛盾之处:标的资产的价格服从正态分布与实际市场的标的资产呈现尖峰厚尾且倾斜的现象不符。在实际金融市场中,由于非系统风险的存在,股价等金融资产价格会发生不平常的跳跃,即在某些时刻出现了资产价格严重偏离原来价格的现象,资产回报的实证研究发现跳是金融资产价格的基本组成部分。这些“跳跃”可能是由于金融市场中的一些异常情况引起的,如2008年全球金融危机。股票价格的异常波动是由于有关股票的重要新信息的到来,重要的信息只能在离散的时间点到达,而泊松分布的“事件”可以用来刻画股票重要信息的到达,并且假设到达量是独立的,且有相同分布的。因此不少学者考虑用Poisson过程和布朗运动共同驱动的随机微分方程来描述股票价格的变化。这些模型的跳跃幅度可能服从不同的分布,如均匀分布、正态分布、指数分布等。而Merton跳跃模型是跳跃扩散过程中一类被广泛使用的模型。1976年Merton [12] 提出了一个具有泊松跳跃的跳跃扩散过程来匹配股票价格的异常波动,即把股票价格的演化过程用Brown运动和Poisson过程来共同刻画——Merton模型,得到了更一般的期权定价公式。从而引出了用正态分布来刻画跳跃幅度的Merton跳跃,在Merton跳跃中,跳跃幅度和跳跃强度是相互独立的,跳跃幅度服从的是正态分布,跳跃幅度用泊松过程刻画,因此Merton跳跃是一个复合泊松过程。随之,Merton跳跃过程在实际应用建模中起着重要的作用。Mikosch [13] 将Merton跳跃用到保险索赔当中,这样由Merton跳跃过程得到的索赔量模型成为精算师的有力工具。Kou [14] 、Cont和Tankov [15] 也考虑了更大背景下跳跃扩散环境下的期权定价问题。同时,由于金融市场既有跳跃现象,又具有长期相关性和自相似性,因此一些学者研究了带跳分数布朗运动下的期权定价问题,如Sattayatham P. [16] 考虑了在带泊松跳的分数布朗运动下,欧式期权的定价公式。同时对于带跳分数布朗运动下的期权定价公式,往往不直接求解Black-Scholes方程,而是采用保险精算方法或鞅定价理论等方法进行求解。2022年,李飞 [17] 基于风险中性公式和鞅论研究了在模糊环境下基于分数布朗运动的两类幂期权定价问题。2021年,Panhong Cheng和Zhihong Xu [18] 在标的股票价格和公司价值分别遵循带跳跃的混合分数布朗运动的情况下,建立了欧洲脆弱期权定价的新框架,并研究采用精算方法研究欧洲脆弱期权的定价问题,给出了具有跳跃的脆弱期权的封闭式定价公式。
国内外大量研究认为金融资产价格波动是单分形的,即在不同的时间标度下,金融资产价格分布存在着相似性。但是股票价格的变化非常复杂,单分形只能抓住资产价格过程的某一方面特征,仅仅描述资产价格过程变化的一个长期统计行为,并未考虑局部特征,对资产价格动态变化过程的描述不够细致与全面,必然失去许多信息,因此仅用一个分形维数来描述金融资产价格波动序列是不完善的,而多重分形在简单分形基础上增加描述易变性功能,不但能确认资产标度不变性特征,而且能说明金融时序中概率分布的标度变化,更加细致地将经济系统的复杂行为表现出来。1999年,分形理论之父Mandelbrot [19] 在《Scientific American》上指出,多重分形理论在描述金融资产的复杂波动特征上有更强的实用性,运用多重分形理论可以精确地分析出金融资产价格的不同波动。而多重分形过程存在多尺度相关性,也即不仅包括同一尺度不同时刻之间的相关性同时也包括不同尺度之间的相关性,一些学者也通过实证分析验证了多时间尺度因子的存在,多尺度模型可以将年、月、日的时间数据同时输入一个模型中进行参数估计,因此可以显著提高期权定价模型的预测精度。Fouque [20] 提出了多时间尺度随机波动率模型并对期权进行定价研究。此后在多时间尺度随机波动率模型方面的研究进展迅速。Alvarez-Ramirez [21] 运用多仿射法对国际原油价格进行研究,发现存在着与星期和季节有关的两个特征时间标度,并讨论了不同时间标度下相应价格的形成机制。Jeon & Kim等人 [22] 于2021年通过使用偏微分方程方法研究了多尺度条件下脆弱期权的定价问题。何建敏和常松 [23] 运用多重分形游走来分析中国股票市场,验证了中国股票市场的多重分形游走并根据多重分形过程的局部尺度特性和多尺度相关性建立了小波和神经网络相结合的股票价格预测模型,即风险资产价格实际具有多尺度,应运用多个时间尺度去刻画金融资产价格模型。
在以上研究的基础上,本文首先将考虑两种不同时间尺度的数据对标的资产价格的影响,同时将Merton跳跃和多尺度引入到分数布朗运动中,运用带跳多尺度分数布朗运动描述标的资产价格。在此模型基础上,利用无套利原理和风险中性定价原理,得到了欧式期权价格所满足的Black-Scholes偏微分方程;基于鞅定价方法,得到了欧式看涨期权和看跌期权的定价公式以及平价公式。
本文首次将多尺度定价模型与分数跳扩散过程结合起来,既考虑了金融市场的尖峰后尾以及跳跃现象,又考虑了不同尺度的数据对日数据预测的影响,扩展了原有的期权定价模型,给出了理论上的推导分析过程,提升了对期权价格的预测精度。后续将针对此模型进行数值模拟,从而将其运用到金融市场中股票价格的实际预测中,针对期权价格的走势,帮助市场提前采取一些有针对性的风险规避措施,来完善金融市场的管理制度。
2. 预备知识
2.1. 分数布朗运动
定义1 在某概率空间
的随机过程
[24] 如果满足以下条件:
1)
以概率1连续,且
;其样本轨道是连续但几乎不可微的;
2) 是具有平稳增量的连续的零均值高斯过程,且满足
,协方差函数为
;
3)
与
具有相同的有限维分布,即分数布朗运动的增量具有平稳性。
则称
是
上的一个Hurst指数
的分数布朗运动,简记为FBM。
其中Ω表示的是样本空间,即试验中所有可能结果的集合。F表示的是事件集合,是Ω的一些子集构成的集合。P表示的是概率测度,描述在一次随机试验中被包含在F中的所有事件的可能性。
分数布朗运动具有以下性质 [7] :
1) 分数布朗运动的积分表现
分数布朗运动
可表示成随机积分
其中
是Wiener过程,
。
2) 分数Wick-Itô型积分
令函数
,
表示wick积分,S* = {Y:Y为实值随机过程,Ft-适合,可测,且满足
。如果
在
中可积,那么称
为函数Y的分数Wick-Itô型积分。
3) 分数Itô等距性
如果
,则有
;
如果
,定义
。
4) 分数Girsanov定理
设
为概率空间
中的分数布朗运动。设
是一个连续函数,并且
,K是一个函数,
并且满足
定义一个由
生成的新的概率测度
满足
则在新的概率测度
下
是一个分数布朗运动。
5) 分数Ito公式
如果
,并且
,
,
表示所有可测过程
的集合,使得
,那么
将分数布朗运动的Ito法则与标准布朗运动的Ito法则比较可知,原先Ito法则中
项的系数
被
代替了。
2.2. 分数阶几何布朗运动
定义2 对任意的
,如果定义在概率空间
上的随机过程S满足:
其中,
是一个Hurst参数为H的分数布朗运动,且二者相互独立。则称S为分数阶几何布朗运动。
此模型的假设为:1) 市场不存在套利机会;2) 标的资产可以自由地买进或卖出,而且在期权到期之前,对标的资产不支付红利、股息或进行其他形式的分配(市场是无摩擦的);3) 无风险利率r是常数;4) 投资者可以自由借入或贷出资金,借入利率与贷出的利率相等,均为无风险利率,并且是连续复利;而且,所有证券交易可以无限制细分,即投资者可以购买任意数量的标的资产。
从定义可知带有漂移项的几何混合分数布朗运动是标的资产的对数扩散过程由分数布朗运动以及漂移项的线性组合。利用分数Ito公式,可得分数阶几何布朗运动过程的对数形式可重新表达为:
其中
是需要利用离散的数据进行估计的常数。其期望为
,方差为
。
从而有
即得到标的资产
所满足的随机微分方程。
在概率论中,由对数正态分布理论知:如果
,那么
得到分数阶几何布朗运动的期望和方差如下:
2.3. 跳跃过程
泊松过程是一类时间连续、状态离散的随机过程。在实际问题的应用中,一般用泊松过程研究一定时间间隔内某随机事件出现的统计规律。其主要有如下两种定义:
定义3 如果计数过程
满足下列条件 [25] :
1)
;
2) 具有平稳性独立增量;
3)
;
4)
;
5) 对于充分小的
,
,即对于充分小的时间间隔内,最多有一个事件发生,不能有两个或者两个以上事件同时发生。
则称
为强度为λ的泊松过程。
上面是泊松过程的微分定义形式。在此考虑一个微小的时间段dt,结合(3)和(4),可得
如果时间段dt足够小,就可以认为上式等号是成立的。对于泊松过程有时也用如下等价定义:
定义4如果取计数过程
满足下列条件 [26] :
1)
;
2) 具有平稳性独立增量;
3) 对于任意
,
服从参数为
的泊松分布,即
则称
为强度为λ的泊松过程。
金融市场中一般用泊松过程
来表示突发事件发生的次数,用一个随机变量
来表示每次事件发生时带来的影响。若考虑总体影响,则有
,这一新的随机过程就是复合泊松过程。
定义5 [26] 令
是一列独立同分布的随机变量序列,
是强度为
的泊松过程,
两两独立,并且也独立于
。令
,则称
为复合泊松过程。
复合泊松过程的两个性质:
1)
是一个独立增量过程;
2)
的特征函数为
,其中
是随机变量Y的特征函数。
如果复合泊松过程中的跳跃幅度
服从的是正态分布,则被称为Merton跳跃。其具体定义如下所示:
定义6 (Merton跳跃) Merton模型 [12] 假设标的资产价格的变化路径服从跳跃扩散过程。即标的资产价格路径分为连续部分与跳跃部分。连续部分用几何布朗运动描述,间断部分用泊松跳跃过程描述,即Merton模型假设标的资产价格的变化模式为:
其中α为股票的瞬时期望收益,σ为跳跃不发生时股票的瞬时波动率,
为标准布朗运动,
表示影响股票价格突发事件发生的次数,服从强度为
的泊松分布,
是描述
发生跳跃的点过程,若
,标的资产价格产生跳跃现象;若
,则标的资产价格没有伴随跳跃。在区间
内,风险资产发生跳跃的概率为
,
表示单位时间内重大信息到来的平均个数。泊松过程
与跳幅
以及布朗运动
是相互独立的。
表示的是股票价格的相对跳跃高度,是一个独立的同分布序列,也是随机变量,且满足以下性质:
即
服从的是对数正态分布。其概率密度函数为:
由特征函数公式,可得
的均值为
,方差为
。
Merton模型中的跳跃部分后来也被称为Merton跳跃。本文标的资产所满足的随机微分方程中,跳跃部分就是Merton跳跃。
同时可以得到,在风险中性的假设条件下,看涨期权的价值等于未来预期价值按照无风险利率折现之后的现值,即:
按照跳跃的次数以及所有可能的扩散路径对
进行分组,可以得到所有
的值,因此有:
其中,
为经历n次跳跃及其后的扩散过程之后,标的资产价格在到期日的对数正态分布。
2.4. 多尺度
在实际金融市场中,股票的价格受多周期价格因素的影响。金融时间序列分析大多数情况下处理离散时间序列,根据数据的采样频率不同,金融时间序列具有多尺度空间特性。常用的采样频率从高频到低频如表1所示。

Table 1. Commonly used time scales for financial time series
表1. 金融时间序列常用的时间尺度
金融时间序列常用的时间尺度见表1。除了TS0是非规则时间序列,其他所有时间尺度都符合规则时间尺度。相邻时间尺度的缩放比例为:
除了TS0,在每一个时间尺度TSi,原始时间序列数据可以被分为规则的时间序列,时间间隔为相应的时间尺度。例如,TS5是小时数据,每一个时间间隔是一小时,一小时内所有成交的数据被视为一个数据点。
现假设两个不同周期(尺度)的股票价格分别满足两个不同Hurst指数的分数阶布朗运动:
其中,
表示观测的时间点,
表示的是时间尺度为
的标的资产在各个时间点得到的观察数据,
表示的是时间尺度为
的标的资产在各个时间点得到的观察数据。其中
定价模型中的分数布朗是Hurst指数为
的分数布朗运动,
定价模型中的分数布朗是Hurst指数为
的分数布朗运动。例如若
的时间尺度是日,
的时间尺度是周,这时可以令
。
由分数阶布朗运动的自相似性可知:
为简化计算,本文假设股票价格满足以下多尺度公式:
为了描述多尺度分数布朗运动的叠加性质,本章对期权的对数价格运用蒙特卡洛方法进行数值模拟。
所得图形如下所示。
多尺度分数布朗运动的模拟图见图1。其中
表示的是时间尺度为
的分数布朗运动的对数,
表示的是时间尺度为
的分数布朗运动的对数,S则是这两个不同尺度对数分数布朗运动的叠加。

Figure 1. Multi-scale fractional Brownian motion simulation diagram
图1. 多尺度分数布朗运动模拟图
3. 风险资产价格模型及欧式期权定价
3.1. 风险资产价格模型
考虑一个股票价格既有连续又有间断的金融市场,对于连续部分有“尖峰厚尾”和“长期相关性”的特性,对于间断部分在价格过程中有异常波动。本文将跳引入到分数布朗运动中,考虑不同时间尺度的收益率数据,对日价格预测的影响。因此在建立模型时,考虑两种不同H指数、不同时间尺度的带跳分数布朗运动,选用多尺度时间序列模型进行预测。
为了简化模型的推导过程,本文做出如下假设:
1) 证券交易可卖空获得全部收入;
2) 市场上不存在无风险套利机会;
3) 标的资产可以自由地买进或卖出,而且在期权到期之前,对标的资产不支付红利、股息或进行其他形式的分配(市场是无摩擦的);
4) 无风险利率r为常数,并对所有期限都是相同的,选取银行的存款利率为无风险利率;
5) 期权的波动源于股票价格变化的不定性;
6) 标的资产遵循的是下面式(1)给出的方程;
7) 投资者可以自由借入或贷出资金,借入利率与贷出的利率相等,均为无风险利率,并且是连续复利;而且,所有股票交易可以无限制细分,即投资者可以购险利率,并且是连续复利;而且,所有证券交易可以无限制细分,即投资者可以购买任意数量的标的资产。
基于以上五点假设,本文采用带跳多尺度分数布朗运动,刻画金融资产价格的变化过程。此时,投资于金融市场的风险资产价格
满足:
(1)
如图为参数
时的风险资产价格的模拟图。
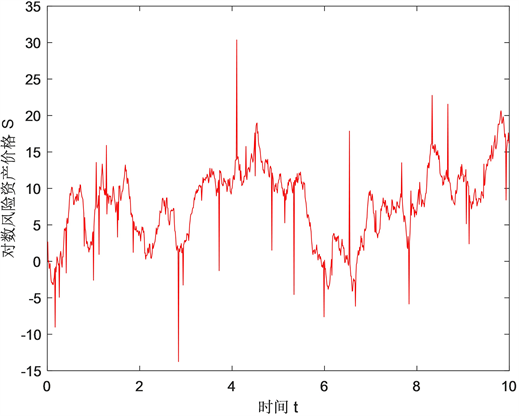
Figure 2. Simulation of logarithmic risk asset prices
图2. 对数风险资产价格模拟图
表示的是风险资产取对数后的数值模拟图见图2。可以看出,图中出现了某些时刻资产价格严重偏离原来价格的现象,这说明在某些时刻股票价格出现了幅度比较大的跳跃。
对于式(1),其中的积分表示wick型积分,μ表示预期收益率。
分别是两种不同分数布朗运动所对应的波动率系数,
都是常数。
分别是Hurst指数为
的分数布朗运动对应的时间尺度。
表示影响股票价格突发事件发生的次数,服从强度为
的泊松分布。在区间
内,风险资产发生跳跃的概率为
。
的定义与Merton跳跃中的定义一样。泊松过程
与跳幅
以及Hurst指数为
的分数布朗运动
是相互独立的。同时由于泊松过程在一个充分小的区间里最多只有一次跳跃发生,因此当
时,
,
。
在此假设下,可以得到风险资产
的表达式:
定理1若风险资产价格满足随机微分方程(1),则其表达式为:
(2)
证明:假设股票价格
在随机时间
处发生跳跃 [27] ,对应的相对跳跃高度即跳幅分别为
,在相邻2次跳
之间
没有发生跳跃,因此遵循多尺度分数B-S模型,跳跃时间
服从参数为λ的Poisson过程,因此在
上
没有发生跳跃,有
(3)
在时刻
处发生了一次跳跃,跳跃
,则
。
对任意
,求解随机微分方程(3),由分数布朗运动的Wick-Itô积分公式 [28] 以及自相似性有:
因此
当
时有
由
,得
有
因此当
时有
又
,因此
重复上述迭代过程,并考虑股票价格在
内没有发生跳跃的情况即可得
因此得到风险资产价格
的表达式。
3.2. 带跳多尺度分数布朗运动的伊藤公式
定理2假定
,
,
表示的是
上关于t一阶连续可导,关于x二阶连续可导函数的全体。且
,
,
,均属于
,则多尺度分数跳扩散过程的伊藤公式为:
(4)
证明:设
在
时刻发生第i次跳跃,当
时,即
在
时刻内只发生了一次跳跃,且跳跃时刻为
,则在
和
内没有发生跳,由分数型伊藤公式可得:
由于在
时刻发生了跳跃,因此
,所以
在
时刻的变化为
,因此
从而当
内发生的跳跃次数服从泊松过程时,有
定理得证。
3.3. 带跳多尺度分数阶Black-Scholes方程
定理3在式(1)定义的带跳多尺度分数阶布朗运动模型下,考虑分数布朗运动的长记忆性,取Hurst指数
,到期时间为T,执行价格为K的欧式看涨和看跌期权,假设期权的价格为V,那其在时刻
与标的资产价格
和时间t有关,应该被记为
,其满足如下的偏微分方程:
其中,考虑一个带有到期日T和执行价格
的欧式看涨期权。如果
,合同毫无意义,因此合同购买者不执行期权。如果
,合同购买者有权利以敲定价格K购买一份股票。接着以市场价格立马卖出,因而购买者能获利
。总之,在时刻T,合同持有者能得到现金流为
。而对于到期日T和执行价格
的欧式看跌期权。如果
,合同毫无意义,因此合同购买者不执行期权。如果
,合同购买者有权利以敲定价格K购买一份股票。接着以市场价格立马卖出,因而购买者能获利
。总之,在时刻T,合同持有者能得到现金流为
,同时欧式期权只能在到期日进行交易。因此,其边界条件为:
证明:基于∆-对冲原理 [29] ,在t时刻构造投资组合
,
的构造如下所示。
空头:∆t份股票(St);多头:1份欧式期权(Vt)。因此形成投资组合
根据无套利定价原理,无套利定价(no-arbitrage pricing principle)作为在金融市场上常见的定价方法,其原理在于金融市场上的套利行为是十分短暂的,因为一旦有套利的可能性时,投资者会很快实施套利从而使得市场重新回到无法套利的均衡中。因此,某种金融产品在市场的合理价格就应当是当它在无套利机会时的价格。即市场不存在套利机会,投资组合在
的任意时间,按无风险利率r贴现的价格是相等的。因此选取适当的∆,使得在
时段内,
是无风险的。
设在时刻t形成投资组合
,并在时段
内,不改变份额∆。由于
是无风险的,因此在时刻
,投资组合的回报是
即
(5)
由于
是由随机微分方程(2)确定的随机过程,因此由定理1和式(4)可得:
表示的是由于发生了跳跃幅度为
的跳跃,标的资产价格从
变成了
,引起期权价格变化的微分。
将其代入方程(5)可得:
整理后得:
(6)
由于股票价格的期望相对变化值为
(7)
其中
是强度为λ的泊松过程,
,所以
,因此
(8)
另一方面由于等式右端是无风险的,即期权价格的变化与随机项无关,因此等式左端随机项
前面的系数必须为0,即选取
(9)
将(7~9)代入方程(6),并消除
项后可得:
这就是刻画期权价格变化的分数阶Black-Scholes方程。
推论1 若当跳跃强度
,即无跳跃时,可以验证Black-Scholes方程化简为
这就是多尺度分数布朗运动的Black-Scholes方程。
3.4. 欧式看涨与看跌期权定价公式
由于带跳分数阶B-S方程的解难以直接得到,因此本文从概率论的角度推导期权定价公式。
令
是一个概率空间,
是一个分数Brown运动,它跟测度P有关。记
是一个拟条件期望,也跟测度P有关,给出下列引理。
引理1 [7] 令
,考虑下面的过程
由分数布朗运动的Girsanov定理 [21] ,存在一个新的测度
,使得
同样是分数布朗运动。可记
是测度
下的一个拟条件期望,令
引理2 [30] (多尺度分数风险中性定价公式)任意域流
的可测未定权益F在任意时刻
时刻的价格为
其中
指的是
在概率测度P下的拟条件期望,r表示的是常数无风险利率。
引理3 [31] 若函数f满足
,那么对任意的
,可以有
引理4 [31] 若函数f满足
,对每个
,以及
有:
引理5 [30] (鞅理论)令
是一个概率空间,F是σ-代数上的域流,F是F上的子域流,
是适应于F的随机过程,如果对任意的
,随机过程满足下式
那么把随机过程
叫做一个鞅。
引理6 [30] (风险中性定价方法)在概率测度Q下,风险资产S在
时刻的期望回报率与无风险证券的回报率相同,将具有这种性质的市场称为风险中性世界,这里所有投资者不要求对风险补偿,于是Q称为风险中性测度,或鞅测度,这种定价方法叫做风险中性定价。
在此基础上,本文推导得到如下欧式看涨期权的定价公式。
定理4记n为股票价格在
内发生跳跃的次数,r表示常数无风险利率;
为标准正态分布函数,K为执行价格,T为到期日。假设标的资产价格服从上述带跳多尺度分数布朗运动定价模型,则对任意
,欧式看涨期权的价格为
(10)
其中
证明:终端时刻为T的欧式看涨期权收益为
,由引理2以及风险中性定价方法得,可以找到唯一的等价鞅测度Q,在此测度下市场是风险中性的,使得期权在t时刻的贴现价值为
(11)
其中
表示的是随机变量X的数学期望,
表示的是关于域流
下随机变量X的拟条件期望。
式(11)中的
是一个示性函数,取值为
因为
(12)
所以在
(即标的资产在
内发生跳跃的次数是n)时,可得:
由
可得:
令
,
则
。
对引理4,取
,即得:
又因为
表示的是股票价格的相对跳跃高度,是一个独立的同分布序列,也是随机变量,并满足下列性质:
是一个独立同分布的随机变量,因此
是一个独立同分布的复合泊松过程,其服从均值为nm,方差为
的正态分布。
综上所述可得
的求解过程如下:
做变量替换,令
,
则原式转化为
因此得
其中期望
,方差
.
下面考虑
的求解。
令
则
则
又
,
,
是一个独立同分布的随机变量,所以
。
由引理1以及引理6的风险中性定价方法,现在考虑如下过程
,
,由分数布朗运动的Girsanov定理 [21] ,存在一个测度R与测度Q等价且是风险中性的,使得
在R下是一个分数布朗运动(记为
)。同时由测度变换论可知,
在新的测度R下也发生了变化,令
,则
在R下仍是一个复合泊松过程。
另一方面由引理3,
(13)
又
又
满足式(12),因此若令
那么
其中
代入式(13)可得:
所以代入
的表达式中可得:
求得
的解析式后,代入式(11),可得欧式看涨期权的期权定价公式如下所示:
按照上述证明思路类似可得以下结论。
推论2设执行价格为K,到期日为T,标的资产价格服从上述风险资产价格公式,则对任意
,欧式看跌期权
的价格为
由如上看涨期权价格和看跌期权价格公式,可得以下平价公式。
推论3 (平价公式)设执行价格为K,到期日为T的欧式期权平价公式为:
表示欧式看涨期权在t时刻的价格,
表示欧式看跌期权在t时刻的价格。
推论4当跳跃强度
,即无跳跃时,可以验证平价公式化简为
一般情况下,可以认为
.此时上式简化为经典的欧式期权平价公式
4. 数值模拟
4.1. 标的资产价格的数值模拟
为了显示跳跃对标的资产价格的影响,本文将含跳和不含跳的两组曲线放在同一个图形中进行对比。同时将跳跃强度不同的两组图形,放在图窗中进行对比分析。其中两幅图共同参数设置为
。第一幅图的跳跃强度为
,第二幅图的跳跃强度为
。
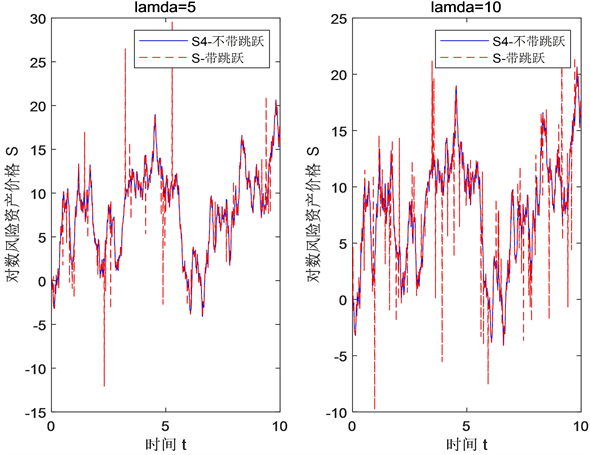
Figure 3. Comparison of different jump intensities
图3. 不同跳跃强度对比图
图3是标的资产价格服从不同跳跃强度的带跳分数布朗运动的对比图。从图中可以,由于跳跃参数的设置,在一些时刻标的资产价格会突然发生大幅度的跳跃,跳跃的均值与方差越大,标的资产价格偏离原来轨道的幅度就会越大。在其他参数相同的情况下同时对比第一幅图形和第二幅图形可以看出,跳跃强度越大,跳跃发生的时刻就越多,整个图形中一些异常波动的数值点就越明显。这也与实际金融市场中,异常情况发生的次数越多,则期权市场价格波动的越明显,对期权价格预测的掌控难度越大的事实相吻合。
4.2. 期权价格的数值模拟
上文给出了在标的资产价格服从带跳多尺度分数布朗运动过程下,欧式看涨与看跌期权的定价公式,以及平价关系。本节以带跳多尺度分数模型下的欧式期权为例,通过数值模拟讨论Hurst指数
,跳跃强度λ和到期时间T不同对期权价格的影响。
设置模型中的相应参数如下:
。Hurst指数
,跳跃强度λ和到期时间T以及期权价格如表2所示。

Table 2. Numerical simulation results of European call and put options under multi-scale fractional Brownian movement with jump
表2. 带跳多尺度分数布朗运动下欧式看涨、看跌期权的数值模拟结果
带跳多尺度分数布朗运动过程下,欧式看涨、看跌期权的价格的数值模拟结果见表2,计算结果表明:
1) 在参数给定的条件下,带跳多尺度分数布朗运动过程下,欧式看涨的价格要高于欧式看跌期权的价格,价格高出的部分可由推论3的期权平价公式来给出合理解释,即看涨期权价格高出看跌期权价格的部分为
2) 在其他参数不变的情况下,欧式看涨、看跌期权的价格随着Hurst指数
的增加而减小,这表明欧式看涨、看跌期权价格是Hurst指数
的减函数。同时这也说明不同时间尺度的数据,对期权价格的总体影响是相似的,Hurst指数越大表明期权价格变化增量之间的相关性越强,长相依性越强,且是正相关,因此期权价格就会减小。
3) 其余参数不变的情况下,欧式看涨、看跌期权的价格随着到期时间T减少而减少。这是因为期权作为一种合约,是有时间价格的,随着期权剩余时间的减少,期权价格也减少。
4) 给定其余参数的条件下,随着标的资产价格的跳跃强度λ减小,看涨期权的价格减小,看跌期权的价格增加。这是因为:一方面,随着标的资产的跳跃强度λ增大,标的资产的波动就增加,因此看涨期权的价格在减小,看跌期权的价格在增加。另一方面,当Hurst指数
时,标的资产价格具有持久性,表现为:若前一阶段股价走高,则下一阶段也走高,反之亦然。当标的资产价格由于持久性持续升高时,看涨期权的价格升高,看跌期权的价格反而降低。
5. 结论
欧式期权是金融市场上一类非常重要的金融衍生产品,也是目前我国金融市场上流行的主要金融衍生产品,因此对其进行准确地定价具有非常重要的金融意义。本文拓展了传统的期权定价模型,分别引入Merton跳跃、分数阶几何布朗运动以及多尺度理论,推导了在此模型下的伊藤公式,并利用无套利原理和风险中性原理,推导了在欧式期权,在到期前任意时刻t的分数阶Black-Scholes方程。随后基于分数布朗运动的Girsanov定理,建立了带跳多尺度分数布朗运动下风险中性的等价鞅测度,从而运用鞅定价方法,推导得到欧式看涨期权与看跌期权的定价公式以及平价公式。同时数值模拟的结果显示,跳跃参数的设置会引起标的价格突然发生突变,跳跃强度越大,跳跃发生的时刻就越多,标的资产价格模拟图形中,一些异常波动的数值点就越明显。在其他参数不变的情况下,欧式看涨、看跌期权的价格随着Hurst指数
的增加而减小,成反比关系;随着到期时间T减少而减少。看涨期权价格与跳跃强度λ成正比,看跌期权价格与跳跃强度λ成反比。
在本文所建立的带跳多尺度分数模型基础上,还有如下问题可以进行后续研究。1) 本文考虑的Merton跳扩散过程具有一定的特殊性,可以考虑其他更一般的跳跃过程,如Levy跳跃。2) 同时本文考虑股票价格的多尺度性时,只考虑了两个尺度,在后续的研究中也可以将多个时间尺度同时考虑进去。3) 本文的参数也只考虑常数的情形,没有考虑到参数时变性的情况,可以将其扩展到随机环境或函数。4) 本文考虑的是在此模型下欧式期权的定价问题,可以将此模型推广到其他期权的定价问题上,如亚式期权,障碍期权等。
基金项目
国家自然科学基金面上项目(12071215)。
文章引用
胡 静,黄小涛. 带跳多尺度分数布朗运动下欧式期权定价问题
European Option Pricing Problem Involving Multi-Scale Fractional Brownian Motion with Jump[J]. 理论数学, 2023, 13(09): 2536-2559. https://doi.org/10.12677/PM.2023.139259
参考文献
- 1. Black, F. and Scholes, M. (1973) The Pricing of Options and Corporate Liabilities. Journal of Political Economy, 81, 637-654. https://doi.org/10.1086/260062
- 2. Kolmogorov, A. (1940) Wienersche spiralen und einige andere interessante Kurven in Hibertschen Raum. The Academy of Sciences of the U.S.S.R., 26, 115-118.
- 3. Mandelbrot, B.B. and Van Ness, J.W. (1968) Fractional Brownian Motions, Fractional Noises and Applications. SIAM Review, 10, 422-437. https://doi.org/10.1137/1010093
- 4. Lin, S.J. (1995) Stochastic Analysis of Fractional Brownian Motion, Fractional Noises and Applications. SIAM Review, 10, 422-437. https://doi.org/10.1137/1010093
- 5. Duncan, T., Hu, Y. and Pasik-Duncan, B. (2000) Stochastic Calculus for Fractional Brownian Motion I: Theory. SIAM Journal on Control and Optimization, 38, 582-612. https://doi.org/10.1137/S036301299834171X
- 6. Hu, Y. and Oksendal, B. (2003) Fractional White Noise Calculus and Applications to Finance. Infinite Dimensional Analysis, Quantum Probability and Related Topics, 6, 1-32. https://doi.org/10.1142/S0219025703001110
- 7. Necula, C. (2002) Option Pricing in a Fractional Brownian Motion Environment. Mathematical Reports, 2, 259-273.
- 8. 程潘红. 分数布朗运动环境下上证50ETF期权定价的实证研究[J]. 经济数学, 2019, 36(3): 9-15.
- 9. Ahmadian, D. and Ballestra, L.V. (2020) Pricing Geometric Asian Rainbow Options under the Mixed Fractional Brownian Motion. Physic A: Statistical Mechanics and Its Applications, 555, Article ID: 124458.
https://doi.org/10.1016/j.physa.2020.124458
- 10. 王体标. 几何分数布朗运动下的商品互换期权定价公式[J]. 应用数学, 2006(S1): 193-195.
- 11. 侯营营. 分数布朗运动环境中欧式新型期权的定价[D]: [硕士学位论文]. 沈阳: 东北大学, 2013.
- 12. Merton, R. (1976) Option Pricing When Underlying Stock Returns Are Discontinuous. Journal of Financial Economics, 3, 125-144. https://doi.org/10.1016/0304-405X(76)90022-2
- 13. Mikosch, T. (2009) Non-Life Insurance Mathematics. Springer, Berlin. https://doi.org/10.1007/978-3-540-88233-6
- 14. Kou, S.G. (2002) A Jump-Diffusion Model for Option Pricing. Management Science, 48, 1086-1101.
https://doi.org/10.1287/mnsc.48.8.1086.166
- 15. Cont, R. and Tankov, P. (2004) Non-Parametric Calibration of Jump-Diffusion Option Pricing Models. Journal of Computational Finance, 7, 1-49. https://doi.org/10.21314/JCF.2004.123
- 16. Sattayatham, P., Intarasit, A. and Chaiyasena, A.P. (2007) A Frac-tional Black-Scholes Model with Jump. Vietnam Journal of Mathematics, 35, 1-15.
- 17. 李飞. 模糊环境下基于分数布朗运动的两类幂期权定价研究[D]: [硕士学位论文]. 成都: 西南财经大学, 2022.
- 18. Cheng, P.H. and Xu, Z.H. (2021) Pricing Vulnerable Options in a Mixed Fractional Brownian Motion with Jumps. Discrete Dynamics in Nature and Society, 2021, Article ID: 4875909. https://doi.org/10.1155/2021/4875909
- 19. Mandelbrot, B.B., Fisher, A.J. and Calvet, L.E. (1998) A Multifractal Model of Asset Returns. Social Science Electronic Publishing.
- 20. Fouque, J.P., Papanicolaou, G. and Sircar, R. (2003) Multiscale Stochastic Volatility Asymptotics. SIAM Journal on Multiscale Modeling and Simulation, 2, 22-42. https://doi.org/10.1137/030600291
- 21. Alvarez-Ramirez, J., Escarela-Perez, R., Espinosa-Perez, G. and Urrea, R. (2009) Dynamics of Electricity Market Correlations. Physica A: Statistical Me-chanics and Its Applications, 388, 2173-2188.
https://doi.org/10.1016/j.physa.2009.02.014
- 22. Jeon, J., Kim, G. and Huh, J. (2021) An Asymptotic Expansion Approach to the Valuation of Vulnerable Options under a Multiscale Stochastic Volatility Model. Chaos, Solitons and Fractals, 144, Article ID: 110641.
https://doi.org/10.1016/j.chaos.2020.110641
- 23. 何建敏, 常松. 中国股票市场多重分形游走及其预测[J]. 中国管理科学, 2002, 10(3): 11-17.
- 24. Lin, Y.L., Wu, C.B. and Kang, B.D. (2003) Optimal Models with Maximizing Probability of First Achieving Target Value in the Preceding Stages. Science in China, 46, 396-414.
- 25. Tankov, P. (2003) Financial Modelling with Jump Processes. Chapman and Hall/CRC, Boca Raton.
https://doi.org/10.1201/9780203485217
- 26. 黄文礼. 基于分数布朗运动模型的金融衍生品定价[D]: [博士学位论文]. 杭州: 浙江大学, 2011.
- 27. Xu, W.D., Xu, W.J., Li, H.Y. and Xiao, W.L. (2012) A Jump-Diffusion Ap-proach to Modelling Vulnerable Option Pricing. Finance Research Letters, 9, 48-56. https://doi.org/10.1016/j.frl.2011.07.001
- 28. Bjork, T. and Hult, H. (2005) A Note on Wick Products and the Fractional Black Scholes Model. Finance and Stochastics, 9, 197-209. https://doi.org/10.1007/s00780-004-0144-5
- 29. 姜礼尚. 期权定价的数学模型和方法[M]. 北京: 高等教育出版社, 2003.
- 30. Ciprian, N. (2002) Option Pricing in a Fractional Brownian Motion Environment. Working Paper of the Academy of Economic Studies, 6, 8079-8089.
- 31. Shokrollahi, F. and Klcman, A. (2014) Pricing Currency Op-tion in a Mixed Fractional Brownian Motion with Jumps Environment. Mathematical Problems in Engineering, 2014, Article ID: 852810. https://doi.org/10.1155/2014/858210









