Operations Research and Fuzziology
Vol.
10
No.
03
(
2020
), Article ID:
37178
,
10
pages
10.12677/ORF.2020.103025
Performance Analysis of M/M/1/N Queue System with Delayed Startup Time and Partial Failure
Huijun Lu, Yang Song
College of Science, Nanjing University of Aeronautics and Astronautics, Nanjing Jiangsu
Received: Aug. 3rd, 2020; accepted: Aug. 14th, 2020; published: Aug. 21st, 2020

ABSTRACT
This paper focuses on an M/M/1/N queuing system with delayed startup time and partial failure. In such a queuing system, the server needs to experience a random time of start-up from the shutdown period to the normal working period which follows an exponential distribution. Partial failure is not to immediately stop service for repair. It means that the system no longer admits any customer from outside, while it conducts service for the existing customers in the system with a lower rate. After all customers finishing the service and leaving, the system enters into the repair period immediately. By analyzing the two dimensional continuous-time Markov chain in this paper, the Quasi Birth and Death (QBD) process for the system is established. By using the censoring technique, the stable distribution of the system is obtained according to the matrix geometric solution method. Therefore, the sensitivity of the system to parameters is further analyzed by assigning different values to the single parameter.
Keywords:M/M/1/N, Delayed Startup Time, Partial Failure, Censoring Technique, Matrix-Geometric Solution

带有延迟启动时间和部分故障的M/M/1/N排队系统的性能分析
卢会军,宋旸
南京航空航天大学理学院,江苏 南京
收稿日期:2020年8月3日;录用日期:2020年8月14日;发布日期:2020年8月21日

摘 要
本文研究的是一个带有延迟启动时间和部分故障的M/M/1/N排队系统。在此排队系统中,服务台从关闭期到正常工作期间,需要经过一段随机时长服从指数分布的启动期。本文中所研究的部分故障指的是,系统发生故障后并不会立即停止服务,而是以一个较低的速率服务系统中现存的顾客,同时拒绝新到达的顾客进入系统中,当所有现存顾客服务完成并离开后系统立即进入修复期。易知本文中的二维连续马尔可夫过程为拟生灭过程(QBD),利用删失技巧及矩阵分析方法便可得到该系统的平稳分布,如此,赋予各参数不同的值,便可进一步分析系统对各参数的敏感度。
关键词 :M/M/1/N,延迟启动时间,部分故障,删失技巧,矩阵分析方法

Copyright © 2020 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
排队论是对排队等候过程中出现的拥挤和延误进行的数学研究,其研究内容涉及建模、性能、控制、仿真、计算、推理和优化等各个方面。排队论研究等待服务的每一个组成部分,包括到达过程、服务过程、服务台数量、等待空间的容量、排队规则和顾客数量(可能是人、数据包、汽车等)。
丹麦数学家Erlang [1] 在一个世纪以前第一次在他的论文中介绍了排队论,用来研究电话通话问题,从此开创了这门应用数学学科。Gnedenko和Kovalenko [2] 讨论了带有部分故障的排队系统并且研究了部分故障在M/G/1系统中的影响。部分故障意味着系统在正常工作期间的任意时间点都可能会发生故障,但是,当系统发生故障时,服务不会立即完全停止,而是继续以一个较低的速率继续工作,并且不再接受其他外来的顾客。Avi-Itzhak和Naor [3] 在他们的论文中关注的是两种带有故障的排队模型,其中一个模型是故障只会发生在服务台正在进行服务时,另外一个模型是故障可能会发生在系统空闲时。White和Christie [4] 在他们的论文中研究的是带有故障和带有优先权的排队系统的相似性,并且讨论了这两种效果。Sridharan和Jayashree [5] 研究的是具有一般故障、部分故障和完全故障的有限队列的一些特性,此处的部分故障是服务器发生故障时,允许顾客进入系统。Wang等人 [6] 研究的是带有部分故障的马尔可夫单服务台队列的均衡问题。Economou和Kanta [7] 研究的却是具有开关周期交替的马尔可夫单服务台排队系统。文章 [8] [9] [10] 考虑的都是具有工作故障的不同的排队模型。Xu等人 [11] 分析的是M/M/1排队系统中顾客的均衡策略行为,该排队系统是带有部分故障和可修复的条件。文章 [12] [13] [14] 讨论的都是带有延迟启动的排队系统。延迟启动的排队系统指的是,系统从关闭期到正常工作需要经过一段时间的启动期才能开始正常服务。杨喜娟等人 [15] 研究的是带有启动时间和工作故障的M/M/1/N排队系统。
基于上述学者的研究,本文考虑的是带有延迟启动时间和部分故障M/M/1/N排队系统的性能。QBD的特点和矩阵分析方法在解决二维马尔可夫过程中有非常重要的应用,相关问题在论文 [16] [17] [18] [19] 中有提及到。删失技巧在有限空间队列和无穷空间队列的排队模型中起着重要的作用,它可以使得计算更加的简便。
本文的排队系统可以模拟生活中的一些问题。假设有一台正常工作的机器在某一时刻发生了故障,它会立即被一台工作速率更低的备用机器所代替,以保障持续的工作。在这种情况下,备用机器仅完成系统内未完成的任务,当所有现存任务完成后,发生故障的机器才会被送去修理。
本文的组织结构如下:第2节描述了本文的模型;第3节中运用删失技巧和矩阵分析方法,得到了排队系统的平稳分布;第4节给出了一些数值算例;第5节总结。
2. 模型描述
本文考虑的是一个带有延迟启动时间和部分故障的M/M/1/N排队模型,其模型描述如下:
1) 系统中只有一个服务台,服务台每次只能服务一个顾客,队列最大容量为N。
2) 顾客的到达是一个泊松过程,参数为 。
3) 当服务台正常服务完系统中所有的顾客后,立即进入一段随机长度为L的休眠期,L服从参数为 的指数分布。若休眠期结束时,队列中有顾客,则服务台立即进入正常忙期,正常忙期内顾客的服务时长服从参数为 的指数分布。否则,队列为空,系统立即进入关闭期。
4) 若服务台在正常工作过程中发生故障,则系统不再接受新到达的顾客,并且服务台将以较低的速率 进行服务,直到系统为空,此时系统立即进入修复期进行维修。维修完成后系统进入休眠期。假设系统发生故障的过程服从参数为 的泊松过程,维修时长服从参数为 的指数分布。
5) 在系统关闭期内,若有外部顾客到达,则关闭期结束,经过一段随机长度为T的启动期,系统进入正常忙期,T是服从参数为s的指数分布。
6) 上述的随机过程都是相互独立的,且在本文中规定 ,以保证系统最终是平稳的。服务台的服务遵循先到先服务(FCFS)原则。
3. 系统的平稳分布
令 表示t时刻系统队列中的顾客数, 表示t时刻系统的状态。根据第2节的模型描述,有:
由此可知, 是一个二维连续时间马尔可夫过程,状态空间为
。
特别地, 表示的是系统关闭期; 表示的是系统休眠期; 表示系统维修期; 表示系统当前状态为j,同时系统中有k个顾客。系统的状态转移图如图1所示。从图1中,可以看到上述二维连续时间马尔可夫过程是不可约的,根据 [20] 文中的定理6.2.16和推论6.2.6,可知本文系统的平稳分布是存在且唯一的。
令 ,为系统的平稳分布,则平衡方程如下
, (1)
, (2)
, (3)
, (4)
。 (5)
由归一化条件知
(6)
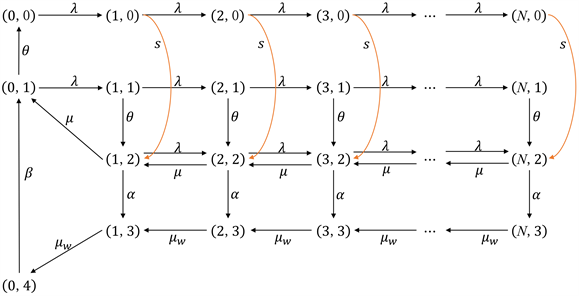
Figure 1. State transition diagram (a)
图1. 状态转移图(a)
根据删失技巧,可以得到删失后的马尔可夫过程的状态转移图,如图2所示,然后通过一些简单的计算,就可以得到本文模型的平稳分布。
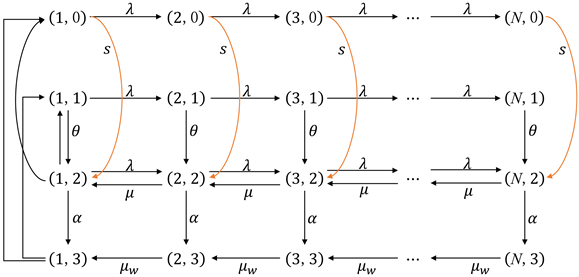
Figure 2. State transition diagram (b)
图2. 状态转移图(b)
删失掉状态 ,,,可知一些状态转移速率变为:
,
,
,
。
下面我们就来研究删失后的马尔可夫过程。
根据图2,易知删失后的马尔可夫过程的Q矩阵为
,
其中
,,,
,,
状态空间为 。
根据上文中的Q矩阵,易知删失后的马尔可夫过程是不可约的,且有唯一的平稳分布。下面我们先给出如下定义:
,,
,,
。
根据删失后的马尔可夫过程的平衡方程,可得
, (7)
, (8)
,, (9)
, (10)
。 (11)
假设
,, (12)
其中 是4阶方阵。如果 和 是非奇异的,则
, (13)
, (14)
其中 ,。
接下来,将(14)代入(10)中,如果 也是非奇异的,可得
, (15)
其中 。
最后,根据(9)和(12),有
,, (16)
其中 。
显然, 可由(12)~(16)推出。根据Elhafs和Molle [16] 文中所述,可知
,,
其中 ,,。在(12)中,令 ,可得
。 (17)
将(13)和(17)代入(8)中,
。 (18)
根据归一化条件
,
得
, (19)
其中e是单位列向量。将(13)代入(19)中,易得
。 (20)
结合(18)和(20), 易知,再由(13)便可得 。接着根据(12),有
,。
由于删失后的马尔可夫过程满足下面的归一化条件
, (21)
由(6)和(21),易知
,。
同时,基于(3)~(5),可以得到下面的等式:
4. 系统性能分析
设 。系统的稳态性能定义如下:
1) 系统吞吐率
。
2) 系统稳态可用度
。
3) 系统稳态队长
。
4) 系统处于正常忙期的概率
。
5) 系统处于故障忙期的概率
。
6) 系统处于修复期的概率
。
7) 系统处于关闭期的概率
。
其次,我们给出了一些数值算例来说明一些参数对系统性能的影响情况。
图3反映的是 对 的影响,当其它参数不变时, 随着 的增大而增大,即系统吞吐量随着到达速率的增大而增大。图4反映的是 对 的影响和 对 的影响,当 不断增大时 先减小到某一数值后不断增大,当 增大时 随之而减小。图5反映的是 和s对 的影响,当 的增大时, 先增大到某一数值后不断减小,而 随着s的增大而增大直到趋于一个固定的值。图6反映的是 对 和 的影响,显然, 和 随着 的增大而减小。图7反映了 对 的影响,其中 随着 的增大而增大。
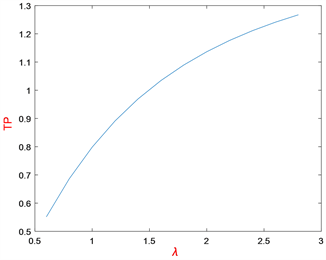
Figure 3. versus for
图3. 当 时, 对 的影响

Figure 4. versus for ; versus for
图4. 当 时, 对 的影响;当 时, 对 的影响
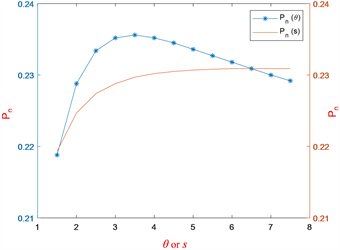
Figure 5. and s versus for and
图5. 当 时, 对 的影响;当 时,s对 的影响
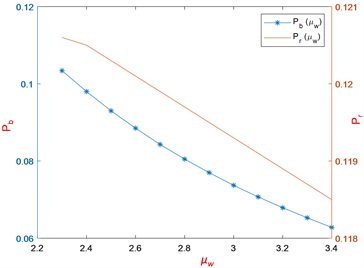
Figure 6. versus and for
图6. 当 时, 对 和 的影响
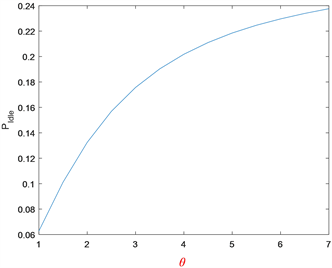
Figure 7. versus for
图7. 当 时, 对 的影响
5. 总结
本文主要研究的是带有延迟启动时间和部分故障的M/M/1/N排队系统的性能,根据删失技巧和矩阵分析方法,得到了该系统的平稳分布然后分析了系统的性能。作为本文的拓展,我们将考虑带有无限等待队列的排队系统,使用同样的技巧,可以研究排队系统的尾部渐近性。
文章引用
卢会军,宋 旸. 带有延迟启动时间和部分故障的M/M/1/N排队系统的性能分析
Performance Analysis of M/M/1/N Queue System with Delayed Startup Time and Partial Failure[J]. 运筹与模糊学, 2020, 10(03): 239-248. https://doi.org/10.12677/ORF.2020.103025
参考文献
- 1. Erlang, A.K. (1909) The Theory of Probabilities and Telephone Conversations. Nyt Tidsskrift for Matematik, 20, 33-39.
- 2. Gnedenko, B.V. and Kovalenko, I.N. (1989) Introduction to Queueing Theory. Birkhauser Boston Incor-porated, Cambridge, MA.
- 3. Avi-Itzhak, B. and Naor, P. (1963) Some Queuing Problems with the Service Station Subject to Breakdown. Operations Research, 11, 303-320. https://doi.org/10.1287/opre.11.3.303
- 4. White, H. and Christie, L.S. (1958) Queuing with Preemptive Priorities or with Breakdown. Operations Research, 6, 79-95. https://doi.org/10.1287/opre.6.1.79
- 5. Sridharan, V. and Jayashree, P.J. (1996) Some Characteristics on a Finite Queue with Normal, Partial and Total Failures. Microelectronics and Reliability, 36, 265-267. https://doi.org/10.1016/0026-2714(95)00088-J
- 6. Li, L., Wang, J.T. and Zhang, F. (2013) Equilibrium Customer Strategies in Markovian Queues with Partial Breakdowns. Computers & Industrial Engineering, 66, 751-757. https://doi.org/10.1016/j.cie.2013.09.023
- 7. Economou, A. and Kanta, S. (2008) Equilibrium Balking Strategies in the Observable Single-Server Queue with Breakdowns and Repairs. Operations Research Letters, 36, 696-699. https://doi.org/10.1016/j.orl.2008.06.006
- 8. Liu, Z. and Song, Y. (2014) The Mx/M/1 Queue with Working Breakdown. RAIRO-Operations Research, 48, 399-413. https://doi.org/10.1051/ro/2014014
- 9. Yang, D.Y. and Cho, Y.C. (2019) Analysis of the N-Policy GI/M/1/K Queuing Systems with Working Breakdowns and Repairs. Computer Journal, 62, 130-143. https://doi.org/10.1093/comjnl/bxy051
- 10. Kalidass, K. and Kasturi, R. (2012) A Queue with Working Break-downs. Computers & Industrial Engineering, 63, 779-783. https://doi.org/10.1016/j.cie.2012.04.018
- 11. Xu, B. and Xu, X. (2018) Equilibrium Strategic Behavior of Customers in the M/M/1 Queue with Partial Failures and Repairs. Operational Research, 18, 273-292. https://doi.org/10.1007/s12351-016-0264-7
- 12. 魏瑛源, 唐应辉. 延迟Min(N,D)-策略下M/G/1排队系统的离去过程[J]. 应用数学, 2018, 31(4): 820-829.
- 13. 潘取玉, 唐应辉. 在延迟Min(N,D)-控制策略下修理设备可更换的M/G/1可修排队系统及最优控制策略[J]. 数学物理学报, 2018, 38(5): 1014-1031.
- 14. 贺灵悦, 唐应辉. 带启动时间和多重休假的Min(N,V)-策略M/a/1排队系统[J]. 系统科学与数学, 2017, 37(3): 846-862.
- 15. 杨喜娟, 李忠学, 黎锁平, 武福. 带启动时间和工作故障的M/M/1/N排队系统性能分析[J]. 控制理论与应用, 2019, 36(4): 561-569.
- 16. Elhafs, E.H. and Molle, M. (2007) On the Solution to QBD Processes with Finite State Space. Stochastic Analysis and Applications, 25, 763-779. https://doi.org/10.1080/07362990701419946
- 17. 田乃硕, 岳德权. 拟生灭过程与矩阵几何解[M]. 北京: 科学出版社, 2002.
- 18. Neuts, M.F. (1981) Matrix-Geometric Solution in Stochastic Model: an Algorithmic Application. The Johns Hopkins University Press, Baltimore, MD.
- 19. Personè, V.N. and Grassi, V. (1996) Solution of Finite QBD Processes. Journal of Applied Probability, 33, 1003-1010. https://doi.org/10.2307/3214981
- 20. 叶尔骅, 张德平. 概率论与随机过程[M]. 北京: 科学出版社, 2005.