Operations Research and Fuzziology
Vol.
11
No.
02
(
2021
), Article ID:
42555
,
16
pages
10.12677/ORF.2021.112024
基于风险中性FBR和PNN的金融资产收益率序列预测模型的研究
吴新好,陆秋君
上海理工大学理学院,上海

收稿日期:2021年4月14日;录用日期:2021年5月18日;发布日期:2021年5月25日

摘要
在传统的时间序列预测模型难以揭示复杂非线性动态金融系统的内在规律的情况下,定量方法在金融市场中的应用引起了研究者和管理者的极大关注。本文基于模糊技术,结合统计工具和人工神经网络,构造了一个新的三阶段混合预测系统。在第一阶段以最小化平方和误差来拟合模糊自回归模型阶段的系数,并对样本数据进行分组。第二阶段引入风险观点,建立基于二次规划算法的模糊双线性回归模型,该模型既反映了最小二乘法的性质,又反映了无专家知识的可能性方法的性质。在第三阶段,结合概率神经网络,得到更大可能性的预测区间。通过对上证指数历史金融资产收益率序列的统计验证和分析,证明该混合预测模型的有效性。
关键词
金融资产收益率序列预测,模糊双线性回归,概率神经网络,对称三角形模糊数,风险中性
Financial Asset Yield Series Forecasting Based on Risk-Neutral Fuzzy Bilinear Regression and Probabilistic Neural Network
Xinhao Wu, Qiujun Lu
College of Science, University of Shanghai for Science and Technology, Shanghai
Received: Apr. 14th, 2021; accepted: May 18th, 2021; published: May 25th, 2021

ABSTRACT
Application of quantitative methods for forecasting purposes in financial markets has attracted significant attention from researchers and managers in recent years when conventional time series forecasting models can hardly develop the inherent rules of complex nonlinear dynamic financial systems. In this paper, based on the fuzzy technique integrated with the statistical tools and artificial neural network, a new hybrid forecasting system consisting of three stages is constructed. The sum of squared errors is minimized to determine the coefficients in fitting the fuzzy autoregression model stage for formulating sample groups to deal with data containing outliers. Fuzzy bilinear regression model introducing risk view based on quadratic programming algorithm that reflects the properties of both least squares and possibility approaches without expert knowledge is developed in the second stage. In the third stage, fuzzy bilinear regression forecasting combining with the optimal architecture of probabilistic neural network classifiers indicates that the proposed method has great contribution to control over-wide interval financial data with a certain confidence level. Statistical validation and performance analysis using historical financial asset yield series on Shanghai Stock Exchange composite index all exhibit the effectiveness of the proposed hybrid forecasting formulation compared with other forecasting methods.
Keywords:Financial Asset Yield Series Forecasting, Fuzzy Bilinear Regression, Probabilistic Neural Network, Symmetrical Triangular Fuzzy Number, Risk-Neutral

Copyright © 2021 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
近年来,定量方法在预测金融市场数据波动信息以及改善决策和投资方面发挥了重要作用。时间序列模型作为金融市场预测的工具,研究同一变量的过去观测值与当期观察值之间的关系,在商业实践中越来越重要。当对产生的数据没有充分了解,或者没有合适的解释模型将因变量与其他解释变量联系起来时,这类建模方法十分有效。提高时间序列预测的准确性是预测人员面临的一项艰巨而又具挑战性的任务,在过去40年里,从线性和非线性模型到人工智能算法,学者们引入更多样化的方法来提高预测率。
自回归差分移动平均(ARIMA)模型是使用最广泛的统计模型之一,它具有在短期准确预测和易于操作的优点。统计模型应用范围广,构建时间短,但由于金融数据具有非线性和高波动性,预测结果往往不太准确。人工神经网络(ANNs)是一种灵活的计算框架和通用逼近器,可以克服这些缺陷,适用于广泛的预测问题,具有很高的准确性。虽然人工神经网络可以取得较好的预测效果,但也存在参数确定困难、计算复杂等不足。
由于金融数据存在不稳定性,混合模型能够克服单一模型做预测时存在的缺陷,从而提高预测精度。Ince [1] 等提出了一个两阶段的预测模型,该模型采用ARIMA、协整模型和ANN技术来预测汇率。Ni [2] 等描述了一种由回归神经网络模型混合形成的混合模型,用于建模和预测外汇汇率时间序列。Patel [3] 等提出了一种包含支持向量回归(SVR)和随机森林的两阶段融合方法来预测股票市场指数的未来价值。Rather [4] 等构成了一个稳健的混合模型,包括指数平滑(ES)和递归神经网络预测股票收益。Yang [5] 等提出了一种结合ARIMA和SVR的方法来进行金融时间序列的预测。Liu [6] 等建立了基于深度学习网络的混合预测模型,对股票日收盘价序列进行预测和分析。
然而,使用单点数据的模型可能造成巨大的标准差,对不精确性和近似性的容忍度较弱。为了解决这些问题,在统计学的基础上引入模糊技术,Watada [7] 将模糊回归应用到时间序列分析。模糊回归作为一个有效工具,将传统回归分析扩展到模糊环境分析模糊情况下的复杂系统,如商业系统、社会经济系统和环境系统。模糊回归模型根据参数求解方法通常分为两类:线性规划(LP)方法 [8] 和最小二乘法(LS)方法 [9],它们相辅相成。除了上述两个类别,许多学者将模糊回归分析方法进行扩展并用于分析 [10] - [15]。
在当前研究中,学者们为了提高预测精度和减少模型的不确定性,将模糊技术融和到金融时间序列预测中,提出了新的模糊预测方法。Tseng等 [16] 将ARIMA和模糊回归模型结合(FARIMA)来进行汇率预测。Khashei等 [17] 基于ANN和模糊回归模型提出了一种新的混合方法,对不完全的金融市场数据集进行预测。Yu等 [18] 应用神经网络实现了一种新的包含不同隶属度的模糊时间序列模型来对台湾股指数据进行预测。Yolcu [19] 等提出了一种新的混合模糊时间序列方法,在模糊化阶段采用模糊c-均值聚类方法,在模糊关系确定阶段采用前向神经网络,对股票和债券交易市场的指数100进行预测。Chen [20] 等人提出了一种基于模糊时间序列、粒子群优化技术和支持向量机的方法用于台湾证券交易所资本化加权股票指数预测。一种基于模糊MA变量和模糊AR变量的模糊逻辑群关系的高阶模糊ARMA时间序列求解算法被应用于土耳其、伊斯坦布尔证券交易所的黄金价格和台湾证券交易所资本化加权股票指数 [21]。Soto等 [22] 提出一种新的基于模块化神经网络的多输入多输出模糊聚合模型,并以墨西哥证券交易所、全美证券交易商自动报价协会及台湾证券交易所的公开数据进行实证。
现有关于金融时间序列预测的文献阐述了各种组合模型,对于包含异常值的数据,从风险角度出发,可以发现同时将回归分析与智能方法整合到预测框架中更加可取。在本文中,为了使金融市场时间序列预测结果更加稳定和准确,我们利用对称三角模糊数,在不依赖于专家知识的情况下,基于风险中性模糊双线性回归(FBR)的基本概念,并结合概率神经网络(PNN),设计了一个模糊金融时间序列预测系统。该方法将模糊因变量和自变量的分解为两个分量,在强调集中、扩散趋势和可能性的同时,还可在在合理的范围内可以改变其权重和阈值,具有很强的灵活性。利用上海证券交易所综合指数(SSE)进行预测实证研究,并与其他预测模型进行比较,结果表明,所提出的方法能有效提高预测精度。
本文余下部分的结构安排如下:第2节简要介绍了模糊金融时间序列、模糊回归模型和PNN的基本原理;第3节对金融资产收益率序列预测方法的进行介绍;第4节将所提出的模型应用于上证综指的预测,并与其他预测模型进行了比较;第5节是结论。
2. 基本理论
2.1. 模糊金融时间序列
模糊理论在改进模型预测方面具有广阔的应用前景,对称模糊数 [23] 是最常用的模糊变量。通常,对称模糊数为 ,其中a和d分别表示中心和展形,隶属度函数如下:
(1)
其中, 是 在 模糊数的隶属函数,满足1) ,2) ,3)在 上递减。如果 ,对称模糊数A退化为清晰值a。
对称模糊数最常见的隶属度函数是对称三角模糊数,记作 ,其中L的形式为 。
模糊时间序列的概念最早由Song和Chissom [24] 提出,并在多个领域得到了应用。
定义1 设 的子集 是定义模糊集 的论域, 是 的集合,则 称为 上的模糊时间序列。
定义2 假定 是金融产品价格的区间序列,相对应的模糊描述为 ,称为模糊金融时间序列,其中 。
定义 3 假设 是金融产品价格的区间序列,我们定义模糊金融收益序列 如下:
(2)
模糊描述为 ,其中, 反映金融资产收益率的集中趋势, 反映金融资产收益率的非随机波动。
定义4 当中心序列 为平稳时, 称为条件平稳模糊金融收益率序列。
将区间数据转化的对称的三角模糊数,如图1所示。

Figure 1. Demonstration of transformation from interval data into symmetrical triangular fuzzy number
图1. 区间数据向对称三角模糊数转换
2.2. 模糊回归模型
设M维模糊响应变量Y和m个非模糊解释变量 ,记为 ,其中 ,。建立如下所示的模糊线性回归(FLR)模型:
(3)
其中未知参数 , 是对称模糊数, 。根据扩张定理,对称模糊输出变量Y如下所示:
(4)
其中, ,,。
模糊线性回归模型由Tanaka等 [23] 提出,描述了真实值和估计输出之间的关系,通过,将模糊回归系数求解问题转化为一个线性规划问题。以数据集模糊输出的展形估计值最小为目标函数Tanaka (1987),系数估计问题的可以表示为:
(5)
其中h是一个阈值, ,表示分配给估计模糊输出包括观测输出的关系程度。
Diamond [9] 利用三角模糊数的水平紧集之间的距离提出了一种最小二乘方法,通过最小化平方欧几里得距离,得到最小二乘回归估计:
(6)
得到 的估计如下:
(7)
其中, ,,,。
其回归区间由给定度量空间中给定数据的最小距离推导而来,通常比Tanaka等人的方法得到的区间更窄,且在计算复杂度方面,Tanaka等人的模型优于LS方法。因此,从预测的角度来看。LS方法具有较好的优越性,从计算角度看,LP方法更有效。
LP方法和LS方法不是稳健的,即使观测值与估计值有很小的误差,大量的数据也会有很大的偏差,会是参数估计产生失真现象。随后,有越来越多的学者研究FLR模型 [25] - [30]。
2.3. 概率神经网络
概率神经网络是由Specht [31] 提出的,它是一种基于监督学习算法的前馈人工神经网络,是基于贝叶斯最小风险准则开发的,在缩短训练过程的计算时间和解决非线性问题方面具有良好的性能。它一般由四层组成,即输入层、模式层、求和层和输出层。
对于输入向量 ,在输入层,该向量被分为y类, 。一个简单的概率神经网络结构如图2所示,包含n个输入变量和2个类,其中 个训练例属于第1类, 个训练例属于第2类。对于输入向量 ,每一类 的概率密度函数使用高斯径向基函数进行估计,概率密度函数 如下所示:
(8)
其中 为属于 类的训练样本的个数, 是 类的第i个训练向量, 是一个平滑参数。输出层根据求和层输出将输入向量 分类为:
(9)
其中, 是输入向量 的估计类 [32]。
概率神经网络能模拟神经系统的功能并解决实际中的复杂问题,它具有出色的分类能力;训练速度快,可以快速更新训练方案;具有很好的容错性,可以减轻异常值或可疑数据点的影响 [33]。

Figure 2. Probabilistic neural network
图2. 概率神经网络
3. 金融资产收益率序列预测方法
3.1. 模糊双线性回归模型
给定金融产品价格的n个区间观测值 ,可以得到模糊金融收益序列为 。李竹渝 [34] 等提出了金融资产收益率序列的模糊双线性回归模型,在某种程度上展形的动态变化依赖于中心的变动,鉴于此,我们对三角模糊变量的中心和展形建立模糊双线性回归模型如下:
(10)
其中, , 和 分别是观测中心和展形的 向量, 和 分别是中心和展形的误差向量。 ,,,,,, 是 的全1向量。 为中心回归模型系数向量, 和 为展形回归模型对应的系数。
注1 当 , 时,模糊双线性回归模型可以转化为模糊自回归(FAR)模型:
(11)
因此,模糊双线性回归模型可以看作是FAR模型的一种推广。
注2 令 ,,, 为常数,可得:
(12)
可以看出,我们所提出的模型在D’urso等 [35] 提出的模糊回归模型中也有所体现。
3.2. 不具备专家知识的风险中性模糊双线性回归模型
为了提高模型的预测能力,降低最小二乘方法的计算复杂度,Modarres等 [36] 基于估计模型与给定响应变量数据相等的可能性程度,建立了风险中性FLR模型,
(13)
其中 和 是模糊数,分别代表观测值和估计值, 和 分别是h水平下模糊数 和 的上下界。
(13)式中固定h的约束不等式可以转化为 ,其中 表示FLR估计模型的风险中性适应度,记作 。
注3 风险中性FLR模型阈值的约束关系与Tanaka [8] 等在研究清晰因变量时提出的约束关系一致。
Tanaka [37] 等引入二次规划(QP)来求解模糊回归模型,该模型将数据集划分为可靠组(R组)和可疑组(S组),对每组设置不同的阈值,以消除异常值带来的影响,模型如下:
(14)
Tanaka [37] 等提出的响应变量是数值型的, 。e是一个误差项,当 时属于R组, 时,属于S组。 , 和 是分析师考虑的相应正权值。
本文提出了一种无专家知识的风险中性FBR模型,结合集中趋势和展形趋势,同时考虑可能性和鲁棒性,将风险中性的FLR模型扩展到多模型。无专家知识的风险中性FBR模型可以用如下矩阵形式表:
(15)
其中, 是单位矩阵, 为加权范数, 为对角矩阵,对角元素为阈值 ,,, 和 为正权重。 , 是集合S的指示函数。
3.3. 金融资产收益率序列预测步骤
金融资产收益率序列预测模型的建立有三个主要阶段,其中包括模型确定,模型估计和模型优化。在模型确定阶段,对数据进行平稳性检验,利用自相关函数和部分自相关函数来确定模型的阶数。
模型估计阶段基于FAR模型的预测,对风险中性FBR模型进行参数估计。在专家知识较少的情况下引入误差项处理异常值的影响,把参数估计转化为二次规划问题。
模型优化阶段利用PNN对风险中性FBR模型得到的预测区间进行识别,识别出可能性更大的概率空间,从而得到较窄的预测区间。
金融资产收益率序列预测算法步骤如下:
步骤1:给定金融产品价格n个区间观测值 ,根据定义3可以得到对称三角模糊数形式 。
步骤2:利用最小二乘法确定FAR模型(11):
(16)
对未知参数的求偏导,令其为零,得到最小化问题的(局部)最优解。
步骤3:根据估计标准差 将数据分为可靠组和可疑组, 表示为:
(17)
其中 是中心的估计值。如果 满足:
(18)
则观测值属于R组,否则属于S组。其中,l是一个正数。
步骤4:利用(15)式,给权重和阈值分别赋值,计算回归参数。通过调整权重和阈值,确定出最优的估计系数。
根据估计表达式,我们可以得到估计值 、 、 ,模糊金融收益率中心和展形相应的估计值,如下:
(19)
步骤5:将上一步所得到的预测区间划分为v个相等的的子区间,将w个连续子区间视为一个类并给定编号。PNN的目标是得到包含真实值的子区间的编号。进行PNN训练时,有效变量包括t时刻中心观测值和中心估计值、t时刻中心观测和中心估计的滞后值、t时刻展形观测值和展形估计值的滞后值、t时刻时间序列估计值的上下界,t时刻时间序列估计滞后值的上下界。这个步骤的结果是得到一个w/v宽度的区间, 是一个与子区间个数有关的置信度。Proposal 1与PNN的结合称为Proposal 2。
4. 实证研究
为了验证上述方法在实际金融市场中的应用效果,我们选取上证指数2018年8月17日到2019年11月1日共292天的历史数据进行实证分析。股票价格的最高值和和最低值如图3所示,从图3(a)观察到股票价格有明显的波动趋势。对序列进行游程检验,如表1所示, 栏中p-值为0,判断序列 非平稳。从图3(b)为模糊金融收益率序列已基本上消除趋势,呈现平稳状态。对模糊金融收益率序列进行游程检验,结果见表1第3栏,p-值为0.1407,模糊金融收益率序列的中心值序列 是平稳的,进而推断模糊金融收益率序列是条件平稳的。在本文模型分析中,前281个观测值作为训练数据来估计模型的系数。最后11个观测值作为测试数据进行模型验证。
 (a)
(a) (b)
(b)
Figure 3. Trace of the time series of SSE composite index. (a) Interval observation data , (b) Fuzzy financial yield data
图3. 上证股指数据时间序列趋势图。(a) 区间观测值 ,(b) 模糊收益率序列
Table 1. Run test for the central series of financial interval time series/fuzzy financial yield series
表1. 金融区间序列/模糊收益率序列的中心序列游程检验结果
4.1. 风险中性FBR预测模型
在提出风险中性FBR模型之前,由于对观测数据的了解不足,将给定数据进行分组,然后用训练数据建立FAR模型。得到结果如下:
(20)
通过(17)式,计算样本标准差, 。令 ,根据(18)式,样本被分为两组,16个观测值在属于S组,基于(15)式,在组合权重 ,可疑组h值设置为0.4,其余数据设置0.1时,可得到风险中性FBR模型如下:
(21)
通过(21)式,可以看出,t时刻中心值随 时刻中心值的增加而增加;t时刻展形值随 时刻展形值的增加而增加,随 时刻中心值的增加而减小。显然,(21)式表明所提出的模型与李竹渝 [34] 的经济分析结果是一致的。
采用不同的系数求解方法可以得到不同的模糊回归模型,将得到的模糊回归模型通过均方根误差(RMSE)、平均百分比误差(MAPE)、方向精度(DA)值及计算性能进行比较,如表2所示(性能测度指标的计算见附录)。
Table 2. Forecasting performance comparison
表2. 模型预测性能对比
注1:我们使用线性规划、风险规避(RA)和风险中性(RN)方法在h = 0时的结果进行比较;注2:运行时结果是对每个模型过程进行1000次迭代得到的。
从表2中可以看出,无论是训练数据集还是测试数据集Proposal 1的RMSE和MAPE均小于其他方法的RMSE和MAPE,可见Proposal 1模型对上证指数模糊收益率序列的拟合能力及预测能力均优于其它方法。对于DA指标,可以观察到,相对于其他方法Proposal 1模型训练数据集方向精度为72.3%,测试数据集方向精度为80%。从计算性能来看,FBR-LP方法的运行时间略高,Proposal 1与其他5种方法的计算时间基本相同。总体来看,Proposal 1模型优于其他方法。
中心和展形的预测误差箱型图如图4所示。我们可以观察到,与其他方法相比,Proposal 1误差分布较为集中,偏离均值较少。这主要是由于在进行系数估计时从风险中性角度出发,引入误差项来处理异常值,加之权重和阈值可调节的灵活性,Proposal 1能够产生更优的结果。
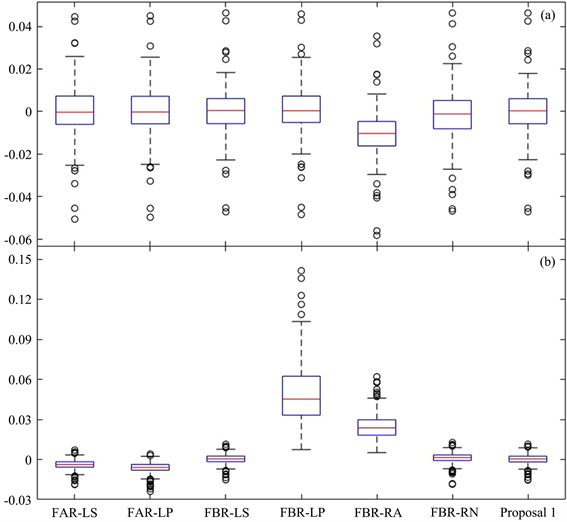
Figure 4. Comparison for boxplot description of forecasting errors in the time series of SSE composite index. (a) Error of center; (b) Error of spread
图4. 上证综指时间序列预测误差箱线图。(a) 中心误差;(b) 展形误差
注4 在风险中性模糊双线性回归中,根据约束条件估计参数,在一定h水平下,真实区间与估计区间的交集非空。通过分析结果可以看出,风险中性模糊线性回归具有较好的预测能力,但是中心观测值不在估计区间内,占训练数据的11.5%,其中有近一半与估计区间存在较小程度的偏离,如图5所示。
4.2. 基于区间预测的模型比较
当数据存在较高的波动率或离群值时,以往模型得到的估计区间可能存在不准确性,因此,可以应用智能化工具来识别非线性模式,提高预测准确度。利用构造性算法设计不同的概率神经网络体系结构,以得到最优结构,最终的网络结构包括四个输入和一个输出神经元。
Proposal 1和Proposal 2得到的测试集数据预测区间如表3所示。可以发现,Proposal 1预测区间明显宽于Proposal 2,在图5和图6中,可以清晰的观察到Proposal 1方法得到的训练数据或测试数据的预测区间宽度与Proposal 2得到的预测区间宽度存在显著差异。
在对比研究中,神经网络方法和几种传统时间序列的基本模型,如ARIMA、单指数平滑(SES)、双指数平滑(DES)、SVM、多层感知机(MLP)、反向传播(BP)神经网络和Elman神经网络进行对比,计算DES、ARIMA、MLP、SES、SVM、Elman、BP方法在95%置信水平下的预测区间,对比结果如表4所示。可以看出,由Proposal 2得到的预测区间的平均宽度为0.0083,与DES、ARIMA、MLP、SES、SVM、Elman、BP方法和Proposal 1相比,分别提高了80.52%、79.84%、78.49%、78.03%、76.91%、76.26%、74.24%和60%。
 (a)
(a) (b)
(b)
Figure 5. Forecasting intervals obtained by Proposal 1. (a) Training data; (b) Testing data
图5. Proposal 1得到的预测区间。(a) 训练数据;(b) 预测数据
Table 3. Forecasting intervals of testing data.
表3. 测试数据的预测区间
 (a)
(a) (b)
(b)
Figure 6. Forecasting intervals obtained by Proposal 2. (a) Training data; (b) Testing data
图6. Proposal 2得到的预测区间。(a) 训练集;(b) 预测集
Table 4. Comparison of interval width for the forecasting methods
表4. 预测区间宽度对比
5. 结语
在金融市场上,金融时间序列预测一直是一个热门的研究领域。我们在没有专家知识的情况下,建立了风险中性FBR模型,在利用二次规划算法进行参数估计时考虑了最小二乘和可能性方法的性质,得到最优估计系数,并利用PNN获得了宽度较窄的预测区间。通过上证指数数据集进行了实证分析,验证该方法的效果。结果表明,与其他预测方法相比,该混合模型预测区间更窄,有更高的预测精度。
该方法对于考虑无专家知识的模糊双线性回归模型引入风险观点和利用神经网络的方法具有重要的参考价值,是金融时间序列预测研究中的一种新方法。然而,也存在一些不足之处,模糊金融收益率序列的中心观测值可能会偏离估计区间,在之后的研究中在此基础上对其进行改进。本文提出的模糊回归模型是在不考虑MA变量的情况下,充分利用AR变量进行分析,最后,可以考虑中心和展形之间的非线性关系,在所提出的方法上进行扩展,并将其应用于更多的数据集,适应金融时间序列的需要。
文章引用
吴新好,陆秋君. 基于风险中性FBR和PNN的金融资产收益率序列预测模型的研究
Financial Asset Yield Series Forecasting Based on Risk-Neutral Fuzzy Bilinear Regression and Probabilistic Neural Network[J]. 运筹与模糊学, 2021, 11(02): 190-205. https://doi.org/10.12677/ORF.2021.112024
参考文献
- 1. Ince, H. and Trafalis, T.B. (2006) A Hybrid Model for Exchange Rate Prediction. Decision Support Systems, 42, 1054-1062. https://doi.org/10.1016/j.dss.2005.09.001
- 2. Ni, H. and Yin, H. (2009) Exchange Rate Prediction Using Hybrid Neural Networks and Trading Indicators. Neurocomputing, 72, 2815-2823. https://doi.org/10.1016/j.neucom.2008.09.023
- 3. Patel, J., Shah, S. and Thakkar, P. (2015) Predicting Stock Market Index Using Fusion of Machine Learning Techniques. Expert Systems with Application, 42, 2162-2172. https://doi.org/10.1016/j.eswa.2014.10.031
- 4. Rather, A.M., Agarwal, A. and Sastry, V.N. (2015) Recurrent Neural Network and a Hybrid Model for Prediction of Stock Returns. Expert Systems with Applications, 42, 3234-3241. https://doi.org/10.1016/j.eswa.2014.12.003
- 5. Yang, H.-L. and Lin, H.-C. (2016) An Integrated Model Combined ARIMA, EMD with SVR for Stock Indices Forecasting. International Journal on Artificial Intelligence Tools, 25, Article ID 1650005. https://doi.org/10.1142/S0218213016500056
- 6. Liu, H. and Long, Z. (2020) An Improved Deep Learning Model for Predicting Stock Market Price Time Series. Digital Signal Processing, 102, Article ID 102741. https://doi.org/10.1016/j.dsp.2020.102741
- 7. Watada, J. (1992) Fuzzy Time-Series Analysis and Its Forecasting of Sales Volume. In: Kacprzyk, J. and Fedrizzi, M., Eds., Fuzzy Regression Analysis, Springer, Poland, 211-227.
- 8. Tanaka, H., Uejima, S. and Asai, K. (1982) Linear Regression Analysis with Fuzzy Model. IEEE Transactions on Systems, Man, and Cybernetics, 12, 903-907. https://doi.org/10.1109/TSMC.1982.4308925
- 9. Diamond, P. (1988) Fuzzy Least Squares. Information Sciences, 46, 141-157. https://doi.org/10.1016/0020-0255(88)90047-3
- 10. Cheng, C.B. and Lee, E.S. (1999) Nonparametric Fuzzy Regres-sion—k-NN and Kernel Smoothing Techniques. Computers and Mathematics with Applications, 38, 239-251. https://doi.org/10.1016/S0898-1221(99)00198-4
- 11. Petit-Renaud, S. and Denœux, T. (2004) Nonparametric Regres-sion Analysis of Uncertain and Imprecise Data Using Belief Functions. International Journal of Approximate Reasoning, 35, 1-28. https://doi.org/10.1016/S0888-613X(03)00056-2
- 12. Wang, N., Zhang, W.X. and Mei, C.L. (2007) Fuzzy Nonparamet-ric Regression Based on Local Linear Smoothing Technique. Information Sciences, 177, 3882-3900. https://doi.org/10.1016/j.ins.2007.03.002
- 13. Roh, S.-B., Ahn, T.-C. and Prdrycz, W. (2012) Fuzzy Linear Regression Based on Polynomial Neural Networks. Expert Systems with Applications, 39, 8909-8928. https://doi.org/10.1016/j.eswa.2012.02.016
- 14. Ciavolino, E. and Calcagni, A. (2016) A Generalized Maximum Entropy (GME) Estimation Approach to Fuzzy Regression Model. Applied Soft Computing, 38, 51-63. https://doi.org/10.1016/j.asoc.2015.08.061
- 15. Jiang, H., Kwong, C.K., Chan, C.Y. and Yung, K.L. (2019) A Mul-ti-Objective Evolutionary Approach for Fuzzy Regression Analysis. Expert Systems with Application, 130, 225-235. https://doi.org/10.1016/j.eswa.2019.04.033
- 16. Tseng, F.-M., Tzeng, G.-H., Yu, H.-C. and Yuan, B.J.C. (2001) Fuzzy ARIMA Model for Forecasting the Foreign Exchange Market. Fuzzy Sets and Systems, 118, 9-19. https://doi.org/10.1016/S0165-0114(98)00286-3
- 17. Khashei, M., Hejazi, S.R. and Bijari, M. (2007) A New Hybrid Artificial Neural Networks and Fuzzy Regression Model for Time Series Forecasting. Fuzzy Sets and Systems, 159, 769-786. https://doi.org/10.1016/j.fss.2007.10.011
- 18. Yu, T.H.-K. and Huarng, K.-H. (2009) A Neural Network-Based Fuzzy Time Series Model to Improve Forecasting. Expert Systems with Applications, 37, 3366-3372. https://doi.org/10.1016/j.eswa.2009.10.013
- 19. Yolcu, U., Aladag, C.H., Egrioglu, E. and Uslu, V.R. (2013) Time-Series Forecasting with a Novel Fuzzy Time-Series Approach: An Example for Istanbul Stock Market. Journal of Statis-tical Computation and Simulation, 83, 599-612. https://doi.org/10.1080/00949655.2011.630000
- 20. Chen, S.-M. and Kao, P.-Y. (2013) TAIEX Forecasting Based on Fuzzy Time Series, Particle Swarm Optimization Techniques and Support Vector Machines. Information Sciences, 247, 62-71. https://doi.org/10.1016/j.ins.2013.06.005
- 21. Kocak, C. (2017) ARMA(p,q) Type High Order Fuzzy Time Series Fore-cast Method Based on Fuzzy Logic Relations. Applied Soft Computing, 58, 92-103. https://doi.org/10.1016/j.asoc.2017.04.021
- 22. Soto, J., Castillo, O., Melin, P. and Pedrycz, W. (2019) A New Ap-proach to Multiple Time Series Prediction Using MIMO Fuzzy Aggregation Models with Modular Neural Networks. Interna-tional Journal of Fuzzy Systems, 21, 1629-1648. https://doi.org/10.1007/s40815-019-00642-w
- 23. Tanaka, H. (1987) Fuzzy Data Analysis by Possibilistic Linear Model. Fuzzy Sets and Systems, 24, 363-375. https://doi.org/10.1016/0165-0114(87)90033-9
- 24. Song, Q. and Chissom, B.S. (1993) Fuzzy Time Series and Its Models. Fuzzy Sets and Systems, 54, 269-277. https://doi.org/10.1016/0165-0114(93)90372-O
- 25. Taheri, S.M. and Kelkinnama, M. (2002) Fuzzy Linear Regression Based on Least Absolutes Deviations. Iranian Journal of Fuzzy Systems, 9, 121-140.
- 26. Nasrabadi, E. and Hashemi, S.M. (2008) Robust Fuzzy Regression Analysis Using Neural Networks. International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems, 16, 579-598. https://doi.org/10.1142/S021848850800542X
- 27. Zeng, W., Feng, Q. and Li, J. (2017) Fuzzy Least Absolute Linear Regression. Applied Soft Computing, 52, 1009-1019. https://doi.org/10.1016/j.asoc.2016.09.029
- 28. Hesamian, G. and Akbari, M.G. (2020) A Robust Varying Coefficient Approach to Fuzzy Multiple Regression Model. Journal of Computational and Applied Mathematics, 371, Article ID 112704. https://doi.org/10.1016/j.cam.2019.112704
- 29. D’Urso, P., Massari, R. and Santoro, A. (2011) Robust Fuzzy Regres-sion Analysis. Information Sciences, 181, 4154-4174. https://doi.org/10.1016/j.ins.2011.04.031
- 30. Peters, G. (1994) Fuzzy Linear Regression with Fuzzy Intervals. Fuzzy Sets and Systems, 163, 45-55. https://doi.org/10.1016/0165-0114(94)90144-9
- 31. Specht, D.F. (1990) Probabilistic Neural Networks. Neural Net-works, 3, 109-118. https://doi.org/10.1016/0893-6080(90)90049-Q
- 32. Chung, T.-Y., Chen, Y.-M. and Tang, S.-C. (2012) A Hybrid System Integrating Signal Analysis and Probabilistic Neural Network for User Motion Detection in Wireless Networks. Expert Systems with Application, 39, 3392-3403. https://doi.org/10.1016/j.eswa.2011.09.027
- 33. Chen, A., Leung, M. and Daouk, H. (2003) Application of Neural Net-works to an Emerging Financial Market: Forecasting and Trading the Taiwan Stock Index. Computers and Operations Research, 30, 901-923. https://doi.org/10.1016/S0305-0548(02)00037-0
- 34. 李竹渝, 刘威仪, 王泰积. 金融资产收益率的模糊双线性回归[J]. 统计研究, 2009, 26(2): 68-73.
- 35. D’Urso, P. and Gastaldi, T. (2000) A Least-Squares Approach to Fuzzy Linear Re-gression Analysis. Computational Statistics and Data Analysis, 34, 427-440. https://doi.org/10.1016/S0167-9473(99)00109-7
- 36. Modarres, M., Nasrabadi, E. and Nasrabadi, M.M. (2004) Fuzzy Linear Regression Analysis from the Point of View Risk. International Journal of Uncertainty Fuzziness and Knowledge Based Systems, 12, 635-649. https://doi.org/10.1142/S0218488504003120
- 37. Tanaka, H. (1997) Fuzzy Linear Regression Combining Central Tendency and Possibilistic Properties. Proceedings of 6th International Fuzzy Systems Conference, 1, 63-68.
附录
本研究采用了三种常用的绩效衡量方法,具体如下:
1) 均方根误差(RMSE)
2) 平均绝对百分比误差(MAPE)
3) 方向精度(DA)
其中, ,,。
