Journal of Water Resources Research
Vol.05 No.03(2016), Article ID:17749,9
pages
10.12677/JWRR.2016.53033
Comparative Study on Parameter Estimation Methods of Generalized Extreme Value Distribution
Ling Xiao, Shuangchao Lei
Zunyi Survey and Design Institute of Water Conservancy and Hydropower, Zunyi Guizhou

Received: May 16th, 2016; accepted: Jun. 3rd, 2016; published: Jun. 6th, 2016
Copyright © 2016 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
Research on parameter estimation of Generalized Extreme Value distribution based on the moment, the probability weighted moment and the higher probability weighted moments. The two examples of Wujia Yuanzi and Jiang Bin stations annual maximum flow series were analyzed by the three parameter estimation methods of GEV distribution, which included the moment estimation, the probability weighted moment estimation and the higher probability weighted moment estimation. The results indicate that using the higher PWMs to fit the large flood values are much better than the moment and the probability weighted moment, and we can use it to estimate the parameters of the flood frequency distribution. The Monte Carlo experiments indicate that the SE, Bias and RMSE in the design floods of different return periods which based on the higher probability weighted moments are smaller and the PWMs have higher accuracy than the moment and the probability weighted moment.
Keywords:Generalized Extreme Value Distribution, Higher Probability Weighted Moments, Method of Moment, Parameter Estimation

广义极值分布参数估计方法比较研究
肖玲,雷双超
遵义水利水电勘测设计研究院,贵州 遵义

收稿日期:2016年5月16日;录用日期:2016年6月3日;发布日期:2016年6月6日

摘 要
研究广义极值分布参数估计的普通矩法、普通概率权重矩法和高阶概率权重矩法。以黔北地区五家院子和江滨水文站年最大洪峰流量序列为例,选用广义极值分布,应用普通矩法、普通概率权重矩和高阶概率权重矩进行参数估计,并对各方法的拟合效果和参数估计结果进行分析比较。结果表明:与普通矩法和普通概率权重矩法相比,高阶概率权重矩法能更好的拟合洪水序列的高尾部分洪水值,可以进行洪水频率分布的参数估计。蒙特卡洛试验表明:高阶概率权重矩法计算出的不同重现期洪水设计值的SE、Bias和RMSE较小,与常用的矩法、普通概率权重矩法相比,高阶概率权重矩法具有较高的精度。
关键词 :广义极值分布,高阶概率权重矩,普通矩法,参数估计

1. 引言
在实际洪水频率分析计算中,当点绘年最大洪峰流量序列的经验频率时,经验点据常常出现两段或多段的分散区,重现期较大的洪水设计值一般是根据大中洪水值的趋势进行外推。常用的参数估计方法有极大似然(ML)、矩法(MOM)、线性矩(LM)、概率权重矩(PWM)、最小二乘(LS)和间隔最大积(MPS)等 [1] ,其计算的理论频率曲线通常与经验点据的中下部分拟合较好,而曲线的中上端与经验点据拟合偏差较大,导致推求的洪水设计值过低不利于大坝及下游的安全运行。20世纪90年代,Wang Q.J.博士 [2] 提出了采用高阶概率权重矩洪水频率分布参数估计方法,该法能赋予大洪水值更多的权重,取得了较好的拟合效果。目前,我国西北农林科技大学宋松柏教授等人将这一理论方法应用到GEV分布参数估计中,并以陕北地区年最大洪峰流量序列为例,研究了高阶概率权重矩在GEV分布参数估计中的应用 [3] 。本文以黔北地区五家院子和江滨水文站年最大洪峰流量序列为例,并对GEV分布参数的高阶与普通概率权重矩法及普通矩法拟合结果进行分析与比较,进一步研究高阶概率权重矩在推求GEV分布参数中的应用与普适性。
2. 广义极值分布
广义极值分布(Generalized extreme value distribution,简记为GEV)的概率密度函数为:
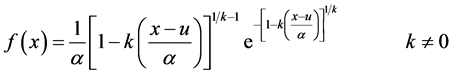 (1)
(1)
其分布函数表达式为:
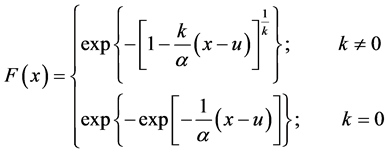 (2)
(2)
式中: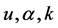 分别为分布的形状参数、位置参数和尺度参数。当
分别为分布的形状参数、位置参数和尺度参数。当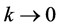 时为极值I型,即Gumbel分布;当
时为极值I型,即Gumbel分布;当 时为极值II型,即Fréchet分布;当
时为极值II型,即Fréchet分布;当 时为极值III型,即Weibull分布 [1] - [5] 。
时为极值III型,即Weibull分布 [1] - [5] 。
式(2)的逆函数形式为:
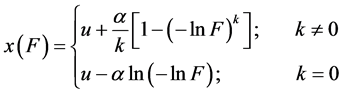 (3)
(3)
式中: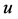 、
、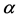 和
和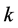 意义同上。
意义同上。
3. 参数估计方法
3.1. 高阶概率权重矩法
概率权重矩法(PWM)由Greenwood (1979)等人 [6] 首先提出,假定随机变量X的分布函数为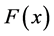 ,则概率权重矩的定义为:
,则概率权重矩的定义为:
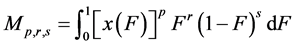 (4)
(4)
式中: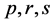 为实数,
为实数,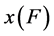 为分布函数的逆函数。当
为分布函数的逆函数。当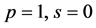 时,概率权重矩为:
时,概率权重矩为:
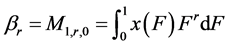 (5)
(5)
式中,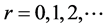 为概率权重矩的阶数。式(5)表明,当概率权重矩的阶数增大时,会赋予大值
为概率权重矩的阶数。式(5)表明,当概率权重矩的阶数增大时,会赋予大值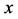 较多的权重。
较多的权重。
给定一长度为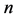 的升序排列样本
的升序排列样本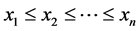 ,高阶概率权重矩的无偏估计量可通过式(6)来计算:
,高阶概率权重矩的无偏估计量可通过式(6)来计算:
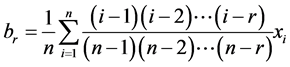 (6)
(6)
式(3)中,当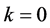 时,Greenwood (1979) [6] 给出了GEV分布的概率权重矩为:
时,Greenwood (1979) [6] 给出了GEV分布的概率权重矩为:
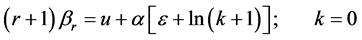 (7)
(7)
式中,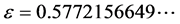 为欧拉常数。
为欧拉常数。
当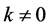 时,Wang Q.J. [2] 推求了GEV分布的概率权重矩为:
时,Wang Q.J. [2] 推求了GEV分布的概率权重矩为:
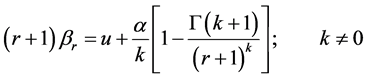 (8)
(8)
式中: 为gamma函数。
为gamma函数。
由式(4)可知,要求解GEV分布函数中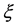 ,
,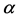 ,
,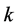 三个参数,需要列三个方程式进行求解。令概率权重矩的阶数
三个参数,需要列三个方程式进行求解。令概率权重矩的阶数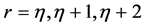 ,并分别代入式(9),有
,并分别代入式(9),有
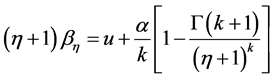 (9)
(9)
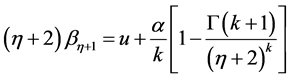 (10)
(10)
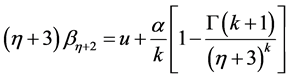 (11)
(11)
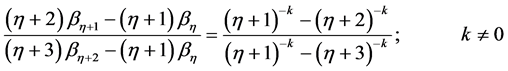 (12)
(12)
同理,当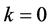 时,GEV分布的概率权重矩为:
时,GEV分布的概率权重矩为:
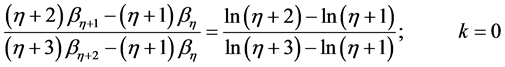 (13)
(13)
上述式中GEV分布的样本概率权重矩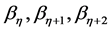 可用式(6)计算出的无偏估计量
可用式(6)计算出的无偏估计量 代替,采用适当的公式可求出参数
代替,采用适当的公式可求出参数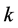 ,
,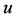 ,
, 。由于没有给出
。由于没有给出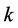 的直接表达式,采用常规的迭代法计算量很大,因此,可采用计算机数值算法来求解。
的直接表达式,采用常规的迭代法计算量很大,因此,可采用计算机数值算法来求解。
式(12)两边同时减去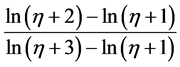 有:
有:
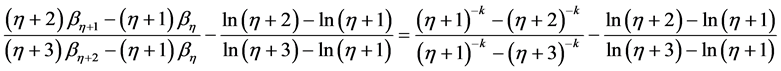
令上式右边为
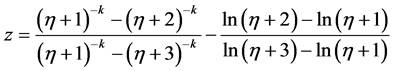 (14)
(14)
给定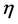 值,可采用二次函数拟合式估算
值,可采用二次函数拟合式估算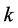 值:
值:
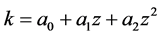 (15)
(15)
设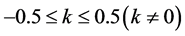 ,分别给定
,分别给定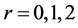 (即普通概率权重矩)、
(即普通概率权重矩)、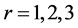 、
、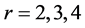 、
、 、
、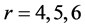 ,利用式(14)求出不同阶数对应的
,利用式(14)求出不同阶数对应的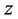 值,并对
值,并对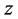 和
和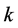 的关系进行拟合,得出不同阶数下式(15)中的系数
的关系进行拟合,得出不同阶数下式(15)中的系数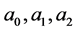 ,结果见表1。
,结果见表1。
通过式(14)计算出不同阶数对应的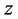 值后,结合表1中相应阶数的各系数值,代入式(15)中求出GEV分布的形状参数
值后,结合表1中相应阶数的各系数值,代入式(15)中求出GEV分布的形状参数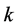 。将形状参数
。将形状参数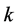 值代入式(9)和式(10)中,计算GEV分布的尺度参数
值代入式(9)和式(10)中,计算GEV分布的尺度参数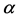 和位置参数
和位置参数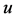 ,其参数表达式分别为:
,其参数表达式分别为:
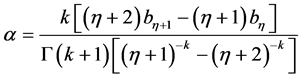 (16)
(16)
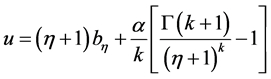 (17)
(17)
3.2. 普通矩法
矩法是用样本矩估计总体矩,并通过矩和参数之间的关系来估计频率曲线参数的一种方法。设随机变量X服从GEV分布函数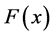 ,则X的r阶中心矩为 [7] :
,则X的r阶中心矩为 [7] :
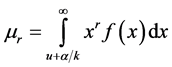 (18)
(18)
式中: 为GEV分布的概率密度函数。
为GEV分布的概率密度函数。
令式(1)中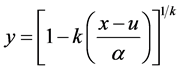 并带入式(18),可计算出X的一阶、二阶和三阶中心矩如下:
并带入式(18),可计算出X的一阶、二阶和三阶中心矩如下:
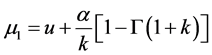
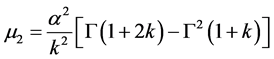
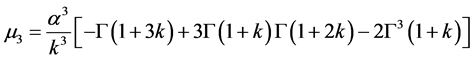
由以上式子可得到偏态系数Cs的表达式为:
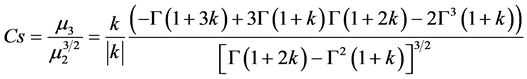 (19)
(19)
设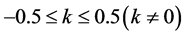 ,利用式(19)求出不同
,利用式(19)求出不同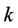 对应的
对应的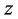 值,并对
值,并对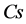 和
和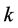 的关系进行拟合(结果见图1),得出其关系式,并通过其关系式求
的关系进行拟合(结果见图1),得出其关系式,并通过其关系式求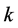 的初值,再利用牛顿迭代法计算出满足条件的
的初值,再利用牛顿迭代法计算出满足条件的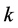 值。将求出的
值。将求出的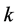 值带入式(20)、(21)即可求解参数
值带入式(20)、(21)即可求解参数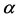 和
和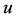 。
。
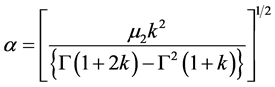 (20)
(20)
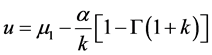 (21)
(21)
4. 实例应用
前文简述了普通矩法、普通概率权重矩法及高阶概率权重矩法在GEV分布参数估计中的计算方法,为了分析比较三种方法的优劣,以黔北地区五家院子水文站和江滨水文站实测年最大洪峰流量序列为例,进行GEV分
Table 1. Coefficients a0, a1 and a2 and the absolute error for different higher probability weighted moments
表1. 不同高阶概率权重矩系数a0,a1和a2的取值及绝对值偏差统计表
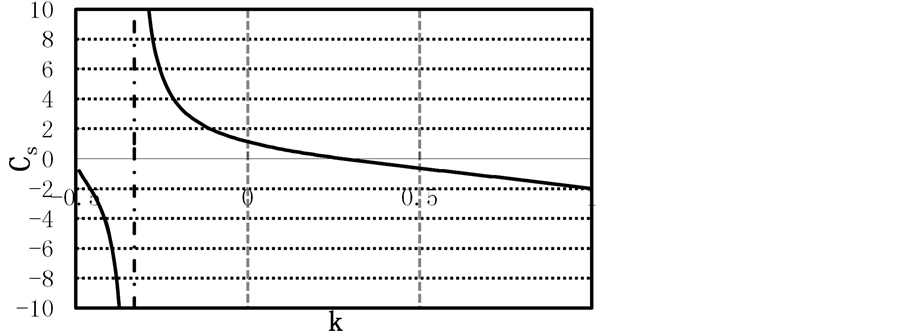
Figure 1. Relationship between the Cs and k for the GEV distribution
图1. GEV分布中Cs和k的关系曲线
布的参数估算研究。
利用上述原理及公式,计算出不同方法下各测站GEV分布参数值,结果见表2。绘制各测站不同阶PWM的GEV分布理论频率曲线,拟合结果见图2。
从图2可以看出,随着概率权重矩阶数的提高,理论频率曲线的中上部与年最大洪峰流量中的大洪水段点据拟合越好。
根据图2中的拟合结果,选出其中拟合较好的r = 3,4,5阶和普通PWM (r = 0,1,2)的理论频率曲线,并将之与普通矩法的拟合情况进行对比,结果见图3。
从图3中可以看出,r = 3,4,5阶的PWM比普通PWM能更好的拟合洪水的高尾部点据,且均优于普通矩法。在水利工程规划设计中,尤其是西南地区,降水充沛,量级大,较多的考虑大中洪水段对水利工程的影响,而高阶概率权重矩法具有较好的优势,可以在洪水频率分布参数估计中加以应用。
5. Monte Carlo试验
蒙特卡洛试验是对使用不同高阶概率权重矩法估计GEV分布参数时对不同重现期设计洪水值的影响评价 [1] [8] - [10] 。
为了进一步说明高阶PWM在GEV分布参数估计中的精度,本文利用具有更高灵活度的Wakeby分布模型 [11] ,设样本容量为n = 30,模拟N = 100000组序列。利用模拟出来的序列计算普通矩法及不同高阶概率权重矩下GEV分布参数值,并分别计算重现期为50年和100年的洪水设计值(即分位数x(F = 0.98),x(F = 0.99)),
Table 2. The estimated GEV distribution parameters of several methods
表2. 各测站几种GEV分布参数估计方法结果统计表
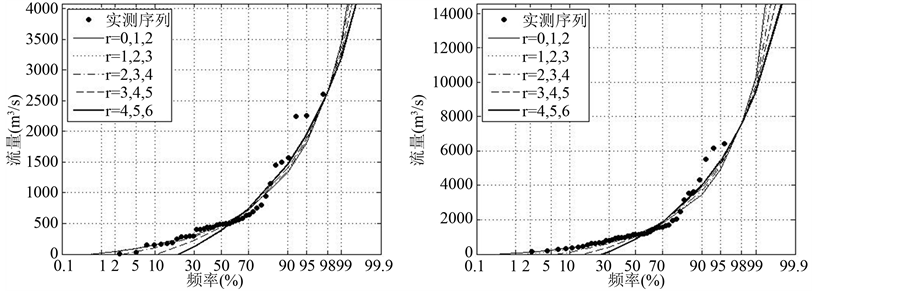 (I) 五家院子 (II) 江滨
(I) 五家院子 (II) 江滨
Figure 2. Fitting of the GEV distribution using different higher PWMs to annual maximum flows at different stations
图2. 不同高阶PWM下GEV分布理论曲线与年最大洪峰流量频率曲线拟合
最后采用标准误差(SE)、偏差(Bias)、和均方根误差(RMSE)进行评价,结果见表3,表4。
从表3,表4可以看出,基于5参数Wakeby分布模拟的数据,利用GEV分布函数估计出来的不同高阶PWM下各重现期设计值的SE、Bias和RMSE随着阶数的增大总体呈先减小后增大趋势,其中,Bias的这种趋势特别显著。当 时误差较大,
时误差较大, 时误差最小。同时,普通矩法的SE、Bias和RMSE均比前两种方法
时误差最小。同时,普通矩法的SE、Bias和RMSE均比前两种方法
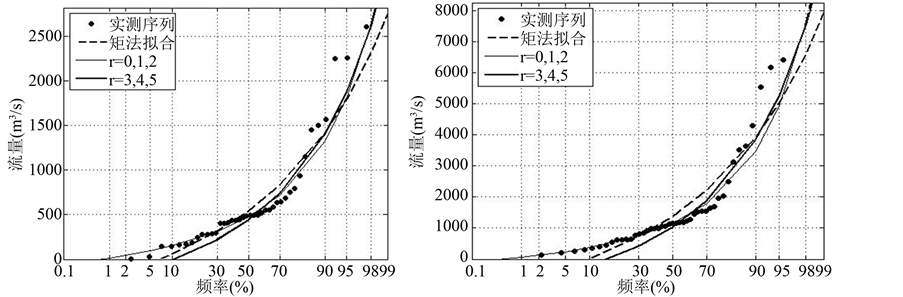 (I) 五家院子 (II) 江滨
(I) 五家院子 (II) 江滨
Figure 3. Fitting of the GEV distribution using different methods to annual maximum flows at different stations
图3. 不同方法下GEV分布理论曲线与年最大洪峰流量频率曲线拟合
Table 3. SE, Bias and RMSE in x(F=0.98) estimates from fitting the GEV distribution with Wakeby samples
表3. 基于Wakeby分布样本的GEV分布在x(F = 0.98)时设计值的标准误差,偏差和均方根误差
Table 4. SE, Bias and RMSE in x(F = 0.99)estimates from fitting the GEV distribution with Wakeby samples
表4. 基于Wakeby分布样本的GEV分布在x(F = 0.99)时设计值的标准误差,偏差和均方根误差
大,其中Bias和RMSE的增幅较大。因此,蒙特卡洛试验进一步表明高阶概率权重矩法在估算GEV分布参数时,具有明显的优势。但需要注意的是,可以适当的提高阶数,但不能盲目的提高阶数,当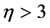 (即阶数
(即阶数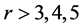 )时,误差会增大。
)时,误差会增大。
6. 结论
本文根据Wang高阶概率权重矩法的GEV分布参数估计理论,研究了不同高阶PWM在GEV分布参数估计中的应用,并以黔北地区五家院子水文站和江滨水文站的年最大洪峰流量序列为例,分别用普通PWM、普通矩法和高阶PWM估计GEV分布参数值,最后通过蒙特卡洛试验对三种方法的SE、Bias和RMSE进行分析。结果表明,随着概率权重矩阶数的提高,GEV分布曲线与年最大洪峰流量中的大中洪水段点据拟合越好,而矩法在大中洪水段偏离较大。蒙特卡洛试验表明,高阶PWM法(当 时)计算出的不同重现期洪水设计值的SE、Bias和RMSE较小,与常用的普通矩法、普通PWM法相比,高阶概率权重矩法具有较高的精度,能够在GEV分布参数估算中加以应用。
时)计算出的不同重现期洪水设计值的SE、Bias和RMSE较小,与常用的普通矩法、普通PWM法相比,高阶概率权重矩法具有较高的精度,能够在GEV分布参数估算中加以应用。
文章引用
肖 玲,雷双超. 广义极值分布参数估计方法比较研究
Comparative Study on Parameter Estimation Methods of Generalized Extreme Value Distribution[J]. 水资源研究, 2016, 05(03): 262-270. http://dx.doi.org/10.12677/JWRR.2016.53033
参考文献 (References)
- 1. 陈子燊, 刘曾美, 陆剑飞. 广义极值分布参数估计方法的对比研究[J]. 中山大学学报(自然科学版), 2010, 49(6): 105-109. CHEN Zishen, LIU Zengmei, LU Jianfei. Comparative analysis of parameter estimation methods of general extreme value dis-tribution. Acta Scientiarum Naturalium Universitatis Sunyatseni, 2010, 49(6): 105-109. (in Chinese)
- 2. WANG, Q. J. Using higher probability weighted moments for flood frequency analysis. Journal of Hydrology, 1997, 194(1): 95-106. http://dx.doi.org/10.1016/S0022-1694(96)03223-4
- 3. 李杨, 宋松柏. 高阶概率权重矩在洪水频率分析中的应用[J]. 水利发电学报, 2013, 32(2): 14-21. LI Yang, SONG Songbai. Application of higher-order probability-weighted momentsto flood frequency analysis. Journal of Hydroelectric Engineering, 2013, 32(2): 14-21. (in Chinese)
- 4. JENKINSON, A. F. The frequency distribution of the annual maximum(or minimum)values of meteorological elements. The Quarterly Journal of the Royal Meteorological Society, 1955, 81(348): 158-171. http://dx.doi.org/10.1002/qj.49708134804
- 5. COLES, S. An introduction to statistical modeling of extreme values. New York: Springer Verlag, 2001.
- 6. GREENWOOD, J. A., LANDWEHR, J. M., MATALAS, N. C. and WALLIS, J. R. Probability weighted moments: definition and relation to parameters of distribution expressible in inverse form. Water Resources Research, 1979, 15(5): 1049-1054. http://dx.doi.org/10.1029/WR015i005p01049
- 7. RAMACHANDRA RAO, A., HAMED, K. H. Flood frequency analy-sis. CRC Press, 2000.
- 8. WANG, Q. J. Unbiased estimation of probability weighted moments and partial probability weighted moments from systematic and historical flood information and their application to estimating the GEV distribution. Journal of Hydrology, 1990, 120(1-4): 115-124.
- 9. 卢安平, 赵林, 郭增伟, 等. 基于Monte Carlo法的极值分布类型及其参数估计方法比较[J]. 哈尔滨工业大学学报, 2013, 45(2): 88-95. LU Anping, ZHAO Lin, GUO Zengwei, et al. A comparative study of extreme value distribution and parameter estimation based on the Monte Carlo method. Journal of Harbin Institute of Technology, 2013, 45(2): 88-95. (in Chinese)
- 10. WANG, Q. J. Using partial probability weighted moments to fit the extreme value distributions to censored samples. Water Resources Research, 1996, 32(6): 1767-1771. http://dx.doi.org/10.1029/96WR00352
- 11. LANDWEHR, J. M., MATALAS, N. C. Estimation of parameters and quantiles of Wakeby distributions 2. Unknown lower bounds. Water Resources Research, 1979, 15(6): 1373-1379. http://dx.doi.org/10.1029/WR015i006p01373
