Journal of Water Resources Research
Vol.
09
No.
03
(
2020
), Article ID:
35916
,
9
pages
10.12677/JWRR.2020.93033
Calculation of Rating Curve at Cross Section in Complex Natural River with Few Hydrology Data
Fahong Zhang, Qinghua Yue, Jing Guo
Power China Huadong Engineering Corporation Limited, Hangzhou Zhejiang

Received: Apr. 13th, 2020; accepted: May 19th, 2020; published: Jun. 2nd, 2020

ABSTRACT
In designing and planning of hydropower project, the rating curve at dam site, powerhouse place etc. have an important effect on determining the project key parameters, such as the scale and designing of spillway and energy dissipation works, the installation elevation of powerhouse and turbine, as well as installed capacity and annual power generation amount of the project. However, in the early phase of the most hydropower projects, it often lacks gauged water level and discharge data, only the data of cross section, water level of gauged time, and few investigating historical water level data are available. The rating curve at these project feature cross sections is generally developed by hydraulic methods with these available data; what’s more, the river situation in these places is generally complex. How to get a rational result becomes more difficult and important. Combing the practical engineering design, taking K hydropower project in U country in Africa whose river channel is characterized by a complex flow regime as case study, the rating curve at project feature cross sections such as dam site is developed by the tools of the Manning formula, weir-flow formula, Bernoulli equation on the premise of lacking gauged water level and discharge data. The approach and method may provide references for a similar situation for the determination of the rating curve in the river lacking hydrology data.
Keywords:Lack of Hydrology Data, Complex Natural River, Rating Curve, Manning Formula, Weir Flow Formula

缺乏水文资料的复杂天然河道断面水位流量关系曲线计算
张发鸿,岳青华,郭靖
中国电建集团华东勘测设计研究院有限公司,浙江 杭州

收稿日期:2020年4月13日;录用日期:2020年5月19日;发布日期:2020年6月2日

摘 要
在水电工程规划设计中,坝厂址等位置的水位流量关系曲线对于确定泄洪建筑物和消能建筑物的规模、厂房及水轮机组的安装高程、电站装机容量及发电量效益等指标的确定都具有重要的影响。但在多数水电项目的前期阶段,往往缺乏实测的水位、流量资料,只有河道的大断面资料、测时水面线及少数历史洪痕调查资料,各工程断面水位流量关系曲线往往利用上述资料根据水力学方法来推求;加之上述点位河道情况往往较为复杂,如何算出合理的成果显得比较困难和重要。本文结合工程设计实践,以工程河段河流流态较为复杂的非洲U国K水电站项目为案例,用曼宁公式、堰流公式、伯努利方程为工具,在缺乏实测水位、流量资料的前提下,推求工程坝址等特征断面水位流量关系曲线。文中的思路和方法,对于类似缺乏水文资料情况下确定水位流量关系曲线有较好的参考和借鉴作用。
关键词 :缺乏水文资料,复杂天然河道,水位流量关系曲线,曼宁公式,堰流公式

Copyright © 2020 by author(s) and Wuhan University.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
在水电工程规划设计中,往往需要推求坝址、厂址等断面处天然河道的水位流量关系曲线。这些位置的水位流量关系对于确定正常蓄水位、泄洪和消能建筑物的规模、厂房及水轮机组的安装高程、围堰高程、电站发电量等工程效益指标的确定都具有重要的影响。而一些中小河流由于处在交通不便的偏僻山区,距离水文站较远,往往缺乏实测水位、流量资料;即使临时设立水文观测站点,短期内也很难观测到高水和低水部分的实测点据,这些都给推求坝、厂址的水位流量关系曲线带来较大困难。
一般来讲,河道断面水位~流量关系曲线的推求常采用以下几种方法:
1) 利用上下游已有特征断面水位~流量关系成果。当水电站设计断面附近有已知水位流量关系曲线的参证河床断面(一般为水文站)时,在水电站与该断面之间增测若干河床横断面,利用伯努利能量方程推求设计断面的水位流量关系 [1]。
2) 水力学方法。用曼宁公式对位于顺畅河道中的断面进行计算;对于河道有纵向明显跌落(如跌砍、瀑布等)或横向明显缩放(如卡口、断面突变段)等,可将此处断面概化为无底坎宽顶堰,利用水力学堰流公式进行计算 [2]。当设计断面有实测水位资料,上下游断面有可供移用的流量资料时,可根据实测水位及移用流量资料拟定水位流量关系;也可根据水位相关移用上下游断面水位流量关系,特别注意区间流量的改正 [3]。
3) 长期测流拟定。在工程特征断面位置布置水尺并进行水位、流量数据的长期观测,以期通过实测数据来建立水位~流量关系。并利用如 法、史蒂文森法等方法进行高水外延 [4]。
4) 明渠恒定均匀流推求。河床断面处水流按恒定均匀流考虑,利用明渠恒定均匀流公式推求工程点位处不同流量等级下的水位,并最终建立水位流量关系 [5]。在国外工程设计中,有时要求根据HEC-RAS软件计算河道水面线后推求所需断面的水位流量关系曲线 [6]。
工程区域实测水位、流量数据及历史洪调资料的数量、可靠性对水位流量关系的计算及成果质量有着直接影响 [7]。在水电工程的实际规划设计中,多数工程位置偏远,区域河道附近上下游往往无水文站点,各工程点位处往往缺乏实测水位、流量资料,通常只有河道的大断面资料及测时水面线、极少数历史洪调资料。项目前期有限的设计周期也制约了设站长期观测水位、流量后再拟定水位~流量关系曲线工作的开展 [8]。尤其在近30年的水电开发热潮中利用了大量宜开发点位后,后续待开发的水电项目将更多地面临在缺乏水文资料的复杂天然河道断面(坝厂址河段往往有瀑布、跌水、急滩,深潭、沙洲等影响水力学条件的地貌存在,尤其对于引水式电站)分析计算水位流量关系曲线的情形。
因此,如何结合工程实际,充分利用断面资料和极少数的水文资料,选择合适的水力学、水动力学方法和选用恰当的参数来推求复杂天然河道断面水位流量关系曲线就变得非常现实和重要。
2. 研究方法
可用于天然河道水位流量关系曲线计算的水力学、水动力学方法较多,在水电工程中应用较为广泛的一般有以下3种:
2.1. 曼宁公式
曼宁公式在计算天然河道的过流能力、水位流量关系曲线中,应用非常广泛和普遍。曼宁公式计算公式如下:
(1)
式中:Q为洪峰流量,m3/s;n为河道糙率;I为水面比降;A为有效过水断面面积,m2;R为水力半径,m。
曼宁公式在计算山区性河道,尤其是在计算工程点位上下游一定范围内较为顺直的山区性河道的水位流关系曲线中有较好的效果。
2.2. 堰流公式
当具有自由表面的水流,流经闸墩、桥墩、围堰、涵洞的进口等形成侧向收缩时或天然河道断面由于明显缩窄等形成收缩时,可按宽顶堰流来分析,称为无底坎宽顶堰。其计算公式如下:
(2)
式中: 为侧收缩系数; 为淹没系数;m为自由溢流的流量系数;b为每孔净宽;n为闸门孔数;H0为包括行进流速水头的堰上水头,即 。
堰流公式在计算工程断面有一定横向收缩或断面下游为跌水、瀑布等情况的山区性河道的水位流关系曲线中有较好的效果。
2.3. 一维恒定非均匀渐变流计算
从缓流河道中水面线的特性可知,无论下游有壅水建筑物还是有跌水急滩,其上游的壅水或落水水面线,都是以河道天然水面线作为渐近线。利用河道水面线这些特性,只要将起推断面设置在离计算河段足够远处,中间河段沿程水力摩阻可以基本上消除起始断面水位假设的误差,如图1所示。若起推水位为人为假定时,一般需经过若干次试算。若图中所示的起推断面足够远,起算误差调整段较长,试算次数会较少,甚至一、两次即可满足要求;若起算误差调整段较短,则试算次数需较多 [9]。

Figure 1. Schematic diagram of calculation error of constant flow surface curve
图1. 恒定流水面线计算误差示意
笔者在工程实践中曾采用一维恒定非均匀渐变流,推算设计断面所在河段不同流量下的水面线或根据几个断面同时刻水位来反推对应流量,从而根据水面线计算成果拟定设计断面水位流量关系,然后用水文调查资料进行合理性分析定线。
此外,本方法还可用于无实测水文资料时断面的高水外延及上下游断面间水位流量关系曲线成果的合理性分析。
3. 应用实例
3.1. 流域及工程概况
非洲U国的K水电站是该国第一大河上规划开发7个梯级电站中的第三级。K水电站开发任务以发电为主,坝址处流域面积为336,000 km2,水库总库容7987万m3,调节库容4553万m3,具有日调节能力。水电站采用长引水开发方式,尾水出口在坝址下游约10 km处。从坝址上游1 km至尾水出口处之间的河道中,有多处瀑布、跌水、急滩,沙洲等,河道断面及水流形态十分复杂。
3.2. 流域及工程概况
坝址以上流域降雨量较为丰沛,年降雨量在900~2000 mm之间。在坝址上游有受上游库容巨大的V湖和K湖的调节,径流的日内变化非常小,月内变化也一般不大;洪水的涨落幅度一般不大,洪水过程较为平缓均匀,洪水的年际变幅亦较小,历年实测年最大洪峰流量最大值为2298 m3/s仅为最小值632 m3/s的3.64倍。K电站坝址处各月多年平均流量、设计洪峰流量成果见表1、表2。
Table 1. The annual runoff distribution at K Power Station
表1. K电站年内径流分配表
Table 2. The design flood peak flow at K Power Station
表2. K电站设计洪峰成果
K水电站在前期规划阶段只有工程区域各涉河点位河道大断面资料及测时水位,无测时水位对应的流量资料。
3.3. 水位流量关系曲线计算
3.3.1. 计算思路
在采用任何水力学方法进行断面水位流量关系曲线计算时,都需要对水力学公式中的参数进行率定,并对计算成果进行验证。对于K水电站项目,因无实测水文数据,故参阅相关水力学书籍粗选各断面糙率n、流量系数m等参数。然后假定不同的测时流量,并视断面间计算水位值与实测水位值的差别情况调整不同断面间的同一参数取值,直到几个断面的测时水面线所对应流量一致为止。
另外,宜采用至少两种方法来进行测时流量反推,减少技术方法或参数粗拟因素所造成的成果误差;在确定出测时水面线、洪痕所对应流量后,便可用这些水位、流量点据来进行水力学计算的参数率定和成果验证 [10]。
3.3.2. 反推测时流量
根据测量成果知,K电站所在河流在DM2断面(导流明渠入口)有一处落差约2.14 m的跌坎,在DM3断面(发电引水隧洞入口)有一处落差约1.93 m的跌坎,DM4断面(坝址)下游约30 m有一处落差约6.57 m的瀑布,DM2 (导流明渠入口上游)~DM4距离为388 m。此3处断面均可概化为水力学中的无底坎宽顶堰(自由出流或淹没出流)。此外,3处均为山区性河道天然断面,亦可用曼宁公式计算其水位流量关系曲线 [11]。
由于测量区域无较大支流汇入,各断面的测时流量基本一致,因此,可利用恒定流方程根据各个断面的测时水面线,推算测时流量,并以此流量来反推和优化3种方法中的相关参数。在用曼宁公式和堰流公式计算时,均应考虑河道中巨石、沙洲对过水断面的影响。
用曼宁公式计算时,查天然河道糙率表得此段河道糙率取值为0.055~0.085,计算得断面DM1~DM4的测时流量为1059~1066 m3/s,均值1064 m3/s。
用堰流公式计算时,流量系数据该断面及上下游河段形态,查水力学手册得取值为0.350~0.375,计算得出DM1~DM4的测时流量范围为1018~1125 m3/s,均值1077 m3/s。
用一维恒定流计算(作者选用MIKE 11水动力软件作为计算工具)时,以DM4断面的测时水位为下边界,以DM1断面的假定流量为上边界,给定不同试算流量直至DM1~DM3处模型计算水位与实测水位最为接近为止。由于本流域受上游维多利亚湖调蓄后,径流变化平缓,以水面线测量月份的平均流量作为试算起推流量。试算得出DM1~DM4的测时水面线流量范围为1027~1076 m3/s,平均值为1054 m3/s。
由上述计算结果可知,用3种不同原理、不同方法计算出来的测时水面线的流量较为接近,证明概化的堰流模型、曼宁公式及MIKE 11软件水动力模块的参数选取较为合理,计算结果有较高的可信度。最终选取MIKE 11软件恒定流模块所算出的测时水面线对应流量平均值1054 m3/s作为测时水面线流量。
3.3.3. 各断面水位流量关系曲线计算
1) 导流明渠入口(DM2)
分别用堰流公式和曼宁公式计算此断面水位流量关系曲线。根据测时水面线及其相应流量点据进行模型参数率定。两个公式中各参数选取情况如下:
堰流公式:
淹没系数:经计算,此断面堰上水头为H0为3.51 m,堰下水头hs为3.28 m,hs/H0 = 0.934。查阅水力学手册得此处为淹没出流,为0.78;
流量系数:根据河道现场情况,查水力学手册中流量系数表,并结合实测点据成果,率定得0.365。
曼宁公式:
水力学比降:此段河道的水面比降同时受到DM1断面跌坎和DM4断面下游处瀑布的影响,断面比降取河段比降,即:(1027.28 − 1025.49)/387.9 = 0.0046;
糙率:据河道现场情况查阅糙率表,得其取值在0.05~0.07之间;据测时水面线实测流量点据,率定得其河道综合糙率为0.057。
2) 坝址断面(DM4)
分别用堰流公式和曼宁公式计算此断面水位流量关系曲线。根据测时水面线及其相应流量点据进行模型参数率定和成果验证。DM4断面两公式中各参数选取情况与DM2断面类似,在此不再赘述。
导流明渠入口(DM2)和坝址(DM4)由上述两种方法计算所得水位流量关系曲线见图2和图3。
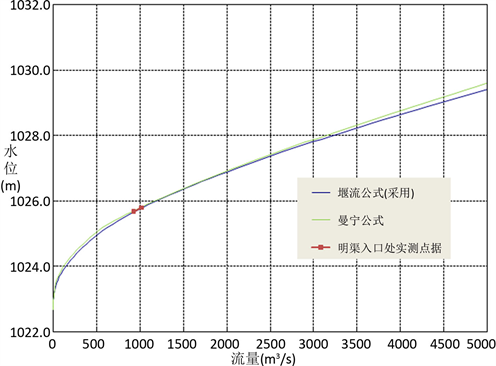
Figure 2. The flow-rating curve in DM2 section
图2. DM2断面水位流量关系曲线
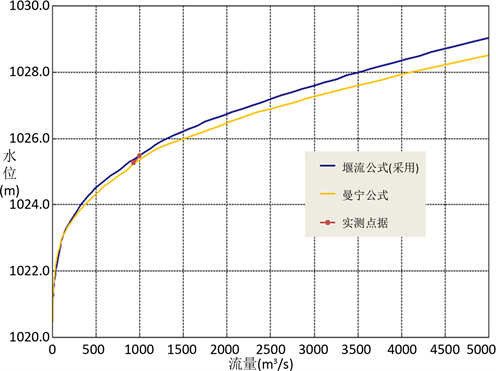
Figure 3. The flow-rating curve in DM4 section
图3. DM4断面水位流量关系曲线
3.3.4. 水位流量关系曲线成果选用
从图2可以看出,用曼宁公式和堰流公式所作出的导流明渠入口(DM2)水位流量关系曲线较为贴合,且都与实测点据拟合较好,能较好地反应出此处河道的过流形态。堰流公式成果略偏安全,推荐采用。
从图3可以看出,用曼宁公式和堰流公式所作出的坝址(DM4)水位流量关系均与实测点据拟合较好,但两条曲线在中高水部分逐渐分离,堰流公式水位略高于曼宁公式。DM4下游约30 m为一处落差约5 m的瀑布,DM4处水流流态受瀑布影响明显,从河道现场情况与水力学方法的符合性和工程安全性考虑,推荐采用堰流公式成果。
3.4. 水位流量关系曲线成果的验证与修订
上述方法只是在水电工程规划设计前期,基础资料较为匮乏情况下的一种相对合理的理论性方法,其在参数选取等环节均存在一定的主观性和理论性,得出的成果也缺乏实际资料进行验证。在U国的K水电项目中,随着项目的推进,勘测设计单位在工程特征点位处设立了水尺并进行流量观测。根据累积的实测水位、流量数据对利用水力学方法计算得出的水位流量关系曲线进行验证后发现,水位流量关系曲线的中水部分基本通过了实测点群,精度尚可;高水部分略低于实测点据,对此部分成果进行了抬高修正 [12]。
4. 结论与建议
1) 测量河道断面不等于有效过水断面 [13]。河道断面面积一般由外业测量人员根据测量任务书中标示位置测得,但受作业条件限制,工程特征断面处及其下游临近范围内河道中如沙洲、巨石、小岛等的地形往往不能完整的测到。因此,水文专业人员在确定断面有效过流面积时,还应扣除上述不过水部分面积 [14]。如是弯道河段,还应扣除凹岸边滩不过水区域面积。此外还应根据工程河段的纵断面图来判断工程特征点位处河段是否为深潭河段。若是,还应扣除深潭下部的不过流死水部分面积。
2) 过水断面糙率n应由行洪区域水流流态、河床质特征以及下垫面等条件综合分析确定。一般来说,河道中泓区域糙率较小,河床质光滑、植被稀疏区域糙率较小;反之,滩地区域、植被密集且高低起伏的行洪区域糙率则较大。河道低水部分的糙率大于中、高水部分的糙率,并在中高水部分最终趋于某一稳定值。
3) 水力学比降应不同流量级比较后综合选用。一般河道在低、中、高水时,其水面比降是不尽相同。在实际设计中,若缺乏不同流量等级的水面线测量成果作为计算依据,一般可采用测时水面线比降作为水位流量关系曲线低、中水部分的水面比降,历史洪痕所得的比降可作为高水部分的水面比降,低、中、高水部分的水面比降应考虑合理过渡。
4) 流量系数应结合实测率定值与查手册推荐值后综合选用。对于复杂山区性河道,中低水时一般较小,且有时还受淹没出流的影响,水位流量关系曲线相对较为陡峭。高水时一般流量系数较大,水位流量关系曲线相对较为平缓。流量系数的确定应主要依靠实测水位流量点据率定得到。水力学手册中天然规整明渠的流量系数取值推荐范围只宜作为参考。
5) 恒定流方法的误差可控。关于恒定流方程推求各断面测时水面线及其所对应流量可能有较大误差的疑虑,不能以水库回水末端上游河道的水位不受水库回水影响的常识加以消除。图4所示水面线为某工程设计的实例。由图4可见,起始断面水位即便是相差1 m的情况下,上游设计断面的水位仍保持稳定,只是在起始边界附近略有差别,这说明只要起始断面距离工程设计断面有一定的间隔,起始断面边界条件的一定误差不会影响到工程设计断面成果可靠性。
6) 实测数据最可靠。前文所述利用曼宁公式、堰流公式和MIKE 11水动力学模型等方法计算水电工程特征断面水位流量关系曲线,虽然根据笔者自身工程经验认为其精度在工程前期可接受,但对于工程投资较大、一旦失事后影响巨大的水电工程来讲并不够严谨。因此,在实际设计中利用本文提到的相关方法分析计算水位流

Figure 4. Schematic diagram of the effect of different initial water levels on water surface curve
图4. 不同起始水位对水面线成果影响示意图
量关系曲线时,还应尽早尽快开展水文外业工作,对工程特征断面河道进行水位流量观测,以便对现有成果进行及时的验证和修订。
基金项目
中国电力建设股份有限公司项目(DJ-ZDZX-2016-02)。
文章引用
张发鸿,岳青华,郭 靖. 缺乏水文资料的复杂天然河道断面水位流量关系曲线计算
Calculation of Rating Curve at Cross Section in Complex Natural River with Few Hydrology Data[J]. 水资源研究, 2020, 09(03): 320-328. https://doi.org/10.12677/JWRR.2020.93033
参考文献
- 1. 范可旭, 伍宁. 拟定坝址水位流量关系的水力学方法[J]. 人民长江, 1999, 30(3): 30-31. FAN Kening, WU Ning. Hydrualic method of rating curve plotting at dam site. Yangtze River, 1999, 30(3): 30-31. (in Chi-nese)
- 2. 王文英, 李百克, 邹文安. 曼宁公式在工程水文设计中的应用[J]. 东北水利水电, 2010, 28(5): 13-15. WANG Wenyin, LI Baike, and ZOU Wenan. The application of Manning Formula in engineering hydrology design. Water Resources & Hydropower of Northeast China, 2010, 28(5): 13-15. (in Chinese)
- 3. KIM, D., YANG, S. K. Analysis of loop-rating curve in a gravel and rock-bed mountain stream. South Korea’s Water Resources, 2012, 45(9): 853-860. https://doi.org/10.3741/jkwra.2012.45.9.853
- 4. 王洪贵, 崔连贞. 确定水位流量关系曲线的一般性分析[J]. 海河水利, 2001(5): 15-16. WANG Honggui, CUI Lianzhen. Normal analysis on decision of rating curve. Haihe Water Resources, 2001(5): 15-16. (in Chinese)
- 5. 梅立庚. 水力学法在水位流量关系拟定中的应用[J]. 海河水利, 2006(6): 47-48. MEI Ligeng. Application of hydraulic method in plotting of rating curve. Haihe Water Resources, 2006(6): 47-48. (in Chi-nese)
- 6. US ARMY CORPS OF ENGINEERS HYDROLOGIC ENGINEERING CENTER. HEC-RAS river analysis sys-tem hydraulic reference manual version. Davis, CA: U.S. Army Corps of Engineers Institute for Water Resources Hydrologic Engineering Center, 2010. https://doi.org/10.21236/ada204560
- 7. 徐俊. 探析水位流量关系对水电工程设计的主要影响[J]. 西北水电, 2014(2): 8-12. XU Jun. Analysis of major impacts on hydropower project design by stage-discharge relationship. Xibei Hydropower, 2014(2): 8-12. (in Chinese)
- 8. 宋运凯, 张丹丹, 田长涛. 水位流量关系曲线拟合方法实例分析[J]. 黑龙江水利科技, 2010, 38(2): 51-52. SONG Yunkai, ZHANG Dandan, and TIAN Changtao. Example analysis on plotting method of rating curve. Heilongjiang Science and Technology of Water Conservancy, 2010, 38(2): 51-52. (in Chinese)
- 9. 茹建辉. 河道水位流量关系曲线和水面线的设计计算——工程水力学几个问题之二[J]. 广东水利水电, 2008(1): 1-7. RU Jianhui. Design and alculation on rating curve and water level of river channel—Several problem on engineering hydraulic of 2nd. Guangdong Water Resources and Hydropower, 2008(1): 1-7. (in Chinese)
- 10. 门玉丽, 夏军, 叶爱中. 水位流量关系曲线的理论求解研究[J]. 水文, 2009, 29(1): 1-3. MEN Yulin, XIA Jun, and YE Aizhong. Theoretical equation of stage-discharge relation curve. Journal of China Hydrology, 2009, 29(1): 1-7. (in Chinese)
- 11. BHATTACHARYA, B., SOLOMATINE, D. P. Neural network and M5 model trees in modelling water level-discharge relationship. Neurocomputing, 2005, 63: 381-396. https://doi.org/10.1016/j.neucom.2004.04.016
- 12. 程银才, 范世香. 水位流量关系曲线高水延长方法新探讨[J]. 水电能源科学, 2011, 29(7): 8-9. CHENG Yincai, FAN Shixiang. Discussion on extending of high water level for discharge rating curve. Water Resources and Power, 2011, 29(7): 8-9. (in Chinese)
- 13. KNIGHT, D. W., HAMED, M. E. Boundary shear in symmetrical compound channels. Journal of Hydraulics Engineering, 1984, 110(10): 1412-1430. https://doi.org/10.1061/(asce)0733-9429(1984)110:10(1412)
- 14. 胡鹏, 崔小红, 等. 流域水文模型中河道断面概化的原理和方法[J]. 水文, 2010, 30(5): 38-41. HU Peng, CUI Xiaohong, et al. Principle and method of river cross section regularization in watershed hydrological model. Journal of China Hydrology, 2010, 30(5): 38-41. (in Chinese)
