Geographical Science Research
Vol.
08
No.
04
(
2019
), Article ID:
33120
,
7
pages
10.12677/GSER.2019.84038
Analysis of Evaporation Complementary Relationship in Semi-Arid Areas
Ziyu Liu
School of Atmospheric Sciences, Chengdu University of Information Technology, Chengdu Sichuan
Received: Nov. 1st, 2019; accepted: Nov. 18th, 2019; published: Nov. 25th, 2019

ABSTRACT
Using the net radiation, latent heat flux, average wind speed, average temperature and average relative humidity data of Yuzhong County from 2006 to 2009, the effects of meteorological factors on actual evapotranspiration, possible evapotranspiration and wet evapotranspiration were studied and the relative actual evapotranspiration was used. An estimated model of the actual evapotranspiration is established relative to the possible evapotranspiration. The study found that in the course of daily changes, the actual evapotranspiration, possible evapotranspiration, and evapotranspiration in the humid environment showed a trend of increasing first and then decreasing. There is an important influence on the actual evapotranspiration. The meteorological factor is the near-surface temperature, showing a negative correlation. The main influencing factor of the evapotranspiration in the humid environment is the meteorological factor of ground net radiation, showing a positive correlation. An estimation model of the actual evapotranspiration (A = 0.834, B = −0.664) was further established, and the model was proved to have practical availability.
Keywords:Possible Evapotranspiration, Wet Evapotranspiration, Actual Evapotranspiration Estimation Model
半干旱地区蒸发互补关系
刘子瑜
成都信息工程大学大气科学学院,四川 成都
收稿日期:2019年11月1日;录用日期:2019年11月18日;发布日期:2019年11月25日

摘 要
利用榆中县2006~2009年净辐射、潜热通量、平均风速、平均温度、平均相对湿度资料研究气象因子对实际蒸散量、可能蒸散量和湿润环境蒸散量的影响并利用相对实际蒸散量与相对可能蒸散量建立起实际蒸散量的估算模型。研究发现,在日变化过程中,实际蒸散量、可能蒸散量以及湿润环境蒸散量呈现出先升高、后下降的日变化特征。对实际蒸散量有重要影响的气象因子是近地层温度,呈现负相关关系,湿润环境蒸散量主要的影响因素是地面净辐射这一气象因子,呈现出正相关关系。进一步建立起实际蒸散量的估算模型(A = 0.834, B = −0.664),并通过检验证明该模型具有实际可用性。
关键词 :可能蒸散量,湿润环境蒸散量,实际蒸散量估算模型

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
近世纪以来,水资源问题对全人类生活的影响早已逐渐成为国际最重要的议题之一。它对人类所生存的全球环境和国际的经济发展的影响是潜移默化的。随着对气候变化的研究逐渐重视,研究在水文循环中占有核心一环的蒸散发过程就显的尤为重要。蒸散发过程不仅是水文循环中的关键一环,更是在大气–土壤中充当“桥梁”的作用。
蒸散发(Evapotranspiration, ET)是由陆面表层蒸发和植物表面水分蒸发所构成的连续过程 [1],关于蒸散发的研究已经有200多年的历史,国内外学者对此进行大量的研究,建立了区域蒸散发相关关系的互补关系模型 [2];并发现3种实际蒸散量模型对不同气候地区有不同的适用性 [3];建立了高原上的蒸发悖论 [4] 和Bouchet互补相关假设 [5];此外,研究发现植被生长季内的年平均降水量与潜在蒸散量之间存在一定差值 [6],各气象因素与蒸散量也有一定相关关系 [7];另外,研究发现陆地上主要的淡水资源来源于降水,而蒸散发过程与降水息息相关,且地表热量的平衡状态水分收支的平衡状态,地理气候环境形成和演变的关键因素也是蒸散发过程 [8]。
榆中县地处甘肃省中部、省会兰州东郊,总面积3301.64平方公里。海拔在1480~3670米之间,据国家气象局统计,榆中年均降雨量与蒸发量相差较大,降水量在350毫米左右,蒸散量远大于降水量在1450毫米左右,总统计得年平均气温在6.7℃左右。总的来说,榆中的气候属温带半干旱气候区,由于受地理条件影响,榆中大陆性季风气候比较明显。因此,研究榆中地区蒸散发过程有重要意义。
2. 资料和方法
2.1. 资料
气象要素数据包括净辐射,潜热通量,平均风速,平均温度,平均相对湿度。该数据来源于榆中县气象台得到的基本气象观测资料。
2.2. 方法
计算可能蒸散量( )以及湿润环境蒸散量( )时选取Morton [9],Davies [10],Brutsaert [11] [12] 的等定义的Penman ( ),Priestley-Taylor ( )公式: ,。
采用相关分析法研究气象因子对实际蒸散量和湿润环境蒸散量的影响 [13] [14] [15]。相关分析是研究两个或两个以上处于同等地位的随机变量间的相关关系的统计分析方法,相关系数计算公式如下所示
(1)
其中 和 分别表示第k,第l个变量的标准差, 的绝对数值越大,表示两者的关系越密切。
3. 结果和分析
3.1. 蒸散量日变化特征分析
如图1所见,可能蒸散量,实际蒸散量,和湿润环境蒸散量总的走向在一天之中的变化趋势相同,从凌晨至下午一直为增长趋势,在15时左右达到峰值。自下午后又开始呈现下降趋势。实际蒸散量主要取决于潜热通量,随潜热通量的增长(或降低),而增长(或降低)。20时左右,实际蒸散量出现一个明显较大的增长起伏,可能是与当地当晚的降水情况、土壤湿润度、以及大气干燥度有关。而湿润环境蒸散量则主要与当天的净辐射有关,日出前,来自太阳的短波辐射小于地表辐射出去的长波辐射时,净辐射为负,使得湿润环境蒸散量较小,日出后,随着地面接收到的太阳短波辐射增强,湿润环境蒸散量也会随之增加,直到当太阳辐射不再大于地面所放射出的长波辐射时,其会随之减少。

Figure 1. Diurnal variation of actual evapotranspiration ( ), possible evapotranspiration ( ) and wet evapotranspiration ( )
图1. 实际蒸散量( ),可能蒸散量( )以及湿润环境蒸散量( )的日变化图
3.2. 实际蒸散量湿润环境蒸散量与气象因子的关系
影响区域的实际蒸散发的因素众多,机理较为复杂。进一步利用地面净辐射(Rn)、潜热通量(LE)、风(U)、平均温度(T)以及相对湿度(H)这五个气象要素来探究对气象因子对实际蒸散量及湿润环境蒸散量的影响。由实际蒸散量与各气象因子的相关关系(图2)可以得到。
实际蒸散量随地面净辐射的变化呈现正相关的关系,相关系数为0.127,在置信度为0.01时,正相关性是显著的;实际蒸散量随风速的变化呈负相关,相关系数为0.484,同样在置信度为0.01时负相关显著;实际蒸散量与温度也呈负相关,相关系数为0.533,在置信度为0.01时负相关关系显著;实际蒸散量随相对湿度变化呈正相关,相关系数为0.32,置信度为0.01时负相关关系显著。因此,温度与实际蒸散量的相关关系最大,可认为本文影响实际蒸散发的主要是近地层温度这一气象因子。

Figure 2. Correlation between actual evapotranspiration and Rn, U, T, H
图2. 实际蒸散量与Rn、U、T、H的相关关系
由图3可以看出,在置信度为0.01时,湿润环境蒸散量与地面净辐射呈现出正相关关系,相关系数为0.928,正相关性显著;湿润环境蒸散量随风速的变化呈正相关,相关系数为0.224,在置信度为0.01时,正相关关系是显著的;湿润环境蒸散量与温度呈正相关,相关系数为0.567,置信度为0.01时,正相关关系显著;湿润环境蒸散量随相对湿度的变化呈现出负相关的关系,相关关系为0.644,在置信度为0.01时,相关性显著。由上述相关性分析表明,在可信的置信度下,湿润环境蒸散量与地面净辐射的相关系数最大。由此,可以认为相比于风速、温度以及相对湿度,使湿润环境蒸散量改变得主要原因是来自于地面的净辐射。综合来看,对实际蒸散量、湿润环境蒸散量的影响因素分别是近地层温度和地面的净辐射这两个气象因子。
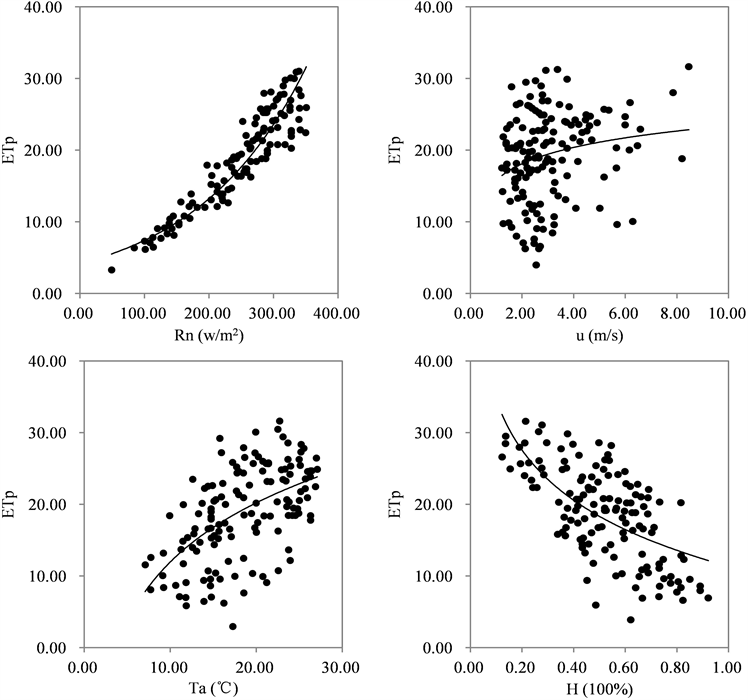
Figure 3. Correlation between evapotranspiration and Rn, U, T and H in humid environment
图3. 湿润环境蒸散量与Rn、U、T、H的相关关系
3.3. 实际蒸散量的估算模型建立
本文选择Morton,Davies,Brutsaert的等定义的Penman,Priestley-Taylor估算式,用 表示相对实际蒸散,用 表示相对可能蒸散,建立一线性的回归模型。如相对实际蒸散、相对可能蒸散拟合的效果图(图4)所示,其中,线性回归方程参数估计值 ,。相对实际蒸散量和相对可能蒸散量的相关性为负,但并不是完全负相关,建立线性回归方程为 带入上述 、 以及 的估算式可得:
(2)
其中, 为饱和水汽压曲线斜率(KPa/℃)、 为干湿常数(KPa/℃);G为土壤热通量(MJ/(m2∙d))、 为净辐射(W/m2), 是关于风速函数和相对湿度的量,带入参数可得半干旱地区的日际实际蒸散量估算的模型:
(3)
这里建立的实际蒸散量的估算模型,是日际估算模式,由于 、 以及 的估算式选取不同,也会出现一定的误差。进一步验证模型,用2006年的实际蒸散量 与使用估算的模型所得到的估算实际蒸散量 进行对比,用 和 的相关关系验证所建立日际实际蒸散量模型的精确度,如图4可见,实际蒸散量( )与估算实际蒸散量( )呈现线性回归关系,相关系数为0.941,均方根误差RMSE = 0.434,因此本文建立半干旱地区的估算日际实际蒸散量的模型有一定的实际可用性。
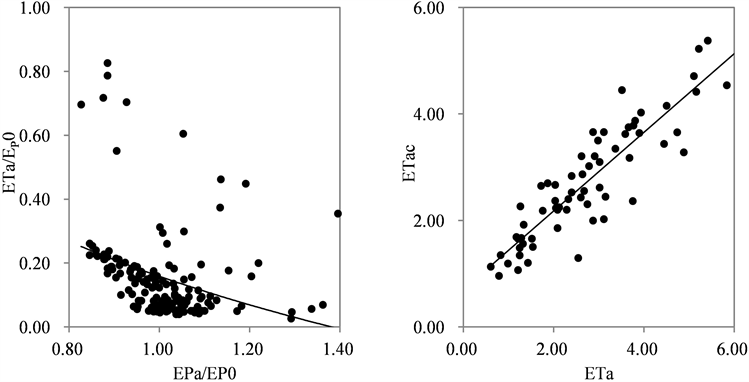
Figure 4. Correlation diagram between the actual evapotranspiration and the relative evapotranspiration, the actual evapotranspiration and the estimated actual evapotranspiration
图4. 相对实际蒸散与相对可能蒸散的拟合图、实际蒸散量和估算实际蒸散量的相关关系图
4. 结论
1) 在日变化的过程中,受地面所接受净辐射、潜热通量、空气湿度、温度等因素的影响,实际蒸散量、可能蒸散量以及湿润环境蒸散量随陆面热量的增加和温度的升高呈现出先升高、后下降的日变化特征。可能蒸散量在先上升后下降的基础上,一直大于实际蒸散量和湿润环境蒸散量。
2) 根据各气象因子与实际蒸散量和湿润环境蒸散量的相关性分析,可以得到,潜热通量是影响实际蒸散量的主要气象因子,呈现负相关关系,相关系数为0.533,地面净辐射是影响湿润环境蒸散量的主要气象因子,在置信度为0.01下正相关性显著,相关系数为0.928。
3) 利用相对实际蒸散量和相对可能蒸散量建立起实际蒸散量的估算模型
,并检验所得实际蒸散量估算式精确度,得到实际蒸散量与估算蒸散量的相关系数为0.941,均方根误差RMSE = 0.434,故该模型通过检验。
基金项目
成都信息工程大学本科教学工程项目(BKJX2019007,BKJX2019013,BKJX2019042,BKJX2019056,BKJX2019062,BKJX2019081,BKJX2019089,BKJX2019120和JY2018012)支持。
文章引用
刘子瑜. 半干旱地区蒸发互补关系
Analysis of Evaporation Complementary Relationship in Semi-Arid Areas[J]. 地理科学研究, 2019, 08(04): 363-369. https://doi.org/10.12677/GSER.2019.84038
参考文献
- 1. 刘建梅, 王安志, 刁一伟, 等. 分布式模型在流域蒸散模拟中的应用与验证[J]. 应用生态学报, 2006, 17(1): 16-24.
- 2. 冯国章. 区域蒸散发量的气候学计算方法[J]. 水文, 1994(3): 7-11+65.
- 3. 韩松俊, 胡和平, 田富强. 三种通过常规气象变量估算实际蒸散量模型的适用性比较[J]. 水利学报, 2009, 40(1): 75-81.
- 4. 谢平, 陈晓宏, 王兆礼, 等. 东江流域实际蒸发量与蒸发皿蒸发量的对比分析[J]. 地理学报, 2009, 64(3): 270-277.
- 5. 李鹏飞, 孙小明, 赵昕奕. 近50年中国干旱半干旱地区降水量与潜在蒸散量分析[J]. 干旱区资源与环境, 2012, 26(7): 57-63.
- 6. Zhang, Y., Liu, C., Tang, Y., et al. (2007) Trends in Pan Evaporation and Reference and Actual Evapotranspiration across the Tibetan Plateau. Journal of Geophysical Research, 112, D12110.
https://doi.org/10.1029/2006JD008161 - 7. Thornthwaite, C.W. (1948) An Approach toward a Rational Classi-fication of Climate. Geographical Review, 38, 55-94.
https://doi.org/10.2307/210739 - 8. Priestley, C.H.B. (1972) On the Assessment of Surface Heat Flux and Evaporation Using Large-Scale Parameters. Monthly Weather Review, 100, 81-92.
https://doi.org/10.1175/1520-0493(1972)100<0081:OTAOSH>2.3.CO;2 - 9. Davies, J.A. and Allen, C.D. (2010) Equilibrium, Potential and Actual Evaporation from Cropped Surfaces in Southern Ontario. Journal of Applied Meteorology, 12, 1312-1321.
- 10. Burutsaert, W. (1979) An Advection Aridity Approach to Estimate Actual Regional Evapotranspiration. Water Resources Research, 15, 443-450.
https://doi.org/10.1029/WR015i002p00443 - 11. 邱新法, 曾燕, 缪启龙, 等. 用常规气象资料计算陆面年实际蒸散量[J]. 中国科学地球科学, 2003, 33(3): 281-288.
- 12. 易诗雅. 《中国国家地理》办刊特征研究[D]: [硕士学位论文]. 长沙: 湖南师范大学, 2014.
- 13. 徐敏, 朱永华, 李源, 等. 淮北平原实际蒸散量计算及时空分布特征分析[J]. 水电能源科学, 2016(1): 10-14.
- 14. 刘钰, Pereira, L.S., Teixeira, J.L., 等. 参照腾发量的新定义及计算方法对比[J]. 水利学报, 1997(6): 27-33.
- 15. 刘昌明, 张丹. 中国地表潜在蒸散发敏感性的时空变化特征分析[J]. 地理学报, 2011, 66(5): 579-588.