Modeling and Simulation
Vol.05 No.04(2016), Article ID:19102,8
pages
10.12677/MOS.2016.54023
Stability and Hopf Bifurcation for an Epidemic Model with B-DA and Delay
Chengyan Qiu1*, Dongwei Huang1#, Yongfeng Guo1, Yong Liu2
1School of Science, Tianjin Polytechnic University, Tianjin
2Key Laboratory of Advanced Textile Composites, Ministry of Education of China, School of Textiles, Tianjin Polytechnic University, Tianjin

Received: Nov. 8th, 2016; accepted: Nov. 26th, 2016; published: Nov. 29th, 2016
Copyright © 2016 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
In this paper, we built an epidemic model with Beddington-DeAngelis and delay. First, we analyzed the associated characteristic equation, and then discussed the stability of the equilibrium. Finally, we determined the stability region of the model. Moreover, we found that when the time delay in the model satisfies a series of conditions, the model undergoes Hopf bifurcations and Hopf-Zero bifurcation. Finally, some numerical simulations and phase diagram are given to satisfied theoretical results.
Keywords:Delay Model, Stability, Hopf Bifurcation, Hopf-Zero Bifurcation

具有B-DA功能项的时滞传染病模型的稳定性 与Hopf分岔的分析
邱成燕1*,黄东卫1#,郭永峰1,刘 雍2
1天津工业大学理学院,天津
2天津工业大学纺织学院,教育部纺织复合材料重点实验室,天津

收稿日期:2016年11月8日;录用日期:2016年11月26日;发布日期:2016年11月29日

摘 要
本文建立了带有Beddington-DeAngelis功能项的时滞传染病模型。对于模型的研究,我首先从模型特征方程的特征根进行研究,其次再分析了模型正平衡点的稳定性,接着确定了该模型的稳定性区域,从而发现当模型中的时滞满足一系列的条件时,模型经历Hopf分岔和Hopf-Zero分岔,最后通过数值模拟验证了理论的正确性。
关键词 :时滞模型,稳定性,Hopf分岔,Hopf-Zero分岔

1. 引言
由病毒和真菌感染人或其他生物体后产生的传染病,可以在人群或其相关的生物种群中引起大面积的传播 [1] 。传染病的传染给人类的健康带来很大的影响,在每年的死亡人口中大约有百分之二十五的人是死于传染病 [2] 。因此,研究传染病模型,并掌握病毒传染及细胞间的相互作用机制是非常有必要的 [3] [4] 。进入20世纪以来,微分方程理论才被广泛的应用于传染病相关问题的动力学模型中 [5] [6] [7] [8] ,并取得了有效的成果。然而,先前学者们建立的模型中,传染病的传染速率呈现线性传染,且传染到发病的过程不考虑时间滞后,这是不符合现实情况的。因此我改进的模型中的传染速率是非线性传染的,并符合Beddington-DeAngelis功能函数,在传染到发病还需要有时间滞后过程,更接近于实际情况。本文通过对改进模型的研究,得到传染病模型出现局部稳定、Hopf分岔以及Hopf-Zero分岔的具体条件,从而了解细胞间的相互作用机制,更好的控制传染病的传播。
2. 模型的建立
对于传染病的研究,在文章 [9] 中,关于传染病模型的数学模型可描述为下面的方程:
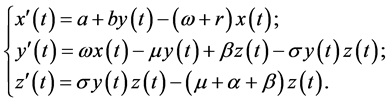 (1)
(1)
其中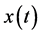 表示未成年个体在t时刻的种群大小,
表示未成年个体在t时刻的种群大小,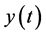 表示成年易感者在t时刻的种群大小,
表示成年易感者在t时刻的种群大小, 表示成年染病者在t时刻的种群大小。
表示成年染病者在t时刻的种群大小。 ,
, ,
,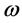 ,
,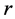 ,
,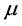 ,
,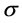 ,
,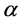 ,
, 都为正常数。
都为正常数。 表示未成年个体到成年个体的转化率,
表示未成年个体到成年个体的转化率, 表示自我康复率,
表示自我康复率, 表示未成年个体的自然死亡率,
表示未成年个体的自然死亡率, 表示成年个体的自然死亡率,
表示成年个体的自然死亡率,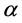 表示因病死亡率,
表示因病死亡率,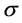 表示单位时间内两个接触个体之间传播疾病的概率。
表示单位时间内两个接触个体之间传播疾病的概率。
本文中我的改进模型如下:
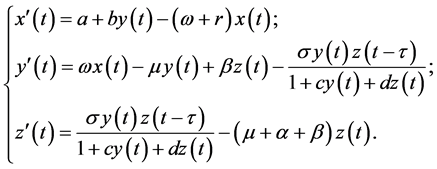 (2)
(2)
其中 是感染到发病的时间,
是感染到发病的时间, 为成年易感者和染病者之间的非线性的Beddington-DeAngelis发生率。
为成年易感者和染病者之间的非线性的Beddington-DeAngelis发生率。
下面本文将从分析系统(2)的稳定性以及系统(2)的分岔两个方面来论述,并借鉴文 [10] [11] [12] [13] [14] 中对这两个问题的分析方法,展开对本文所建立的带有Beddington-DeAngelis功能项的时滞系统(2)的平衡点稳定性、Hopf分岔和Hopf-Zero分岔的存在性的定性分析。
3. 平衡点的稳定性
本节将用微分方程理论,研究本文建立的带有Beddington-DeAngelis功能项的时滞系统(2)的动力学行为。经过计算可求出系统(2)有两个平衡点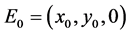 和
和 ,其中,
,其中,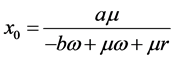 ,
,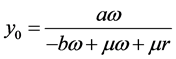 ,
,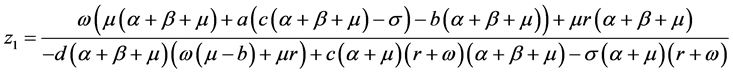

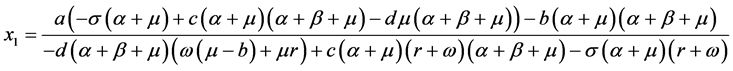 。
。
根据实际意义,我们只讨论平衡点 ,则系统(2)在平衡点
,则系统(2)在平衡点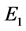 处的雅可比矩阵为
处的雅可比矩阵为
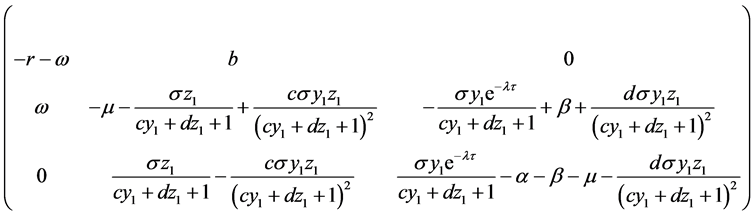
根据雅可比矩阵,则可求出系统(2)在平衡点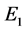 处的特征方程:
处的特征方程:
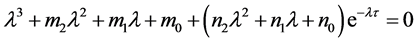 (3)
(3)
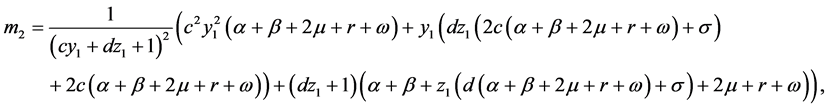
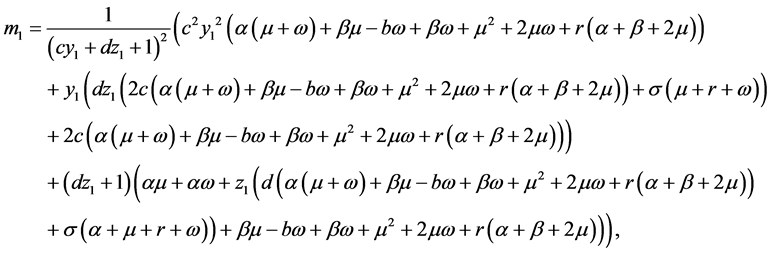

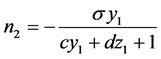 ,
, 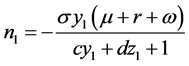 ,
, 
根据赫尔维茨判定定理 [15] 以及微分方程的定性理论,可以得到以下引理:
引理1:(i) 当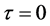 ,
,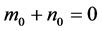 时,此时在
时,此时在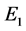 处的特征方程为
处的特征方程为
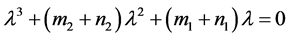 (4)
(4)
显然方程(4)的一个根为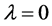 ;当
;当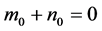 ,
,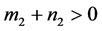 且
且 ,方程(4)有一个零根和两个
,方程(4)有一个零根和两个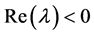 的根,此时系统(2)经历不动点分岔;
的根,此时系统(2)经历不动点分岔;
(ii) 设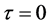 ,如果(H1):
,如果(H1): ,
,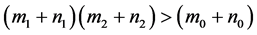 ,
, ,则系统(2)的平衡点在
,则系统(2)的平衡点在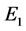 处是渐近稳定的,并且是局部渐近稳定的。
处是渐近稳定的,并且是局部渐近稳定的。
定理1:对于方程 其中
其中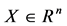 ,
,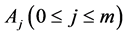 是
是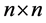 常数矩阵。若特征方
常数矩阵。若特征方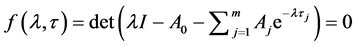 ,
,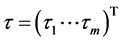 满足下列条件:
满足下列条件:
(i) 方程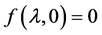 都有负实部的根;
都有负实部的根;
(ii) ,
, ,
,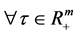 。
。
则方程的所有根具有负实部。
引理2:如果(H1)成立,设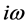 (
(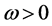 )是方程(3)的根,当
)是方程(3)的根,当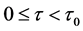 时,则系统(2)的平衡点
时,则系统(2)的平衡点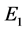 是局部渐近稳定的。这里
是局部渐近稳定的。这里
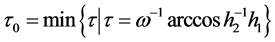 (5)
(5)
其中,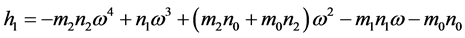 ,
, 。
。
证明:将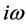 (
(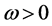 )代入方程(3)并分离实部与虚部可得
)代入方程(3)并分离实部与虚部可得
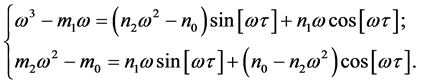 (6)
(6)
从而解得: 。
。
取
 (7)
(7)
由定理1可知,当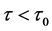 时,特征方程(3)都有
时,特征方程(3)都有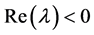 的根,因而系统(2)的平衡点在
的根,因而系统(2)的平衡点在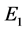 处是局部渐近稳定的。
处是局部渐近稳定的。
4. Hopf分岔的存在性
设方程(3)的根为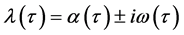 ,且满足
,且满足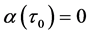 ,
,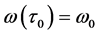 。
。
定理2:如果引理2的条件成立,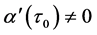 ,那么当
,那么当 时系统(2)在
时系统(2)在 处产生Hopf分岔,
处产生Hopf分岔,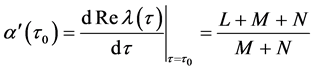 ,其中,
,其中, ,
,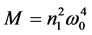 ,
,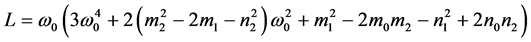 。
。
证明: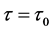 时,特征方程(3)有一对纯虚根,并且其余的根都是
时,特征方程(3)有一对纯虚根,并且其余的根都是 的。将特征方程(3)两边对
的。将特征方程(3)两边对 求导,整理得
求导,整理得 。其中,
。其中,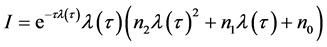
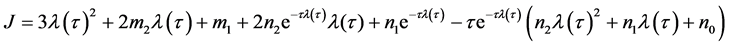
将 带入
带入 ,并且
,并且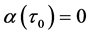 ,
,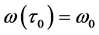 。
。
整理化简得:
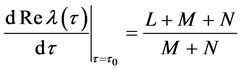
所以,当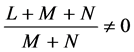 时,系统(2)在
时,系统(2)在 处出现Hopf分岔。
处出现Hopf分岔。
5. Hopf-Zero分岔的存在性分析
下面证明系统(2)存在Hopf-Zero分岔。
将(6)式中的两个方程平方相加,可得将(5)中两个方程平方相加可得
 (8)
(8)
其中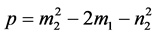 ,
, ,
,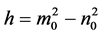 。令
。令 ,则(8)式化为
,则(8)式化为
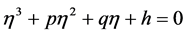 ,记
,记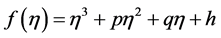 (9)
(9)
引理3:假设条件(H1)及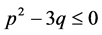 成立,则可得以下结论:
成立,则可得以下结论:
(i) 如果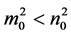 ,则当
,则当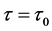 时,方程(3)有一对纯虚根
时,方程(3)有一对纯虚根 ,且当
,且当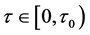 时方程(3)都有
时方程(3)都有 的根,其中
的根,其中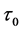 的定义如(7)式。
的定义如(7)式。
(ii) 如果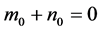 ,
,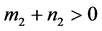 ,
,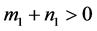 ,则当
,则当 时,方程(3)除了有一个零根外,其余根都是
时,方程(3)除了有一个零根外,其余根都是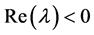 的根。
的根。
证明:(i)用反证法证明。如果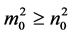 且
且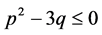 ,则方程(9)没有正实根。由(9)式可得
,则方程(9)没有正实根。由(9)式可得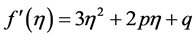 。显然,当
。显然,当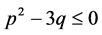 时,函数
时,函数 在
在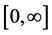 上是单调增加的,所以当
上是单调增加的,所以当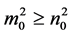 且
且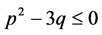 时,方程(9)没有正实根。所以不失一般性,由定理1及根的连续性可知,如果
时,方程(9)没有正实根。所以不失一般性,由定理1及根的连续性可知,如果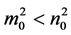 ,则当
,则当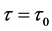 时,方程(3)有一对纯虚根
时,方程(3)有一对纯虚根 ,且当
,且当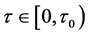 时方程(3)都具有
时方程(3)都具有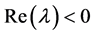 的根,其中
的根,其中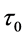 的定义如(7)式。
的定义如(7)式。
(ii) 因为 ,
,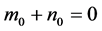 ,显然0是方程(3)的根。由引理2可知,此时方程(3)是没有纯虚根的。
,显然0是方程(3)的根。由引理2可知,此时方程(3)是没有纯虚根的。
下面可以用反证法证明。令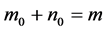 。假设有
。假设有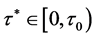 ,方程(3)有
,方程(3)有 的根,记为
的根,记为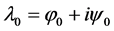 ,记
,记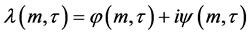 是方程(3)的根,并且满足
是方程(3)的根,并且满足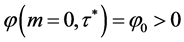 ,
,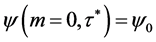 。因为
。因为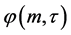 关于
关于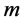 连续,则存在
连续,则存在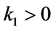 当
当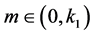 时,
时,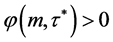 。又因为
。又因为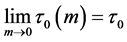 ,有
,有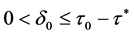 ,存在
,存在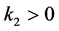 ,如果
,如果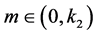 ,则有
,则有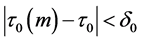 ,从而可得
,从而可得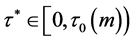 。取
。取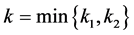 ,当
,当 时,
时,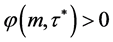 且
且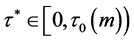 。另一方面,由引理2可知,当
。另一方面,由引理2可知,当 时,方程(3)的根都是
时,方程(3)的根都是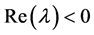 的,矛盾。引理3得证。
的,矛盾。引理3得证。
定理3:如果 ,
,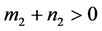 ,
,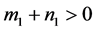 ,那么当
,那么当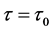 时,方程(3)除了有一个
时,方程(3)除了有一个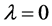 的根和一对纯虚根
的根和一对纯虚根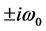 外,其余根都是
外,其余根都是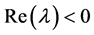 的。此时系统(2)在平衡点
的。此时系统(2)在平衡点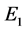 处经历了Hopf-Zero分岔。
处经历了Hopf-Zero分岔。
证明:显然,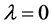 是方程(3)的根,我们由定理2可知,
是方程(3)的根,我们由定理2可知,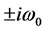 也是方程(3)的根。假设
也是方程(3)的根。假设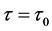 时,使得方程(3)有一个
时,使得方程(3)有一个 的根,记为
的根,记为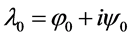 。设
。设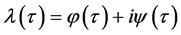 是方程(3)的根,并且满足
是方程(3)的根,并且满足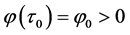 ,
,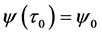 。因此当
。因此当 时,方程(3)有
时,方程(3)有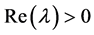 的根,这与引理3矛盾。定理3得证。
的根,这与引理3矛盾。定理3得证。
6. 数值模拟
在系统(2)中取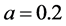 ,
,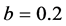 ,
,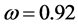 ,
,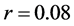 ,
, ,
,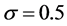 ,
,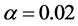 ,
,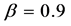 ,
,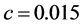 ,
, ,将这些参数代入
,将这些参数代入 ,通过计算可得系统(2)的正平衡点为
,通过计算可得系统(2)的正平衡点为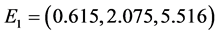 。若满足(H1)和
。若满足(H1)和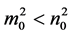 ,则方程(6)有一个正实根
,则方程(6)有一个正实根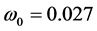 。再由(9)式可得
。再由(9)式可得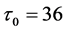 ,
, 。
。
本节主要是对系统(2)通过取不同的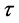 值,来研究Hopf分岔,Hopf-Zero分岔以及周期解的稳定性。图1、图2、图3分别给出了
值,来研究Hopf分岔,Hopf-Zero分岔以及周期解的稳定性。图1、图2、图3分别给出了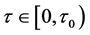 ,
,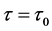 和
和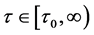 时的时间历程图和相图。
时的时间历程图和相图。
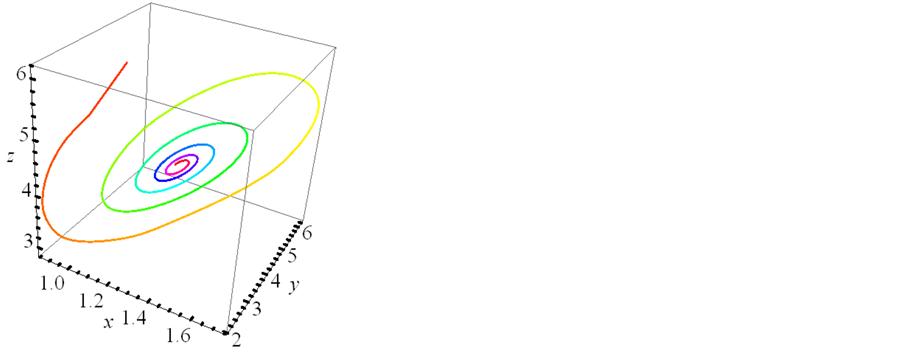
Figure 1. τ = 12, the time-history graph and phase diagram of the system (2)
图1. τ = 12时,系统(2)的时间历程图和相图

Figure 2. τ = 36, the time-history graph and phase diagram of the system (2)
图2. τ = 36时,系统(2)的时间历程图和相图

Figure 3. τ = 55, the time-history graph and phase diagram of the system (2)
图3. τ = 55时,系统(2)的时间历程图和相图
(1) 由图1,可以看出如果病毒感染到发病的周期在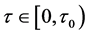 时,
时, ,
,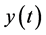 ,
, 随时间的变化最终趋于稳定,此时系统(2)在平衡点
随时间的变化最终趋于稳定,此时系统(2)在平衡点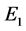 处是局部渐近稳定的,说明该传染病不会大面积爆发,有可能成为地方病。
处是局部渐近稳定的,说明该传染病不会大面积爆发,有可能成为地方病。
(2) 由图2,可以看出如果病毒感染到发病的周期在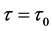 时,
时,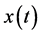 ,
,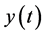 ,
,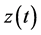 随时间的变化出现周期变化,此时系统出现周期解,系统(2)在平衡点
随时间的变化出现周期变化,此时系统出现周期解,系统(2)在平衡点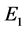 处出现了极限环,并在
处出现了极限环,并在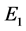 点经历了Hopf分岔,说明该传染病可能会发生周期循环变化。
点经历了Hopf分岔,说明该传染病可能会发生周期循环变化。
(3) 由图3,可以看出如果病毒感染到发病的周期在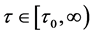 时,系统的相图不稳定,此时系统(2)的平衡点
时,系统的相图不稳定,此时系统(2)的平衡点 是不稳定的,说明该传染病具有敏感性,极小的环境变化都有可能使得该传染病大面积爆发,或者灭绝。
是不稳定的,说明该传染病具有敏感性,极小的环境变化都有可能使得该传染病大面积爆发,或者灭绝。
7. 小结
与先前学者们建立的模型相比,本文建立的模型不仅考虑了病毒传染到发病需要时间过程,并且也考虑了传染的速率呈非线性传染。因此,本文的模型更具有一般性,其动力学性质更能反映传染病的传播规律。文章首先通过讨论系统(2)在正平衡点的稳定性,并以时滞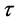 为参数,得出了系统(2)出现Hopf分岔和Hopf-Zero分岔的条件。最后,数值模拟验证了理论的正确性。通过模型图像及理论证明知,当时滞
为参数,得出了系统(2)出现Hopf分岔和Hopf-Zero分岔的条件。最后,数值模拟验证了理论的正确性。通过模型图像及理论证明知,当时滞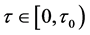 ,系统(2)在正平衡点
,系统(2)在正平衡点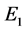 处是渐近稳定的,说明传染病不会大面积的爆发,有可能会成为地方病;当时滞
处是渐近稳定的,说明传染病不会大面积的爆发,有可能会成为地方病;当时滞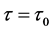 ,系统(2)存在周期解,说明了传染病可能会周期循环变化。
,系统(2)存在周期解,说明了传染病可能会周期循环变化。
基金项目
国家自然科学基金项目(11672207, 51573133, 11501410)。
文章引用
邱成燕,黄东卫,郭永峰,刘雍. 具有B-DA功能项的时滞传染病模型的稳定性与Hopf分岔的分析
Stability and Hopf Bifurcation for an Epidemic Model with B-DA and Delay[J]. 建模与仿真, 2016, 05(04): 183-190. http://dx.doi.org/10.12677/MOS.2016.54023
参考文献 (References)
- 1. 传染病数学模型的研究[M]. 成都: 西南交通大学出版社, 2014.
- 2. 陶龙, 曹磊, 周文, 张道祥. 一类具有时滞传染病模型的Hopf分支分析[J]. 杭州师范大学学报, 2016(1): 81-87.
- 3. 江志超, 曹建涛, 郭照庄. 一类传染病模型的稳定性分析[J]. 大数数学, 2009(4).
- 4. 邹郁松. 我国传染病现状及防治体系建设[J]. 医学研究杂志, 2007, 36(1): 14-18.
- 5. 陈兰荪, 宋新宇, 陆征一. 数学生态学模型与研究方法[M]. 成都: 四川科学技术出版社, 2003.
- 6. 陈兰荪, 孟新柱, 焦建军. 生物动力学[M]. 北京: 科学出版社, 2009.
- 7. Wolinsky, S.M., Kunstman, K.J., Safrit, J.T., et al. (1996) HIV-1 Evolution and Disease Progression. Science, 274, 1010-1011. https://doi.org/10.1126/science.274.5289.1010
- 8. Chan, B.S. and Yu, P. (2012) Bifurcation Analysis in a Model of Cytotoxic T-Lymphocyte Response to Viral Infections. Nonlinear Analysis: Real World Applications, 13, 64-77. https://doi.org/10.1016/j.nonrwa.2011.07.012
- 9. 杨纪华, 赵万霞, 潘霞. 时滞传染病模型的稳定性与分支分析[J]. 宁夏师范学院报, 2015(36): 3.
- 10. 杨纪华, 刘媚. 具时滞倒立摆系统的稳定性与Hopf分支分析[J]. 黑龙江大学自然科学学报, 2014, 31(2): 185- 191.
- 11. Wang, H.B. and Jiang, W.H. (2006) Multiple Stability Analysis in a Magnetic Bearing System with Time Delay. Chaos Solitons and Fractals, 27, 789-799. https://doi.org/10.1016/j.chaos.2005.04.052
- 12. Chaitanya, V.S.K. (2005) Stability Analysis of Structurally Unstable Man-Machine System Involving Time Delays. Nonlinear Analysis: Real Word Applications, 6, 845-857. https://doi.org/10.1016/j.nonrwa.2004.09.006
- 13. Hassard, B.D., Kazarinoff, N.D. and Wan, Y.H. (1981) Theory Applications of Hopf Bifurcation. Cambridge University Press, Cambridge.
- 14. Song, Y.L. and Wei, J.J. (2004) Bifurcation Analysis for Chen’s System with Delayed Feedback and Its Application to Control of Chaos. Chaos Solitons and Fractals, 22, 75-91. https://doi.org/10.1016/j.chaos.2003.12.075
- 15. 马知恩, 周义仓. 常微分方程定性与稳定性方法[M]. 北京: 科学出版社, 2001: 70-71.