Statistics and Application
Vol.
08
No.
06
(
2019
), Article ID:
33307
,
13
pages
10.12677/SA.2019.86103
Measurement of Value at Risk Based on Kernel-Weighted r-Power Variation Estimation of Instantaneous Volatility for Stochastic Diffusion Model
Jiawei Su, Ruixin Wei, Yiyao Liu
School of Mathematics and Statistics, Guangxi Normal University, Guilin Guangxi

Received: Nov. 15th, 2019; accepted: Nov. 28th, 2019; published: Dec. 5th, 2019

ABSTRACT
The risk of financial assets is related to the volatility of return in the financial market. Therefore, when we estimate VaR, which serves as a widely used measurement of assets’ risk, with parametric method, volatility is one of the most important input variables. In this paper, we proposed kernel-weighted estimators of instantaneous volatility with r (r > 0)-power variation for stochastic diffusion model, proving its asymptotic unbiasedness. A simulation study will examine the finite sample properties of the VaR estimated by the estimators we proposed. It is shown that the VaR we estimated passed the test of significance, which means it is reliable to be the measurement of assets’ risk.
Keywords:VaR, Instantaneous Volatility, Stochastic Diffusion Model
基于扩散过程核权r阶幂变差瞬时波动率 估计的VaR度量
苏嘉炜,韦睿心,刘懿瑶
广西师范大学,数学与统计学院,广西 桂林

收稿日期:2019年11月15日;录用日期:2019年11月28日;发布日期:2019年12月5日

摘 要
在金融市场中,收益率序列的波动性往往与金融资产的风险挂钩。因此,VaR作为被普遍认可且有广泛应用的资产风险度量指标,在利用参数法对其进行计算时,波动率是其中重要的输入变量。本文在对数收益率服从随机扩散过程这一假设下,利用r (r > 0)阶幂变差构建瞬时波动率核估计,证明其渐近无偏性,并进一步通过数值模拟来考察由该瞬时波动率估计所计算的VaR在有限样本下的表现。结果显示:在显著性水平为5%的情形下,利用Kupiec检验法对随机扩散过程假设下的VaR结果进行回测检验,所得统计值落在非拒绝域内。由此可见,利用该方法在随机扩散模型下计算出的VaR是可靠的,可用来有效估计资产投资组合的风险。
关键词 :VaR,瞬时波动率,随机扩散模型

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
在金融市场债券,股票和基金等领域,VaR是一项被普遍认可且有广泛应用的风险度量指标,它刻画了在一定置信水平下,投资组合在持有期内的最大潜在损失。该度量方法最早在1994年由Morgan公司提出,随后成为了国际上主流的证券风险度量手段。随着VaR理论的发展,国内外的学者提出了不少有效的测算方法,目前常见的计算方法主要有基于收益率分布假定的参数法,通过历史数据得到模拟结果的非参数法以及基于极值理论的半参数法。数法对VaR进行计算时,关键在于给出合理的模型假定以及该模型下可靠的波动率估计。相较于传统的ARCH/GARCH模型和随机波动(SV)模型,随机扩散模型具有以下两个优点:(1) 模型限制少。该模型只假设资产价格服从布朗运动,而对波动率没有模型上的限制。(2) 适合对连续时间或间隔很短的高频数据作研究。目前已有不少学者提出了随机扩散模型下波动率的许多估计量,Fan [1] (2008)提出了不含市场噪声的瞬时波动率核估计,而之后Kristensen [2] (2010)利用二次幂变差构建了更一般形式的瞬时波动率核估计量。Yacine [3] (2010)提出了在市场微观结构相依噪声影响下的瞬时波动率估计。Sabel [4] (2015)通过小波变换构造了瞬时波动率的估计量。Vatter [5] (2015)用傅里叶变换的方法对含季节变动的瞬时波动率进行估计。蔡井伟 [6] (2017)针对时间相依情形的核估计问题,给出了带有离散观察值的基于两步平滑的瞬时波动率估计量。刘红月 [7] (2017)结合了高频和低频的金融数据,提出了一种瞬时波动率分布的核估计方法。
瞬时波动率的核估计都需要对窗宽进行选择,窗宽的选择会对估计的精准度有较大的影响。而最优窗宽往往包含难以估计的未知参数,这导致在实际应用中常常面临最优窗宽具体取值难以确定的问题。对此,王江涛和周勇 [8] (2018)就已实现波动率核估计窗宽选择的问题,给出了最优窗宽中未知参数的估计量,并证明由此确定的窗宽是最优窗宽的一致估计量。
本文将在Kristensen [2] (2010)提出的二次幂变差瞬时波动率核估计基础上对随机扩散模型下的瞬时波动率估计作进一步研究,利用 次幂变差构建瞬时波动率核估计并证明其弱相合性与渐近无偏性,之后通过数值模拟来考察由该瞬时波动率估计所计算的VaR在有限样本下的表现。结果显示:在显著性水平为5%的情形下,利用Kupiec检验法对随机扩散过程假设下的VaR结果进行回测检验,所得统计值落在非拒绝域内。由此可见,在随机扩散模型下计算出的VaR是可靠的,可用来有效估计资产投资组合风险。
2. 基本原理和假设
2.1. 模型设定及估计量的定义
本文在资产价格 扩散模型
(2.1)
的基础上利用 次幂变差构建r次幂瞬时波动率核估计
(2.2)
其中 ,,。
2.2. 基本假设
本文理论推导基于以下假设:
(A1) 过程 和 都与过程 独立,且在 上可积和有界。
(A2) 存在 ,使得对于任意 和 ,有
(A3) (i) 核函数K(u)是有界概率密度函数。对于λ > 0,有 。(ii) 存在 ,使得对于任意 ,有
(A4) 当
时,有
,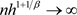 。
。
为方便证明,现给出相关符号的理论推导。由(2.1),我们知道
(2.3)
令
(2.4)
(2.5)
那么有
(2.6)
以及
(2.7)
显然, 包含游离项,而 则不包含游离项。在后续证明中,我们会证明两者的偏差几乎处处收敛于0。
此外,留意到
(2.8)
其中 是相互独立且都服从标准正态分布的随机变量,且都与过程 独立。令
(2.9)
那么有
(2.10)
3. 估计量的渐近无偏性
Theorem 1 在条件(A1)~(A4)同时满足的情况下,有
(3.1)
证明 由引理6.4可知
(3.2)
所以只需证 收敛到零。
记
(3.3)
和
(3.4)
则有
(3.5)
由引理6.3和条件(A2)可知
(3.6)
另一方面,由于
(3.7)
所以
(3.8)
因此,根据条件(A2),我们有
(3.9)
即
(3.10)
从而
(3.11)
联立(3.2)和(3.11),结论证得。
4. 数值模拟
4.1. 数据的选取
本文数值模拟工作基于以下模型:
(4.1)
(4.2)
其中 和 是相互独立的标准布朗运动,参数分别取 , 和 。
在实际模拟中,我们采用以下离散模型:
(4.3)
(4.4)
并假设游离项 ,以及观测时长为 天,其中 和 , 是离散化的步长。
具体操作步骤如下:
(1) 依据离散模型(4.4)获取真值 。因离散模型(4.4)在提取间隔尽可能小的时候才会近似于连续模型(4.2),所以在离散模型(4.4)中我们取时间间隔 ,其中 。
(2) 依据离散模型(4.3)以20秒为提取间隔来产生样本 。离散模型(4.3)中与20秒提取间隔对应的抽样频率为 。
(3) 选取核函数和窗宽。本文选用高斯核来作为核估计中的核函数,而窗宽则依照无偏最小平方交叉实证法来选取。
(4) 取 ,根据公式
(4.5)
产生对应时刻 的瞬时波动率核估计序列 。
4.2. 数据的基本统计特征及正态性检验
表1为对数收益率序列的基本统计量,从表看出序列均值在0附近;偏度系数近乎为0,峰度系数约为3,符合正态分布的特征;J-B统计量的值较小,而p值却很大,说明无法拒绝原假设,序列服从正态分布。
图1为对数收益率序列Q-Q图,图中的样本线与理论线几乎重合,由此进一步从直观上验证了序列服从正态分布。
Table 1. Basic statistics of the log-return
表1. 对数收益率基本统计量
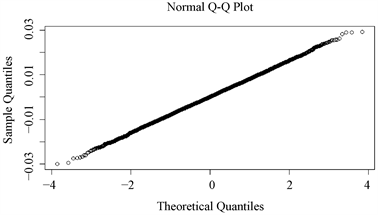
Figure 1. Q-Q plot of the log-return sequence
图1. 对数收益率序列Q-Q图
4.3. 数据的平稳性检验
在实际分析中,往往需要保证对数收益率序列
具有平稳性,即对于任意
,都有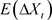 ,
为常数;对于任意
,协方差
只与时间间隔
有关。从图2可以看出对数收益率围绕0上下波动,无明显的趋势特征,而不同时刻的波动大小也没有太大区别,由此从直观上初步判断序列平稳。为了进一步验证这个想法,本文接下来采用ADF单位根检验的方法来判
,
为常数;对于任意
,协方差
只与时间间隔
有关。从图2可以看出对数收益率围绕0上下波动,无明显的趋势特征,而不同时刻的波动大小也没有太大区别,由此从直观上初步判断序列平稳。为了进一步验证这个想法,本文接下来采用ADF单位根检验的方法来判
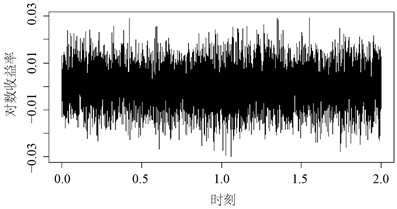
Figure 2. Sequence diagram of the log-return
图2. 对数收益率时序图
断序列的平稳性。
从表2可以看出,检验概率p值为0.01,所以拒绝原假设,认为序列平稳。
Table 2. ADF test result of the log-return based on simulated data
表2. 模拟数据对数收益率ADF检验结果
4.4. 数据的自相关性检验
为确保对数收益率序列满足随机游走假设,下面对模拟数据对数收益率序列作相关性检验,自相关图与偏自相关图如图3和图4所示。
从图3和图4可见,无论是自相关系数还是偏自相关系数,绝大部分均在两倍标准差范围内,可以认为没有显著的相关性。
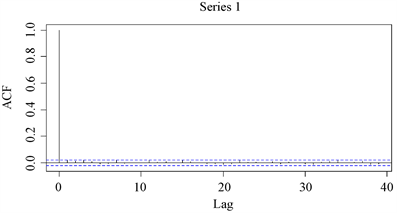
Figure 3. Autocorrelogram of the log-return based on simulated data
图3. 模拟数据对数收益率自相关图
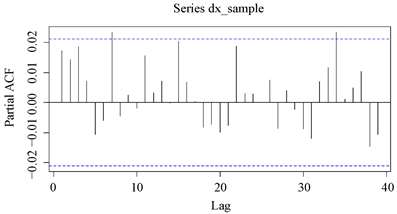
Figure 4. Partial autocorrelogram of the log-return based on simulated data
图4. 模拟数据对数收益率偏自相关图
4.5. 数据的异方差检验
为了检验序列是否存在异方差性,本文采用ARCH-LM检验法来对其进行分析,为此提出的原假设为“序列不存在ARCH效应”,即不存在异方差性及自相关性。
从表3可知,卡方统计量p值大于0.05,所以在5%的显著性水平下,无法拒绝原假设,认为序列不存在异方差性。
Table 3. ARCH-LM test result of the log-return based on simulated data
表3. 模拟数据对数收益率ARCH-LM检验结果
4.6. VaR的定义及计算
VaR通常可理解为“给定某置信水平,投资组合在一定持有期内的最大损失”。设 为投资组合在时刻 时的对数价格,则该投资组合在持有期 内的收益率为
(4.6)
在随机扩散模型下,根据 ,利用参数法对VaR进行计算,其定义的公式如下
(4.7)
其中 为资产初期价值,在后面模拟章节中,我们将其设定为1; 为标准正态分布的 分位数, 为波动率。由此可见,计算VaR的关键是对参数 进行估计。
利用对数收益率序列 ,可计算出在时刻 上的r次幂瞬时波动率估计值
(4.8)
取 ,将估计值 代入(4.7)中,即可得到 序列
(4.9)
在显著性水平为5%的情形下,由此计算得到的VaR值各统计量如表4所示。
Table 4. Statistics of the VaR
表4. VaR统计量
4.7. VaR的有效性检验
为了度量在随机扩散模型下利用核权r阶幂变差瞬时波动率估计所计算的VaR有效性,本文采用Kupiec失败频率检验法。
构造LR统计量:
(4.10)
其中 为显著性水平, ,T为VaR值的个数,N为VaR失效的个数,即实际损失值大于VaR的个数。
在显著性水平为5%的情况下将数据代入相关公式进行计算,得到检验结果如下。
由表5可知,LR统计量为3.0781,小于 的5%分位数3.48,所以无法拒绝原假设,认为在随机扩散模型下由核权r阶幂变差瞬时波动率估计所计算得到的VaR是有效且可靠的。
Table 5. The result of the Kupiec test under the significance level of 5%
表5. 显著性水平5%下的Kupiec失败率检验结果
5. 结论
为了计算证券投资组合风险度量指标VaR,本文在Kristensen [2] (2010)提出的二次幂变差瞬时波动率核估计的基础上,利用 阶幂变差构建了在随机扩散模型假定下的r次幂瞬时波动率核估计量,在合理的假设条件下证明其渐近无偏性。之后通过数值模拟考察由该估计量所计算的VaR值在有限样本下的性质。在Kupiec失败频率检验中,似然统计值LR小于 的5%分位数,这表明:在显著性水平为5%的情形下,利用Kupiec检验法对随机扩散过程假设下的VaR结果进行回测检验,所得统计值落在非拒绝域内。由此可见,利用该方法在随机扩散模型下计算出的VaR是可靠的,可用来有效估计资产投资组合的风险。
基金项目
国家自然科学基金(11461009);广西研究生教育创新项目(XYCSZ2017075)。
文章引用
苏嘉炜,韦睿心,刘懿瑶. 基于扩散过程核权r阶幂变差瞬时波动率估计的VaR度量
Measurement of Value at Risk Based on Kernel-Weighted r-Power Variation Estimation of Instantaneous Volatility for Stochastic Diffusion Model[J]. 统计学与应用, 2019, 08(06): 909-921. https://doi.org/10.12677/SA.2019.86103
参考文献
- 1. Fan, J.Q. and Wang, Y.Z. (2008) Spot Volatility Estimation for High-Frequency Data. Statistics and Its Interface, 1, 279-288. https://doi.org/10.4310/SII.2008.v1.n2.a5
- 2. Kristensen, D. (2010) Nonparametric Filtering of the Realized Spot Volatility: A Kernel Based Approach. Econometric Theory, 26, 60-93. https://doi.org/10.1017/S0266466609090616
- 3. Ait-Sahalia, Y., Mykland, P.A. and Zhang, L. (2010) Ultra High Frequency Volatility Estimation with Dependent Microstructure Noise. Journal of Econometrics, 160, 160-175. https://doi.org/10.1016/j.jeconom.2010.03.028
- 4. Sabel, T., Schmidt-Hieber, J. and Munk, A. (2015) Spot Volatility Estimation for High-Frequency Data: Adaptive Estimation in Practice. In: Modelling and Stochastic Learning for Forecasting in High Dimensions, 213-241. https://doi.org/10.1007/978-3-319-18732-7_12
- 5. Vatter, T., Wu, H., Chavezdemoulin, V. and Yu, B. (2015) Non-Parametric Estimation of Intraday Spot Volatility: Disentangling Instantaneous Trend and Seasonality. Econometrics, 3, 864-887. https://doi.org/10.3390/econometrics3040864
- 6. 蔡井伟, 陈萍, 梅霞. 基于两步平滑的瞬时波动率非参数估计[J]. 统计与决策, 2017(23): 88-90.
- 7. 刘红月. 基于高频低频数据相结合的瞬时波动率分布估计[D]: [硕士学位论文]. 苏州: 苏州大学, 2017.
- 8. 王江涛, 周勇. 高频数据波动率非参数估计及窗宽选择[J]. 系统工程理论与实践, 2018, 38(10): 2491-2500.
附录
引理及证明
为了得到相关的结论,本文需要利用以下的引理。
Lemma 6.1. 记
(6.1)
和
(6.2)
若条件(A1)满足,那么有
(6.3)
Proof 由条件(A1)和积分中值定理得,存在常数 和 ,使得 以及 ,从而有 。
另一方面,
(6.4)
记 ,那么有
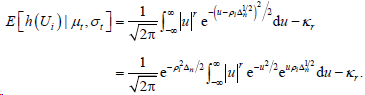 (6.5)
(6.5)
注意到 ,从而有
(6.6)
以及
(6.7)
因此,
(6.8)
利用泰勒展开,我们得到
(6.9)
以及
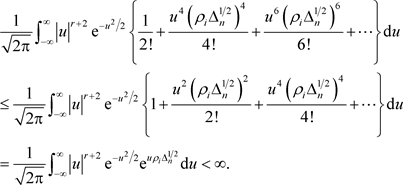 (6.10)
(6.10)
联立(6.8)~(6.10),结论证得。
Lemma 6.2 若条件(A3)和(A4)同时满足,那么对于任意 ,有
(6.11)
根据(A3)里的条件(i),K(u)是有界概率密度函数,还可进一步推得
(6.12)
Proof 由积分中值定理得,存在 ,使得
(6.13)
显然,
(6.14)
而
(6.15)
从而有
(6.16)
(6.17)
结论证得。
Lemma 6.3 假设条件(A1)~(A4)同时满足,那么有
(6.18)
Proof 由积分中值定理得,存在 ,使得
(6.19)
(6.20)
同理,由条件(A3)可知
(6.21)
结论证得。
Lemma 6.4 若条件(A1)~(A4)同时满足,则有
(6.22)
Proof 记
(6.23)
则
(6.24)
根据(1),(2)中对于 和 的定义,我们有
(6.25)
由引理6.1可知
(6.26)
从而结论证得。
