Statistics and Application
Vol.
09
No.
01
(
2020
), Article ID:
34113
,
8
pages
10.12677/SA.2020.91009
Short-Term Load Forecasting Based on Variable Weighted Synthesis of Different Kernel SVM
Dongfen Ma
School of Statistics and Data Science, Xinjiang University of Finance and Economics, Urumqi Xinjiang

Received: Jan. 17th, 2020; accepted: Jan. 31st, 2020; published: Feb. 6th, 2020

ABSTRACT
To improve the accuracy and stability of short-term load forecasting, a method of short-term load forecasting based on different kernel support vector machine (SVM) variable weight synthesis is proposed. In this method, firstly, the load history data is expanded, the feature is selected by correlation analysis, and the historical data is mapped to the input-output relationship view to build the forecasting space. Then, support vector machines of Gaussian kernel, Laplace kernel and Polynomial kernel function are used to study in the forecasting space respectively, and the performance of the model is tested by the 10 fold cross validation. Finally, the variable weight is constructed by using the accuracy and standard deviation of performance test, and the power load forecasting is realized by variable weight synthesis of multiple model. Example analysis shows that compared with methods such as Gaussian kernel support vector machine, partial least squares, decision tree and Bagging, the new method improves accuracy by 0.382%, 3.079%, 3.188% and 2.6%, and stability by 0.383%, 2.452%, 1.781% and 1.43%, respectively.
Keywords:Short-Term Load Forecasting, SVM, Kernel Function, Variable Weight Synthesis of Multiple Models

基于不同核支持向量机变权综合的 短期负荷预测
马冬芬
新疆财经大学统计与数据科学学院,新疆 乌鲁木齐

收稿日期:2020年1月17日;录用日期:2020年1月31日;发布日期:2020年2月6日

摘 要
针对短期负荷预测准确度提升及预测稳定性改进问题,给出了基于不同核支持向量机变权综合的短期负荷预测方法。该方法首先将负荷历史数据进行特征展开,利用相关分析进行特征选择,映射历史数据为输入输出关系视图,构建预测空间。随后,分别采用高斯径向基核函数、拉普拉斯核函数以及多项式核函数的支持向量机在预测空间进行训练学习,使用十折交叉验证进行模型性能测试。最后,利用性能测试的准确率及其标准差构造变权,借助多模型变权综合实现电力负荷预测。实例分析表明,与高斯核支持向量机、偏最小二乘、决策树及Bagging等常用方法相比,新方法将准确度分别提升了0.382%、3.079%、3.188%以及2.6%,将稳定性分别改进了0.383%、2.452%、1.781%以及1.43%。
关键词 :短期负荷预测,支持向量,核函数,多模型变权综合

Copyright © 2020 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
电力负荷预测是指通过研究历史数据变化规律,在满足一定准确度条件下,运用数学方法或建立统计模型的方式对未来几小时、一天到几天的负荷变化做出估计与推断 [1] [2]。准确的电力负荷预测对电网合理规划与电网安全运营具有重要意义 [3]。
电力负荷预测方法可以被归为三类,一类以传统预测方法为主进行预测 [4] [5] [6],例如,Chen J. F.等采用自适应移动平均进行短期负荷预测 [4]。张伏生与汪鸿等使用偏最小二乘方法建立短期负荷预测模型 [5]。万坤等采用ARMA方法构建短期负荷预测模型 [6]。第二类以包含改进型在内的智能预测方法进行预测 [7] - [11],例如,魏立兵与赵峰等采用人群搜索算法优化的支持向量机构建短期负荷预测模型 [7]。Zhang X.等采用布谷鸟优化的支持向量机构建短期负荷预测模型 [8]。梁智等采用PSO优化的深度信念网络进行负荷预测 [9]。吴润泽等采用深度学习进行短期电力负荷预测 [10]。第三类以组合型预测方法为主进行预测 [12] [13] [14] [15],例如,Sudheer G.等构建了组合小波变换、三重指数平滑和加权最近邻的负荷预测模型 [12]。Li Song与Goel Lalit等集成小波变换、极值学习机与偏最小二乘回归进行短期负荷预测 [13]。Wang L.与Lee E. W. M.等结合人工神经网络与集成方法进行负荷预测 [14]。陆继翔等采用混合卷积神经网络与长短期记忆模型进行负荷预测 [15]。
本文沿用组合预测方法,通过变权综合将高斯核函数的支持向量机、多项式核函数的支持向量机以及拉普拉斯核函数的支持向量机进行融合,构建基于多种核支持向量机变权综合的短期负荷预测模型。
2. 支持向量机算法原理
支持向量机是一种常用的统计建模方法,在解决高维度以及非线性问题方面具有优势。设函数表达
式为: ,其中, 为权重向量, 为关于x的映射函数,b为常量。要使 达
到最小,求解最优化问题:
(1)
其中, 表示内积, 为松弛变量,C, 均为参数。使用Lagrange乘数法求解式(1),
(2)
其中, 为Lagrange乘数。求解Lagrange乘数,记 是对应 的解,引入核函数 ,可解得
。
3. 基于不同核支持向量机变权综合的短期负荷预测方法
3.1. 主要思路
基于不同核支持向量机变权综合的短期负荷预测方法主要有以下几个环节:首先,将负荷历史数据进行特征展开,借助相关分析进行特征选取,组建特征集,通过对历史数据进行输入输出关系化展开,构建预测空间。随后,采用高斯径向基核函数(G-K)、拉普拉斯核函数(La-K)、多项式核函数(P-K)支持向量机在预测空间上进行建模,使用交叉验证进行模型性能测试,根据性能测试结果设计不同模型的权重。最后,对三个不同核函数的支持向量机进行变权综合,实现多种核函数支持向量机变权综合的负荷预测。
3.2. 基于相关分析的负荷特征选择
设长度为N的负荷序列 的最大与最小的可能负荷取值为 与 ,取值论域为 。记待预测时刻t对应的负荷为特征 ,t前i个时刻对应的负荷记为特征 ,则对时刻t的负荷进行预测的候选特征集可被记为 。
记待预测时刻点对应的负荷特征
的前m个相邻的向量为:
,其中,
,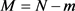 。借助相关度度量
与
之间的相关程度,则
与
之间的相关度可表示为:
。借助相关度度量
与
之间的相关程度,则
与
之间的相关度可表示为:
(3)
的取值为
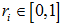 , 越接近于1,
与
之间的相关度越强。设定阈值
,将满足条件的特征所组成的特征集合表示为
。
, 越接近于1,
与
之间的相关度越强。设定阈值
,将满足条件的特征所组成的特征集合表示为
。
3.3. 预测空间构造
以 为输出特征,以特征集 内的特征为输入特征,建立预测空间 。
对给定的历史负荷数据集,在将历史负荷数据进行输入输出关系化展开后,得到关系化数据集为
,其中 ,N为关系化数据记录条数。
3.4. 核函数选择及模型建立
支持向量机中常见的核函数有高斯径向基核函数(Gaussian Basis Kernel, G-K)、拉普拉斯核函数(Laplacian Kernel, La-K)、线性核函数(Linear Kernel, Ln-K)、多项式核函数(Polynomial kernel, P-K)及Bessel核函数等。本文选取常用的高斯径向基核、拉普拉斯核及多项式核用以在关系化数据集上建立不同支持向量机模型。其中,核函数的表达式为:
(4)
(5)
。(6)
3.5. 模型性能测试及变权构造
借助P折交叉验证对不同核函数支持向量机进行性能测试,记第i折的训练数据记录条数为H,测试得到的准确率及其标准差分别为 与 ,
(7)
(8)
依据准确率及其标准差设计每个支持向量机的权重为:
(9)
记不同核函数支持向量机为 ,由 变权综合得到的综合模型可表示为 ,
。
3.6. 基于不同核函数SVM变权综合的负荷预测
基于不同核函数核支持向量机变权综合的短期负荷预测方法的实现可总结为以下几个步骤:
Step 1:确定给定的历史数据集的特征展开参数m,将给定时刻t前m个负荷数据组成电力负荷特征向量 ,。
Step 2:设待预测时刻
,,确定负荷预测备选特征集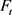 ,采用相关度分析进行特征选取,组建特征集
,进而对历史数据集进行关系化展开,构建待预测时刻的预测空间
。
,采用相关度分析进行特征选取,组建特征集
,进而对历史数据集进行关系化展开,构建待预测时刻的预测空间
。
Step 3:选用高斯径向基核函数、拉普拉斯核函数及多项式核函数的支持向量机在预测空间上建立预测模型,借助P折交叉验证进行模型测试。
Step 4:依据性能测试结果的准确度 及其标准差 构造变权,通过变权综合不同核函数的SVM实现 的负荷预测。令 ,当 ,则预测结束;否则,转Step 2。
4. 算例分析
选用东肯塔基州电力合作社的2018年采样间隔为1小时的电力负荷数据进行实例分析,R语言作为算例分析的实现工具。取1月1日~4月23日的电力负荷时间序列作为训练数据,取值论域
,单位:MW。分别采用高斯核函数、多项式核函数以及拉普拉斯核函数的支持向量机进行建模,预测4月24日~30日(记为
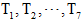 )的电力负荷值。以预测T1第一时刻
的电力负荷过程为例,其余时刻点负荷以相同步骤滚动预测获得。
)的电力负荷值。以预测T1第一时刻
的电力负荷过程为例,其余时刻点负荷以相同步骤滚动预测获得。
计算 的负荷特征 与历史负荷特征 之间的加权相关度,结果如图1所示。

Figure 1. Correlation between load feature to be forecast and historical load features
图1. 待预测负荷特征与历史负荷特征的相关度
上图所示,待预测负荷特征与历史负荷特征之间的相似度呈衰减趋势。确定阈值
,则选出的特征组成的相关特征集
。以
为输出,特征集中的特征为输入,构建关于待预测时刻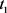 的预测相空间
。通过将历史数据输入输出关系化,得到关系化数据集。
的预测相空间
。通过将历史数据输入输出关系化,得到关系化数据集。
分别采用不同核函数的支持向量机在训练集上建立模模型,并借助十折交叉验证对支持向量机进行测试,依据测试得到的准确度及其标准差计算权重,综合不同核函数支持向量机的预测结果,得到预测值1119.452 MW。
更新训练集与测试集以滚动预测其它时刻的电力负荷。采用预测模型的相平均绝对百分比误差(Mean Absolute Percentage Error, MAPE)以及相对误差的标准差(SRE)作为评价指标进行评价,其中
(10)
(11)
对变权综合模型(C-SVM)与常用的高斯核函数SVM (G-SVM)、偏最小二乘(PLS)、决策树(DT)以及Bagging等预测方法进行对比分析。T1的预测结果如图2所示。

Figure 2. Comparison of power load forecasting values
图2. 电力负荷预测值对比
如图2所示,对比几种方法预测值的曲线与真实值曲线的差异,C-SVM预测值的曲线与真实真实值曲线最为贴近,其次是G-SVM,但在谷处的预测不及C-SVM,偏离了真实值。DT与Bagging预测值曲线围绕较真实值曲线上下波动,但与真实值曲线偏离最为明显。
对比以上模型预测24~30日负荷得到的MAPE值,如表1所示。
Table 1. MAPE of forecast models
表1. 模型预测所得的MAPE
注:表中数据均为百分数。
如表1所示,C-SVM所得MAPE普遍小于其它方法的MAPE,MAPE的均值为1.303%,最大值为2.171%。对比G-SVM、PLS、DT以及Bagging,C-SVM将预测准确度分别改进了0.382%、3.079%、3.188%、2.6%;并将最大MAPE值分别改进了0.334%、3.431%、3.385%以及2.47%。
对比以上模型预测24~30日负荷所得的MRE值,结果如表2所示。
Table 2. SRE of forecast models
表2. 模型预测所得的SRE
注:表中数据均为百分数。
如表2所示,C-SVM的SRE值大部分小于1%,可知C-SVM在预测过程波动幅度不大,预测相对稳定。与G-SVM、PLS、DT以及Bagging的SRE均值相比,C-SVM将预测稳定性分别改进了0.383%、2.452%、1.781%以及1.43%。
5. 总结
本文针对短期负荷预测准确度提升及预测稳定性改进问题,建立了基于不同核函数支持向量机变权综合的预测模型。利用相关分析实现了特征选取,采用交叉验证进行了模型性能测试,结合测试结果构造了变权,通过变权融合实现了基于综合模型的负荷预测。东肯塔基州电力合作社的实例分析结果证明,与高斯核函数的SVM、偏最小二乘、决策树以及Bagging等单一模型相比,新方法将体现准确度的MAPE均值分别改进了0.382%、3.079%、3.188%、2.6%;将最大MAPE值分别改进了1.52%、4.62%、41.34%、3.3%以及4.43%;将最大相对误差的均值改进了0.334%、3.431%、3.385%以及2.47%。将体现稳定性的SRE均值分别改进了0.383%、2.452%、1.781%以及1.43%。可见。多模型变权综合是一种提升负荷预测准确度与稳定性的有效方式,今后,可对变权设计及综合方式进行深入研究。
基金项目
新疆财经大学研究生科研创新项目(XJUFE2018K043)。
文章引用
马冬芬. 基于不同核支持向量机变权综合的短期负荷预测
Short-Term Load Forecasting Based on Variable Weighted Synthesis of Different Kernel SVM[J]. 统计学与应用, 2020, 09(01): 73-80. https://doi.org/10.12677/SA.2020.91009
参考文献
- 1. 康重庆, 夏清, 刘梅. 电力系统负荷预测[M]. 北京: 中国电力出版社, 2017, 1-17.
- 2. Khan, A.R., Mahmood, A., Safdar, A., et al. (2016) Load Forecasting, Dynamic Pricing and DSM in Smart Grid: A Review. Renewable & Sustainable Energy Reviews, 54, 1311-1322. https://doi.org/10.1016/j.rser.2015.10.117
- 3. 顾熹, 廖志伟. 基于相空间重构和高斯过程回归的短期负荷预测[J]. 电力系统保护与控制, 2017, 45(5): 73-79.
- 4. Chen, J.F., Wang, W.M. and Huang, C.M. (1995) Analysis of an Adaptive Time-Series Autoregressive Moving-Average (ARMA) Model for Short-Term Load Forecasting. Electric Power Systems Research, 34, 187-196. https://doi.org/10.1016/0378-7796(95)00977-1
- 5. 张伏生, 汪鸿, 韩悌, 等. 基于偏最小二乘回归分析的短期负荷预测[J]. 电网技术, 2003, 27(3): 36-40.
- 6. 万坤, 柳瑞禹. 区间时间序列向量自回归模型在短期电力负荷预测中的应用[J]. 电网技术, 2012, 36(11): 77-81.
- 7. 魏立兵, 赵峰, 王思华. 基于人群搜索算法优化参数的支持向量机短期电力负荷预测[J]. 电测与仪表, 2015, 53(8): 45-49.
- 8. Zhang, X.B., Wang, J.Z. and Zhang, K.Q. (2017) Short-Term Electric Load Forecasting Based on Singular Spectrum Analysis and Support Vector Machine Optimized by Cuckoo Search Algorithm. Electric Power Systems Research, 146, 270-285. https://doi.org/10.1016/j.epsr.2017.01.035
- 9. 梁智, 孙国强, 等. 基于VMD与PSO优化深度信念网络的短期负荷预测[J]. 电网技术, 2018, 42(2): 598-606.
- 10. 吴润泽, 包正睿, 宋雪莹, 等. 基于深度学习的电网短期负荷预测方法研究[J]. 现代电力, 2018, 35(2): 43-48.
- 11. 杨芳君, 王耀力, 王力波, 等. 基于改进CS算法优化Elman-IOC神经网络的短期负荷预测[J]. 电测与仪表, 2019, 56(9): 39-44.
- 12. Sudheer, G. and Suseelatha, A. (2015) Short Term Load Forecasting Using Wavelet Transform Combined with Holt-Winters and Weighted Nearest Neighbor Models. International Journal of Electrical Power & Energy Systems, 64, 340-346. https://doi.org/10.1016/j.ijepes.2014.07.043
- 13. Li, S., Goel, L., and Wang, P. (2016) An Ensemble Approach for Short-Term Load Forecasting by Extreme Learning Machine. Applied Energy, 170, 22-29. https://doi.org/10.1016/j.apenergy.2016.02.114
- 14. Wang, L., Lee, E.W.M. and Yuen, R.K.K. (2019) Novel Dynamic Forecasting Model for Building Cooling Loads Combining an Artificial Neural Network and an Ensemble Approach. Applied Energy, 228, 1740-1753. https://doi.org/10.1016/j.apenergy.2018.07.085
- 15. 陆继翔, 张琪培, 等. 基于CNN-LSTM混合神经网络模型的短期负荷预测方法[J]. 电力系统自动化, 2019, 43(8): 191-197.
