ABSTRACT

Previously, there were many studies about the problem of representation of natural numbers. But it’s comparatively rare to study the problem based on Fibonacci sequence and its extension. This thesis mainly discussed the feasibility and diversity of this kind of representation. Utilizing enumerating polynomials and binomial codes, we focused on minimal and maximal representations of natural numbers. In addition to Fibonacci sequence, we also studied the situation of Lucas sequence and offered some hypotheses in the case of n-step Fibonacci sequence.

Keywords:Representation of Natural Numbers, Fibonacci Sequence, Enumerating Polynomial, Binomial Code

Fibonacci数列及其推广形式的正整数表示

郭婷婷¹，晁福刚¹，任 韩^1,2*

¹华东师范大学数学系，上海

²上海市核心数学与实践重点实验室，上海

收稿日期：2016年4月24日；录用日期：2016年5月10日；发布日期：2016年5月13日

摘 要

正整数表示问题前人多有研究，而基于Fibonacci数列及其推广形式的分析并不多见。本文的主要工作是探讨了该类整数表示的可行性，发现了表示的多样性，从而从最少表示及最多表示的角度来展开分析，分别引入了它们的计数多项式以及0与1的编码形式。起初是只针对Fibonacci数列，之后研究Lucas数列的情况，再接着对一类推广：n代的Fibonacci数列做了猜测。

关键词 :正整数表示，Fibonacci数列，计数多项式，二项编码

1. 引言

中世纪意大利数学家Leonardo Fibonacci提出了如下的“兔子问题”：在一年初把一对兔子(雌雄各一)放入围墙内，从第二个月起，雌兔每月生一对兔子(雌雄各一)，而雌小兔长满足两个月后开始生小兔子，也是每月生一对兔子(雌雄各一)，问到了年底墙内共有多少对兔子。这就是著名的Fibonacci数列。

Fibonacci数列与许多数学概念联系密切，并具有许多漂亮的性质。人们在许多表面上看似没有任何联系的问题中都发现了它们，使得这一数列成为很基本的一个数学对象。例如：上n阶楼梯，每次只能上1阶或2阶，的不同方法数。就是与Fibonacci数列有相同的初始值和递推关系的数列。一个更有趣的事实是这个正整数的序列，它的通项竟然可以用无理数来表示。

美国数学会专门出版了一份以《Fibonacci Quarterly》为名的数学杂志，来刊载这方面的研究成果。本文所研究的正整数表示问题的很多参考文献也是来源于此。

2. 正整数表示的存在性和最多与最少的表示问题

为了证明存在性，先引入一个概念：对于一个非负递增数列，若所有正整数都能写成数列中的某些元素的和，且每个元素最多用一次，则该数列是完全数列 [1] 。

数列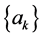是完全数列的一个充要条件是，其中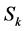为数列的和函数。因而可以推知当等号成立时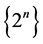，是满足条件的最小数列。这也是每个正整数都有二进制表示的理由。

数列是完全数列的一个充分条件是，易验证Fibonacci数列满足该不等式，从而Fibonacci数列是完全数列，任何正整数都可以基于Fibonacci数列表示。

如果我们将任意正整数写成不同的Fibonacci数的和，且涉及的数字最多用一次，例如：10 = 8 + 2 = 2 + 3 + 5 = 1 + 1 + 3 + 5，可以发现会有很多种表示方法，那不禁要问最多与最少的表示分别是什么 [2] 。

若是最少表示的话，相邻的Fibonacci数是不能同时出现的。试想一下，若与同时出现在表示中，则为了用最少的数字来表示某个整数，它们可以被所取代。

为了更好地分析该问题，我们需要引入一个0与1的纸盒模型。将命题“关于中不相邻的子集个数是”，做如下推广。考虑n个盒子，每个盒子里要么装0要么装1，连续的两个盒子里不能都装1，那么这样的装法数为种。如果再排除全部装0的情况，则只有种装法。换句话说，由n个不相邻的且不同的Fibonacci数能表示的最大数是。

回到提出的问题，由于要使用不同的Fibonacci数，则我们必须舍去，n个盒子分别按照顺序表示，取1则表示使用这个Fibonacci数，取0则表示不使用。

基于最少表示的限定条件：相邻的Fibonacci数不能出现，那么我们也能很容易得出恒等式即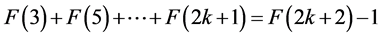(有2k个盒子)； (有个盒子)。

对于每一个在中的整数，我们定义一个最少表示的计数多项式，多项式中的每一项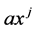表示有a个整数需j用个Fibonacci数表示。例如：对于中的整数的最少表示分别为8 = 8，9 = 8 + 1，10 = 8 + 2，11 = 8 + 3，12 = 8 + 3 + 1，由此可得该段区间内的最少计数多项式为。从该例子中还能发现一个特点，即：对于每一个中的整数Fibonacci的最少表示一定会含有。如果不含有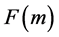，那么此区间内的最少表示是不能实现的，否则得取相邻的Fibonacci数了，而这已经不是最少表示了。

表1罗列了前9个最少计数多项式。

接下来我们可以简单地推导一下该最少计数多项式的递推公式。

显然对于的最少计数多项式可以拆成与的两个最少计数多项式的和。

如果我们在每一个的整数最少表示中加入，则我们可以得到，即的最少计数多项式为。

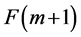对于所有整数的最少表示中都会含有，如果我们将用代替，即可得到的最少计数多项式，也是。

从而我们能够得到的最少计数多项式，即递推公式：

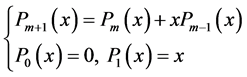
另外不难注意到，对于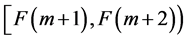的最少计数多项式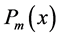的所有系数的和为，该值也表示该区间所有整数的个数即。所以在上述递推关系中若令，则可得到Fibonacci数列的递推关系。

此外，如果我们再结合之前提到的盒子问题，用0和1编码的形式来展示上述过程会更简单明了地看出递推关系。需要注意的是最少表示中必须满足任意两个1不能相邻的条件。表2展示了[13,21)至[21,34)的整数Fibonacci最少表示的变化过程。

3. Fibonacci最少表示的唯一性与其最多表示

由Zeckendorf定理 [3] 可知，对于每个正整数n有唯一的Fibonacci最少表示，即必须由不相邻的数组成。可以用反证法证明如下，若n有两个不同的表示，即

其中，。

令k是满足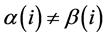的最大指标，则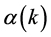与中有一个是0有一个是1，不妨设。因此，且由该等式右边能导出，而左边，其中，与前一导出

表1. Fibonacci的最少计数多项式

表2. Fibonacci最少表示的递推关系

矛盾，得证。

反过来，如果我们为了得到最多的表示，则尽可能要用相邻的Fibonacci数。再回到之前提到的装满0和1的盒子，这次我们希望不要出现相邻的0，即n个1中最多插入一个0。在任何一串连续的1中，0可以出现在最左边的1的旁边也可以出现在最右边的1的旁边。

现在考虑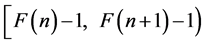中整数的最多计数多项式。同样的多项式中的每一项表示有a个整数需用j个Fibonacci数表示。例如：对于中的整数的最多表示分别为7 = 5 + 2, 8 = 5 + 2 + 1, 9 = 5 + 3 + 1, 10 = 5 + 3 + 2, 11 = 5 + 3 + 2 + 1，由此可得该段区间内的最多计数多项式为。

从该例子中还能发现一个特点，即：对于每一个中的整数Fibonacci的最多表示一定会含有。

表3罗列了前8个最多计数多项式。

参照之前的做法，同样可以得到最多计数多项式的递推关系：

同样地，我们也可以用编码的形式来直观地看出这个递推关系。表4展示了[7,20)至[20,33)的整数Fibonacci最多表示的变化过程。

4. Fibonacci的表示数

我们定义表示n用Fibonacci数表示的所有可能数目，则可以通过贪婪算法得出前60个正整数的情况表5。

然而随着n不断变大，计算机的存储空间有限将不能继续运算，为此有些数学家就推导了一些关于的递推关系，研究了该表示数的一些性质 [4] 。

5. Lucas的表示

如果我们将Fibonacci数换成Lucas数，即：探讨基于此数的正整数表示 [5] 。同样的，我们对中的每个整数定义一个最少计数多项式多项式中的每一项表示有d个整数需用j个Lucas数表示。例如：对于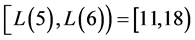中的整数的最少表示分别为，，，，，，，由此可得该段区间内的最少计数多项式为，从该例子中也能发现一个特点，即：对于每一个中的整数Lucas的最少表示一定会含有。

表3. Fibonacci的最多计数多项式

表4. Fibonacci最多表示的递推关系

由于Fibonacci和Lucas只是初项不同，两者的递推关系是一样的，从而我们可以推测两者的计数多项式的递推关系应该也是一样的。可以看表6用编码展示的Lucas最少计数多项式的递推关系变化过程。 至于Lucas的最多计数多项式的内容和之前的Fibonacci类似，在此就不再赘述。

另外Lucas的最少表示是否与Fibonacci一样也是唯一的呢？答案是否定的。例如：，若仍想保证表示的唯一性，则当同时出现时，只能选择其一。

6. n代Fibonacci数列的表示

最后我们考虑一下n代的Fibonacci数列是否有上述提及的类似性质 [6] 。

我们称数列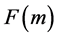为n代的Fibonacci数列，当且仅当

表5. n用Fibonacci数表示的所有可能数目

表6. Lucas最少表示的递推关系

该数列的特征方程是，将此等式两边同乘以，即化成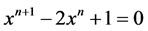，之后再同时除以，可得。所以该数列的特征根也是方程的根。由于该方程的极限是，从而可知n代Fibonacci数列也会收敛到数列。

从而我们可以推断n代Fibonacci数列也会是完全数列。所以任何正整数也会有n代Fibonacci数列的表示。

同样的，我们也能够考虑n代Fibonacci数列的计数多项式的递推。如果从编码的角度，需要注意的一个规则是：n代的最少编码是至多个1连在一起，n代的最多编码是至多个0连在一起，这是由数列的递推关系决定的。

基金项目

本项研究工作得到了上海市科学技术委员会的资助，资助课题编号为13dz2260400；同时受到中国国家自然科学基金项目资助(项目批准号：11171114)，在此表示感谢。

文章引用

郭婷婷,晁福刚,任韩. Fibonacci数列及其推广形式的正整数表示
Representation of Natural Numbers Using Generalized Fibonacci Sequence[J]. 应用数学进展, 2016, 05(02): 225-231. http://dx.doi.org/10.12677/AAM.2016.52029

参考文献 (References)