Advances in Applied Mathematics
Vol.06 No.04(2017), Article ID:21290,6
pages
10.12677/AAM.2017.64057
Application of Seemingly Unrelated Model in the Study of Food Production
Bo Wang*, He Zhang
School of Math and Physics, China University of Geosciences, Wuhan Hubei

Received: Jun. 18th, 2017; accepted: Jul. 4th, 2017; published: Jul. 7th, 2017

ABSTRACT
The traditional linear model is usually used in the study of grain yield ,in which the error terms are assumed independent of each other, and the parameters are estimated by the least squares method. In order to improve the estimation accuracy, seemingly unrelated model is introduced. Least squares model and seemingly unrelated model were built with the data that the yield, planting area and irrigation area of rice, wheat and corn between 1990 and 2009. The result showed that parameter variance of seemingly unrelated model is smaller than the least square model. The output of the three kinds of grain between 2010 and 2015 was predicted by the two models, and the average prediction error of seemingly unrelated model was smaller. It shows that there is some correlation between the yields of the three grain crops, and the seemingly unrelated model is better than the traditional least square model.
Keywords:Seemingly Unrelated, Least Square Method, Grain Yield, Parameter Estimation
似乎不相关模型在粮食产量研究中的应用
王博*,张贺
中国地质大学(武汉)数学与物理学院,湖北 武汉

收稿日期:2017年6月18日;录用日期:2017年7月4日;发布日期:2017年7月7日

摘 要
对粮食产量的研究一般采用传统的线性模型,假设方程误差项相互独立,采用最小二乘法进行参数估计。为提高模型的估计精度,引入似乎不相关模型,以1990~2009年稻谷、小麦、玉米的产量、种植面积和有效灌溉面积数据分别建立最小二乘模型和似乎不相关模型。结果显示似乎不相关模型的参数方差一致小于最小二乘模型,用两种模型分别对2010~2015年的三种粮食产量进行预测,似乎不相关模型预测的平均误差更小。说明三种粮食的产量之间存在一定的相关性,似乎不相关模型较传统的最小二乘模型效果更好。
关键词 :似乎不相关,最小二乘法,粮食产量,参数估计

Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
似乎不相关模型最早由Zellner于1962年提出 [1] ,它是联立几个回归方程的特殊线性模型,允许模型方程的自变量及变量个数不同,使得模型建立更加方便,大大增加了其应用范围。同时,似乎不相关模型考虑了各方程误差项间的相关性,认为模型不同观测之间互不相关,而同一观测之间是相关的,且有相同的方差矩阵,这种特殊的误差结构使得其参数估计方法和效果不同于普通的最小二乘模型,也是“似乎不相关”名称的由来。
2. 模型理论
2.1. 最小二乘模型理论
设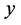 为因变量,
为因变量, 为自变量,它们存在如下的线性关系:
为自变量,它们存在如下的线性关系:
 (1)
(1)
对(1)式中的 和
和 进行
进行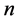 次独立观测,得到
次独立观测,得到 组样本数据
组样本数据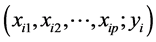 ,
, ,记
,记
 ,
,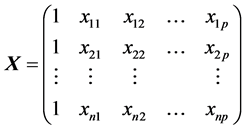 ,
, ,
,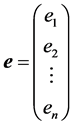
假定不同误差项之间相互独立,且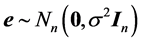 ,则有
,则有
 (2)
(2)
(2)式是常见的多元线性模型,也叫线性回归模型 [2] 。对参数 的估计,常采用最小二乘法,当矩阵
的估计,常采用最小二乘法,当矩阵 列满秩时,
列满秩时, 的最小二乘估计量为
的最小二乘估计量为
 (3)
(3)
此估计量为最优线性无偏估计量。
2.2. 最小二乘模型理论
设 为因变量,
为因变量, 为对应的自变量,它们满足如下的线性关系:
为对应的自变量,它们满足如下的线性关系:
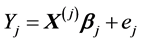 ,
, (4)
(4)
其中,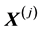 为
为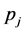 维行向量,
维行向量,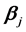 为
为 维列向量,
维列向量, 为第
为第 个方程的误差项。需要注意的是每个方程中的自变量
个方程的误差项。需要注意的是每个方程中的自变量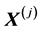 及其个数
及其个数 不一定相同. 在得到样本观测值
不一定相同. 在得到样本观测值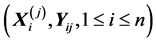 后,则有下面的关系:
后,则有下面的关系:
 ,
, (5)
(5)
假设误差项均值为0,不同观测的误差项互不相关,且有相同的方差矩阵,即
 ,
, ,
,
其中 。记
。记
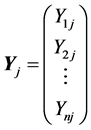 ,
,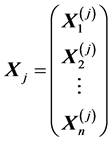 ,
,
则有
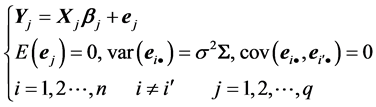 (6)
(6)
模型(6)称为似乎不相关模型 [3] 。再记
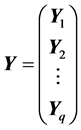 ,
, ,
, ,
,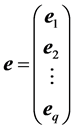
则可将(6)写成广义一元线性模型的形式:
 (7)
(7)
其中,“ ”表示矩阵的Kronecker乘积运算符 [4] 。根据广义一元线性模型的理论,当矩阵
”表示矩阵的Kronecker乘积运算符 [4] 。根据广义一元线性模型的理论,当矩阵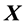 列满秩时,似乎不相关模型(6)中参数
列满秩时,似乎不相关模型(6)中参数 的估计为:
的估计为:
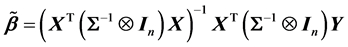 (8)
(8)
当方差矩阵 未知时,常采用二步回归法。先计算参数
未知时,常采用二步回归法。先计算参数 的最小二乘估计量:
的最小二乘估计量: ,然后估计矩阵
,然后估计矩阵 的元素:
的元素:
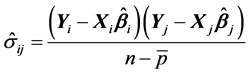 (9)
(9)
其中 ,记
,记 ,可得
,可得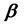 的估计量为:
的估计量为:
 (10)
(10)
称 为似乎不相关估计量,它是
为似乎不相关估计量,它是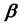 的无偏估计量,其方差为
的无偏估计量,其方差为
 (11)
(11)
3. 实例分析
3.1. 粮食产量的线性模型
粮食产量是关系国家发展的一个重要问题,各个邻域的专家和学者都十分重视对粮食产量问题的研究 [5] 。目前,关于粮食产量常用的模型有线性回归、时间序列、灰色预测、神经网络等 [6] 。线性模型是最简单实用的一种模型,但由于粮食产量影响因素较多,具有很大的随机性和突变性,往往效果不好。似乎不相关模型是一种改进的线性模型,将其运用到粮食产量问题中,具有一定的意义。
影响粮食产量的因素主要有粮食种植面积、化肥施用量、受灾面积、农业机械总动力、灌溉面积、人口密度等 [7] 。
假设粮食产量与其影响因素满足如下的线性关系:
 (12)
(12)
其中,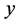 为粮食产量,
为粮食产量, 为种植面积,
为种植面积, 为灌溉面积。以1990~2009共20年的数据(数据来源于中国统计年鉴),分别建立三种农作物的线性回归模型:
为灌溉面积。以1990~2009共20年的数据(数据来源于中国统计年鉴),分别建立三种农作物的线性回归模型:
 (13)
(13)
其中,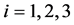 分别代表稻谷、小麦、玉米三种农作物。考虑到三个方程误差项间存在相关性,将其联立得到似乎不相关模型
分别代表稻谷、小麦、玉米三种农作物。考虑到三个方程误差项间存在相关性,将其联立得到似乎不相关模型
 (14)
(14)
这里 ,
, ,
, ,
, 。
。
3.2. 结果对比与预测
分别计算得到三种农作物的回归方程:
稻谷:
小麦: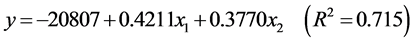
玉米:
模型的拟合效果较好。
似乎不相关模型中,参数估计结果为:



由于两种模型中参数 的估计均为无偏估计,有必要比较其方差。 方差矩阵中对角线上的元素代表参数
的估计均为无偏估计,有必要比较其方差。 方差矩阵中对角线上的元素代表参数 各分量的方差,表1列出两种模型三个方程的参数
各分量的方差,表1列出两种模型三个方程的参数 各分量的方差。
各分量的方差。
对比表1中两种模型的方差结果,可以发现似乎不相关模型中参数 各分量的方差都略小于最小二乘模型,说明似乎不相关模型的参数估计更有效 [8] 。
各分量的方差都略小于最小二乘模型,说明似乎不相关模型的参数估计更有效 [8] 。
分别用两种模型对2010~2015年的粮食产量进行预测,结果如表2所示。
结果显示,最小二乘模型中,三种农作物预测产量相对真实值的平均误差分别为4.29%、7.38%、3.28%,而似乎不相关模型的平均相对误差分别为4.08%、5.95%、3.08%,误差分别减小了4.90%、19.38%、6.10%。
4. 总结
本文以粮食产量、种植面积及灌溉面积为变量,分别对稻谷、小麦、玉米建立独立的最小二乘模型和三个方程联立的似乎不相关模型,结果表明似乎不相关模型的参数方差小于最小二乘模型,估计更有效。用两种模型对后续的粮食产量进行预测,似乎不相关模型的平均相对误差整体上小于最小二乘模型,
Table 1. Variance of the parameters of the two models
表1. 两种模型参数 各分量方差
各分量方差
Table 2. Prediction results of the two models (Unit: Million tons)
表2. 两种模型预测结果(单位:万吨)
说明前者的预测精度更高。总体来说,由于似乎不相关模型考虑了方程误差项间的相关性,参数估计的效果比最小二乘模型更好,模型优于传统的最小二乘模型。
文章引用
王博,张贺. 似乎不相关模型在粮食产量研究中的应用
Application of Seemingly Unrelated Model in the Study of Food Production[J]. 应用数学进展, 2017, 06(04): 481-486. http://dx.doi.org/10.12677/AAM.2017.64057
参考文献 (References)
- 1. Zellner, A. (1962) An Efficient Method of Estimating Seemingly Unrelated Regressions and Tests for Aggregation Bias. Journal of the American Statistical Association, 57, 348-368.
- 2. 向东进, 李宏伟, 刘小雅. 实用多元统计分析[M]. 武汉: 中国地质大学出版社, 2005.
- 3. 唐守正. 生物数学模型的统计学基础[M]. 北京: 科学出版社, 2002.
- 4. 许君一, 孙伟, 齐东旭. 矩阵Kronecker乘积及其应用[J]. 计算机辅助设计与图形学学报, 2003, 15(4): 377-388.
- 5. 陈秧分, 李先德. 中国粮食产量变化的时空格局与影响因素[J]. 农业工程学报, 2013, 29(20): 1-10.
- 6. 林芳. 灰色神经网络在粮食产量预测中的应用[J]. 计算机仿真, 2012(4): 225-228.
- 7. 顾乐民. 基于最小一乘准则的中国粮食产量与影响因素的相关性分析[J]. 农业工程学报, 2013(11): 1-10.
- 8. 罗文强, 冀雅楠, 王淳越, 宋子健. 多监测点滑坡变形预测的似乎不相关模型研究[J]. 岩石力学与工程学报, 2016(S1): 3051-3056.
NOTES
*通讯作者。
