Advances in Applied Mathematics
Vol.06 No.08(2017), Article ID:22809,7
pages
10.12677/AAM.2017.68118
A Three-Way Spectral Clustering Algorithm Based on Perturbation Analysis
Xiaolei Wang, Pingxin Wang*
School of Science, Jiangsu University of Science and Technology, Zhenjiang Jiangsu
*通讯作者。

Received: Nov. 8th, 2017; accepted: Nov. 21st, 2017; published: Nov. 27th, 2017

ABSTRACT
We structure a three-way Clustering Algorithm Based on NJW Algorithm. The main idea is that each object, making weighted arithmetic, repeats clustering arithmetic to obtain the weighted results, which benefits from the stability of NJW Algorithm. According to the perturbation for all objects, we can classify the object into core or fringe regions. The compact degree of core and fringe regions can be described by the modified S_Dbw(c) index. Testing the algorithm on the artificial and UCI data sets, the results meet expectation.
Keywords:Three-Way Clustering, Disturbance Degree, NJW Algorithm
一种基于扰动分析的三支谱聚类算法
王晓磊,王平心*
江苏科技大学理学院,江苏 镇江

收稿日期:2017年11月8日;录用日期:2017年11月21日;发布日期:2017年11月27日

摘 要
本文在多路谱聚类算法(NJW算法)的基础上进行三支聚类算法构造。主要思想是针对每个对象进行加权运算,利用多路谱聚类算法的稳定性,重复进行聚类运算从而获得加权结果。根据其加权后对全体对象的扰动影响,将其划入核心域或边界域。对S_Dbw(c)指标进行改造使其可以表示核心域与边界域的离散程度。最后分别在人工与UCI数据集上对算法进行测试,有较好效果。
关键词 :三支聚类,扰动影响,谱聚类

Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
聚类 [1] [2] [3] 可以看作一种分类,是将具有一定相似度的对象按照其自身的特性进行分类,是当代分类学与多元分析的结合,并已用于多个领域 [4] 。由于聚类所生成的簇是一组数据对象的集合,这些对象与同一个簇中的对象彼此相似,与其他簇中的对象相异。在聚类的研究和应用中存在两个主要问题 [5] 。首先,如何有效的划分一个数据集。其次,如何确定划分出的类簇个数。使用不同的算法思想对同一个数据集进行操作往往会产生不同的聚类结果。产生分歧的原因往往是一些元素特征并不明显或过于明显,使得在分类过程中既可以被分入这个类也可以被分入那个类。因此会降低聚类的效果。
聚类结果的效果如何,取决于数据集中各个元素能否依照算法准确地被划分入相应类簇。无法被准确分类的元素除特征明显,与其余点明显相异的噪点(孤立点),还有介于两类簇之间,既可以被划入此类簇也可以被划入彼类簇的边界点。因此引入三支聚类的概念,依照核心域,边界域,琐碎域对数据集进行划分,解决了由于特征不清导致分类不准的问题。
2. 相关工作与概念
目前,大多二支聚类结果都是一种硬划分,即对某一个元素都有唯一确定的类簇与之匹配。而在某些数据集中,由于数据本身特征存在模糊与相异度较低的情况,无法对其进行准确的划分,此时被强制分配的元素会大大降低二支聚类结果的精度,破坏其结构。例如图1所示,位于中间的元素在两类簇的边界处出现交叉,其依照算法被划分为两类,但是从观察中可得这些元素并未明显差异。
以下介绍三支聚类的有关概念:
设给定一个数据集 ,依照二支聚类的定义,由一个集合代表一个类簇,即寻找一组集合 满足 ,且满足 , ,其中k为聚类的个数。
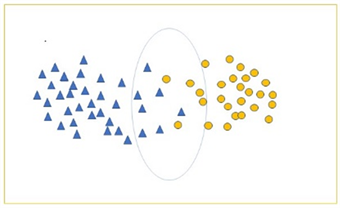
Figure 1. A schematic diagram of data set
图1. 数据集示意图
在三支聚类中,使用三个互不相交的集合表示一个类,即 , 与 ,分别称为类的核心域,边界域和琐碎域,其中
(1)
核心域中的元素确定属于这个类,边界域中的元素可能属于也可能不属于这个类,而琐碎域中的元素则肯定不属于这个类。由关系式(1),我们可以通过 和 来表示一个类。反过来,如果给定一组集合 , , 满足
(2)
(3)
我们称其为数据集U三支聚类。其中(2)要求正域非空,即每个类中至少有一个对象,而(3)保证每个对象至少被分到一个类中。和传统的硬聚类的结果 不同,三支聚类的结果应为如下形式,
显然在三支聚类中如果有 , ,就变成了 传统二支决策的聚类形式。因此,三支决策聚类形式是传统二支聚类方法的推广,使用边界域去解决针对目前知识体系下难以聚类的对象,或是特征不明显难以准确归类的元素,即为三支聚类的主要思想。
3. 基于扰动的三支聚类算法
本算法的主要思想是对每个对象进行加权处理,之后依照前后对比进行分类。首先使用NJW算法对数据集进行一次划分,之后在此次划分基础上对选定对象加权重新聚类,比较两次聚类的扰动情况。从图1中可以看出属于边界域的点往往会呈现一种边缘性,正是因为这种边缘性使得划分结果的不准确。边缘性反映在数据上即为元素距类簇中心的距离,但是单独判断显然不是一个可行方法。首先。作为一种无监督学习,在分析之前不知道判断距离的标准。其次,单纯的判断距离无法识别出所判断点所处区域的数据稠密情况,疏密情况对于域的划分有着显著的影响,最后,距离判断误差极大,一次性会将某一范围外的所有点归为边界域,失去参考价值。所以本文采用扰动的方法,设立标准扰动量,计算每个点加权后对全局的扰动,与标准扰动量进行比较判断所属域。
参数m为对某点添加新点的个数,通常为聚类总对象数量的特定倍数。通常这个倍数不易过大,一旦过大,新的类簇中心必然出现在选定点上,此时就转换为单纯的比较距离。失去了扰动算法的本质意义。
标准扰动距离并非一成不变,而是针对不同的数据集特意选定。并且标准扰动距离与参数m呈正相关(当添加的点愈多,偏移愈大)。两者需要考量数据集的形状,类型,才能较好的选定。这里给出一种通常的选定方式,通常把数据集分位数进行加权处理,以此作为标准扰动距离。
算法1: 基于全局扰动的三支谱聚类算法
Step1 通过NJW算法对数据集U进行一次聚类操作,得到 ;
Step 2 在数据集中任找一个尚未被判断的点q,在原本数据集中添加m个数据q得到新数据集 ,对 应用NJW算法重新聚类,得到 。
Step3在 中找到q所对应的聚类 ,比较两聚类中心的欧氏距离,当其距离差值大于标准扰动聚类w时,将q划分至边界域,反之,将q划分至核心域。
Step4 若q以外所有点都已被判断则转入Step5,否则转入Step2。
Step5 输出核心域与边界域。
由于算法本身的不足,造成此算法的时间复杂度极大。这是由于在聚类过程中对于每个点都要进行一次聚类操作,并且每此参与聚类的数据量还大于原数据集。为了解决上述问题,以下考虑一种基于局部的聚类算法。仅在初始时进行一次聚类运算,之后在判断聚类中心时仅仅在一个类簇内进行考虑而非对全部数据进行操作。以此大大简化了运算量,当然精度不可避免的造成一定损失。但是经实验检测,此算法依然有较好的实验效果。
算法2:基于局部扰动的三支谱聚类算法
Step1 通过NJW算法对数据集U进行一次聚类操作,得到 ;
Step 2 在数据集中任找一个尚未被判断的点q, ,在原本数据集U中添加m个数据得到新数据集 ,找到q原本所在类簇 。记 。
Step3计算 的聚类中心,将其与原本C的中心进行比较,若欧式距离差大于标准扰动距离与扰动系数的乘积则将其划分至边界域,反之,将其划分至核心域。
Step4 若q以外所有点都已被判断则转入Step5,否则转入Step2
Step5 输出核心域与边界域。
基于局部的算法中,将原本需要重新聚类获得的聚类中心转变为直接在原本类簇中增加相应的点进行求中心处理。由于不需要考虑全局,可以取较小值,将添加的类簇数据量倍数记为扰动系数。这是因为单个聚类本身具有极好的扰动特性(完全的物理特性)。此时标准扰动距离与扰动系数的乘积在实验中有良好的表现。
4. 实验结果
4.1. 人工数据集
本节采用一组人工数据集U,U为从均值为 ,协方差为 的正态分布中抽取 的矩阵r(n为样本数,d为样本维数,本实验d为2)。
其中, ,R中的每一行以中对应的行为均值的正态分布中抽取的一个样本。同时
, 表示在0~1中取随机数。
,对于 有 。
此为基于局部的NJW算法的结果,使用局部处理的结果在人工数据集上(图2)与全局处理并无明显差异。但是在局部算法中并不能彻底发挥NJW算法的稳定性优势。
4.2. 评价标准
由于三支聚类的特殊性,需要将原本二支聚类评价指标进行修改,使其可以对三支聚类的结果进行正确评价,本指标利用S_Dbw(c) [6] 指标的衡量方法,分别对核心域,边界域进行评价,将两者结果与原本的离散程度进行对比。
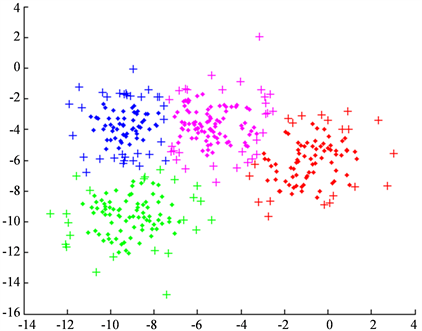
Figure 2. A synthetic data set with 400 points
图2. 包含400个数据的人工数据集
(4)
其中c为二支聚类结果中的类簇个数,S为数据集。 的方差,其p阶距定义如下:
(5)
(6)
是类簇 的方差:
(7)
对 的定义为:如果x是一个向量,则
(8)
记 , , ,其中P为每个已划分类簇核心域构成的集合,B为每个已划分类簇边界域构成的集合,C为原二支聚类的结果。根据Scat(c)指标,从理论上可以得出
,
,
,
. (9)
Table 1. UCI data sets used in experiments
表1. UCI数据集
Table 2. Results of experiments
表2. 实验结果
4.3. UCI数据集测试
本节使用5组UCI数据集Pima (Pi),Ecoli_Nor(EN),Congressional Voting(CV),Iris_Nor(IN),Diabetic Retinopathy Debrecen (DRD)对所算法进行测试。
数据介绍如表1。
实验结果如表2。
从实验结果来看,符合理论预期结果。该算法较好的解决了三支聚类分析中边界域和核心域的划分问题。
5. 总结
通过对每个元素进行加权处理获得个体对全体的影响,确定对象所属区域。思想来源于物理中质心的概念。最后使用S_Dbw(c)进行离散度判断,确定算法的有效性。下一步工作将处理扰动系数,标准扰动量等参数具体的关系,从定性转化为定量分析。更换判定方式,诸如密度等,从而克服维数过高导致的结果不可知。
基金项目
本文受国家自然科学基金(61503160,61572242),江苏省高校自然科学基金(15KJB110004),江苏科技大学本科生创新计划项目资助。
文章引用
王晓磊,王平心. 一种基于扰动分析的三支谱聚类算法
A Three-Way Spectral Clustering Algorithm Based on Perturbation Analysis[J]. 应用数学进展, 2017, 06(08): 985-991. http://dx.doi.org/10.12677/AAM.2017.68118
参考文献 (References)
- 1. Jain, A.K., Murty, M.N. and Flynn, P.J. (1999) Data Clustering: A Review. ACM Computing Survey, 31, 264-323. https://doi.org/10.1145/331499.331504
- 2. Anderberg, M.R. (1973) Cluster Analysis for Application. Academic Press, New York.
- 3. Omran, M.G.H., Engelbrecht, A.P. and Salman, A. (2007) An Overview of Clustering Methods. Intelligent Data Analysis, 11, 583-605.
- 4. Xu, R. and Wunsch, D. (2005) Survey of Clustering Algorithms. IEEE Transactions on Neural Networks, 16, 645- 678. https://doi.org/10.1109/TNN.2005.845141
- 5. 孙吉贵, 刘杰, 赵连宇. 聚类算法研究[J]. 软件学报, 2008, 19(1): 48-61.
- 6. Halkidi, M. and Vazirgiannis, M. (2002) Clustering Validity Assessment: Finding the Optimal Partitioning of a Data Set. Proceedings IEEE International Conference on Data Mining, 29 November-2 December 2001. http://ieeexplore.ieee.org/abstract/document/989517/
