Advances in Applied Mathematics
Vol.
07
No.
12
(
2018
), Article ID:
27985
,
6
pages
10.12677/AAM.2018.712179
New Traveling Wave Solutions for Boiti-Leon-Pempinelle Equation
Peiyuan Yi
South China University of Technology, Guangzhou Guangdong
Received: Nov. 16th, 2018; accepted: Dec. 6th, 2018; published: Dec. 13th, 2018

ABSTRACT
This paper is concerned with smooth and non-smooth traveling wave solutions of the Boiti-Leon- Pempinelle equation based on the bifurcation method of dynamical systems. First, we establish a new Hamiltonian function on the variable u(x, t). Second, we prove that the corresponding traveling wave system of the Boiti-Leon-Pempinelle equation exists new traveling wave solutions. Our work extends some previous results.
Keywords:Boiti-Leon-Pempinelle Equation, Hamiltonian Function, Bifurcation Method, Heteroclinic Orbits
Boiti-Leon-Pempinelle方程新的行波解
易培源
华南理工大学,广东 广州
收稿日期:2018年11月16日;录用日期:2018年12月6日;发布日期:2018年12月13日

摘 要
本文基于动力系统的分支理论对Boiti-Leon-Pempinelle方程的平滑和非平滑的行波解进行研究。首先,我们构建了关于变量u(x,t)的哈密顿函数。其次,我们证明了Boiti-Leon-Pempinelle方程存在着新的行波解。本文的研究扩展了之前相关的研究工作。
关键词 :Boiti-Leon-Pempinelle方程,哈密顿函数,分支理论,异宿轨

Copyright © 2018 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
在本文中,我们研究Boiti-Leon-Pempinelle (BLP)系统
(1.1)
的行波解。Boiti等人 [1] 首先建立了BLP系统的可积性。之后,文献 [2] - [13] 给出了许多不同的行波解。但因为没有考虑到BLP系统所对应的行波系统的所有分支相图,这些文献所求出来的行波解并不完整。本文也将基于行波变换
(1.2)
来研究系统(1.1)的其他行波解,其中c表示波速。将变换(1.2)代入系统(1.1),得到
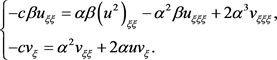 (1.3)
(1.3)
对系统(1.3)的第一个等式对 进行两次的积分,得
(1.4)
令 ,则(1.4)可简化为
(1.5)
从(1.3)第二个等式可以得到
(1.6)
因此,我们对方程(1.5)进行求导,可得
(1.7)
再将等式(1.5)和(1.7)代入(1.6),得到
(1.8)
利用 ,则系统(1.8)改写成如下形式
(1.9)
它的首次积分为
(1.10)
其中h是积分常数。
本文的主要目的就是通过动力系统的分支理论 [14] [15] [16] [17] 来研究系统(1.1)的行波解。我们的贡献包括如下三点:
1) 本文在函数 之上建立了系统(1.1)一个新的哈密顿函数。
2) 基于定性理论和哈密顿函数,我们证明了该系统异宿轨的一个有趣现象,即异宿轨的存在与积分常数g无关。
3) 应用动力系统的分支理论,我们得到了系统(1.1)的平滑和非平滑行波解的精确表达式。
2. 主要结论
在本节,我们列出了BLP方程的平滑和非平滑行波解。为方便起见,先定义如下
定理2.1:当 时,系统(1.1)的精确行波解如下:
1) 三个周期波解
(2.1)
(2.2)
(2.3)
2) 三个扭结波解
(2.4)
(2.5)
(2.6)
3. 理论推导
现在,我们先讨论由首次积分(1.10)所确定的水平曲线的动态。令
(3.1)
有三个零点 (如图1),由下式给出
(3.2)
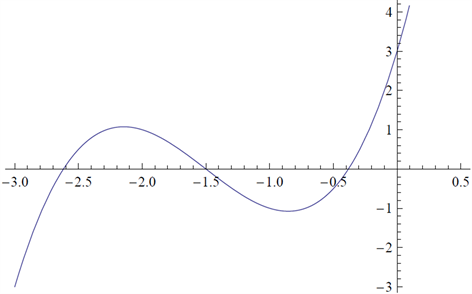
Figure 1. The figure of for and
图1. 在 且 时的图像
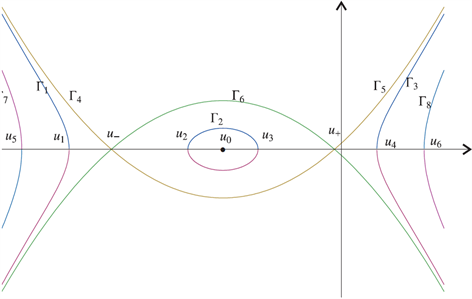
Figure 2. The phase portrait of the BLP equation
图2. BLP方程的相图
由(1.1)的相图(如图2),可以看出,存在通过点 的轨道 。它的轨道的显式表达式为
(3.3)
其中, , , ,且 。
再将(3.3)代入 ,并沿着 进行积分,我们得到
(3.4)
通过查找积分表得到行波解(2.1)。
同理,我们可以继续沿着轨道 进行积分,并得到相应的行波解(2.2)~(2.6)。
4. 结论
本文我们通过动力系统的分支理论证明了行波的存在并证明了扭结波的存在性不受波速和积分常数的影响。同时我们发现一个新的不同于参考文献 [2] 中的哈密顿函数,并得到新的行波解。
从这个意义上讲,我们丰富了Boiti-Leon-Pempinelle方程的性质,并证明了所涉及方法的适用性。
文章引用
易培源. Boiti-Leon-Pempinelle方程新的行波解
New Traveling Wave Solutions for Boiti-Leon-Pempinelle Equation[J]. 应用数学进展, 2018, 07(12): 1537-1542. https://doi.org/10.12677/AAM.2018.712179
参考文献
- 1. Boiti, M., Leon, J.J.-P. and Pempinelli, F. (1987) Integrable Two-Dimensional Generalization of the sine and sinh- Gordon Equations. Inverse Problems, 3, 37-49. https://doi.org/10.1088/0266-5611/3/1/009
- 2. Li, J. and Zhang, Y. (2011) Bifurcations and Parametric Representations of Traveling Wave Solutions for the (2+1)- Dimensional Boi-ti-Leon-Pempinelle System. Mathematical Methods in the Applied Sciences, 34, 147-151. https://doi.org/10.1002/mma.1341
- 3. Wazwaz, A.M. and Mehanna, M.S. (2010) A Variety of Exact Travelling Wave Solutions for the (2+1)-Dimensional Boiti-Leon-Pempinelli Equation. Applied Mathematics and Computation, 217, 1484-1490. https://doi.org/10.1016/j.amc.2009.06.024
- 4. Huang, D.J. and Zhang, H.Q. (2004) Exact Travelling Wave So-lutions for the Boiti-Leon-Pempinelli Equation. Chaos, Solitons and Fractals, 22, 243-247. https://doi.org/10.1016/j.chaos.2004.01.004
- 5. Feng, W.G., Li, K.M., Li, Y.Z. and Lin, C. (2009) Explicit Exact Solutions for (2+1)-Dimensional Boiti-Leon-Pempi- nelli Equation. Communications in Nonlinear Science and Numerical Simulation, 14, 2013-2017. https://doi.org/10.1016/j.cnsns.2008.06.005
- 6. Yang, Z., Ma, S.H. and Fang, J.P. (2011) Soliton Excitations and Chaotic Patterns for the (2+1)-Dimensional Boiti-Leon-Pempinelli System. Chinese Physics B, 20, 107-111. https://doi.org/10.1088/1674-1056/20/6/060506
- 7. Lu, Z.S. and Zhang, H.Q. (2004) Chaos, Soliton Like and Multi-Soliton Like Solutions for the Boiti-Leon-Pempinelli Equation. Chaos, Solitons and Fractals, 19, 527-531. https://doi.org/10.1016/S0960-0779(03)00104-8
- 8. Ren, Y.J., Liu, S.T. and Zhang, H.Q. (2007) A New Gener-alized Algebra Method and Its Application in the (2+1) Dimensional Boiti-Leon-Pempinelli Equation. Chaos, Solitons and Fractals, 32, 1655-1665. https://doi.org/10.1016/j.chaos.2006.01.096
- 9. Cao, J., Song, M. and Zhou, J.S. (2012) New Exact Solutions for the (2+1) Dimensional Boiti-Leon-Pempinelli Equation. International Journal of Mathematical Analysis, 43, 2141-2146.
- 10. Ma, W.X. (2003) Diversity of Exact Solutions to a Restricted Boiti-Leon-Pempinelli Dispersive Longwave System. Physics Letters A, 319, 325-333. https://doi.org/10.1016/j.physleta.2003.10.030
- 11. 郑春龙, 方建平, 陈立群. (2+1)维Boiti-Leon-Pempinelle系统的钟状和峰状圈孤子[J]. 物理学报, 2005, 54(4): 1468-1475.
- 12. Garagash, T.I. (1994) Modification of the Painlev Test for Systems of Nonlinear Partial Differential Equations. Theoretical and Mathematical Physics, 100, 1075-1081. https://doi.org/10.1007/BF01018572
- 13. Jiang, Y., Tian, B., Liu, W.J., Li, M., Wang, P., Sun, K., et al. (2010) Baklund Transformation and Lax Pair for the (2+1)-Dimensional Boiti-Leon-Pempinelli Equation for the Water Waves. Journal of Mathematical Physics, 51, 093519. https://doi.org/10.1063/1.3489865
- 14. Liu, Z.R. and Qian, T.F. (2001) Peakons and Their Bifurcation in a Gen-eralized Camassa-Holm Equation. International Journal of Bifurcation and Chaos, 11, 781-792. https://doi.org/10.1142/S0218127401002420
- 15. Song, M., Ahmed, B., Zerrad, E. and Biswas, A. (2013) Do-main Wall and Bifurcation Analysis of the Klein-Gordon Zakharov Equation in (1+2)-Dimensions with Power Law Nonlinearity. Chaos, 23, 033115. https://doi.org/10.1063/1.4816346
- 16. Pan, C.H., Ling, L.M. and Liu, Z.R. (2014) A New Integrable Equation with Cuspons and Periodic Cuspons. Physica Scripta, 89, 105207. https://doi.org/10.1088/0031-8949/89/10/105207
- 17. Pan, C.H. and Liu, Z.R. (2015) Infinitely Many Solitary Waves of an Integrable Equation with Singularity. Nonlinear Dynamics, 83, 1-7.