Advances in Applied Mathematics
Vol.
08
No.
04
(
2019
), Article ID:
29801
,
7
pages
10.12677/AAM.2019.84072
Boundedness in the Higher-Dimensional Chemotaxis-Growth System with Indirect Attractant Production
Qingquan Tang, Qiao Xin*
College of Mathematics and Statistics, Yili University, Yining Xinjiang

Received: Mar. 31st, 2019; accepted: Apr. 15th, 2019; published: Apr. 22nd, 2019

ABSTRACT
This paper deals with the following Chemotaxis-growth system of the Mountain Pain Beetle with indirect attractant production: in a smoothly bounded domain , is positive. The energy method and Moser iteration are used to prove that under any sufficiently smooth initial boundary conditions, when is large enough, the model has a unique global-in-time classical solution.
Keywords:Indirect Signal Production, Chemotaxis, Logistic Source, Boundedness

具有间接吸引信号产出的高维趋化增长系统解的有界性
唐清泉,辛巧*
伊犁师范大学数学与统计分院,新疆 伊宁

收稿日期:2019年3月31日;录用日期:2019年4月15日;发布日期:2019年4月22日

摘 要
本文考虑一个具有间接信号产出的山松甲壳虫趋化增长系统: ,其中 是一个光滑有界区域, 。利用能量方法和Moser迭代证明了在任意充分光滑的初值边界条件下,当 足够大,该模型有唯一的全局有界经典解。
关键词 :间接信号产出,趋化性,Logistic源,有界性

Copyright © 2019 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
本文考虑了具有间接信号产生的趋化增长模型:
(1.1)
其中 是一个光滑有界区域, 。 表示飞行甲壳虫的密度, 表示做窝甲壳虫释放的化学信号浓度, 表示做窝甲壳虫的密度。山松甲壳虫的模型最早由Strohm,Tyson和Powell [1] 提出,该模型是为了研究山松甲壳虫的趋化行为。趋化行为是指由化学信号浓度梯度引起细胞的偏向运动,细胞偏向于朝化学信号浓度增加的地方移动 [2] [3] [4]。著名的趋化模型是由Keller-Segel于1970年提出 [5] ,具体表示为:
其中 是一个光滑有界区域, 表示细胞密度; 表示细胞产生的化学信号浓度。Keller-Segel模型中的化学信号是由细胞直接产出的,不同于Keller-Segel模型的是模型(1.1)飞行的甲壳虫在松树上做窝产卵变为做窝的甲壳虫产出 [6]。
当
,
时,Hu和Tao在文献 [7] 中证明了模型解的全局有界性。本文证明了
,
时,模型(1.1)解的全局有界性,其中
,
,
满足(3.7),(3.11),(3.9)。当
时,Li和Tao [8] 研究了logistic源为
时的情况,系数满足
时模型解的全局有界性,维数
时,显然
,而本文
优于其结果。在Hu和Tao研究的基础上,Qiu,Mu和Wang [9] 将飞行甲壳虫的随机扩散项
用非线性函数
来描述,考虑扩散系数
对模型的影响,当
时,假设扩散系数
得到
时模型解的全局有界性。而当
时,本文
优于其结果。当
时,Zheng在文献 [10] 中假设扩散系数
得到
时模型解的全局有界性。但是本文
时 是文献 [10] 的一个临界情况。
是文献 [10] 的一个临界情况。
本文在证明解的全局有界性时,先建立 和 一致先验估计,再建立飞行甲壳虫 的 一致估计,再由Moser迭代推得 的 一致有界性,进而根据抛物型方程Neumann边值问题的正则性理论推得 和 的一致有界性。具体地说,有以下结果。
定理1: ,假设 , , , , , 和 。存在唯一的非负函数 :
在 是模型(1.1)的经典解。特别的,存在一个常数 ,使得
, 和 , 。
2. 先验估计
为了证明定理1结果,首先介绍两个基本引理用于主要结论的证明。
引理1:假设 , ,则存在正常数 使得
。
证明:在文献 [10] 中的引理2.7中有详细的证明过程。
要证明模型(1.1)的解全局有界,关键要建立 和 的一致先验估计。
引理2:假设 ,对于任意 ,存在正常数 ,使得模型(1.1)的解 满足
, 和 。
证明:Hu和Tao在文献 [7] 中的引理2.2和引理4.4中证明了 和 的有界性。由 的有界性可以得到 ,从而利用Horstmann和Winkler在文献 [11] 中的引理4.1得到 ,其中 。
3. 主要结论的证明
根据引理2中的先验估计,我们下面利用引理1和Young不等式来估计 的 , 的 和 的 的有界性。
引理3:设 ,若 足够大,则对于任意的 ,存在正常数 使得趋化模型(1.1)的解 满足
, 和 。
证明:第一步:对于任意的 ,利用 和趋化模型(1.1)的第二个方程,经过简单的直接计算可得
(3.1)
对于等式(3.1)中的I项,取 ,则由 紧嵌入在 可得
, (3.2)
进一步,通过Gagliardo-Nirenberg不等式和 的有界性,则存在 使得
,
联合不等式(3.2)可得
 。 (3.3)
。 (3.3)
此外,对于等式(3.1)中的II项,利用Young不等式可知
(3.4)
另一方面,对于等式(3.1)中的III项,利用估计 和Young不等式可得
。 (3.5)
最后,利用Young不等式和引理1可得
(3.6)
联合不等式(3.1)和(3.3)~(3.6)可得
(3.7)
其中 。
。
第二步:为了处理不等式(3.7)右端的项 ,对趋化模型(1.1)的第三个方程乘以 并在 上进行积分并利用Young不等式可得
, (3.8)
即
。 (3.9)
其中 。
第三步:为了处理不等式(3.9)右端的项 ,对趋化模型(1.1)的第一个方程乘 并在 上进行积分可得
(3.10)
对于等式(3.10)右端的第一项,应用Young不等式和引理1可得
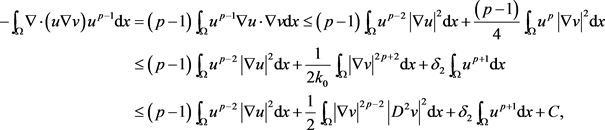
其中 。进而可得
(3.11)
现在,由(3.7) + (3.9) + (3.11)可得
其中 是任意给定的小常数。若 ,则利用Young不等式和Gronwall不等式可得
, 和 。
事实上,若引理3中的 ,则由抛物型方程Neumann边值问题的正则性理论 [12] 可得如下结论。
引理4:设 是趋化模型(1.1)的解,若 足够大,那么对于任意的 ,都存在一个常数 使得
。
在引理3和引理4的基础上,我们有如下的结论。
引理5:若 , 和 是非负的,若 足够大,那么对于任意的存在 ,存在常数 ,使得
和 。
证明:对于任意的
,对趋化模型(1.1)的第一个方程两边同时乘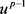 并在
进行积分,然后借助于Young不等式和引理4,容易得到
并在
进行积分,然后借助于Young不等式和引理4,容易得到
这样利用Young不等式可得
,
进一步利用Gronwall不等式可得证
。
那么在引理4和引理5的基础上,运用标准的Alikakos-Moser迭代 [13] 可得证
。
最后利用趋化模型(1.1)第三个一阶线性常微分方程的解,显然可得
。
从而定理1得证。
注1:本文在 足够大的条件下证明了方程解的全局有界性,事实上,若Logistic源项变为 ,从引理3的证明可以看出,当 时,对任意 趋化模型的解全局存在,证明过程只需要简单修改即可。
基金项目
自治区青年科技创新人才培养项目“偏微分方程理论及其在图像处理中的应用”(2017Q081)。
文章引用
唐清泉,辛 巧. 具有间接吸引信号产出的高维趋化增长系统解的有界性
Boundedness in the Higher-Dimensional Chemotaxis-Growth System with Indirect Attractant Production[J]. 应用数学进展, 2019, 08(04): 650-656. https://doi.org/10.12677/AAM.2019.84072
参考文献
- 1. Strohm, S., Tyson, R.C. and Powell, J.A. (2013) Pattern Formation in a Model for Mountain Pine Beetle Dispersal: Linking Model Predictions to Data. Bulletin of Mathematical Biology, 75, 1778-1797. https://doi.org/10.1007/s11538-013-9868-8
- 2. Calvez, V. and Perthame, B. (2006) A Lyapunov Function for a Two-Chemical Species Version of the Chemotaxis Model. BIT Numerical Mathematics, 46, 85-97. https://doi.org/10.1007/s10543-006-0086-8
- 3. Dillon, R., Maini, P.K. and Othmer, H.G. (1994) Pattern For-mation in Generalised Turing systems I. Steady-State Patterns in Systerms with Mixed Boundary Conditions. Journal of Mathematical Biology, 32, 345-393. https://doi.org/10.1007/BF00160165
- 4. Tuval, I., Cisneros, L., Dombrowski, C., Wolgemuth, C.W., Kessler, J.O. and Goldstein, R.E. (2005) Bacterial Swimming and Oxygen Transport near Contact Lines. Proceedings of National Academy of Science of the United States of America, 102, 2277-2282. https://doi.org/10.1073/pnas.0406724102
- 5. Keller, E.F. and Segel, L.A. (1970) Initation of Slime Mold Ag-gregation Viewed as an Instability. Journal of Theoretical Biology, 26, 399-415. https://doi.org/10.1016/0022-5193(70)90092-5
- 6. Parnter, K.J. (2009) Continuous Models for Cell Migration in Tissues and Applications to Cell Sorting via Differential Chemotaxis. Bulletin of Mathematical Biology, 71, 1117-1147. https://doi.org/10.1007/s11538-009-9396-8
- 7. Hu, B.R. and Tao, Y.S. (2016) To the Exclusion of Blow-Up in a Three-Dimensional Chemotaxis-Growth Model with Indirect Attraction Production. Mathematical Models and Methods in Applied Sciences, 26, 2111-2128. https://doi.org/10.1142/S0218202516400091
- 8. Li, H.Y. and Tao, Y.S. (2017) Boundedness in a Chemotaxis System with Indirect Singal Production and Generalized Logistic Source. Applied Mathematics Letters, 77, 108-113. https://doi.org/10.1016/j.aml.2017.10.006
- 9. Qiu, S.Y., Mu, C.L. and Wang, L.C. (2018) Boundedness in the Higher-Dimensional Quasilinear Chemotaxis-Growth System with Indirect Attractant Production. Computers & Mathematics with Applications, 75, 3213-3223. https://doi.org/10.1016/j.camwa.2018.01.042
- 10. Zheng, J. (2018) Global Solvability and Boundedness in the N-Dimensional Quasilinear Chemotaxis Model with Logistic Source and Consumption of Chemoattractant.
- 11. Dirk, H. and Winkler, M. (2005) Boundedness vs. Blow-Up in a Chemotaxis System. Journal of Differential Equations, 215, 52-107. https://doi.org/10.1016/j.jde.2004.10.022
- 12. Ladyzenskaja, O.A. (1968) Linear and Quasilinear Equa-tions of Parabolic Type. In: Translations of Mathematical Monographs, 23.
- 13. Alikakos, N.D. (1979) Bounds of Solutions of Reaction-Diffusion Equations. Communications in Partial Differential Equations, 4, 827-868. https://doi.org/10.1080/03605307908820113
NOTES
*通讯作者。