Advances in Applied Mathematics
Vol.
10
No.
04
(
2021
), Article ID:
41610
,
12
pages
10.12677/AAM.2021.104097
一类金融动力系统的Lyapunov指数计算及混沌动力学分析
王雪歌,黄东卫
天津工业大学,数学科学学院,天津

收稿日期:2021年3月14日;录用日期:2021年4月3日;发布日期:2021年4月16日

摘要
本文对一类金融混沌系统进行动力学分析,利用软件Mathematica编写程序计算不同参数下的Lyapunov指数,绘制相图,分岔图。数值模拟验证了理论分析,使分析更加全面;分析表明参数的选取对于调控金融混沌系统极其重要。本文的研究为此类经济系统的决策提供了一些参考。
关键词
Lyapunov指数计算,分岔图,相图,软件Mathematica
Lyapunov Exponent Calculation and Chaotic Dynamics Analysis for a Kind of Financial Dynamic System
Xuege Wang, Dongwei Huang
School of Mathematical Sciences, Tianjin Polytechnic University, Tianjin

Received: Mar. 14th, 2021; accepted: Apr. 3rd, 2021; published: Apr. 16th, 2021

ABSTRACT
In this paper, dynamics analysis is carried out on a kind of financial chaotic system. Mathematica is used to write a program to calculate Lyapunov exponent under different parameters and draw phase diagram and bifurcated diagram. The numerical simulation verifies the theoretical analysis and makes the analysis more comprehensive. The analysis shows that the choice of parameters is very important for the regulation of financial chaos system. The research in this paper provides some references for the decision-making of such economic system.
Keywords:Lyapunov Exponent Calculation, Bifurcation Diagram, Phase Diagram, Software Mathematica

Copyright © 2021 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
金融系统是有关资金流动、集中和分配的一个体系,包括股票、债券和其他证券的市场,还包括银行和保险公司等金融中介机构。物价结构、供求关系与利率等因素的相互影响,使得很多金融问题变得复杂,如金融市场常会出现停滞、失控、甚至引发金融危机等现象。面对复杂的金融系统,深入地研究其内部结构,揭示金融系统发展规律和控制系统的混沌状态,这显得尤为重要。很多学者已经研究了一些非线性金融学模型,文献 [1] 提出了经典的金融系统(1),文献 [2] [3] 给出了其动力学分析。经典金融系统数学表达式如下:
(1)
文献 [4] [5] [6] [7] 分别在经典的金融系统的基础上进行了改进,并对系统进行动力学分析及控制。文献 [8] [9] [10] 通过建立新的金融系统,对金融系统进行了动力学分析并对控制方法进行了探索研究,使人们对金融系统得到了更深刻的认识。通过研究发现影响利率变化的因素除了投资需求、价格指数外,还与平均利润率有关,且平均利润率与利率成正比例关系,文献 [11] 基于此关系对混沌金融系统(1)进行了改进,对改进之后的系统加入控制之后的状态特性进行了讨论。
前人对此系统并未计算不同参数下的Lyapunov指数,本文计算了不同参数之下的Lyapunov指数,把Lyapunov指数、相图、分岔图结合起来对改进后的金融混沌系统进行动力学分析,并使用四阶Rung-Kutta法对系统进行离散,利用QR分解方法 [12] [13],使用软件Mathematica编程计算Lyapunov指数 [14],根据Lyapunov指数的正负判断系统的稳定性。最后进行数值模拟,绘制系统的相图、随着参数改变的分岔图,对系统进行多方位分析.本文的目的是通过对金融混沌系统的动力学分析之后,可以为此类的经济系统的调控提供一些参考,为经济系统的稳定运行提供新的思路。
2. 金融系统
考虑平均利润率与利率成正比例关系,文献 [8] 对系统(1)的第一个方程进行了改进,得到了改进的金融混沌系统:
(2)
其中x代表利率,y代表投资需求,z代表价格指数,a表示储蓄量,b表示单位投资成本,c表示商品需求弹性,k为控制参数。a、b、c、k均为正数。当 ,,, 时,此系统呈现混沌。
3. 理论分析
3.1. 对称性和不变性
用 替换系统(2)中的 ,方程保持不变,系统关于y轴是对称的。即若 是系统的解,则 也是系统的解。换言之,所有的解要么是本身,要么是其对称解。
3.2. 耗散性和吸引子
对于系统(2),其散度为:
当散度 时,即 时,系统是耗散的,相空间的体积按指数形式 快速缩小。保证了吸引子是存在的。
3.3. 平衡点和稳定性
求系统(2)的平衡点,令:
(3)
当 时,系统有唯一平衡点E1;
当 时,系统有三个平衡点E1、E2、E3分别为:
下面讨论其平衡点的稳定性:
在平衡点E1处的Jacobi矩阵为
令其特征方程等于零:
对应的三个特征根为: , 是下列方程的解:
因为 ,故 。分以下几种情况讨论平衡点的稳定性。
1) 当 时,特征方程 的特征根 均小于0,系统有唯一平衡点E1,且平衡点E1是稳定的汇;
2) 当 时, ,结合 ,故此时平衡点E1是鞍点;
3) 当 时, 和 是一对纯虚根,结合 ,取 ,则 满足Hopf分岔的横截条件,说明当a通过a0时系统的轨道横穿虚轴,此时系统的平衡点E1发生Hopf分岔;
4) 当 时,则 ,结合 ,分成两种情况:
a) 若 ,即 ,此时平衡点E1为非双曲的不稳定平衡点;
b) 若 ,即 ,由中心流行定理可判断平衡点E1为渐进稳定的。
在条件(4)的情况下,平衡点E1由不稳定变为稳定的,所以当 时,系统在平衡点E1处发生了跨临界分岔。
5) 当 时,系统有三个平衡点为:E1,E2,E3,此时平衡点的情况较复杂,由于篇幅问题,暂不展开。
4. Lyapunov指数
Lyapunov指数是指在相空间中两条邻近轨道随着时间的推移按指数方式相互分离或靠拢的速率。混沌系统的一个最重要的特征是对初始值的敏感依赖性,Lyapunov指数正是对这一敏感依赖性的量化。当一个系统的Lyapunov指数出现正值时,此系统是混沌的。
对于n维离散动力系统 ,设 是该系统的一条轨道, 为偏离该轨道的一微小量。则 的演化满足 ,其中 为F在 处的Jacobian矩阵。可以得到 。记 ,则 。设 ,则 是一个正定矩阵。设 为 的n个特征值。则n维离散系统的第 个Lyapunov指数: 。
对于n维连续动力系统 ,其中 ,,。那么n维连续动力系统的第i个Lyapunov指数 可以表示为:
在本文中,先使用四阶Runge-Kutta法对金融混沌系统进行离散,再按照离散系统的QR分解方法计算Lyapunov指数。对定义的 进行QR分解,在Mathematica中编写程序计算Lyapunov指数。
我们考虑参数对系统的影响,使用控制变量法。我们计算系统在不同参数值下的Lyapunov指数,根据Lyapunov指数判断系统在不同参数下的稳定性。
1) 固定参数 ,改变参数a, ,初值取为: ,在 附近给不同的a值,计算不同参数值下系统的Lyapunov指数。
Table 1. A list of cases in which the Lyapunov exponent varies with parameter a
表1. 李雅普诺夫指数随参数a变化的情况列表
由表1计算的Lyapunov指数可以看出,固定参数 ,改变参数a,当 与 时,系统的最大Lyapunov指数大于0,说明在这样的参数取值下,系统呈现混沌状态;固定参数 ,参数 时,系统的Lyapunov指数均小于0。此时系统处于稳定状态。
2) 固定参数 ,改变参数c, ,初值取为: ,在 附近取不同的c值,计算不同参数值下系统的Lyapunov指数。
Table 2. A list of cases in which the Lyapunov exponent varies with parameter c
表2. 李雅普诺夫指数随参数c变化的情况列表
由表2的Lyapunov指数可以看出,系统在固定参数a, b, k的情况下,参数 的时候,系统的Lyapunov指数均小于0,系统是稳定的;当参数c取1.8, 1.9, 2.1, 2.2, 2.3, 2.4, 2.5的时候,系统的最大Lyapunov指数均大于0,故在这样的参数取值下,系统呈现混沌状态。
5. 数值模拟
5.1. 时间范围对系统的影响
当参数取 时,初值为: 。在参数取上述值时,利用Mathematica计算系统的Lyapunov指数为: ,可以看到系统的最大Lyapunov指数大于0,说明此时系统呈现混沌状态的。
考虑时间范围的长短对系统混沌状态的影响,分别取时间 ,,使用Mathematica绘制相图,观察二者区别。
1) 当时间 时,可得如下相图(图1):
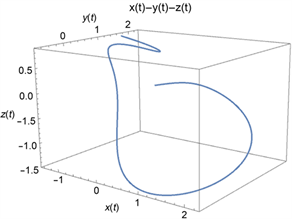
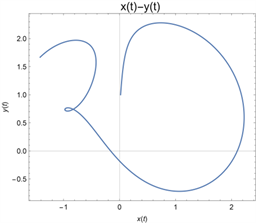


Figure 1. t belongs to the phase diagram in the range of (0,11)
图1. 时的相图
2) 当时间 时,可得如下相图(图2):
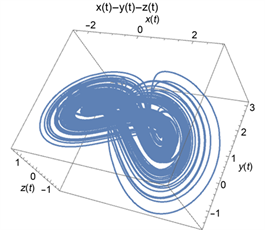



Figure 2. t belongs to the phase diagram in the range of (0,10000)
图2. 时的相图
由相图可以看出:时间越长,这个系统的混沌特性越明显。
5.2. 参数对系统的影响
本小节基于控制变量法画出x随着参数a变化的分岔图以及x随着参数c变化的分岔图。第三节已经求出不同参数取值下的Lyapunov指数,本小节绘制相对应参数下的相图,结合起来对系统进行全方位的分析。
1) 固定参数 ,改变参数a, ,利用Mathematica编程画出x随着a变化的分岔图,如图3所示。由分岔图可知,系统在 之间大部分处于混沌状态,在 之间处于稳定状态。
系统在 附近发生变化,分别画出 时的相图,如图4~8。当a取3.8和3.9时,取时间 ,由图4、图5可知,系统是不稳定的,与Lyapunov指数判断系统是混沌的结论是一致的。当 时,相图表明系统是稳定的。与Lyapunov指数计算所得到的结论是一致的。
2) 固定参数 ,改变参数c, ,得到系统x随着c变化的分岔图如图9所示,由分岔图知,系统在 时系统大部分处于混沌状态,随着c的增加,混沌状态越来越不明显。由分岔图可看出系统在 附近状态发生了变化。画出系统取以下参数的相图: (图10), (图11), (图12), (图13), (图14)。可以观察到系统取以下参数时: ,系统均呈现混沌状态;在 时,系统处于稳定状态。相图与Lyapunov指数所得到的结论是一致的。
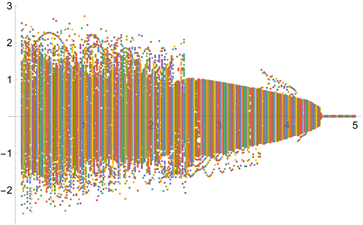
Figure 3. A bifurcation of x with respect to a
图3. x随着a变化的分岔图

Figure 4. Phase diagram at
图4. 时的相图

Figure 5. Phase diagram at
图5. 时的相图
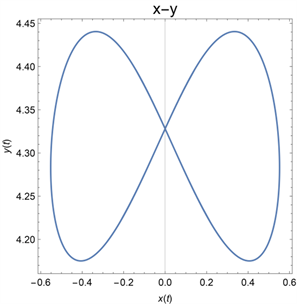
Figure 6. Phase diagram at
图6. 时的相图

Figure 7. Phase diagram at
图7. 时的相图

Figure 8. Phase diagram at
图8. 时的相图

Figure 9. A bifurcation of x with respect to c
图9. x随着c变化的分岔图
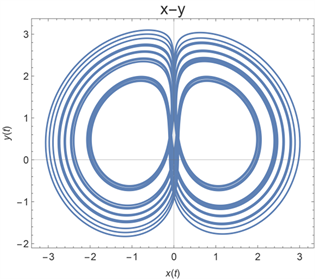
Figure 10. Phase diagram at
图10. 时的相图

Figure 11. Phase diagram at
图11. 时的相图

Figure 12. Phase diagram at
图12. 时的相图

Figure 13. Phase diagram at
图13. 时的相图

Figure 14. Phase diagram at
图14. 时的相图
6. 结论
本文对金融混沌系统进行了动力学分析,并运用Mathematica编写程序进行了Lyapunov指数计算,结合相图、分岔图对系统有了更全面的认识。通过研究发现系统中的参数选定极为重要。储蓄量 越小,系统波动越大,过小还会导致混沌发生;a也不能太大,过大容易导致经济市场缺乏活力。通过本文的分析,为决策机构提供了调控此类金融系统的一些思路,使经济相对稳定。
致谢
全体作者感谢审稿人和编辑的细心指导!
基金项目
国家自然科学基金(11672207);天津市自然科学基金(17JCQNJC03800, 17JCYBJC15700, 18JCYBJC18900)。
文章引用
王雪歌,黄东卫. 一类金融动力系统的Lyapunov指数计算及混沌动力学分析
Lyapunov Exponent Calculation and Chaotic Dynamics Analysis for a Kind of Financial Dynamic System[J]. 应用数学进展, 2021, 10(04): 887-898. https://doi.org/10.12677/AAM.2021.104097
参考文献
- 1. 马军海, 陈予恕. 一类非线性金融系统分岔混沌拓扑结构与全局复杂性研究(I) [J]. 应用数学和力学, 2001, 22(11): 1119-1128.
- 2. 马军海, 陈予恕. 一类金融系统分岔混沌拓扑结构与全局复杂性研究(II) [J]. 应用数学和力学, 2001, 22(12): 1236-1241.
- 3. 黄登仕, 李后强. 非线性经济学的理论和方法[M]. 成都: 四川大学出版社, 1995.
- 4. 雷腾飞, 张艳萍, 胡原野, 杨夏青, 乔石. 一类改进金融混沌系统的动力学分析与自适应同步控制[J]. 嘉应学院学报, 2018, 36(8): 34-40.
- 5. 雷腾飞, 黄丽丽, 夏炎, 代严满. 一类金融系统的混沌机理分析[J]. 济宁学院学报, 2016, 37(6): 13-17.
- 6. 王晶囡, 吕静, 李想. 一类金融系统的分岔分析与混沌[J]. 动力学与控制学报, 2016, 14(6): 508-512.
- 7. 王博, 张晓丹. 一类三维耦合混沌系统的动力学分析与数值模拟[J]. 北京科技大学学报, 2007, 29(6): 636-640.
- 8. Liao, Y., Zhou, Y., Xu, F. and Shu, X.-B. (2020) Complexity Research; A Study on the Complexity of a New Chaotic Financial System. Journal of Technology, 2020, Article ID: 8821156. https://doi.org/10.1155/2020/8821156
- 9. 李博, 刘国欣, 田瑞兰. 金融领域风险系统的混沌动力学行为研究[J]. 技术经济与管理研究, 2021(1): 18-22.
- 10. Lu, X. and Peng, M. (2020) A Financial Chaotic System Control Method Based on Intermittent Controller. Mathematical Problems in Engineering, 2020, Article ID: 5810707. https://doi.org/10.1155/2020/5810707
- 11. 杨明证. 一类改进的混沌金融系统的混沌同步研究[D]: [硕士学位论文]. 镇江: 江苏大学, 2010.
- 12. von Bremen, H.F., Udwadia, F.E. and Proskurowski, W. (1997) An Efficient QR Based Method for the Computation of Lyapunov Exponents. Physica D: Nonlinear Phenomena, 101, 1-16. https://doi.org/10.1016/S0167-2789(96)00216-3
- 13. 张晓丹, 李志萍, 张丽丽. 一类基于奇异值分解的Lyapunov指数计算方法[J]. 北京科技大学报, 2005, 27(3): 371-374.
- 14. 张伯俊, 王谦, 黄东卫. 用Lyapunov指数分析物理双摆的混沌特征[J]. 天津工业大学学报, 2014, 33(2): 85-88.
