Advances in Applied Mathematics
Vol.
12
No.
05
(
2023
), Article ID:
65213
,
5
pages
10.12677/AAM.2023.125217
函数 所确定的Wulff形
周小静,蓝一涵
贵州师范大学数学科学学院,贵州 贵阳
收稿日期:2023年4月11日;录用日期:2023年5月6日;发布日期:2023年5月12日

摘要
凸体是积分几何和凸几何分析的重要内容,Wulff形作为一类特殊凸体,具有一定研究价值。利用凸体的支持函数与函数性质,研究函数 所确定的Wulff形,给出Wulff形的周长和面积的计算公式。
关键词
支持函数,正连续函数,Wulff形

Wulff Shape Determined by the Function
Xiaojing Zhou, Yihan Lan
Department of Mathematical Sciences, Guizhou Normal University, Guiyang Guizhou
Received: Apr. 11th, 2023; accepted: May 6th, 2023; published: May 12th, 2023

ABSTRACT
Convex body is an important part of integral geometry and convex geometry analysis. As a special convex body, Wulff shape has certain research value. By using the support functions of convex bodies and function properties, this paper discusses the Wulff shape determined by the function , given the formula for calculating the perimeter and area of the Wulff shape.
Keywords:Support Function, Positive Continuous Function, Wulff Shape

Copyright © 2023 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言与主要结果
积分几何和凸几何分析研究领域涉及广泛,在计算机软件和力学等方面也有广泛应用,凸体是积分几何和凸几何分析学科中的重要研究对象,Wulff形作为特殊凸体值得我们进一步研究。
记 为 维欧氏平面, 为 中单位球面, 为 中单位圆周。设K为 中点集,如果对任意两点 , ,都有 ,则称K为凸集。具有非空内点的紧凸集称为凸体。
若K为 中的凸体,由文献 [1] 得出其支持函数 的定义为:
其中p是平面直角坐标系 原点o到直线 的距离,u是ox轴与过原点又垂直于G的射线的夹角,且直线 的广义法式方程为:
其中 是直线 上点的坐标。
给出二维欧氏平面 上一个单参数直线族
(1)
其中 是参数。当 的值变化时,得到族中不同的直线 ,并且假定函数 具有一阶与二阶连续偏导数,则有直线族 的包络C满足方程组
(2)
关于包络更详细的定义,参见文献 [2] 。
引理1 设曲线C由参数方程
给出,在 上 连续, 连续可微且 (对于 连续可微且 的情形可类似地讨论)。记 ( 或 ),则由曲线C及直线 和x轴所围成的图形,其面积计算公式为
(3)
假设函数 是严格正连续函数,区间 ,则对给定的 ,称
是关于函数 的Wulff形,且Wulff形是凸体 [3] 。
关于Wulff形的研究已有一些成果。Yi Jun He [4] 借助高斯映射等刻画了Wulff形的新特征;Ai-Jun Li [5] 研究了Wulff形及其极线的截面和投影的体积不等式;Huhe Han [6] 研究了Wulff形和某类凸积分。本文研究对象与其他不同的是选定了一类严格正的特殊连续函数,研究对应Wulff形的形状、周长和面积等。
因函数 中的t对此处的研究无影响,于是记函数 为 ,记Wulff形 为K,其面积记为 ,周长记为 。
在 上,函数 。取 ,实数 ,显然 是严格正的连续函数,所以由它可以确定一个Wulff形。本文研究了函数 所确定的Wulff形的相关问题,得到如下主要结果:
定理1 若函数 ,且实数 ,则该函数所确定的Wulff形是操场域,它的两段圆弧分别以点 和点 为圆心,以a为半径。
2. 定理的证明
定理1的证明 给定函数 ,因为它在定义域区间 上不可导,所以不能直接在 上通过求导来讨论,又因为不可导的点只有 ,于是可将定义域分为 和 两个部分进行考虑。
在区间 上, ,根据直线 的方程是 ,得到直线族 的方程为:
其中 是参数。代入方程组(2) 得
(4)
根据上式解得
进而有
它表示以 为圆心,以a为半径的圆,此圆上的点并不都是Wulff形边界上的点,因为还要考虑
这一限制。在区间 上,当 时, , ;当 时, , ;当
时, , ,Wulff形边界的轨迹是连续的,当u从0到 变化时,满足(4)式的点刚好是以 为圆心,以a为半径的圆的上半圆弧,它参与构成Wulff形的边界。
同理考虑区间 ,因为 ,又根据直线 的方程是 ,得到直线族 的方程为:
其中 是参数。代入方程组(2) 得
(5)
根据上式解得
进而有
它表示以 为圆心,以a为半径的圆。在讨论的区间 上,当 时, , ;
当 时, , ;当 时, , ,Wulff形边界的轨迹是连续的,所以只
有下半圆弧参与构成Wulff形的边界。
再考虑区间端点 。当 时,直线 的方程是 ;当 时,直线 的方程是 ;当 时,直线 的方程是 ,结合Wulff形的定义分析可以知道,直线 和直线 与前面得到的两个半圆弧构成的闭合凸体就是函数 所确定的Wulff形,是一个操场域,它的两段圆弧分别以点 和点 为圆心,以a为半径。
推论1 若函数 ,K是 所确定的Wulff形,则K的周长 ,K的面积 。
证明 因为函数 所确定的Wulff形是由两个半圆和一个矩形组成的操场域,所以通过简单计算容易得到它的面积 ,周长 。
此外,也可以应用公式(3)计算函数 所确定的Wulff形的面积,有
具体取函数 得到图1如下,在函数 中将参数a取为其他值,得到图2如下:
图1中所示Wulff形的面积为:
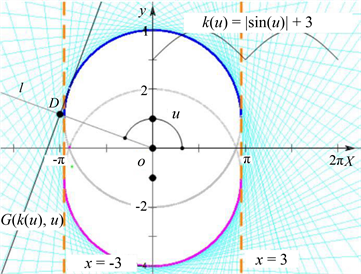
Figure 1. The Wulff shape determined by the function
图1. 函数 所确定的Wulff形
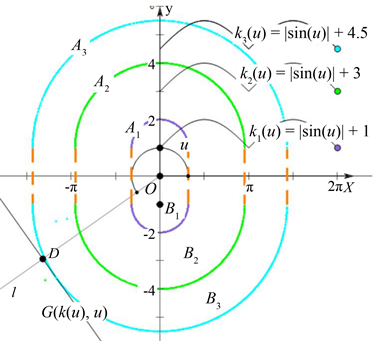
Figure 2. The Wulff shape determined by the function
图2. 函数 所确定的Wulff形
关于函数 所确定的Wulff形是后续的研究内容。基于上述结论,可研究函数 所确定的Wulff形及其相关性质。
文章引用
周小静,蓝一涵. 函数k(u)=▏sinu▏+a所确定的Wulff形
Wulff Shape Determined by the Function k(u)=▏sinu▏+a[J]. 应用数学进展, 2023, 12(05): 2138-2142. https://doi.org/10.12677/AAM.2023.125217
参考文献
- 1. 任德麟. 积分几何引论[M]. 上海: 上海科学技术出版社, 1998.
- 2. 梅向明, 黄敬之. 微分几何[M]. 北京: 高等教育出版社, 2019.
- 3. Böröczky, K.J., Lutwak, E., Yang, D. and Zhang, G.Y. (2012) The Log-Brunn-Minkowski Inequality. Advances in Mathematics, 231, 1974-1997. https://doi.org/10.1016/j.aim.2012.07.015
- 4. He, Y.J. and Li, H.Z. (2008) Integral Formula of Minkowski Type and New Characterization of the Wulff Shape. Acta Mathematica Sinica (English Series), 24, 697-704. https://doi.org/10.1007/s10114-007-7116-6
- 5. Li, A.J., Huang, Q.Z. and Xi, D.M. (2017) Volume Inequalities for Sections and Projections of Wulff Shapes and Their Polars. Advances in Applied Mathematics, 91, 76-97. https://doi.org/10.1016/j.aam.2017.05.010
- 6. Han, H.H. and Nishimura, T. (2017) Strictly Convex Wulff Shapes and C1 Convex Integrands. Proceedings of the American Mathematical Society, 145, 3997-4008. https://doi.org/10.1090/proc/13510