Advances in Applied Mathematics
Vol.
13
No.
02
(
2024
), Article ID:
81451
,
15
pages
10.12677/AAM.2024.132055
关于相关数据流的随机梯度哈密尔顿蒙特卡罗算法的非渐近估计
杨金圆,胡良剑*
东华大学理学院,上海
收稿日期:2024年1月26日;录用日期:2024年2月21日;发布日期:2024年2月28日

摘要
近年来,基于朗之万蒙特卡罗方法的随机梯度下降算法得到了广泛应用。这些算法通过在梯度的估计中注入适当的高斯噪声以实现在非凸优化问题中的全局收敛。随机梯度哈密尔顿蒙特卡罗(SGHMC)是随机梯度下降带有动量的一种变体,通常的研究以样本数据相互独立的假设为前提来分析SGHMC算法的收敛性,然而实际中的样本数据往往存在相关性。本文在数据流具有相关性(满足一定的条件混合特性)的条件下,给出了SGHMC算法的非渐进估计,建立了全局Lipschtiz条件下SGHMC算法的收敛性定理,得到了迭代分布与目标分布之间Wasserstein距离的上界。
关键词
随机梯度哈密尔顿蒙特卡罗,非渐进估计,非凸优化,相关数据流

Non-Asymptotic Estimates for Stochastic Gradient Hamiltonian Monte Carlo Algorithm with Dependent Data Streams
Jinyuan Yang, Liangjian Hu*
College of Science, Donghua University, Shanghai
Received: Jan. 26th, 2024; accepted: Feb. 21st, 2024; published: Feb. 28th, 2024

ABSTRACT
In recent years, stochastic gradient descent algorithms based on the Langevin Monte Carlo method have been widely applied, which achieve global convergence in non-convex optimization problems by injecting appropriate Gaussian noise into the gradient estimates. Stochastic gradient Hamiltonian Monte Carlo (SGHMC) is a variant of stochastic gradient descent with momentum. Usually, studies analyze the convergence of algorithm based on the assumption that the sample data are i.i.d. However, in practice, sample data may be dependent. This paper provides non-asymptotic estimates for SGHMC algorithm under the condition that the data streams are dependent (satisfying a certain conditional mixing property), establishes a convergence theorem for SGHMC algorithm under the global Lipschitz condition, and obtains an upper bound of the Wasserstein distance between the law of algorithm’s iterates and the target distribution.
Keywords:Stochastic Gradient Hamiltonian Monte Carlo, Non-Asymptotic Estimates, Non-Convex Optimization, Dependent Data Streams

Copyright © 2024 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
随机梯度下降算法在解决非凸优化问题中有着广泛应用。考虑一个随机优化问题:
最小化
其中U可能是非凸损失函数,
,X是随机数据。我们希望得到
的估计量
使超额期望风险
达到最小。Raginsky等 [1] 阐述了最小化超额期望风险与从一个集中在损失函数U的极小值附近的目标分布
中采样之间的密切联系,其中
为逆温度系数。当
足够大时,目标分布
集中在损失函数U的极小值附近 [2] ,且在适当的假设下,目标分布
是过阻尼郎之万随机微分方程
(1)
的唯一平稳分布 [3] ,其中
,
为d维布朗运动。
在非凸情形下损失函数U可能具有多个极小值,为算法收敛带来挑战。为了从目标分布
中采样,基于朗之万蒙特卡罗(Langevin Monte Carlo, LMC)方法的随机梯度下降(Stochastic Gradient Descent, SGD)算法备受关注,这些算法通过在梯度的估计中注入噪声保证全局收敛。考虑使用欧拉离散化方法近似模拟方程(1),同时由于精确梯度h难以获得,故使用其以观测数据驱动的无偏估计代替,即得到随机梯度郎之万动力学(Stochastic Gradient Langevin Dynamics, SGLD)算法 [4]
其中
为步长,
为满足
的可测函数,
为适应于给定流
的
值数据序列,
为独立的标准d维高斯噪声。
另一方面,本文所考虑的随机梯度哈密尔顿蒙特卡罗(Stochastic Gradient Hamiltonian Monte Carlo, SGHMC)算法 [5] 基于欠阻尼朗之万随机微分方程
(2)
其中
,
分别为位置和动量过程,
为摩擦系数。在梯度的适当假设下,马尔可夫过程
具有唯一平稳分布 [6]
与SGLD算法类似,精确梯度h难以获得,但可以有效获得其无偏估计,即得到SGHMC算法
(3)
Eberle等 [7] 证明了在某些假设条件下欠阻尼随机微分方程在Wasserstein距离下收敛到其平稳分布的速度比过阻尼情形快,许多实验也印证了SGHMC算法表现出比SGLD算法更快的收敛速度 [5] 。
近年来,损失函数U为凸情形下的近似采样算法的收敛速度得到了深入研究,放宽凸假设是一个更具挑战的问题。对于U非凸的情形,通常考虑两种路径:(i) 考虑耗散条件 [1] [8] ;(ii) 假设损失函数U在无穷远处具有凸性 [9] 。此外,大多数研究假设样本数据序列相互独立,然而事实上数据可能相关而非独立。如金融市场价格分析问题中,资产收益在适当的时间尺度上保持平稳,但独立性失效 [10] 。在下达交易订单以最大化投资组合效益、最小化交易成本等金融问题中,随机梯度下降算法往往在相关数据流的基础上进行 [8] 。Chau等 [8] 在相关数据流(样本数据满足条件L混合特性)假设下研究了非凸情形下SGLD算法的收敛性。对于SGHMC算法,在观测数据独立同分布的假设下,Chau等 [6] 和Gao等 [11] 研究了SGHMC算法在全局Lipschitz条件下的收敛性。本文将考虑的数据样本
是相关的,在数据序列满足条件L混合特性的条件下,得到SGHMC算法的非渐近估计,并由此得到SGHMC算法收敛到其目标分布的速度。
2. 符号与假设
2.1. 符号
设
为一个概率空间。记随机变量X的期望为
,用
表示p阶矩可积的实值随机变量的空间。给定整数
,记
上Borel
代数为
,随机变量X在
上的分布用
表示。记内积为
,相应的范数用
表示。对于
,用
表示中心为0,半径为r的闭球。可测空间
上的概率测度的集合记为
。对
,用
表示
上的概率测度
的集合,其边际分布分别为
。Wasserstein距离定义为
2.2. 假设
假设2.1 损失函数U取非负值,即
。
假设2.2
,
。
假设2.3 设
为代表过去信息的给定流,且
,
。设
为一个递减的
代数族,使得对所有
,
和
相互独立。过程
关于
是条件L混合的,且满足对任意
和
,
(4)
假设2.4 存在正常数
,
,使得对所有
和
,有
(5)
假设2.5 存在正常数a,b使得对所有
和
,
注2.6 由假设 2.4 ,得到以下性质:
(i) 对所有
,
(6)
其中
。
(ii) 对所有
,
(7)
其中
。
3. 主要结果
3.1. 条件L混合
Gerencsér [12] 介绍了L混合过程,L混合表示随机序列中相邻元素间相关性快速减小。Chau等 [13] 在随机梯度方法的背景下引入了条件L混合的概念,条件L混合表示在给定一些信息或条件下序列的混合性质仍然成立。考虑概率空间
,具有离散时间流
和一个递减的
域序列
,使得对所有
,
和
相互独立。当
时,若
,随机过程
称为
有界。
对每个
和
,定义
其中
为
的第i个分量,且设
(8)
定义3.1 (条件L混合) 称随机过程
关于
为条件L混合,如果满足以下条件:
(i) 对所有
,
均为
适应;
(ii) 对所有
,随机过程
为
有界;
(iii) 对所有
,序列
,
为
有界。
由上述定义,若
为独立序列且满足(i)和(ii),则(iii)也成立,可视为条件L混合过程的特殊情况。设
为条件L混合过程,对
引入量
。下面的结论分别来自参考文献 [14] 的定理B.5、引理6.4和例2.4、引理A.3。
定理3.2 对
,设
为
有界,且设
。假设对
,
。设
为
可测,且有
,则存在一个常数
使得
这里可以取
。
引理3.3 若假设2.4成立,则对每个
,
满足
引理3.4 若假设2.4成立,且设
。令
为
值随机变量族,满足
是
可测的。对
,定义过程
,则
3.2. 收敛定理
首先定义
其中常数K1,K2,K3将在引理4.2的证明中给出,常数
和K4将在引理4.3的证明中给出,参数
在(9)中引入。下面给出SGHMC算法到目标分布的收敛性的主要结果。
定理3.5 若假设2.1~2.5成立且
,则存在常数
,使得
其中C1,C2依赖于
,
,d,L1,L2和数据流
,具体形式分别在定理4.6和定理4.8的证明中给出,C3,C4依赖于
,
,d,L1,具体形式在定理3.5的证明中给出。
本文在数据流存在相关性的假设下给出了SGHMC算法的非渐近估计,阐明了SGHMC算法在有限迭代次数n下的性能。定理3.5表明算法的误差在迭代次数n上一致有界且选择足够小的步长
可以使误差达到任意小,从而保证了算法的收敛性在相关数据流情形下依然成立。与独立数据流的情形相比,本文在定理证明过程中采用与文献 [6] 不同的证明路线。本文将SGHMC算法与依赖于条件L混合的辅助过程进行比较,得到相关数据流情形下二者之间的Wasserstein距离。此外,本文在算法的误差估计中得到不同的系数表达式,条件L混合特性为这些系数的有界性提供了保证。
4. 证明
4.1. 辅助过程
证明主要结果的中心思想是引入合适的Lyapunov函数及SGHMC算法的连续时间插值过程等辅助过程,该连续时间插值过程在离散时间下的分布与SGHMC算法相同。不同于SGLD算法中经典的Lyapunov函数
,本文使用Eberle [7] 定义的Lyapunov函数:
(9)
其中
,该函数依赖于目标函数
。
下面定义
的缩放过程
,
(10)
其中
。记
自然流为
,且
与
相互独立,则
自然流记为
且
,
也与
相互独立。此外,记
。
然后定义SGHMC算法(3)的连续时间插值过程:
(11)
注意到,插值过程(11)与SGHMC算法在格点上具有相同的分布,即
。此外,考虑一个初值条件为
和
连续时间过程
:
(12)
定义4.1 给定
且对
,定义过程
(13)
直观看来,过程
是一个开始于时间
且初值为
的欠阻尼Langevin过程。
最后,对
定义一个含样本数据
信息流和布朗运动
随机性的连续时间流
:
4.2. 引理准备
引理4.2 若假设2.1~2.5成立。则对
,
其中
。
证明 设对
,
(14)
类似文献 [15] 中引理3.2的证明,由(3)和注2.6的(6)得到
(15)
其中
(16)
且
,
。注意到对
,由假设2.1,
(17)
由(14)中
的定义及不等式
,得到
(18)
因此,由和,得到
其中
由参考文献 [15] 中的引理B.5,选择
,可得到对所有
,有
(19)
其中
。故将(19)代入(15),得到
(20)
又
时,由(14)得到
(21)
则对
,由(20)和(21),得到
(22)
其中
。结合(17),最终得证。
引理4.3 设
,且假设2.1~2.5成立,则有
其中
为与
无关的常数。
证明 首先,定义
,
。类似参考文献 [15] 引理3.4和文献 [6] 引理5.5的证明,得到
(23)
其中
(24)
下面求(24)中第一式的上界,由(17)和不等式
,有
(25)
其中
将(25)代入(23),对
,整理得到
(26)
其中,
(26)两边平方取条件期望,注意到
,由假设2.3的(4)和注2.6,得到
(27)
其中
且
对于
,由注2.6的(6)和参考文献 [15] 引理3.4的证明,可得到
(28)
其中
将(28)代入(27),利用
,结合(17),得到
(29)
其中
对(29)两边取期望,由于
,有
其中
。由引理4.2的证明过程中的(22)和
,当
时,递归计算得到
其中
,
。
下面给出参考文献 [8] 的引理3.15和引理3.16。
引理4.4 对每个
,存在一个可测函数
使得对任意
和
,
是
的一个版本,且对几乎每个
,
是连续的。
引理4.5 若假设 2.2 和假设 2.3 成立,且设
,则
4.3. 主要结果的证明
为证明主要结果,考虑将证明目标分解成如下形式:
(30)
将证明目标转化为控制(30)右边三项。对给定步长
,将时间轴划分为长度为
的区间。对(30)右边第一项,将比较连续插值过程的分布
与区间上由(13)定义过程的分布之间的距离,二者在区间起点上具有相同初始分布。对(30)右式第二、三项的控制主要依赖于 [7] 中收缩估计的结果。
定理4.6 若假设2.1~2.5成立,且
,则,
其中
是有限常数,具体形式在证明中给出。
证明 注意到由
的定义,
(31)
首先求(31)右式第一项的上界。由过程
和
的定义,有
两边平方取期望,由于被积元素非负,因此
(32)
下面求
的上界。对
,由(11)~(13)及假设2.4,得到
由文献 [15] 引理B.4,得到
,其中
。故利用
,得到
应用Grönwall不等式,注意
,对
,得到
(33)
其中
。结合(32)和(33),且由
,得到
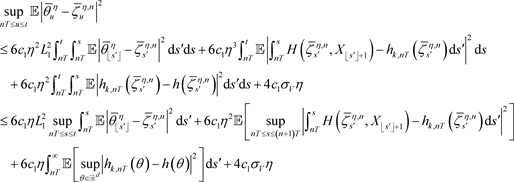 (34)
(34)
首先,求(34)右式第一项的上界。由于被积项非负,故
(35)
然后,求(34)中第二项的上界。对任意
,引入
可测事件:
(36)
对
,定义两个辅助随机过程:
由引理3.3,对任意固定的
,随机过程
满足
因此,由引理3.4,我们可以将
可测随机过程
插入随机过程
中,即得到随机过程
满足
对任意
,
,定义随机过程:
记
,显然对
有
。下面估计定理3.2中的量
,
。注意到,
(37)
故由Minkowski不等式和(8),得到
(38)
且将(37)代入(8),易得
(39)
应用定理3.2,取
,则
,且由(36)、(38)和(39),得到
(40)
由文献 [15] 引理3.3,有
故对(40)两边取期望,结合Minkowski不等式,得到
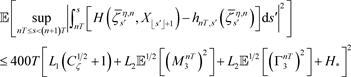 (41)
(41)
最后,求(34)中的第三项的上界。由引理4.5得到
(42)
由(34)、(35)、(41)和(42),且
,最终得到
(43)
其中
再次应用Grönwall不等式,且由
,得到
(44)
故
(45)
其中
。注意到,
且
,故
。
下面求(31)右式第二项的上界。由(11)中
的定义和(13)中
的定义,有
类似地,由前面的讨论及
,得到
(46)
(46)右边关于t是递增的,故由(44)和
,得到
应用Grönwall不等式,且由
,得到
故
(47)
其中
,且
。
最后,由(31)、(45)和(47),得到
其中
,且
。
定理4.7 (文献 [7] 推论2.6) 若假设2.1~2.5成立,且欠阻尼Langevin随机微分方程
和
的分布分别开始于
和
,则,存在常数
使得
其中常数
,
分别由文献 [7] 定理2.3和推论2.6给出,
由文献 [7] 中式(2.12)定义。
定理4.8 若假设2.1~2.5成立,且
,则
其中
,具体形式在证明中给出。
证明类似文献 [15] 定理4.2的证明,由定理4.7和文献 [7] 引理5.4,得到
其中常数
由文献 [7] 定理2.3给出。
注意
初值为
,且
,因此由引理4.3,得到
故由引理4.3和定理4.6,得到
其中
进一步计算,得到
其中
,且
。
定理3.5的证明 由定理4.6、定理4.7和定理4.8及(30),有
注意到,对任意
,
,故
其中
,
。特别地,
,
。
5. 结语
本文研究了非凸优化问题中近似采样SGHMC算法的非渐进估计。SGHMC算法是随机梯度下降算法的一个变体,该算法结合了随机梯度下降算法和哈密尔顿蒙特卡罗算法的思想,一方面通过使用随机样本帮助算法逃离局部极小值从而实现算法的全局收敛,另一方面通过引入哈密尔顿动力学思想在参数空间中模拟粒子的运动从而进行高效采样。通常的研究认为样本数据是独立的,然而实际的数据往往存在相关性。本文放宽了对数据流独立性的限制,在损失函数U非凸的情形下,以耗散性条件放宽损失函数强凸的假设,分析了全局Lipschitz条件下样本数据满足条件L混合性质时SGHMC算法的迭代分布与目标分布
之间Wassertein距离的上界,得到SGHMC算法收敛到其目标分布的速度为
,这一工作将SGHMC算法的收敛结果推广到了相关数据流的情形,说明了在样本数据独立性失效的情况下SGHMC算法的收敛性仍旧成立,从而拓宽了SGHMC算法的应用场景。研究的关键思想是将时间轴划分为长度依赖于步长
的等长区间,在此之上定义合适的辅助连续时间过程,从而将证明目标进行拆解,通过比较SGHMC算法与所定义的辅助过程之间的距离,并利用一个收缩估计的结论得到辅助过程与目标分布之间的距离,从而得到SGHMC算法的迭代分布与目标分布
之间的Wasserstein距离上界,其中条件L混合的概念及其相关矩不等式的引入为算法迭代分布与辅助过程之间距离的有界性提供了保障。本文的研究拓宽SGHMC算法的应用范围限制,进一步可以在算法本身的结构上进行优化和改造,以提高算法的效率,另外还可以考虑将该算法应用于实际场景中,通过数值实验来检验算法性能。
文章引用
杨金圆,胡良剑. 关于相关数据流的随机梯度哈密尔顿蒙特卡罗算法的非渐近估计
Non-Asymptotic Estimates for Stochastic Gradient Hamiltonian Monte Carlo Algorithm with Dependent Data Streams[J]. 应用数学进展, 2024, 13(02): 569-583. https://doi.org/10.12677/AAM.2024.132055
参考文献
- 1. Raginsky, M., Rakhlin, A. and Telgarsky, M. (2017) Non-Convex Learning via Stochastic Gradient Langevin Dynamics: A Nonasymptotic Analysis. Conference on Learning Theory, 65, 1674-1703.
- 2. Hwang, C.R. (1980) Laplace’s Method Revisited: Weak Convergence of Probability Measures. The Annals of Probability, 8, 1177-1182. https://doi.org/10.1214/aop/1176994579
- 3. Chiang, T.S., Hwang, C.R. and Sheu, S.J. (1987) Diffusion for Global Optimization in . SIAM Journal on Control and Optimization, 25, 737-753. https://doi.org/10.1137/0325042
- 4. Welling, M. and Teh, Y.W. (2011) Bayesian Learning via Stochastic Gradient Langevin Dynamics. Proceedings of the 28th International Conference on Machine Learning (ICML-11), Bellevue, Washington, 28 June 2011, 681-688.
- 5. Chen, T., Fox, E. and Guestrin, C. (2014) Stochastic Gradient Hamiltonian Monte Carlo. International Conference on Machine Learning, Bejing, 22-24 June 2014, 1683-1691.
- 6. Chau, H.N. and Rasonyi, M. (2022) Stochastic Gradient Hamiltonian Monte Carlo for Non-Convex Learning. Stochastic Processes and Their Applications, 149, 341-368. https://doi.org/10.1016/j.spa.2022.04.001
- 7. Eberle, A., Guillin, A. and Zimmer, R. (2019) Couplings and Quantitative Contraction Rates for Langevin Dynamics. The Annals of Probability, 47, 1982-2010. https://doi.org/10.1214/18-AOP1299
- 8. Chau, N.H., Moulines, É., Rásonyi, M., Sabanis, S. and Zhang, Y. (2021) On Stochastic Gradient Langevin Dynamics with Dependent Data Streams: The Fully Nonconvex Case. SIAM Journal on Mathematics of Data Science, 3, 959-986.
https://doi.org/10.1137/20M1355392
- 9. Majka, M.B., Mijatović, A. and Szpruch, Ł. (2020) Nonasymptotic Bounds for Sampling Algorithms without Log-Concavity. The Annals of Applied Probability, 30, 1534-1581. https://doi.org/10.1214/19-AAP1535
- 10. Cont, R. (2001) Empirical Properties of Asset Returns: Stylized Facts and Statistical Issues. Quantitative Finance, 1, 223-226. https://doi.org/10.1080/713665670
- 11. Gao, X., Gürbüzbalaban, M. and Zhu, L. (2022) Global Convergence of Stochastic Gradient Hamiltonian Monte Carlo for Non-convex Stochastic Optimization: Nonasymptotic Performance Bounds and Momentum-Based Acceleration. Operations Research, 70, 2931-2947. https://doi.org/10.1287/opre.2021.2162
- 12. Gerencsér, L. (1989). On a Class of Mixing Processes. Stochastics: An International Journal of Probability and Stochastic Processes, 26, 165-191. https://doi.org/10.1080/17442508908833555
- 13. Chau, H.N., Kumar, C., Rásonyi, M. and Sabanis, S. (2019) On Fixed Gain Recursive Estimators with Discontinuity in the Parameters. ESAIM: Probability and Statistics, 23, 217-244. https://doi.org/10.1051/ps/2018019
- 14. Barkhagen, M., Chau, N.H., Moulines, É., Rásonyi, M., Sabanis, S. and Zhang, Y. (2021) On Stochastic Gradient Langevin Dynamics with Dependent Data Streams in the Logconcave Case. Bernoulli, 27, 1-33.
https://doi.org/10.3150/19-BEJ1187
- 15. Akyildiz, Ö.D. and Sabanis, S. (2020) Nonasymptotic Analysis of Sto-chastic Gradient Hamiltonian Monte Carlo under Local Conditions for Nonconvex Optimization.
NOTES
*通讯作者。






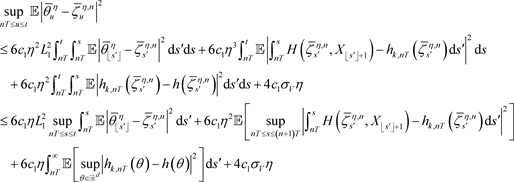 (34)
(34)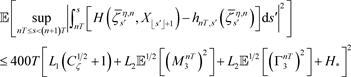 (41)
(41)