Journal of Image and Signal Processing
Vol.04 No.04(2015), Article ID:16232,7 pages
10.12677/JISP.2015.44017
Image Mosaic Technology Based on an Optimized Method of SIFT Algorithm
Cheng Yang, Xiaogang Xu, Guanlei Xu
Dalian Naval Academy, Dalian Liaoning
Email: 245591167@qq.com
Received: Oct. 6th, 2015; accepted: Oct. 21st, 2015; published: Oct. 27th, 2015
Copyright © 2015 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
In order to solve the problems of wrong feature points in the process of image mosaic algorithm based on SIFT, an optimized method is put forward. Using a new algorithm to eliminate the wrong feature points, and using the least square method to fit the new picture not only improve the matching accuracy, but also improve the image mosaic result and reduce the time of the image mosaic. Experimental results demonstrate that the method can produce high quality image mosaic.
Keywords:SIFT, Image Mosaic, The Least Square Method
基于对SIFT算法优化的图像拼接技术
杨程,徐晓刚,徐冠雷
海军大连舰艇学院,辽宁 大连
Email: 245591167@qq.com
收稿日期:2015年10月6日;录用日期:2015年10月21日;发布日期:2015年10月27日

摘 要
针对利用SIFT算法的图像拼接在匹配过程中会出现一些错误的特征点问题,提出一种对SIFT算法优化的方法。利用算法将错误的特征点除去,并且利用最小二乘法对提纯后的图像进行拟合,提高了匹配精度,对拼接效果有较好的增强,同时也缩短了拼接的时间。实验结果表明,优化后的算法可实现相对较好效果的图像拼接。
关键词 :SIFT,图像拼接,最小二乘法

1. 引言
随着计算机视觉领域的发展,图像拼接技术变成计算机图形学的一个重要的研究内容。对于不同的需要,将具有相同特征点的多幅图像拼接成一幅全景图[1] ,就能实现对需要观察的区域进行整体的实时观察。最早MORAVEC提出了基于点算子实现立体视觉匹配[2] ;之后HARRIS等人对MORAVEC算子进行了改进[3] ,但它对尺度、视角、照明变化比较敏感,而且抗噪声能力较差;LOWE提出一种更加稳定的SIFT算子[4] 。现有的拼接算法存在特征点提取不精确、拼接速度较慢等缺点。本文对SIFT算法进行了优化,先对SIFT算法匹配的特征点提纯,再用最小二乘法对提纯后的图像拟合,通过对特征点的提纯从而减少特征点的数量,同时也缩短了图像拼接的时间。
2. SIFT算法的特征匹配
2.1. 构建尺度空间
尺度空间 [5] 建立的目的是模拟图像数据的多尺度特征。由Lindeberg等人证明了高斯卷积核是实现尺度变换的唯一线性核 [6] 。对于一幅二维图像的尺度空间定义如下:

其中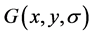 是尺度可变高斯函数。
是尺度可变高斯函数。 是图像的空间坐标,
是图像的空间坐标,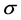 是尺度空间因子。对于不同的
是尺度空间因子。对于不同的 ,图像的平滑程度也不同,大的
,图像的平滑程度也不同,大的 值表示该图像被平滑的多,相对来说较粗糙。小的
值表示该图像被平滑的多,相对来说较粗糙。小的 值表示该图像被平滑的少,相对精细。通过建立尺度空间,构建出高斯差分尺度空间(DOG
scale-space),可以有效的获得稳定的特征点。DOG结果是通过每组上下相邻两层的高斯尺度空间图像相减得到的,如图1左部分所示。图1是由DOG算子如下:
值表示该图像被平滑的少,相对精细。通过建立尺度空间,构建出高斯差分尺度空间(DOG
scale-space),可以有效的获得稳定的特征点。DOG结果是通过每组上下相邻两层的高斯尺度空间图像相减得到的,如图1左部分所示。图1是由DOG算子如下:
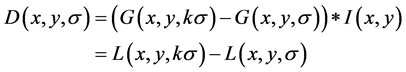
2.2. 点的搜索与定位
通过同一组内各个DOG相邻层之间的比较,完成关键点的搜索 [7] 。为了寻找尺度空间的极值点,每一个采样点要和它所有的相邻点进行比较,如图2所示,中间的检测点和它同尺度的8个相邻点和上下相邻尺度对应的9 × 2个点共26个点比较,确保在尺度空间和二维图像位置空间都检测到极值点。若待测检测点在本层已经上下两层的26个点中是最大值或最小值,则认为该点是图像在该尺度下的一个极值点。以上极值点的搜索并不是真正意义上的极值点,因为搜索是在离散空间中进行的,所以要用已知的离散空间点插值得到连续空间的极值点。运用泰勒级数展开,可以得到极值点。

Figure 1. DOG scale-space
图1. 高斯差分尺度空间

Figure 2. Detects key points in DOG scale-space
图2. 尺度空间关键点检测
泰勒展开式:
 (1)
(1)
同时对等式两变求导,求 的极值,即令
的极值,即令 ,得
,得
极值点所在的矢量位置:
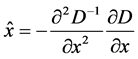 (2)
(2)
将(2)代入(1)中可以得到极值点的极值:

如果 时(假设图像的灰度值在
时(假设图像的灰度值在 之间),其响应过小,这样容易受到噪声的干扰,应丢弃。
之间),其响应过小,这样容易受到噪声的干扰,应丢弃。
2.3. 赋予特征点128维参数方向
前面确定了特征点,为每个特征点计算一个方向,利用关键点邻域像素的梯度方向分布特性为每个关键点指定方向参数,使算子具备旋转不变性 [8] 。
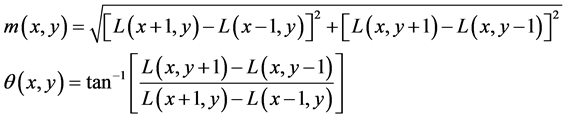
其中 为像素点梯度模值,
为像素点梯度模值,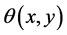 为像素点方向,
为像素点方向,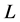 为关键点所处的尺度。
为关键点所处的尺度。
2.4. 特征描述
以关键点为中心取8 × 8的窗口,如图3。
图左中央部分为关键点,每个小格代表关键点邻域所在空间的一个像素,根据泰勒公式求出每个像素的梯度幅值与梯度方向,箭头方向代表梯度方向,箭头长度代表梯度模值,这样可以得到4 × 4 × 8 = 128维的特征向量。通过大量实验证明,128维特征向量的描述符的不变性与独特性的综合效果最优,增强了算法抗噪声的能力。
3. 利用Ransac算法进行特征点筛选
由于图像会受到噪声,光照等许多因素影响,经过上面搜索方法后得到的最近邻会存在较多的误匹配点,所以要对搜索到的点进行匹配提纯。
3.1. Ransac算法的描述
通过采样和验证的策略,求解大部分特征点都可以满足的数学模型的参数 [9] 。每次从数据集中采样模型需要的最少数目样本,计算模型的参数,然后在数据集中统计符合该模型的参数的样本数目,最多样本符合的参数就被认为是最终模型的参数值。符合模型样本的点叫做内点,不符合模型的样本点就叫做外点。在Ransac算法中,有3个参数会对其性能产生影响。这3个参数分别是:判断内外点距离阈值,估计次数和一致性集合大小阈值。
1) 内外点的距离阈值。这个阈值用来判定数据点是内点或者外点。
2) 估计次数N。令w为数据是真是数学模型内点的概率,n为确定模型参数的最少点数,如果要确定变换关系,则需要4个匹配对,即n = 4。这样,依次估计中使用的所有n个点都为内点的概率就是 。如果要保证经过N次至少有一次估计中的所有数据点都是内点的概率是p,那么N需要满足:
。如果要保证经过N次至少有一次估计中的所有数据点都是内点的概率是p,那么N需要满足:
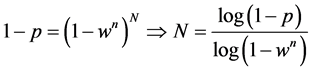
3) 一致性集合大小阈值。估计得到模型的参数后,还要统计整个数据集中符合该模型的内点数目t。令数据点是错误模型内点的概率为y,我们希望错误模型的内点数目t越小越好,即

 的值很小,一般取0.05。
的值很小,一般取0.05。
3.2. 本文的方法
通过SIFT算法对目标图片进行粗匹配,然后根据粗匹配的特征点集合,用Ransac算法将错误的特征点剔除,进而提高匹配的精度,得到第二次匹配的特征点集合。最后再用最小二乘法最大程度的拟合所有数据点,使得优化后的图像匹配的数据点最靠近真实的点,最后进行拼接。从图4中可以看出优化后的拟合线可以较好的还原真实的曲线。

Figure 3. The gradients information of key points generate eigenvector
图3. 关键点邻域梯度信息生成特征向量

Figure 4. Schematic diagram of the least square method
图4. 利用最小二乘法拟合示意
4. 实验结果
从实验结果来看,图5(c)、图5(d)两图表明在寻找特征点时,直接用SIFT算法会有一些明显错误的匹配点,而优化后的算法匹配结果较准确。图5(e)、图5(f)两图表明用SIFT算法找到特征点拼接时拼接出的图像在一定区域内存在重影,而优化后拼接的图像效果较好。表1列出的数据表明通过Ransac算法提纯后再用最小二乘法进行拟合匹配的特征点数目为102个,而直接用SIFT算法匹配找的的特征点数目是114个,优化后的算法对存在错误的特征点进行了很好的消除。拼接时间方面直接用SIFT算法拼接图像需要0.83秒,优化后的算法拼接图像需要0.79秒,时间上缩短了0.04秒,优化后的算法在图像拼接中提高了拼接的速度。
5. 结束语
本文对SIFT算法进行了的介绍,并且指出了SIFT算法的优点和缺点。针对SIFT算法的缺点引出了一种优化后的算法。通过实验表明优化后的算法不仅保存了SIFT算法的优点,而且剔除了SIFT算法在
 (a)
(a)
 (b)
(b)
 (c)
(c)
 (d)
(d) (e)
(e)
 (f)
(f)
Figure 5. (a) Mosaic image 1; (b) Mosaic image 2; (c) SIFT algorithm matching; (d) Optimized matching; (e) Mosaic results; (f) Optimized mosaic results
图5. (a) 待拼接图像1;(b) 待拼接图像2;(c) SIFT算法匹配结果;(d) 优化后匹配结果;(e) 直接拼接后的结果;(f) 优化后拼接的结果
表1. SIFT算法和优化后算法的数据对比
图像匹配时错误的特征点,使得匹配的准确性更高,图像拼接的速度更快、效果更好。今后要进一步探讨在有外界干扰的情况下图像匹配的稳定性以及匹配的精度问题,从而提高算法整体的性能。
文章引用
杨 程,徐晓刚,徐冠雷. 基于对SIFT算法优化的图像拼接技术
Image Mosaic Technology Based on an Optimized Method of SIFT Algorithm[J]. 图像与信号处理,
2015, 04(04): 139-145. http://dx.doi.org/10.12677/JISP.2015.44017
参考文献 (References)
- 1. 袁杰 (2013) 基于SIFT的图像配准与拼接技术研究. 南京理工大学, 南京.
- 2. Moravec, H.P. (1981) Rover visual obstacle avoidance. International Joint Conference on Artificial Intelligence, 3, 117-118.
- 3. Harris, C.G. and Stephens, M. (1988) A combined corner and edge detector. Proceedings of Fourth Alvey Vision Conference, 147-151.
- 4. Lowe, D.G. (2004) Distinctive image features from scale-invariant key points. International Journal of Computer Vision, 60, 91-110. http://dx.doi.org/10.1023/B:VISI.0000029664.99615.94
- 5. Perona, P., Malik, J., Perona, P., et al. (1990) Scale-space filtering and edge detection using anisotropic diffusion. IEEE Transactions on Pattern Analysis & Machine Intelligence, 12, 629-639. http://dx.doi.org/10.1109/34.56205
- 6. Lindeberg, T. (1994) Scale-space theory: A basic tool for analysing structures at different scales. Journal of Applied Statistics, 21, 224- 270.
- 7. Liao, K., Liu, G. and Hui, Y. (2013) An improvement to the SIFT descriptor for image representation and matching. Pattern Recognition Letters, 34, 1211-1220. http://dx.doi.org/10.1016/j.patrec.2013.03.021
- 8. Zhong, S., Wang, J., Yan, L., et al. (2013) A real-time embedded architecture for SIFT. Journal of Systems Architecture the Euromicro Journal, 59, 16-29. http://dx.doi.org/10.1016/j.sysarc.2012.09.002
- 9. Wu, X., Zhao, Q. and Bu, W. (2014) A SIFT-based contactless palmprint verification approach using iterative RANSAC and local palmprint descriptors. Pattern Recognition, 47, 3314-3326. http://dx.doi.org/10.1016/j.patcog.2014.04.008
