Open Journal of Transportation Technologies
Vol.
08
No.
03
(
2019
), Article ID:
30236
,
11
pages
10.12677/OJTT.2019.83027
Research on Multi-Distribution Center Vehicle Routing Optimization Method Based on Improved Multi-Layer Coding Genetic Algorithm
Lunhui Xu1, Yuchao Cao2, Baoshan Huang1
1School of Industrial Automation, Zhuhai University, Beijing Institute of Technology, Zhuhai Guangdong
2School of Civil Engineering and Transportation, South China University of Technology, Guangzhou Guangdong

Received: Apr. 29th, 2019; accepted: May 9th, 2019; published: May 16th, 2019

ABSTRACT
In order to improve logistics transportation efficiency and reduce unnecessary resource consumption, comprehensive planning of a most efficient vehicle distribution route has become a hot issue in the next logistics transportation research. There are still few studies on the situation of multiple distribution centers. The Vehicle Routing Optimization Problem (VRP) is derived from the Traveling Salesman Problem (TSP), which we classify as a non-deterministic polynomial (NP) complete combinatorial optimization problem. In the context of traffic logistics vehicle routing, this paper firstly constructs a mathematical model from the conceptual analysis of VRP problem, and then describes the theoretical basis and strategic thinking of the core algorithm—genetic algorithm to solve this problem. Finally, by adding multi-factor analysis, the comprehensive cost of evaluation is improved, and the improved multi-encoding genetic algorithm is applied to solve the multi-distribution center VRP problem, and the improvement is explored in the process.
Keywords:VRP Problem, Genetic Algorithm, Multi-Layer Coding, Transportation, Logistics, Dispatching, Path Optimization
基于改进多层编码遗传算法的多配送中心车辆路径优化方法研究
许伦辉1,曹宇超2,黄宝山1
1北京理工大学珠海学院工业自动化学院,广东 珠海
2华南理工大学土木与交通学院,广东 广州

收稿日期:2019年4月29日;录用日期:2019年5月9日;发布日期:2019年5月16日

摘 要
为了提高物流运输效率,减少不必要的资源消耗,综合规划一条最有效率的车辆配送货物的路径成为当下物流交通研究的一个热点问题。而其中多配送中心的情况研究尚少。车辆路径优化问题(VRP)是基于旅行商问题(TSP)衍生的,这类问题我们都将其归为非确定性多项式(NP)完全组合优化问题。本文在交通物流车辆路径规划的背景下,首先从VRP问题的概念分析出发,构建了一个数学模型,然后对本文解决该问题的核心算法——遗传算法的理论基础及策略思路进行了一个描述。最后通过加入多因素分析,改进了评价的综合成本,将改进多层编码的遗传算法应用于解决多配送中心VRP问题,并在过程中探索改进。
关键词 :VRP问题,遗传算法,多层编码,交通运输,物流,调度,路径优化

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
1.1. 选题背景
现代物流系统是由运输、存储、包装、配送、装卸等若干个复杂流程组成的一个完整系统 [1] 。其中车辆运输系统是物流中一个重要的直接与消费者以及供应商相连的环节,对运输车辆的路径选择进行优化调度,可以提高物流运输的经济效益、提高目标双方的整体收益,也是未来发展智能交通运输系统和开展电子商务的基础。
根据配送中心数目的多少,有单配送中心车辆调度问题和多配送中心车辆调度问题之分。在实际的城市物流体系中,往往存在多个配送中心。因此,对多配送中心车辆调度问题的研究具有重要的现实意义 [2] 。
1.2. 国内外研究现状
针对于普通的单中心VRP问题,早期的研究者们一般采用精确算法进行求解,其方法主要包括了分支定界算法,列生成算法,动态规划算法以及分支切割算法等。然而随着研究者们对问题路网范围的扩大,一般的研究方法已经无法满足现在大规模网络的需求,随之结合智能算法的方法应运而生,目前智能算法又分为两大类:1) 求解VRP的传统启发式算法:如先安排路线后分组的方法、先分组后安排路线的方法、改进–交换法、节约插入法、基于数学规划的算法和交互式优化算法等 [2] [3] [4] 。2) 求解VRP的现代启发式算法:诸如人工神经网络、遗传算法、模拟退火算法、禁忌算法等 [5] 。就目前的情况而言,VRP算法研究中的大多数学者都致力于上述智能算法的研究。
现有对配送车辆调度问题的研究主要集中在单配送中心问题上,对多配送中心车辆调度问题的研究很少,国内对该问题的研究基本上是空白。国外的Renaud, De saulniers, Wu, Kazaz, Sumichrast, Irnick等专家对多配送中心车辆调度问题进行了研究 [6] [7] ,并取得了一些有价值的研究成果。
本文在现有研究成果的基础上,建立了多配送中心车辆调度问题的数学模型,并且综合考虑总代价值,以综合代价为依据,将多配送中心车辆调度问题分解为多个单配送中心车辆调度问题进行求解的策略,利用智能算法中的遗传算法,设计了求解多配送中心车辆调度问题的算法,最后通过实验计算验证了该算法的良好性能。
2. 车辆调度优化问题分析
2.1. 多配送中心车辆调度问题的数学模型
多配送中心车辆调度问题可以描述为:从多个供应商用多台车辆向多个需求商送货。其中,供应商以及需求上的位置坐标是固定的,配送运输的车辆所能装载的货物量也是一个最优值的情况下。并且其他配置能够满足运输需求,问题的本质就是要求合理安排车辆配送路线,使目标函数得到优化 [8] [9] ,其中目标函数的定义由各自需求决定,并满足以下条件:
①每条配送路径上各需求商的需求量之和不超过车辆的载重量;
②每条配送路径的长度不超过车辆一次配送的最大行驶距离;
③每个需求商的需求必须满足,且只能由一台车辆送货。
设某城市中有H个供应商,要给M个需求商送货,每个供应商服务的需求商构成一个配送分区.设第h个供应商要向 个需求商送货,第h个供应商有 台配送车辆,每台车辆的载重量为纵 ,其一次配送的最大行驶距离为 。第h个供应商服务的第i个需求商的货物需求量为 ,需求商i到j的运距为 ,该供应商到第j个需求商的距离为 ,再设 为第h个供应商中第k台车辆配送的需求商数( 表示未使用第k台车辆),用集合 表示第h个区域中的第k条路径,其中的第i个元素 表示需求商 在第h个区域中的路径k中的顺序为i (不包括供应商),令 表示配送中心,若以配送总时间最短为目标函数,则可建立如下多配送中心车辆调度问题的数学模型:
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
上述模型中,(1)式为目标函数,即要求配送总时间(即各条配送路径的时间之和)最短;(2)式保证每条路径上各客户的货物需求量之和不超过车辆的载重量;(3)式保证每条配送路径的长度不超过车辆一次配送的最大行驶距离;(4)式表明某配送分区每条路径上的客户数不超过该分区的总客户数;(5)式表明某配送分区各条配送路径上的客户数之和等于该分区的总客户数;(6)式表明每个客户都得到配送服务;(7)式表示每条路径的客户的组成;(8)式限制每个客户仅能由一台车辆送货;(9)式表示当区域h中第k辆车服务的客户数 ≥ 1时,说明该台车参加了配送,则取 ,当第k辆车服务的客户数 < 1时,表示未使用该台车辆,因此取 。
2.2. 遗传算法
遗传算法(Genetic Algorithm, GA)是通过模拟生物进化过程来完成优化搜索的,由美国J. Holland教授提出的一类借鉴生物界自然选择和自然遗传机制的随机化搜索算法。其主要特点是群体搜索策略和群体中个体之间的信息交换,搜索不以梯度信息为基础。它尤其适用于处理传统搜索方法难于解决的复杂和非线性问题作为一种全局优化搜索算法 [5] [10] 。针对本论文的车辆路径问题有很好的适用性。
3. 车辆调度优化问题的建模
3.1. 遗传算法解决问题的基本思想
本文根据著名学者Goldberg总结出的一个最基本的遗传算法流程,我们将它称为基本遗传算法(Simple Genetic Algorithms, SGA)。 [11] 的思路为出发点,构建如图1所示的思路流程。
基于遗传算法解决问题的核心思想,体现在“优胜劣汰”这一自然规律的生物进化过程 [12] ,这一优化过程的目标是对环境的适应性(fitness),而生物种群通过生物体的遗传、变异来达到优化(亦即进化)之目的,应用于交通领域解决本文的VRP问题中,简单来说即背景条件为,物流配送公司数量为n,要将重量为m的货物配送到x个目标点,最后返回出发点。同时对运输的条件进行限制约束(如时间范围约束、车辆容量限制、车辆行驶里程数、某次出行最大工作时间等),达到一定的目标(如车辆行驶路程最短、运输费用最少、使用车辆数最少,服务质量最高等)。

Figure 1. SGA flow diagram
图1. SGA流程图
3.2. VRP问题的影响因素分析
本文的一大创新点在于,除了时间因素外,考虑到多配送中心车辆调度问题的目标函数中,还存在其他众多影响路径决策的影响因素,因此本文应用层次分析法综合考虑了其他会影响物流运输效益的因素,优化模型中的目标函数 [13] [14] 。后建在应用遗传算法得到综合的最优路径规划。
一、成本类影响因素
根据《中国物流年鉴》(2011)的数据,成本类影响因素是供应商进行运输时需要考虑的一个重要因素 [10] ,2010的运输成本占社会物流总成本的53.99%,占企业总物流成本的50%以上。因此影响成本的因素是物流运输路径选择模型中必须考虑的重要因素。它主要包括如下:
1) 运输距离;2) 运输环节;3) 运输相关的运营成本;4) 货物数量
二、服务类影响因素
在如今的物流市场竞争中,虽然仍由效率等因素占主导地位,但与服务相关的服务质量,服务态度等社会因为也渐渐成为客户选择的参考点之一,因此不仅仅成本作为VRP问题的一个目标,本文将服务类影响也作为一个评价标准进行讨论,包括如下:
1) 与时间相关的因素:a) 货物的运到期限,b) 货物的在途时间;2) 与交货质量相关的因素;3) 线路状态;4) 信息化管理水平。
3.3. 影响因素的确定以及评价标准
根据上述的影响因素,本文采用层次分析法进行影响因素比重的确定。层次分析法(Analytic Hierarchy Process,简称AHP)是对一些较为复杂、较为模糊,难以定量得出的问题做出决策的简易方法,它是由美国运筹学家T. L. Saaty于上世纪70年代初期提出的一种简便、灵活而又实用的多准则决策方法 [15] 。
运用层次分析法建模,大体上可按下面四个步骤进行,并且通过图2表示相应的流程图:

Figure 2. Hierarchical analysis flow diagram
图2. 层次分析流程图
1) 建立递阶层次结构模型;
2) 构造出各层次中的所有判断矩阵;
3) 层次单排序及一致性检验;
4) 层次总排序及一致性检验。
根据如表1所示的重要度对照表,按照本文各因素的影响程度得出如表2所示的比较矩阵。
Table 1. Analytic hierarchy importance reference table
表1. 层次分析重要度对照表
Table 2. Hierarchical analysis importance table
表2. 层次分析重要度值表
根据上述比较矩阵,通过matlab运算得出各影响因素权重。
weight vector: 0.37721 0.1619 0.28694 0.082043 0.024833 0.025908 0.015824 0.025346
CI = 按照各比例重要度,以及影响水平,本文选取运输距离,货物数量(重量),货物的在途时间,线路状态(对道路的破坏水平)四个指标进行影响因子的构建:
进行归一化处理
(10)
得到 。
4. 多层编码遗传算法解决VRP问题的实现
遗传算法本身有较强的问题求解能力,能够解决非线性优化问题。对于简单的问题来说,染色体可以方便地表达问题的潜在解,然而,对于较为复杂的优化问题,一个染色体难以准确的表达问题的解 [16] 。本文在传统遗传编码的基础上,结合车辆调度的实际情况,应用多层编码遗传算法,把个体分为多层,定义每层编码均表示不同的含义,通过多层编码完整表达了问题的多项参数,以及最终的解。多层编码遗传算法扩展了遗传算法的使用领域,使得遗传算法可以方便用于复杂问题求解 [11] [17] [18] [19] 。
4.1. 模型构建
车辆路径问题是根据供应商和需求商相互之间的供求关系,从而达到合理利用资源,提高经济效益的目的。在多层编码中,车辆路径可以描述为m个供应商要配送物品到n个需求点,其中运输批次的不同表示每批次运输的货物种类的等有区别,该数学模型可以描述为
1) 供应集 ,mj表示第j个需求点, 。
2) 需求集 ,mj表示第i个供应点, 。
3) 路径序列集 , ,表示供应商车辆所运送对应物资opi的运输批次。
4) 可提供相关所需物资的供应商的集合表示为
其中 ,表示物资opi的运输批次j可选择的供应商。
5) 时间矩阵T, ,表示第i个供应商pi第j批次到达目的地的时间。
6) 代价矩阵C, ,表示第i个供应商pi第j批次到到达目的地的各方面代价总和。
4.2. 算法实现
1) 个体编码
采用整数排列编码方法。每个染色体表示全部供应商的运输顺序,当需求点的总数量为n,送达需求商ni所需物资的供应商为mj时,则个体表示长度为 的整数串。其中,染色体的前半部分表示需求商在选择供应商编号的运输序列,后半部分表示每次运输的对应的供应商的序号。如个体:
[2 4 3 1 1 2 3 4 2 1 3 3 2 2 1 3]
该个体表达了4个运输序列都是2次,由3个供应商配送的运输顺序,其中,前8位表示车辆的运输顺序,为需求商2 → 需求商4 → 需求商3 → 需求商1 → 需求商1 → 需求商2 → 需求商3 → 需求商4;9到16为表示所提供对应物资的供应商点,依次为供应商2 → 供应商1 → 供应商3 → 供应商3 → 供应商2 → 供应商2 → 供应商1 → 供应商3。
2) 适应度值
设染色体的适应度值为全部供应完成时间,适应度值计算公式为
 (11)
(11)
其中,time指全部任务完成时间,全部任务完成时间越短,该染色体越好。
3) 选择操作
选择操作采用轮盘赌法选择适应度较好的染色体,个体选择概率为
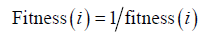 (12)
(12)
其中,pi(i)表示染色体i在每次选择中被选择的概率。
4) 交叉操作
种群通过交叉操作获得心染色体,从而推动整个种群向前进化,交叉操作首先从种群中随机选取两个染色体,并取出每个染色体的前 位,然后随机选择交叉位置进行交叉。
如:
个体-
极值-
5) 变异操作
种群通过变异操作获得新的个体,从而推动整个种群向前进化。变异算子首先从种群中随机选取变异个体,然后选择变异位置pos1和pos2,最后把个体中pos1和pos2位的运输序列以及对应的需求点序号对换,如交叉位置为2和4时:
个体-
6) 计算交叉以及编译操作后适应度(即时间代价)值。
4.3. 算例
4.3.1. 配送案例
构建某地区,有6个需求商,根据需求需要6种不同的物资。供应商的数量为10个,能提供的车辆数为10辆(每个供应商对应1辆车)。分别按照一定要求为6个需求点送货。假设每个供应商的车辆均符合统一标准,即车辆载重能满足运输需求;车辆的最大行驶距离能够满足一次完整的OD行程。根据实际需求,每个供应商所提供的物资运到不同所需需求商的路径代价不同,本文路径代价的计算,就基于上一章对各影响因素的层次分析所得出的不同权重比,其中本文算例的供需对应关系随机生成,运输距离随机生成,货物数量(重量)随机生成,货物的在途时间只考虑与运输距离的线性关系,线路状态假设为同等条件,应用式(10),进行综合计算。每个供应商可提供的需求商需求物资如表3所示。具体的路径代价向权图如表4所示。两个表是结合对应的,如可以把物资运到需求商1的供应商选择为3号车辆运送时,最终的代价函数为3,选择10号供应商的车辆运送的代价为5。目标需求就是规划出一次整体代价最小的路径系统。
供应商不同批次的供应需求表如下。
Table 3. Supply and demand materials supply and demand correspondence table
表3. 供需商物资供需对应表
Table 4. Transport final cost list
表4. 运输最终代价表
结合点到点之间一对一的影响因素综合分析,应用层次分析法综合得到评价矩阵系数如下:例供应商3号车辆运送原料1给需求商1,其路径长度为30 km,载重量10 kg,运输时间3小时,道路破损顿规定为1。
计算后的最终代价为15。
4.3.2. 配送方案验证
通过matlab软件,应用所提出的算法对某一案例进行仿真验证。
试验结果得出完成该地这次运输任务的最短评价标准,以及最优调度方案图如图4所示。同时在最大迭代次数为50的条件下,通过多层编码遗传算法需要迭代10次得到最优结果,有一个较好的收敛结果,如图3所示。
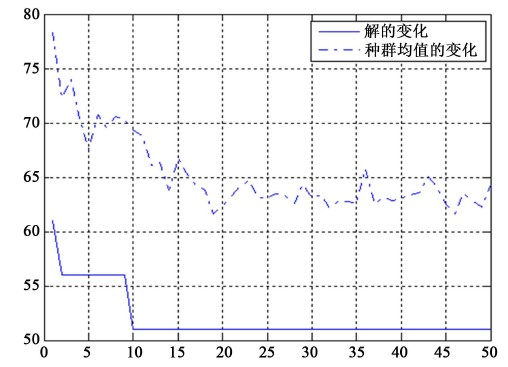
Figure 3. Iteration number map
图3. 迭代次数图
基于多层编码遗传算法得到的左右规划调度图如图4所示,其中纵坐标表示供应商编号车辆;横坐标表示代价。例如供应商1号车辆中,601表示把第1种物资运送到6号需求商。横坐标对应于改长度的绝对值是该次运输的代价。

Figure 4. Vehicle dispatch map
图4. 车辆调度图
针对于本案例中小型规模的实际运输问题,我们以一个最直观的角度去计算。即优先选择代价表中的最小值进行配送,如优先选在1号车辆,为需求商4运输物资原料6;5号车辆为需求上6运输物资原料3。通过直观的认为判断,最终得出的总体代价值(315)要大于本论文所提出的方法得到的最终结果(260)。对于更大规模的该类问题,往往也无法通过直观的判断得出结论。而本文中可以通过改变改进遗传算法的种群规模M和迭代次数GEN来适应不同规模的问题,验证改进算法同时具有一个优于传统算法的收敛精度和速度。
5. 结论
本论文主要从当下车辆调度的热门多中心问题出发,对于如何规划一个全局最优路径,结合在该问题上有良好表现的遗传算法,进行了如下研究:
1) 对于物流运输中多配送中心,构建了相应数学模型进行描述。
2) 应用改进的多层编码遗传算法加入多影响因子构建了一个解决多配送中心的车辆调度及路径规划问题的方法。
3) 通过实际案例需求,构建了可视化表格进行问题描述,应用所研究的方法,证实可以得到一个完整的全局代价最小的路径规划网络。
多配送中心车辆调度问题是一类非常重要的组合优化问题在现实生活中的体现,曾经的研究多集中于单个配送中心问题。传统的遗传算法存在一些缺点:染色体单一,局部搜索能力差,容易出现早熟,收敛速度慢。通过案例实验证明,利用本文的改进的多层遗传算法解决的多配送中心车辆调度问题,能够得到较好的全局搜索结果,并且有一个较快的收敛速度效果。
本文所进行的研究,离真正的实际应用还有一定的差距。例如本文所做的研究是把评价标准以自己的方式定义,并不是一个公认的定义方法,以及其他影响因素由于调查来源等的局限性,不能完全保证符合所有实际预期。
文章引用
许伦辉,曹宇超,黄宝山. 基于改进多层编码遗传算法的多配送中心车辆路径优化方法研究
Research on Multi-Distribution Center Vehicle Routing Optimization Method Based on Improved Multi-Layer Coding Genetic Algorithm[J]. 交通技术, 2019, 08(03): 222-232. https://doi.org/10.12677/OJTT.2019.83027
参考文献
- 1. 薛戈丽, 王建平. 一种基于蚁群算法的物流配送VRP解决方案[J]. 计算机系统应用, 2012, 21(2): 200-203.
- 2. 崔雪丽, 马良, 范炳全. 车辆路径问题(VRP)的蚂蚁搜索算法[J]. 系统工程学报, 2004, 19(4): 418-422.
- 3. 李向阳. 遗传算法求解VRP问题[J]. 计算机工程与设计, 2004, 25(2): 271-273+276.
- 4. 方金城, 张岐山. 物流配送车辆路径问题(VRP)算法综述[J]. 沈阳工程学院学报(自然科学版), 2006, 2(4): 357-360.
- 5. 钟石泉. 物流配送车辆路径优化方法研究[D]: [博士学位论文]. 天津: 天津大学, 2007.
- 6. Wazirali, R.A., Alzughaibi, A.D. and Chaczko, Z. (2014) Adaptation of Evolutionary Algorithms for Decision Making on Building Construction Engineering (TSP Problem). International Journal of Electronics and Telecommunications, 60, 113-116. https://doi.org/10.2478/eletel-2014-0015
- 7. Ma, H., Yang, Z., You, P. and Fei, M. (2017) Multi-Objective Biogeography-Based Optimization for Dynamic Economic Emission Load Dispatch Considering Plug-in Electric Vehicles Charging. Energy, 135, 101-111. https://doi.org/10.1016/j.energy.2017.06.102
- 8. 贾楠, 吕永波, 付蓬勃, 等. 物流配送问题中VRP的数学模型及其求解算法[J]. 物流技术, 2007, 26(4): 54-56.
- 9. 彭其华. 一种车辆路径优化调度算法的研究与仿真[J]. 计算机仿真, 2014, 31(5): 143-146.
- 10. 周生伟, 蒋同海, 张荣辉. 改进遗传算法求解VRP问题[J]. 计算机仿真,2013, 30(12): 140-143+157.
- 11. 宗辰光, 于培培, 费利鹏, 等. 基于多层编码粒子群——遗传算法融合的AGV调度问题研究[J]. 机电工程技术, 2016, 45(4): 11-14.
- 12. 胡飞虎, 马贝龙, 杨丽, 等. 基于改进遗传算法的应急物资配送车辆调度优化问题研究[J]. 计算机应用研究, 2014, 31(10): 2928-2932+2936.
- 13. 石彪, 池宏, 祁明亮, 等. 应急物资运输的两阶段车辆调度模型[J]. 系统工程, 2012, 30(7): 105-111.
- 14. 饶卫振. 大规模动态车辆路径问题优化方法研究[M]. 北京: 经济科学出版社, 2018.
- 15. 孔祥丽. 多影响因素下的导航路网数据路径规划研究[D]: [硕士学位论文]. 武汉: 武汉大学, 2018.
- 16. 郎茂祥. 多配送中心车辆调度问题的模型与算法研究[J]. 交通运输系统工程与信息, 2006, 6(5): 65-69.
- 17. 王保中, 康立山, 何巍. 基于实数编码遗传算法的多层神经网络BP算法[J]. 武汉大学学报(自然科学版), 1998, 44(3): 26-28.
- 18. 谢思聪, 陈小波. 基于多层编码遗传算法的两阶段装配式建筑预制构件生产调度优化[J]. 工程管理学报, 2018, 32(1): 18-22.
- 19. 王琛, 游伟, 袁泉, 等. 一种基于多层编码遗传算法的虚拟网络功能调度方法[J]. 信息工程大学学报, 2018, 19(3): 275-281.
