Nuclear Science and Technology
Vol.05 No.03(2017), Article ID:21513,7
pages
10.12677/NST.2017.53022
Mathematical Model of Hydrogen Isotope Separation Column in Circulating Cooling Condition
Xiangbo li, Shilin Hu, Yi Kang, Hailin Bai
China Institute of Atomic Energy, Beijing

Received: Jul. 10th, 2017; accepted: Jul. 23rd, 2017; published: Jul. 26th, 2017

ABSTRACT
Based on the classic Newton’s law of cooling and combined with the mathematical methods such as differential equation, iterative method, least square method and linear fitting analysis, a new mathematical model is established. The mathematical model can be used to analyze the cooling curve of hydrogen isotope separation column which was cooled by both natural ventilation cooling and circulating cooling, predict the required cooling time and guide the selection of cooling conditions.
Keywords:Cooling Mathematical Model, Newton’s Law of Cooling, Iterative Method
氢同位素分离柱的循环冷却数学模型
李祥波,胡石林,康艺,白海林
中国原子能科学研究院,特种材料工程部,北京
收稿日期:2017年7月10日;录用日期:2017年7月23日;发布日期:2017年7月26日

摘 要
本文基于经典的牛顿冷却定律,采用微分方程、迭代法以及最小二乘法线性拟合分析等数学方法,建立了新的数学模型。该数学模型可以较好地分析自然冷却和循环冷却两种条件同时作用于氢同位素分离柱时的冷却曲线,预测冷却所需要的时间,进而指导冷却条件的选择。
关键词 :冷却数学模型,牛顿冷却定律,迭代法

Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
氢同位素分离柱的冷却是置换色谱法分离氢同位素中的重要环节。在热解吸置换色谱分离氢同位素中,当需要进行连续分离时,已经完全释放出氢的分离柱需要进行快速冷却,以备下一批次的原料气的进入;在热循环吸附分离法分离氢同位素的过程中,每个分离柱都要不断重复加热-冷却的过程,自动控制的方式使得其对冷却速率等条件的要求更为严格 [1] [2] 。
为保证分离柱的设计能够满足使用要求,目前的研究方向主要集中在通过冷却实验测定指导设计分离柱结构,而关于此方面的理论研究则较少。通过设计数学模型找出分离柱冷却的规律,计算出所需要的冷却时间,可指导分离柱的设计及使用,减少实验工作量,同时更加有利于分离过程的自动化控制。
在冷却系统中,为了在短时间内将分离柱冷却至较低温度,除了靠分离柱的自然散热冷却外,通常还会对分离柱进行循环气冷或循环水冷。由于同时存在自然冷却和循环冷却两种作用,无法通过简单计算得到分离柱从一个温度冷却到另一温度所需要的时间。本研究基于经典的牛顿冷却定律,通过微分方程、迭代法以及最小二乘法线性拟合分析等数学方法,建立了新的数学模型,较好地解释了自然冷却和循环冷却同时作用于氢同位素分离柱的冷却规律。
2. 实验装置
实验所用的所有设备如表1所示。
实验装置及流程如图1所示:冷却气由缓冲罐中经气体循环泵抽出,进入热交换器中冷却后,进入分离柱的下端,再由分离柱上端离开,最后回到缓冲罐中,完成一次循环冷却。
为了保证实验误差,整个实验装置置于恒温、通风良好的环境中;实验过程中所用冷却气的压力和流量固定不变;热交换器的冷却水温度恒定,以保证冷却气的温度的稳定。
3. 自然冷却条件下的冷却模型
当分离柱温度高于室温时,即开始与环境中的空气进行热交换,本文称之为分离柱的自然冷却。只要分离柱温度高于室温,即使无其他任何冷却手段,由于自然冷却的存在,其温度也会逐渐下降。因此,研究分离柱的冷却模型,首先要研究分离柱的自然冷却规律。
热量的交换主要有热传导、热对流和热辐射三种形式 [3] 。理论上物体冷却时,这三种热交换形式都可能存在。对于分离柱的自然冷却,由于分离柱并无与气体良导热体直接接触,因此热传导可以忽略,其自然冷却主要依靠热对流和热辐射。又由于分离柱处于通风良好的环境中,因此热对流为分离柱自然冷却的主要形式。而热对流这种冷却作用,通常遵循物理学中经典的牛顿冷却定律。
牛顿冷却定律是传热学基本定律之一,是温度高于周围环境的物体向周围媒质传递热量逐渐冷却时所遵循的规律 [4] 。当物体表面与周围存在温度差时,单位时间从单位面积散失的热量与温度差成正比,
Table 1. Experimental instruments
表1. 实验仪器
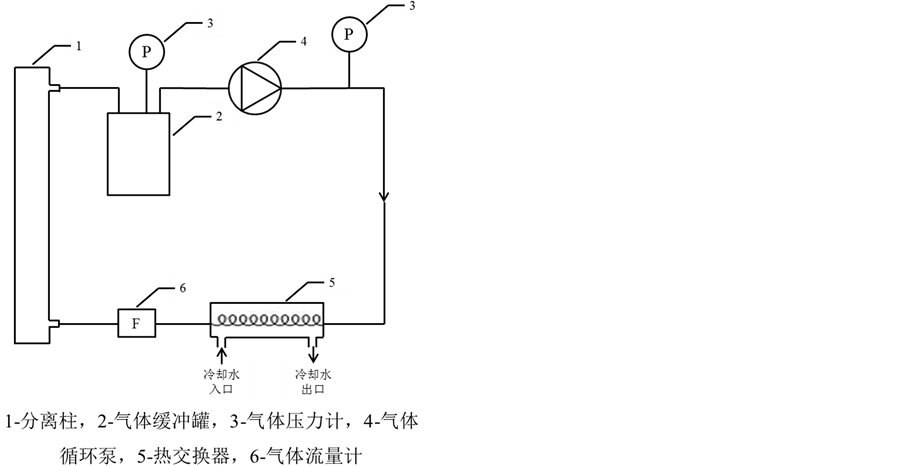
Figure 1. Flowchart of circulating cooling simulation experiment
图1. 循环冷却模拟实验流程图
比例系数称为热传递系数(本文称之为冷却系数)。
根据牛顿冷却定律,分离柱的降温速率与物体与环境的温度差成正比,即
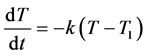
其中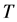 为分离柱当前温度,
为分离柱当前温度, 为环境温度,
为环境温度, 为与温度无关的常数。上式积分可得:
为与温度无关的常数。上式积分可得:

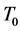 为分离柱初始温度。以
为分离柱初始温度。以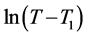 对
对 作线性拟合,即可求出冷却系数
作线性拟合,即可求出冷却系数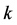 。
。
为验证牛顿冷却定律对该装置的适用性,本研究中将分离柱加热至300℃。该温度下保持30 min后,停止加热,使分离柱自然冷却,记录不同时间分离柱上三个测温点的温度,取其平均值作为分离柱的温度 。结果如图2、图3所示:其中图2为该条件下分离柱温度
。结果如图2、图3所示:其中图2为该条件下分离柱温度 随时间
随时间 变化曲线,图3为
变化曲线,图3为 对
对 的线性拟合结果。
的线性拟合结果。
由图2可知,随着分离柱温度的降低,降温速度也逐渐降低,降温呈现为先快后慢的过程。
由图3可知,以牛顿冷却模型作为分离柱自然冷却的数学模型,拟合的线性方程R = 0.99953,线性拟合结果较好,说明牛顿冷却定律符合分离柱冷却的实际情况,因此可以用该定律来处理分离柱的冷却问题。

Figure 2. Temperature curve of separating column under natural cooling conditions
图2. 自然冷却条件下分离柱的温度曲线

Figure 3. Linear fitting results under natural cooling conditions
图3. 自然冷却条件下的线性拟合结果
通过牛顿冷却定律,拟合得到分离柱的自然冷却系数k = 0.00835 min−1。该系数不随分离柱的温度变化而变化,因此当有其它冷却形式作用于分离柱时并不影响自然冷却系数的值。因此对于同一根分离柱,可以认为其自然冷却系数为常数。
4. 循环冷却条件作用下的冷却模型
实际生产过程中分离柱除了自然冷却,同时还要在夹层中通入冷却气进行循环冷却,则牛顿冷却定律不再适用,因此我们需要建立新的数学模型来处理自然冷却与循环冷却同时作用于分离柱时冷却系数的计算。
设冷却气温度为 ,分两种情况讨论:
,分两种情况讨论:
(1) 冷却气温度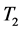 = 环境温度
= 环境温度 。
。
两种冷却作用都应符合牛顿冷却定律。设自然冷却系数为 ,循环冷却系数为
,循环冷却系数为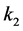 ,则总的冷却效果应为两种冷却效果之和,即
,则总的冷却效果应为两种冷却效果之和,即




以 对
对 作线性拟合,其斜率即为
作线性拟合,其斜率即为 。由此可知,若冷却气温度等于室温,则总的冷却系数
。由此可知,若冷却气温度等于室温,则总的冷却系数 ,即二者简单加和可得。由于自然冷却系数
,即二者简单加和可得。由于自然冷却系数 可事先由牛顿冷却模型求得,且并不因循环冷却的存在而改变,因此可求得循环冷却系数
可事先由牛顿冷却模型求得,且并不因循环冷却的存在而改变,因此可求得循环冷却系数 。
。
(2) 冷却气温度
 环境温度
环境温度 。
。
类似的,其冷却的微分方程为:
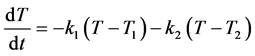

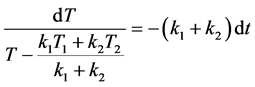
积分可得
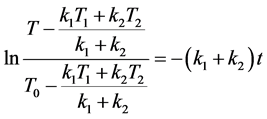
即

因为 为常数,因此有
为常数,因此有

由于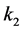 未知,常规数学方法无法线性拟合出斜率
未知,常规数学方法无法线性拟合出斜率 ,因此我们尝试用迭代法求出
,因此我们尝试用迭代法求出 的数值 [5] 。先假设
的数值 [5] 。先假设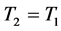 ,则有
,则有

以 对
对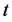 作一次线性拟合,其斜率为
作一次线性拟合,其斜率为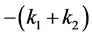 ,进而求出
,进而求出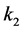 。将求出的
。将求出的 代入
代入 ,并以
,并以 对
对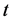 作二次线性拟合,则可得到一个新的斜率值
作二次线性拟合,则可得到一个新的斜率值 ,进而求出一个新的
,进而求出一个新的 值。将得到的新
值。将得到的新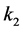 继续代入公式中拟合,直到代入的
继续代入公式中拟合,直到代入的 值与拟合得到的
值与拟合得到的 值相等,最终求得的
值相等,最终求得的 即为真实值。
即为真实值。
为验证这一模型,同样的,将分离柱置加热至300℃。该温度下保持30 min后,停止加热,同时开启气体循环泵循环冷却分离柱(冷却气流量恒定,流量v = 24.8 L·min−1),记录不同时间三个测温点的温度,取其平均值作为分离柱的温度 。图4为该条件下分离柱温度 随时间 变化图,图5为
。图4为该条件下分离柱温度 随时间 变化图,图5为 对
对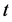 的一次线性拟合结果。
的一次线性拟合结果。
由一次拟合结果可得 。将
。将 代入
代入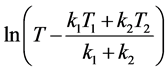 ,并以
,并以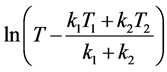 对
对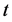 继续作线性拟合,每次拟合出的结果如表1所示。
继续作线性拟合,每次拟合出的结果如表1所示。
由表2可知,在保留至小数点后第五位的精度下,迭代法进行到第四次拟合时,得到的结果与第三次相同,说明该精度下拟合结果已接近真实值。第四次拟合结果如图6所示。

Figure 4. Temperature curve of separating column under circulating cooling conditions
图4. 循环冷却条件下分离柱的温度曲线

Figure 5. First linear fitting results under circulating cooling conditions
图5. 循环冷却条件下的一次线性拟合结果

Figure 6. Fourth linear fitting results under circulating cooling conditions
图6. 循环冷却条件下的第四次拟合结果
Table 2. Results of each linear fitting
表2. 线性拟合结果
求得的总冷却系数k = 0.01530 min−1,循环冷却系数k2 = 0.00695 min−1。根据最终拟合的结果,R = 0.99829,线性拟合程度较好。因此,该模型较好地处理和预测两种冷却作用下的温度变化问题。
5. 总结
通过理论计算和实验验证,本文采用

来处理分离柱的循环冷却问题。先通过简单的自然冷却实验求出自然冷却系数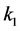 ,再以
,再以 对
对 作多次线性拟合,采用迭代法求出
作多次线性拟合,采用迭代法求出 的数值。实验证明,根据该模型,可以较好地预测分离柱从一个温度冷却至另一温度所需的时间。采用该数学模型计算得到的数据,线性拟合程度较好,也说明该模型能较好地反映两种冷却条件同时作用时的真实规律。
的数值。实验证明,根据该模型,可以较好地预测分离柱从一个温度冷却至另一温度所需的时间。采用该数学模型计算得到的数据,线性拟合程度较好,也说明该模型能较好地反映两种冷却条件同时作用时的真实规律。
文章引用
李祥波,胡石林,康艺,白海林. 氢同位素分离柱的循环冷却数学模型
Mathematical Model of Hydrogen Isotope Separation Column in Circulating Cooling Condition[J]. 核科学与技术, 2017, 05(03): 170-176. http://dx.doi.org/10.12677/NST.2017.53022
参考文献 (References)
- 1. 蒋国强, 罗德礼, 陆光达, 孙灵霞. 氚和氚的工程技术[M]. 北京: 国防工业出版社, 2007.
- 2. 彭述明, 王和义. 氚化学与工艺学[M]. 北京: 国防工业出版社, 2015.
- 3. 霍尔曼J.P., 等. 传热学[M]. 北京: 人民教育出版社, 1979.
- 4. 过增元. 热流体学[M]. 北京: 清华大学出版社, 1992.
- 5. 菲赫金哥尔茨. 微积分学教程[M]. 北京: 高等教育出版社, 2006.
