N体问题复合区域解析函数近似计算 Numeric Model of N-Body Problem on Domains

doi:10.12677/CSA.2013.31001

设为首页加入收藏期刊导航网站地图

期刊菜单

文章导航

Computer Science and Application 计算机科学与应用, 2013, 3, 1-5

http://dx.doi.org/10.12677/csa.2013.31001 Published Online February 2013 (http://www.hanspub.org/journal/csa.html)

Numeric Model of N-Body Problem on Domains*

Chao Liu, Shesheng Zhang#

School of Science, Wuhan University of Technology, Wuhan

Email: #sheshengz@qq.com

Received: Oct. 31st, 2012; revised: Nov. 27th, 2012; accepted: Dec. 8th, 2012

Abstract: In this paper, proximately compute interacted N-body problem by analytic function, Analytic expression of

radial distribution function of particles interacting is denoted by multiple integral, the analysis solution is obtained on

double sphere domains. In the case of M = 1800, the error of analytic solution is less than 0.001, and numeric CPU time

is much less than direct computation. The two polypeptide chains protein radial function is obtained, and points out that

this method needs to be improved.

Keywords: Particle Simulation; N-Body Problem; Radial Distribution Function; Multiple Integral

N体问题复合区域解析函数近似计算*

刘超，章社生#

武汉理工大学理学院，武汉

Email: #sheshengz@qq.com

收稿日期：2012 年10 月31日；修回日期：2012 年11月27 日；录用日期：2012年12月8日

摘要：研究粒子模拟的计算问题，推导出单连通区域和复连通区域的粒子相互作用径向分布函数的解析解，

得到了双球域的分析解，对计算复杂性进行了研究，结果表明，当粒子数 M = 1800 时，计算误差小于千分之一，

分析解的计算时间非常少。对蛋白质的距离函数计算结果表明，分析解能显著减少计算量。

关键词：粒子模拟；N体问题；径向分布函数；多重积分

1. 引言

在粒子模拟数据分析中，双体关联函数查询–空

间距离直方图(SDH)的研究[1,2]极其重要。文献[3 ]介绍

了Barnes2Hut 算法(BHA)和快速多极子方法(FMM)，

认为都是基于树结构的快速算法。BHA 可快速计算各

点受到的场力，计算复杂度为，但计算精

度通常只有1%；FMM 通过层次划分和位势函数的多

极子展开计算各点位势，其复杂度为 O(N)，却能达到

任意精度。SDH 也是描述系统的一系列的重要物理量

的主要建筑模块，是一种被称为径向分布函数(RDF)[4]



logON N

的连续统计分布函数的直接估计。因此，RDF 可看成

是连续化的 SDH。RDF 对计算物理系统热力学特征

是不可或缺的[5]，直接与该系统的结构因子(structure

factor) 相关联[6]。在实际应用中，为简化计算，RDF

通常是以 SDH 这样一种非连续的形式出现。文献[7]

讨论了 N体问题解析函数近似计算，用多重积分表示

粒子相互作用径向分布函数的解析表达式，求出了圆

盘区域和球体区域相互距离分析解。文献[7]的工作表

明，用解析表达式计算径向函数，能显著减少计算量

和计算误差。



文献[7]中的结论是基于假设粒子分布是稠密的。

但在实际中，存在粒子分布是多区域的情况，如原子

在具有多链的蛋白质中的分布[8]，其分布在多个区域，

*基金项目：国家自然科学基金资助项目(No. 51139005)。

#通讯作者。

N体问题复合区域解析函数近似计算

若用文献[7]中的方法计算，将会产生较大误差。本文

将在文献[7]的工作基础上，建立多区域的N体问题解

析函数近似计算模型，用多重积分表示粒子相互作用

径向分布函数的解析表达式。

2. 多区域基本计算原理

在文献[7]中，径向分布函数(RDF)的定义为









 (2.1)

式中



是在粒子之间距离为r，厚度为 h的球壳内

粒子距离数量，称为距离和函数，分母为分子所有取

值的和。设粒子坐标为 Xi，，则距离和函

数

1, ,iN

r可表示为：













 rr (2.2)

这里 *

rXX为Xi与Xj之间的距离，函数 δh =

1(当* 2rrh 时)，函数δh = 0(当* 2rrh 时)。

根据空间距离直方图(SDH)的定义[2]。为了消去重复累

加，式中除以 2。用一个立方体 Ω包含所有粒子。按

粒子分布的稀疏情况，将立方体Ω划分为 N'个子区域

Ωk，。则距离和函数

1, ,k

N



r可表示为：



1, 1



F

(2.3)

式中 ,ij

为第 i个区域中的粒子与第 j个区域中的粒子

之间的距离和函数。当j = i 时，表示第i个区域内部

粒子之间的距离和函数。当j ≠ i时，表示第i个区域

中的粒子与第j个区域中的粒子之间的距离和函数。

距离和函数



r也可写为：



'''

1,1, 1

NNN

hii

iiji

rF F







下面用高维重积分近似方法计算粒子之间的距离和

函数。

3. 单区域内距离和函数

当N' = 1 时，距离和函数为一个单区域，用一个

立方体 Ω包含单区域内所有粒子，再将立方体划分为

M个边长为 H的小立方体 dΩ，第i个小立方体 dΩi

内的粒子数为n(i)，小立方体的中点坐标为 Yi，第i

个小立方体中点和第j个小立方体中点的距离为



，用









nin j YY



近似表示两个小立方体内

所有粒子之间的距离的和。将下标i, j从1取到 M，

然后求和，则有





r的近似计算式：

 





rninjr









 (3.1)

式中 *

rYY



，设 dV 为小立方体的体积，记





ini dV



，则上式为：



/2 *

MM h

hjih

rdVdVrr

 







r

式中 δ为delta 函数。根据多维积分的定义，上式可写

为

 

 



Fr Frr

rXXXrr















 X

(3.2)

上式是 N个粒子径向分布函数的近似积分表达式，其

积分区域为立方体区域Ω的乘积 Ω*Ω，密度







取

对应小立方体的







值。上式还可化为下面形

式：







 

 



FrXf XrX

XrXrrX















 (3.3)

这里





Xr是以 X为圆心，r为半径的球面与区域 Ω

相交部分密度积分值。



r是径向连续分布函数。

当区域 Ω为圆盘和球体，密度为均匀分布时，可以得

到解析表达式。

3.1. 圆盘解

设密度为均匀分布ρ，区域Ω为半径R的圆盘，

当0 < r ≤ R时，用上面公式求得积分值：

 

π4πd

rrRRr rqq













 (3.4)

当R < r ≤ 2R时，

 

π4πd

rrRrRrqq













 (3.5)

3.2. 球域解

考虑密度为均匀分布 ρ，区域 Ω为半径 R的球域。

用上面计算公式，当0 < r ≤ R时，可求得

N体问题复合区域解析函数近似计算

 



π2

FrrrR rRrR

rRR rRr

























类似地，当 R < r ≤ 2R时，有







24 223

π233

Fr r

rRrRrRrRR





















(3.6)

4. 双区域径向分布

我们考虑粒子分布在两个区域A和B，区域内分

别有 N和N'个粒子，对应粒子密度分别为 ρ和ρ'(粒

子数除区域的体积)，则粒子距离和函数可以表示为

 





11 1222h



rFrFrFr (4.1)

式中 r = mh，h为步长， 1, 2, 3,m



。





为区域

A内部粒子产生的距离和函数，



r为区域B内部

粒子产生的距离和函数，





r为区域球A中的粒与

区域 B的粒子相互作用产生的距离和函数。若 A, B区

域为球域，则有区域内函数表达式，即



r和





用上节中的公式计算：



1411

2326

102

kkk kkkkk k

kk kk

kk k

Fr b

rRr R

Frr R



 















(4.2)

式中 k = 1, 2，且，以及，

252



h1

RR2





。

下面推导





r的计算公式。

设点 Y为球 B表面点，坐标为 Y，它到点 A的距

离为 L，则点Y与球 A中粒子距离和函数为：





hhj

YrXY r













(4.3)

根据空间距离直方图(SDH)的定义[2]，将球域 A划分

为M'个子区域 dΩ，第 i个子区域dΩi内的粒子数为

n(i)，子区域的中点坐标为Xi，第 i个子区域中点和区

域外点 Y的距离为 i

Y，用



ni XY近似表示

第i个子区域内所有粒子与在 Y点粒子的距离的和。

将下标 i从1取到M'，然后求和，则有的近似

计算式：



 



hhi

YrniX Y r















(4.4)

设dV 为子区域的体积，记



ini dV



，应用δ函数，

上式可写为：



YrXY rrV











i

根据多维积分的定义，当 dV 非常小时，上式可近似

写为

 





/2 d

Yr Yrr

YrXrXYX











 (4.5)

这里





Yr为点 Y与球A中的粒子距离为 r的个数，

称为点 Y到球 A的距离密度函数。当粒子密度ρ和ρ'

都为常数时，由点与球的几何关系，经过积分运算，

有解析计算式：

 

πr

YrRL r

LRr LR















(4.6)

当rLR



或rLR



时，。上式只与距离

L和R有关，与粒子坐标Y无关。容易求得，球心在

A点，半径为L的球与球 B的相交面积为



0Yr



πL

SR'aLaR'La

 R'



 



上面两式相乘，计算得球B内与球A的球心距离为L

的全部粒子与球A中的粒子的距离密度函数为：

  

222

gLr'RLrR'a L





 





 

(4.7)

上式对 L从L1到L2积分，计算得两球距离中粒子相

互距离为 r的距离密度函数：













122 1

rGLrGLr

(4.8)

式中

 



 



332 5

GLr'RR'LLa

raR'Lr

rLaLr











 













且有 L1和L2取值计算式

rR rRaR

LaR rRaR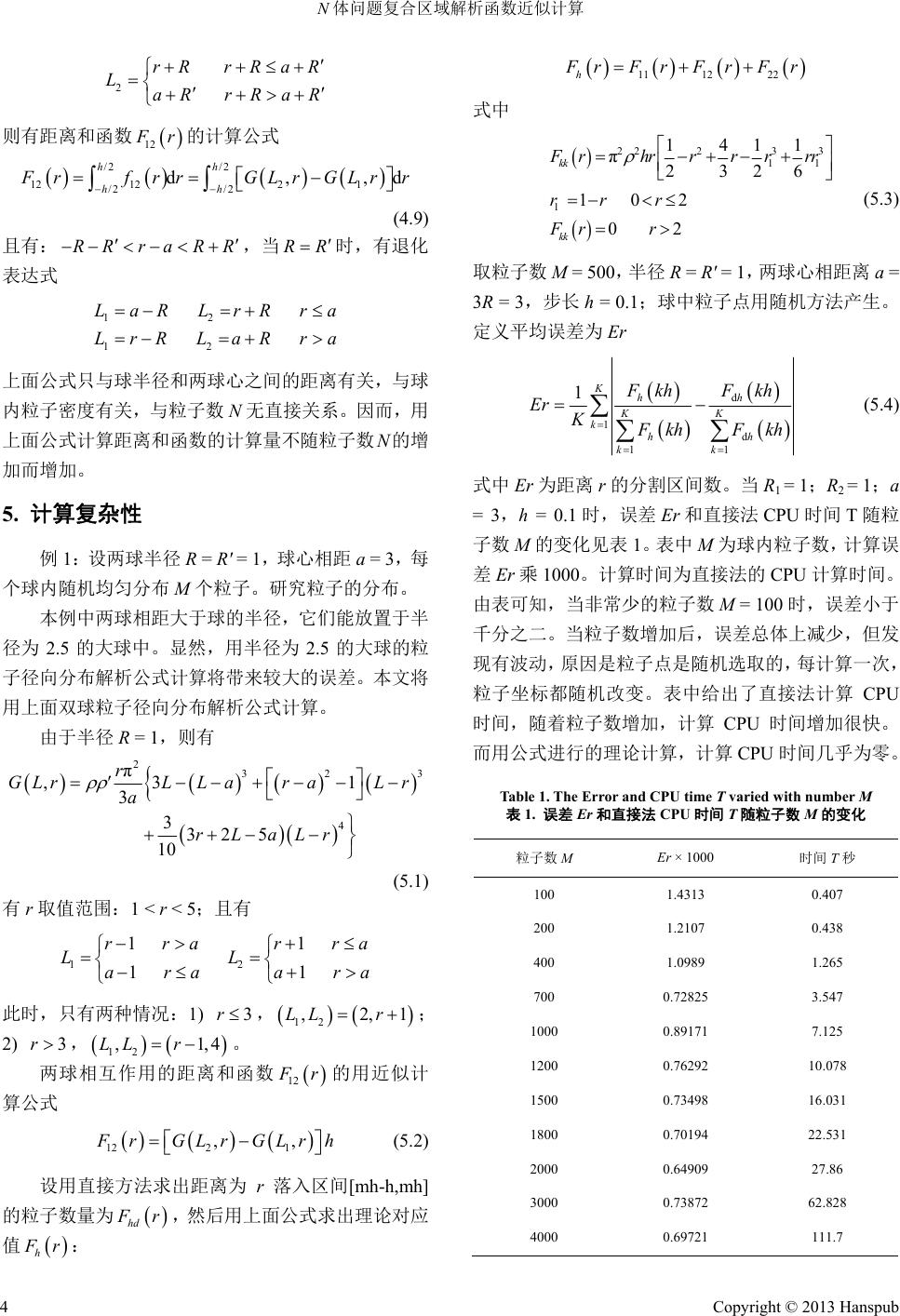



















N体问题复合区域解析函数近似计算

rR rRaR

LaR rRaR













则有距离和函数





r的计算公式

 

/2 /2

12122 1

/2 /2

hh ,d

rfrrGLrGLr



 r











(4.9)

且有：，当时，有退化

表达式

RRra RR



  





LaRLrRra

LrR LaR ra

 

 

上面公式只与球半径和两球心之间的距离有关，与球

内粒子密度有关，与粒子数 N无直接关系。因而，用

上面公式计算距离和函数的计算量不随粒子数 N的增

加而增加。

5. 计算复杂性

例1：设两球半径R = R' = 1，球心相距 a = 3，每

个球内随机均匀分布M个粒子。研究粒子的分布。

本例中两球相距大于球的半径，它们能放置于半

径为 2.5 的大球中。显然，用半径为2.5 的大球的粒

子径向分布解析公式计算将带来较大的误差。本文将

用上面双球粒子径向分布解析公式计算。

由于半径 R = 1，则有

 







232

,3 1

3325

GLr'LL ar aL r

rLaLr



















(5.1)

有r取值范围：1 < r < 5；且有

rra rr

ara ar

 







 



此时，只有两种情况：1) 3r



，；

2) ，。



,2,LL r



3r



,1LL r



两球相互作用的距离和函数





r的用近似计

算公式



122 1

rGLrGLr





h (5.2)

设用直接方法求出距离为 r落入区间[mh-h,mh]

的粒子数量为



r，然后用上面公式求出理论对应

值





r：









11 1222h



rFrFrFr

式中



2223 3

1411

π2326

102

Frhrrrrrr

rrr

Fr r

















 



(5.3)

取粒子数 M = 500，半径R = R' = 1，两球心相距离 a =

3R = 3，步长h = 0.1；球中粒子点用随机方法产生。

定义平均误差为Er



1Khh

khF kh

Er K

khF kh









(5.4)

式中 Er 为距离r的分割区间数。当R1 = 1；R2 = 1；a

= 3，h = 0.1时，误差 Er 和直接法CPU 时间 T随粒

子数 M的变化见表1。表中 M为球内粒子数，计算误

差Er 乘1000。计算时间为直接法的 CPU 计算时间。

由表可知，当非常少的粒子数M = 100 时，误差小于

千分之二。当粒子数增加后，误差总体上减少，但发

现有波动，原因是粒子点是随机选取的，每计算一次，

粒子坐标都随机改变。表中给出了直接法计算 CPU

时间，随着粒子数增加，计算CPU 时间增加很快。

而用公式进行的理论计算，计算CPU 时间几乎为零。

Table 1. The Error and CPU time T varied with number M

表1. 误差 Er 和直接法 CPU 时间 T随粒子数 M的变化

粒子数 M Er × 1000 时间T秒

100 1.4313 0.407

200 1.2107 0.438

400 1.0989 1.265

700 0.72825 3.547

1000 0.89171 7.125

1200 0.76292 10.078

1500 0.73498 16.031

1800 0.70194 22.531

2000 0.64909 27.86

3000 0.73872 62.828

4000 0.69721 111.7

N体问题复合区域解析函数近似计算

6. 生物中的应用

径向函数在蛋白质设计中有重要的地位，快速计

算径向函数能显著提高设计速度[8]。应用上面理论，

我们对蛋白质原子间距离径向分布进行计算，选取蛋

白质 1B2M，在蛋白质数据库 PDB 中下载文件

1B2M.pdb，去掉与蛋白质无关的数据，保留二条蛋白

质肽链，它的第一个肽链有 781 个原子，全部原子质

心在点 A(13.239,17.966, 3.696)，坐标用原子单位，下

面有关数据都使用原子单位。第二个链有 782 个原子，

全部原子质心在点B(1.9036, 39.84, 19.184)，两质心相

距29.05 原子单位。以质心 A和B作半径为R = 14.5

的球，分别包含有两个603 个原子和 605个原子。作

为本文理论在蛋白质中的初步应用，本例不计算球外

粒子对径向函数的贡献，不考虑原子质量，只将原子

当成一个粒子。原子数除体积，得近似粒子密度分别

为0.04722 和0.047376 ，用前面理论进行了径向和函

数计算，并与直接法计算结果进行了比较，结果表明，

计算误差为千分之 0.9839，直接法计算 CPU 时间这

2.703 秒，理论计算CPU时间几乎为零。计算结果表

明，随着半径 R的增大，球内原子数增加，计算误差

减少，直接法计算CPU 时间增加。

7. 结束语

分析解能显著减少距离函数的计算量，提高计算

精度。本文根据子模拟的计算问题，推导出单连通区

域和复连通区域的粒子相互作用径向分布函数的解

析解，得到了双球域的分析解，对计算复杂性进行了

研究，结果表明，当%粒子数 M = 1800 时，计算误差

小于千分之一，分析解的计算时间非常少。对蛋白质

的距离函数计算结果表明，分析解能显著减少计算

量。

参考文献 (References)

[1] 胡旻, 祝大军, 刘大刚, 周俊, 刘盛纲. 粒子模拟软件吸收边

界的研究[J]. 强激光与粒子束, 2006, 18(8): 1315-1318.

[2] Y.-C. Tu, S. P. Chen and S. Pandit. Computing distance histo-

grams efficiently in scientific databases. Proceedings of ICDE,

Shanghai, 29 March-2 April 2009: 796-807．

[3] 王武, 冯仰德, 迟学斌. 树结构在N体问题中的应用[J]. 计算

应用研究, 2008, l25(1): 42-44.

[4] M. Bamdad, S. Alavi B. Najafi and E. Keshavarzi. A new ex-

pression for radial distribution function and infinite shear modulus

of Lennard-Jones fluids. Chemical Physics, 2006, 325(2-3): 554-

562．

[5] 陈念贻, 徐驰, 李通化. LiF-KCl熔盐溶液的 Monte Carlo法计

算机模拟研究——I. 径向分布函数和热力学性质[J]. 中国科

学(B 辑), 1987, 1: 21-26．

[6] A. Filipponi. The radial distribution function probed by X-ray

absorption spectroscopy. Journal of Physics: Condensed Matter,

1994, 6(41): 8415-8427.

[7] 陈绍平, 章社生. N体问题解析函数近似计算[J]. 数值计算与

计算机应用, 2011, 2: 143-147.

[8] F. Eshel, Y. Yang, S. S. Zhang and Y. Q. Zhou. Predicting con-

tinuous local structure and the effect of its substitution for sec-

ondary structure in fragment-free protein structure prediction.

Structure, 2009, 17(11): 1515-1527.