Advances in Education
Vol.4 No.04(2014), Article ID:13873,4 pages
DOI:10.12677/AE.2014.44011
The Function of Counterexamples in the Teaching of Real Variable Function
College of Mathematics, Physics and Information Engineering, Jiaxing University, Jiaxing
Email: tangjohn@126.com
Copyright © 2014 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received: May 1st, 2014; revised: May 22nd, 2014; accepted: Jun. 1st, 2014
ABSTRACT
Using counterexamples appropriately in real variable function can not only make the students understand the definition and grasp the theorem and proposition, but also correct students’ errors, stimulate their interest in discussing and raise their thought ability.
Keywords:Real Variable Function, Counterexamples

反例在实变函数教学中的作用
汤约翰
嘉兴学院数理与信息工程学院,嘉兴
Email: tangjohn@126.com
收稿日期:2014年5月1日;修回日期:2014年5月22日;录用日期:2014年6月1日

摘 要
在实变函数教学中,恰当地运用反例,不仅能使学生准确地理解定义、正确掌握定理和命题,还能纠正学生的错误认识,激发学生探讨问题的兴趣,培养学生的思维能力。
关键词
实变函数,反例

1. 引言
实变函数是数学专业重要的通识基础课。通过学习实变函数,可以培养学生严密的逻辑思维能力和数学的思想方法,运用点集分析方法分析问题和解决问题的能力,为学习有关专业课程和扩大数学知识方面提供必要的数学基础[1] [2] 。而要学好实变函数,首要的问题是要让学生掌握实变函数中的基本概念和基本性质[3] 。根据我们的经验,在实际教学中解决这个问题的一个有效方法是恰当地使用反例。在数学中,要确立一个命题为真,必须在已有的知识之上,经过一系列的逻辑推理予以证明,而要说明一个命题为不真,只需举一个与命题结论不符的例子就够了。这种用来说明某个命题为不真的例子,通常称为反例(counterexamples [4] )。
2. 实变函数中反例的常见类型
2.1. 一些简单命题的反例
例1:任意多个开集之交集未必为开集。
【反例】设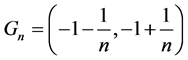 ,
,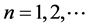 ,每个
,每个 为开集,但
为开集,但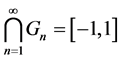 不是开集。
不是开集。
例2:若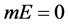 ,则
,则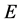 未必是可数集。
未必是可数集。
【反例】设 是Cantor集,则
是Cantor集,则 ,但
,但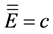 ,故
,故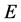 为不可数集。
为不可数集。
2.2. 改变命题条件得到的反例
实变函数中有许多数学命题,其条件有多个,当条件发生改变(增加、减少或变换)时,导致命题不真的反例就是改变命题条件得到的反例。
例1:【命题】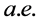 收敛的函数列必依测度收敛。
收敛的函数列必依测度收敛。
【分析】命题错误。因为Lebesgue定理要求必须有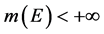 这个条件。
这个条件。
【反例】取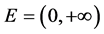 ,作函数列:
,作函数列:
显然 ,当
,当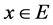 。但当
。但当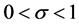 时,
时,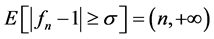 ,且
,且 这说明
这说明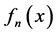 不测度收敛到1。
不测度收敛到1。
例2:【命题】对于任意可测集合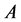 ,
,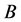 ,如果
,如果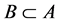 则有
则有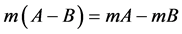 。
。
【分析】命题错误。如果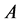 ,
,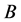 都是测度无限集合,显然结果不成立。
都是测度无限集合,显然结果不成立。
【反例】任何测度无限集合的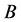 都可作为反例。
都可作为反例。
2.3. 逆命题的反例
例1:【命题】若 是可测函数,则
是可测函数,则 必是可测函数。
必是可测函数。
【逆命题】若 是可测函数,则
是可测函数,则 必是可测函数。
必是可测函数。
【反例】设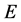 是
是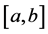 上的不可测集,
上的不可测集,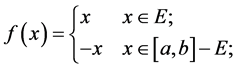
则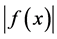 是
是 上的可测函数,但
上的可测函数,但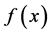 不是
不是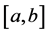 上的可测函数。
上的可测函数。
例2:【命题】如果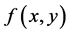 Lebesgue可积,则
Lebesgue可积,则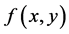 的两个累次积分存在且相等。
的两个累次积分存在且相等。
【逆命题】如果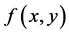 的两个累次积分存在且相等,则
的两个累次积分存在且相等,则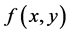 Lebesgue可积。
Lebesgue可积。
【反例】设
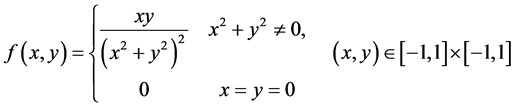 则虽然
则虽然 的两个累次积分存在且相等,但
的两个累次积分存在且相等,但 Lebesgue不可积。
Lebesgue不可积。
3. 反例在实变函数教学中的作用
3.1. 有助于让学生准确理解基本定义
通过运用反例,常常能从反面消除一些容易出现的模糊认识,有助于让学生严格区分那些相近的、易混的概念,抓住概念的要素和本质,从而达到较好的教学效果。
例如:集合的基数的定义比较抽象,通过举反例可以加深学生对此概念的理解。如有的学生观察到有限集合不能与其真子集合具有相同的基数,就据此得出任何集合不能与其真子集具有相同基数的结论。此时,我们给出整数集合和它的真子集自然数集合的基数相同的反例。通过这个反例不仅加深了学生对集合基数的理解,而且也让学生看到了有限与无限的本质区别。
3.2. 有助于让学生正确掌握基本定理和命题
在实变函数的定理和命题教学中,运用生动的反例驳斥错误是非常有效的。反例可以用来说明真命题的适用范围,这对于初学者是非常有帮助的,不仅能澄清一些错误的认识,对基本定理和命题作出正确的理解,也能促使学生形成严密推理和重视条件的习惯。
例如: 收敛的函数列未必几乎一致收敛。
收敛的函数列未必几乎一致收敛。
取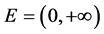 ,作函数列:
,作函数列:
显然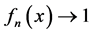 ,当
,当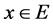 。
。
另一方面:

这个反例让学生对叶果洛夫定理的条件“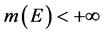 ”的重要性有了清醒的认识。
”的重要性有了清醒的认识。
3.3. 有助于纠正学生错误的认识,激发学生探讨问题的兴趣
举反例和证明是数学的两大重要思维方式。学生在实变函数学习中的创造性,常常离不开直觉思维,但因为直觉思维不够严谨,所以仅凭直觉所得的猜想可能伴有错误。此时,教师引导学生在学习的过程中发现反例,就可以纠正猜想中可能带来的错误。
学生在某一学习阶段,因为受过去认知的习惯性影响,对当前事物的认知容易产生思维定势。教师可根据学生的心理特点,抓住机会恰当地运用反例,消除学生的思维定势,激发学生探讨问题的兴趣。
例如:学生受Lebesgue积分可看作是Riemann积分的推广的影响,总认为Lebesgue积分也能看作是非正常Riemann积分的推广,但事实上可举反例来否定。
例如: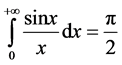 ,但是相应的
,但是相应的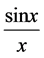 在
在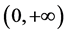 上却不是Lebesgue可积分的。
上却不是Lebesgue可积分的。
3.4. 有助于培养学生的思维能力
3.4.1. 有助于培养学生思维的严密性
例如:命题测度有限集上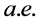 有限的非负可测函数Lebesgue可积。该命题不成立。一般只能说积分
有限的非负可测函数Lebesgue可积。该命题不成立。一般只能说积分
确定,只有当积分有限时才叫做可积。可以举反例: 在
在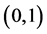 上却不是Lebesgue可积的。通过这样引
上却不是Lebesgue可积的。通过这样引
导学生举反例,就有助于培养学生思维的严密性。
3.4.2. 有助于培养学生思维的发散性
实变函数教学中可经常选择一些需要较强发散性思维的典型问题,通过创设问题情景,引导学生构造反例,鼓励学生勇于并善于发现问题、提出问题,鼓励并支持学生富有创造性因素的思维活动,从而培养学生思维的发散性。
例如:刚刚上面的反例除了可以举 在
在 上,还有没有其它的反例呢?通过分析我们知道任何有
上,还有没有其它的反例呢?通过分析我们知道任何有
限集上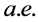 有限的非负无界可测函数都满足要求。显然这样的反例有无穷多个。
有限的非负无界可测函数都满足要求。显然这样的反例有无穷多个。
3.4.3. 有助于培养学生思维的深刻性
例如:由于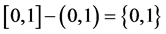 ,故有学生就认为不存在使
,故有学生就认为不存在使 和
和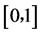 之间
之间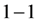 对应的映射。我们记
对应的映射。我们记 中有理数全体
中有理数全体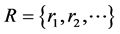 ,
,
令
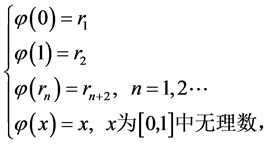
则显然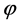 是
是 到
到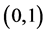 上的
上的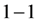 映射。通过这样引导学生举反例,就有助于培养学生思维的深刻性。
映射。通过这样引导学生举反例,就有助于培养学生思维的深刻性。
3.4.4. 有助于培养学生思维的灵活性
反例在剖析错误上具有直观性强、说服力强等显著特点,重视反例教学不仅能使学生发现错误,而且还可以完善相关知识,学会从多个角度思考问题,从而培养学生思维的灵活性。
例如:有学生认为连续函数一定是有界变差函数。可以举反例: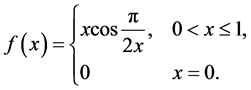
显然是 上的连续函数。如果对
上的连续函数。如果对 取分划
取分划 ,则容易证明
,则容易证明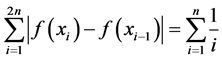 ,从而得到
,从而得到 。
。
基金项目
嘉兴学院教改项目(85151325),国家自然科学基金项目(11301225)。
参考文献 (References)
- [1] 程其襄等 (2010) 实变函数与泛函分析基础(第三版). 高等教育出版社, 北京.
- [2] 胡适耕 (1999) 实变函数. 高等教育出版社, 北京.
- [3] 周民强 (1985) 实变函数. 北京大学出版社, 北京.
- [4] Rudin, W. (1974) Real and Complex Analysis. McGraw-Hill, New York.