Pure Mathematics
Vol.4 No.04(2014), Article ID:13775,6 pages
DOI:10.12677/pm.2014.44015
Notes for the Generalization of the Matrix’s Rank Equalities
School of Mathematics and Statistics, Hainan Normal University, Haikou
Email: linsy1111@aliyun.com, 959041689@qq.com
Copyright © 2014 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received: May 12th, 2014; revised: Jun. 10th, 2014; accepted: Jun. 16th, 2014
ABSTRACT
In this paper, by using the block matrixes and their elementary transformation, we generalize the rank equalities of a class of matrix.
Keywords:Block Matrix, Elementary Transformation, Similar Matrixes

关于推广型矩阵秩等式的注记
林诗游,陈人珍
海南师范大学数学与统计学院,海口
Email: linsy1111@aliyun.com, 959041689@qq.com
收稿日期:2014年5月12日;修回日期:2014年6月10日;录用日期:2014年6月16日

摘 要
在本文中,我们运用分块矩阵及其初等变换将一类矩阵秩的等式进行再推广。
关键词
分块矩阵,初等变换,相似矩阵,等价

1. 引言
分块矩阵是线性代数中的重要内容,在线性代数中具有重要的地位。分块矩阵的初等变换是处理矩阵问题的一种重要方法,在运算中,把这些小矩阵当作数一样处理,从而把一个高阶矩阵分成若干个低阶矩阵来运算,再运用其初等变换做进一步的处理,常常能达到迅速解决问题的目的。分块矩阵的初等变换在线性代数中有广泛的应用,尤其是在计算矩阵的秩时,能提高解题的速度,减少一些不必要的计算。以下两个结论见于文献[1] :
结论1:设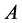 为
为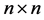 矩阵且
矩阵且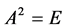 ,则秩
,则秩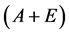 +秩
+秩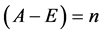 。
。
结论2:设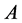 为
为 矩阵且
矩阵且 ,则秩
,则秩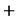
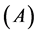 秩
秩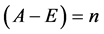 。
。
文献[2] 已经将这两个结论作了推广,即
结论3:设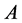 为
为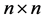 矩阵且
矩阵且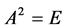 ,则秩
,则秩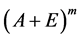 +秩
+秩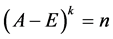 ,其中
,其中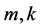 是任意自然数。
是任意自然数。
结论4:设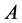 为
为 矩阵且
矩阵且 ,则秩
,则秩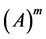 +秩
+秩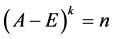 ,其中
,其中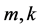 是任意自然数。
是任意自然数。
问题的提出:当对条件进行进一步的推广时,是否也有类似的结论?
问题一:当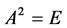 时,有秩
时,有秩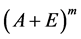 +秩
+秩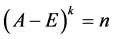 这个结论,若把
这个结论,若把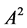 推广到
推广到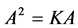 或
或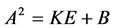 会不会也有类似的结论呢?如果有,
会不会也有类似的结论呢?如果有, 中的
中的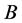 应该满足什么条件?
应该满足什么条件?
问题二:前面已经证明了条件在实数域上结论成立,那么,如果把条件推广至复数域会不会也成立呢?
本文的主要内容是利用分块矩阵的初等变换将一类矩阵秩的等式进行再推广。我们首先列举出相关的性质和定义,参见文献[1] -[7] :
定义1 矩阵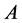 与
与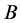 成为等价的,如果
成为等价的,如果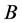 可以由
可以由 经过一系列初等变换得到。
经过一系列初等变换得到。
定义2 相似矩阵:设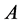 ,
, 为
为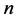 阶矩阵,如果有
阶矩阵,如果有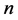 阶可逆矩阵
阶可逆矩阵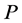 存在,使得
存在,使得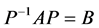 成立,则称矩阵
成立,则称矩阵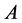 与
与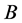 相似,记为
相似,记为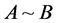 。
。
定义3 由单位矩阵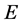 经过一次初等变换得到的矩阵称为初等矩阵。
经过一次初等变换得到的矩阵称为初等矩阵。
设 是一个
是一个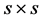 分块单位阵:
分块单位阵: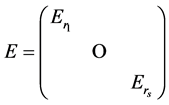 ,其中
,其中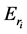 是一个
是一个 阶单位阵
阶单位阵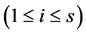 。
。
定义4 分块单位阵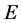 经过一次初等变换所得到的分块阵称为分块初等阵。
经过一次初等变换所得到的分块阵称为分块初等阵。
分块初等阵有三种,它们分别对应着三种初等变换:
1) 对换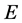 的第
的第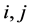 两行(列)所得的分块初等阵记为
两行(列)所得的分块初等阵记为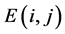 ;
;
2) 用可逆阵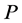 左(右)乘
左(右)乘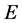 的第
的第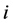 行(列)所得的分块初等阵记为
行(列)所得的分块初等阵记为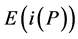 ;
;
3) 用矩阵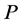 左乘
左乘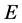 的第
的第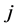 行再加到第
行再加到第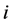 行所得到的分块初等阵记为
行所得到的分块初等阵记为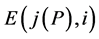 ,它同时也表示用
,它同时也表示用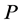 右乘
右乘 的第
的第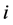 列再加到
列再加到 列所得的分块初等阵。
列所得的分块初等阵。
设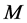 是由
是由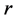 行
行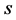 列子矩阵
列子矩阵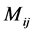 所构成的
所构成的 分块矩阵:
分块矩阵: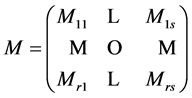 ,其中
,其中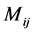 是一个
是一个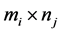 矩阵。
矩阵。
定义5 初等变换:分块矩阵的行变换和列变换称为分块矩阵的初等变换。
分块矩阵的下列三种变换称为初等行(列)变换:
1) 对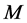 进行行(列)对换;(用
进行行(列)对换;(用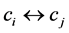 表示对换
表示对换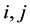 两行(列));
两行(列));
2) 用一个可逆阵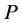 左(右)乘
左(右)乘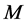 的某一行(列)的所有子矩阵;
的某一行(列)的所有子矩阵;
3) 分块矩阵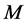 的某一行(列)的所有子矩阵左(右)乘一个矩阵
的某一行(列)的所有子矩阵左(右)乘一个矩阵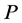 再加到另一行(列)的对应子矩阵上。
再加到另一行(列)的对应子矩阵上。
性质1 对分块矩阵进行一次初等矩阵行(列)变换,相当于对原矩阵进行一系列初等行(列)变换。
性质2 分块初等变换不改变分块阵的秩,如果分块矩阵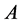 经过有限次分块矩阵的初等变换化为
经过有限次分块矩阵的初等变换化为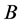 ,则
,则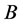 的秩等于
的秩等于 的秩。
的秩。
性质3 每一类分块矩阵的初等变换都是有限次普通初等变换的连续叠加。
性质4 设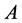 是一个
是一个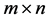 分块矩阵,对
分块矩阵,对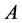 施行一次初等行变换相当于在
施行一次初等行变换相当于在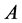 的左边乘以相应的
的左边乘以相应的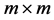 分块初等阵;对
分块初等阵;对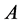 施行一次初等列变换,相当于在
施行一次初等列变换,相当于在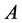 的右边乘以相应的
的右边乘以相应的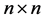 分块初等阵。
分块初等阵。
下面将在前人的基础上对这类矩阵秩的等式进行再推广。
2. 主要结果及其证明
为得出即将证明的定理,我们首先给出相关引理及其证明过程:
引理 1设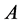 为数域
为数域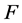 上的一个
上的一个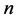 阶方阵,且满足
阶方阵,且满足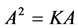 。则
。则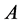 与对角矩阵
与对角矩阵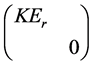 相似,其中
相似,其中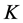 为任意给定的实数。
为任意给定的实数。
证:由 ,所以
,所以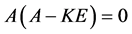 ,设
,设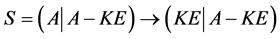 ,由性质2知秩
,由性质2知秩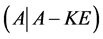 = 秩
= 秩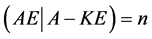 。因此在
。因此在 中存在
中存在 阶子式
阶子式 ,即矩阵
,即矩阵 可逆,设
可逆,设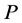 的前
的前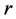 列所组成的子块
列所组成的子块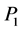 在
在 中,后
中,后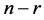 列所组成的子块
列所组成的子块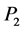 在
在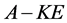 中,即
中,即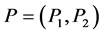 ,
, ,
,
由于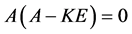 ,知
,知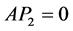 ,所以
,所以
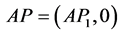 (1)
(1)
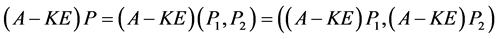
由于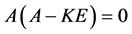 ,知
,知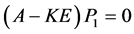 。所以
。所以
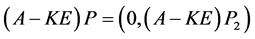 (2)
(2)
由(1)减去(2)得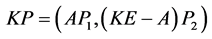 ,
,
注意到把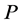 看成
看成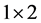 分块矩阵,将
分块矩阵,将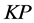 的第二列右乘以一个零矩阵0就等于
的第二列右乘以一个零矩阵0就等于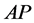 ,利用分块性质4,知
,利用分块性质4,知
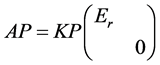
即
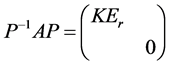
所以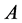 与对角矩阵
与对角矩阵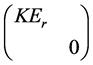 相似。
相似。
定理1 设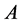 为
为 矩阵,且
矩阵,且 ,那么秩
,那么秩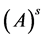 +秩
+秩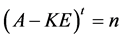 ,其中
,其中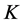 为任意给定的实数,
为任意给定的实数, 均为任意自然数。
均为任意自然数。
证:由引理1知
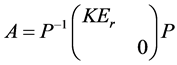 。
。
所以,
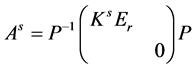 。
。
将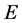 进行与
进行与 同样的分类,
同样的分类,
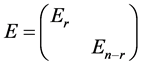 。
。
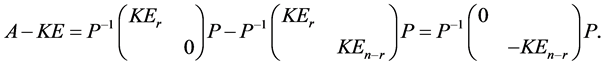

于是
秩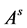 + 秩
+ 秩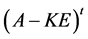 = 秩
= 秩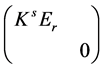 + 秩
+ 秩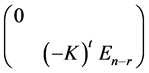 =
=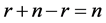 。
。
引理2设 为数域
为数域 上的一个
上的一个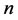 阶方阵,且满足
阶方阵,且满足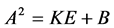 ,此时
,此时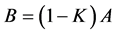 ,那么
,那么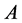 与对角矩
与对角矩
阵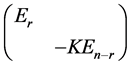 相似。
相似。
证:由 ,此时
,此时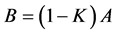 ,则
,则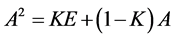 ,即
,即
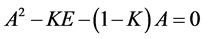 ,
,
所以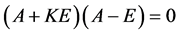 。
。
设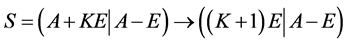 ,由性质2知
,由性质2知
秩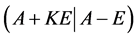 = 秩
= 秩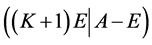 =
=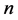 。
。
因此在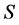 中存在
中存在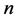 阶子式
阶子式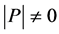 ,即矩阵
,即矩阵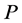 可逆,设
可逆,设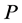 的前
的前 列所组成的子块
列所组成的子块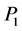 在
在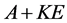 中,后
中,后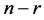 列所组成的子块
列所组成的子块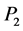 在
在 中,即
中,即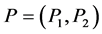 ,
,
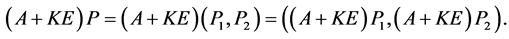
由于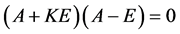 ,知
,知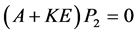 。
。
所以
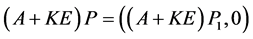 (3)
(3)
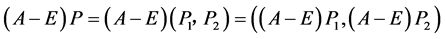
由于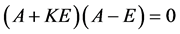 ,知
,知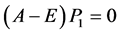 ,
,
所以
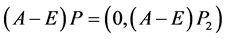 (4)
(4)
由(3)减去(4)得
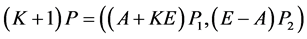
两边同乘以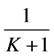 得
得
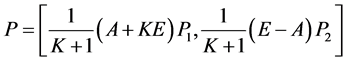
由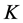 乘以(4)再加上(3)得
乘以(4)再加上(3)得
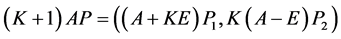
两边同乘以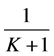 得
得
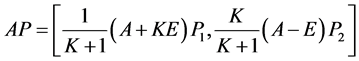
注意到把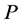 看成
看成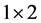 分块矩阵,将
分块矩阵,将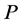 的第二列右乘
的第二列右乘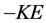 就等于
就等于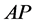 ,利用分块性质4,知
,利用分块性质4,知
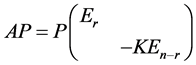
即
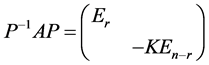
 .
.
所以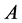 与对角矩阵
与对角矩阵 相似。
相似。
定理2 设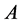 为
为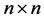 矩阵,且
矩阵,且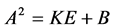 ,此时
,此时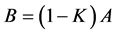 ,那么秩
,那么秩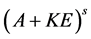 +
秩
+
秩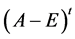 =
= ,其中
,其中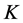 为任意给定的实数,
为任意给定的实数, 均为任意自然数。
均为任意自然数。
证:由引理2知
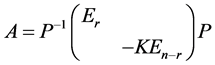
将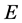 进行与
进行与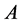 同样的分类得,
同样的分类得,

则
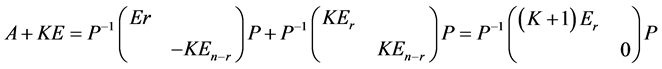 .
.
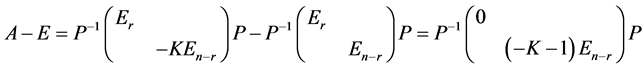 .
.
因此
 .
.
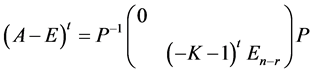 .
.
于是秩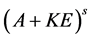 + 秩
+ 秩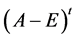 = 秩
= 秩 + 秩
+ 秩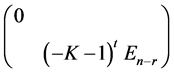 =
=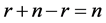 。
。
引理3 设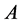 为数域
为数域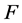 上的一个
上的一个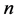 阶方阵,且满足
阶方阵,且满足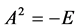 ,那么
,那么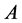 与对角矩阵
与对角矩阵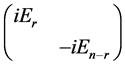 相似。
相似。
证:由 ,有
,有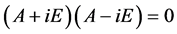 。
。
设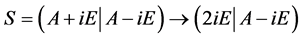 ,由性质2知秩
,由性质2知秩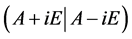 = 秩
= 秩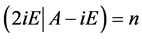 。
。
因此在 中存在
中存在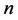 阶子式
阶子式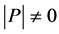 ,即矩阵
,即矩阵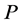 可逆。设
可逆。设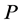 的前
的前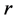 列所组成的子块
列所组成的子块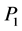 在子块
在子块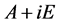 中,后
中,后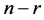 列所组成的子块
列所组成的子块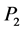 在
在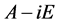 中,即
中,即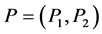 。
。
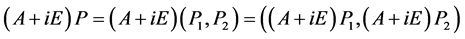
由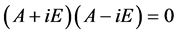 ,知
,知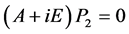 ,
,
所以
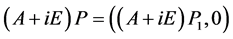 (5)
(5)
同理
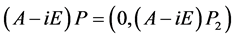 (6)
(6)
由(5)式加(6)式再同乘以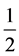 得
得
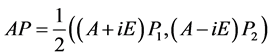
由(5)式减(6)式再同乘以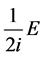 得
得
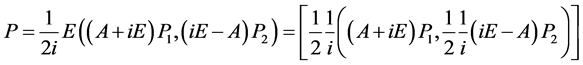
因此

从而
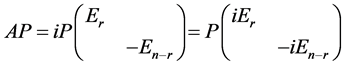
这意味着
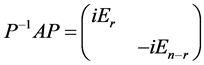
由此可知 与
与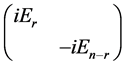 相似。
相似。
定理3 设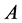 为
为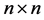 矩阵,且
矩阵,且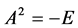 ,那么秩
,那么秩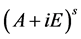 + 秩
+ 秩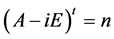 ,其中
,其中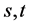 均为任意自然数。
均为任意自然数。
证:由引理3 知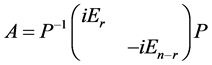 。
。
将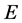 进行与
进行与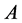 同样的分类,
同样的分类,
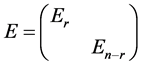 .
.
则
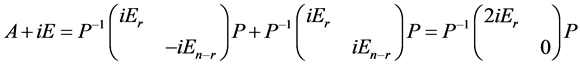 .
.
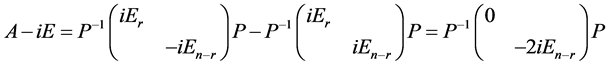 .
.
因此
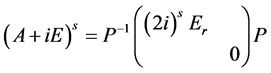 .
.
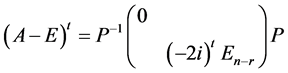 .
.
于是
秩 + 秩
+ 秩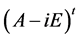 = 秩
= 秩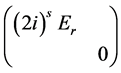 + 秩
+ 秩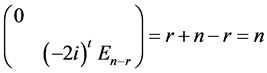 。
。
综合上述三种讨论可知,当对条件进行适当的推广时,能得到类似的结论。
基金项目
国家自然科学基金项目(11226167,11361020);海南省自然科学基金项目(111005)。
参考文献 (References)
- [1] 北京大学数学系几何与代数小组 (2003) 高等代数(第三版). 高等教育出版社, 北京, 162-203.
- [2] 雷雪萍 (2006) 高等代数中一道习题的推广. 大学数学, 4, 1-3.
- [3] 朱广振 (1999) 初等变换在线性代数中的应用. 辽宁工学院学报, 2, 1-2.
- [4] 高百俊 (2007) 分块矩阵的初等变换及其应用. 伊犁师范学报(自然科学版), 4, 14-18.
- [5] 邢铁磷 (1993) 矩阵初等变换的推广及其应用. 北京石油化学院学报, 1, 1-9.
- [6] 颜贵兴 (2006) 矩阵的初等变换及推广. 铁州学院学报, 6, 5-7.
- [7] 吴云 (1998) 分块矩阵的初等变换及其在求逆和行列式中的应用. 重庆工业管理学院学报, 3, 101-104