Pure Mathematics
Vol.05 No.02(2015), Article ID:14895,6
pages
10.12677/PM.2015.52004
Multiplicity of Positive Solutions for Kirchhoff Type of Equation with Hardy Singular Item
Hong Rong, Chunyu Lei, Hongmin Suo*
School of Science, Guizhou Minzu University, Guiyang Guizhou
Email: 402453552@qq.com, *gzmysxx88@sina.com
Received: Feb. 13th, 2015; accepted: Feb. 25th, 2015; published: Mar. 2nd, 2015
Copyright © 2015 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
In this paper, using the local minimum theorem and mountain pass lemma of variational methods, we study the Kirchhoff equation with Hardy singular term, and obtain multi- plicity results of solutions for this equation near resonance with principal eigenvalue.
Keywords:Kirchhoff Type of Equation, Hardy Singular Term, Variational Methods, Near Resonance

具有Hardy奇异项的近共振Kirchhoff方程正解的多重性
容红,雷春雨,索洪敏*
贵州民族大学理学院,贵州 贵阳
Email: 402453552@qq.com, *gzmysxx88@sina.com
收稿日期:2015年2月13日;录用日期:2015年2月25日;发布日期:2015年3月2日

摘 要
本文利用变分法中的局部极小定理和山路引理,研究了具有Hardy奇异项的Kirchhoff方程,从而得到了具有Hardy奇异项的Kirchhoff方程在主特征值处近共振问题解的多重性结果。
关键词 :Kirchhoff方程,Hardy奇异项,变分法,近共振

1. 引言
本文考虑下面的Kirchhoff方程
 (1)
(1)
其中 是具有光滑边界的有界开区域,
是具有光滑边界的有界开区域, ,
, ,
, 是实参数,
是实参数,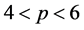 ,
,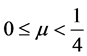 。
。
在方程(1)中,当 时,是通常具Dirichlet边值条件的Kirchoff型方程。
时,是通常具Dirichlet边值条件的Kirchoff型方程。
Ma et al. [1] 运用变分法得到了方程的正解。Zou [2] 使用局部极小原理和喷泉定理得到了方程非平凡解的存在性和多重性。特别地,Chen [3] 考虑下面的Kirchhoff方程

当参数 充分小时,得到上面方程至少存在三个正解。而对含Hardy奇异项的Kirchhoff方程目前还没有人研究。
充分小时,得到上面方程至少存在三个正解。而对含Hardy奇异项的Kirchhoff方程目前还没有人研究。
方程(1)对应的特征值问题
 (2)
(2)
其中,第一特征值 表示为
表示为
 (3)
(3)
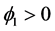 是对应于
是对应于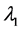 的特征函数。
的特征函数。 是Sobolev空间,它的范数是
是Sobolev空间,它的范数是 ,内积为
,内积为 ;
; 的范数是
的范数是 ;
; ,
, ;
; 是最佳Sobolev嵌入常数,即
是最佳Sobolev嵌入常数,即
 (4)
(4)
方程(1)的能量泛函表示为
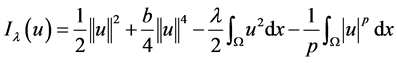 ,
, 。
。
通常,对任意的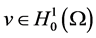 ,方程
,方程

成立时,则称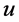 是(1)的解。
是(1)的解。
2. 预备知识
引理2.1 如果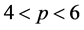 ,存在
,存在 充分小,则对任意的
充分小,则对任意的 ,存在
,存在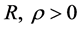 有
有
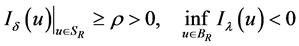 (5)
(5)
证明:由Hölder不等式和(4)式,有
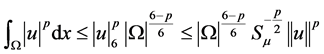 。 (6)
。 (6)
由于 和
和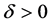 充分小时,有
充分小时,有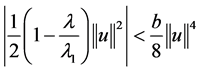 ,可得
,可得
 (7)
(7)
所以,由(3),(6)和(7),有
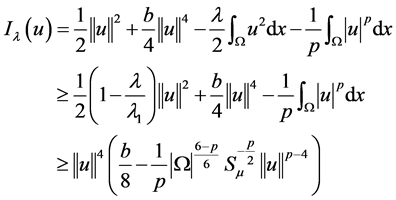
设 ,
,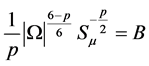 ,
, 有
有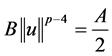 ,
, 。
。
因此,存在常数 ,
, 。所以,存在常数
。所以,存在常数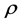 ,对任意
,对任意 ,有
,有 。
。
对给定的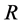 ,选择
,选择 且
且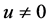 ,证明不等式
,证明不等式
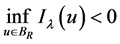 (8)
(8)
即就是对任意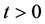 充分小,有
充分小,有 。事实上,由(2),有
。事实上,由(2),有 ,也可得
,也可得
 (9)
(9)
另一方面,方程 两边同乘
两边同乘 ,且在
,且在 上两边同时积分,可得
上两边同时积分,可得
 (10)
(10)
对任意的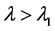 ,把(10)代入(9),可得
,把(10)代入(9),可得
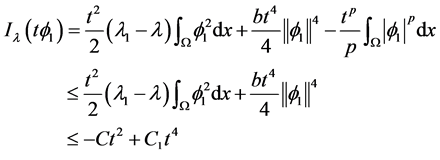
这里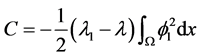 ,
, 。对所有的
。对所有的 充分小时,
充分小时,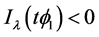 。因此,对给定的
。因此,对给定的 且
且 充分小时,对所有的
充分小时,对所有的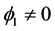 ,有
,有 ,证毕。
,证毕。
引理2.2 假设 ,存在正常数
,存在正常数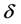 ,
,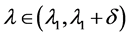 ,
,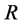 ,
,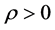 泛函
泛函 满足如下条件:
满足如下条件:
1)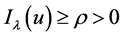 如果
如果 ;
;
2) 存在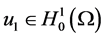 ,当
,当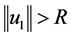 时,
时, ;
;
证明:
1) 由引理2.1,可知引理2.2的条件(1)成立,证毕。
2) 对任意的 ,
,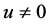 且
且 ,有
,有
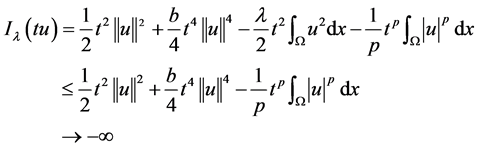
当 。因此,存在
。因此,存在 使得
使得 时,有
时,有 ,证毕。
,证毕。
引理2.3 假设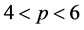 ,
, ,则对任意的
,则对任意的 ,泛函
,泛函 满足
满足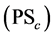 条件。
条件。
证明:当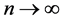 时,
时, 使得
使得
 (11)
(11)
要证 在
在 中是有界的。假设当
中是有界的。假设当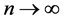 ,有
,有 。由(11)和(3)可知
。由(11)和(3)可知

上式得出矛盾。因此 在
在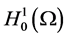 中是有界的,即存在
中是有界的,即存在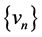 的一个子序列,仍记为
的一个子序列,仍记为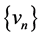 ,且存在
,且存在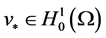 使得
使得
 在
在 中弱收敛于
中弱收敛于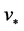 ,在
,在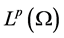 中强收敛于
中强收敛于 ,
, (12)
(12)
设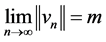 ,
,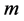 是一个正常数。由(11),(12),
是一个正常数。由(11),(12), ,可得
,可得
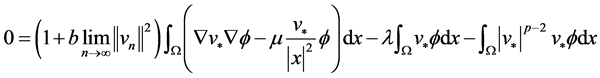 (13)
(13)
特别,对任意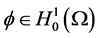 ,在(13)中选
,在(13)中选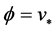 ,有
,有

上式两边当 取极限,可得
取极限,可得
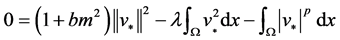 (14)
(14)
另一方面,当 充分大时,由(11)有,
充分大时,由(11)有,

上式两边当 取极限时,可得
取极限时,可得
 (15)
(15)
因此,由上面不等式(14)和(15),可知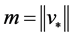 ,即
,即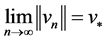 。则证明了当
。则证明了当 时,
时, 在
在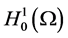 中有
中有 。综上所述,可知
。综上所述,可知 满足
满足 条件,证毕。
条件,证毕。
3. 主要结果及其证明
定理3.1 假设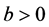 ,
, 。则存在
。则存在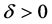 充分小,使得对任意的
充分小,使得对任意的 ,方程(1)在
,方程(1)在 中至少有两个不同的正解。
中至少有两个不同的正解。
证明:当 ,则对任意的
,则对任意的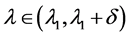 ,方程(1)有一个正解
,方程(1)有一个正解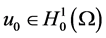 满足
满足 。事实上,由于
。事实上,由于 是一个闭球,这里定义
是一个闭球,这里定义
 (16)
(16)
由引理2.1,有 。对于给定的
。对于给定的 ,由(16),存在
,由(16),存在 且
且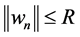 使得
使得

因此,根据Ekeland变分原理[4] ,存在 且
且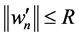 满足
满足

和
 (17)
(17)
当 时,序列
时,序列 满足
满足 ,
, 。再由引理2.1可知在
。再由引理2.1可知在 中,
中, 是泛函
是泛函 的一个局部极小解且
的一个局部极小解且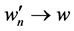 。因此,由(17),有
。因此,由(17),有 ,又因
,又因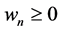 可知,当
可知,当 时,在
时,在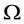 中有
中有 几乎处处成立,且是方程(1)的解。由强极大值原理可知:在
几乎处处成立,且是方程(1)的解。由强极大值原理可知:在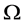 中,有
中,有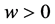 ,这里可选
,这里可选 即可。
即可。
另一方面,当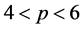 ,则对
,则对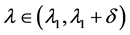 ,方程(1)有一个正解
,方程(1)有一个正解 满足
满足 。
。
事实上,由于 ,则由引理2.2和引理2.3可知,
,则由引理2.2和引理2.3可知,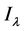 满足山路引理[5] 的几何结构,
满足山路引理[5] 的几何结构, 是
是 的一个临界值且
的一个临界值且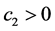 。因此,存在一个序列
。因此,存在一个序列 ,使得
,使得
 (18)
(18)
其中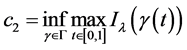
 ,且
,且
 。
。
由引理2.2,可得
 (19)
(19)
由引理2.3,可知 有一个收敛的子序列,仍记为
有一个收敛的子序列,仍记为 ,假设当
,假设当 时,
时, 在
在 中有
中有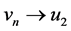 。因此由(18)和(19)有
。因此由(18)和(19)有
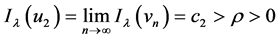 (20)
(20)
(20)式表明 。再由
。再由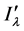 的连续性,可得
的连续性,可得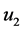 是(1)的一个解,即
是(1)的一个解,即
 (21)
(21)
对任意 。在(21)中取测试函数
。在(21)中取测试函数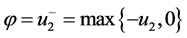 ,有
,有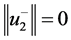 ,因此,
,因此, 且
且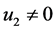 。
。
根据强极大值原理可知,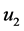 是(1)的一个正解,证毕。
是(1)的一个正解,证毕。
基金项目
贵州省科学厅自然科学基金资助项目([2013]2141号);黔教科研发[2013]405号;2014年贵州民族大学科研校级课题。
文章引用
容 红,雷春雨,索洪敏, (2015) 具有Hardy奇异项的近共振Kirchhoff方程正解的多重性
Multiplicity of Positive Solutions for Kirchhoff Type of Equation with Hardy Singular Item. 理论数学,02,21-27. doi: 10.12677/PM.2015.52004
参考文献 (References)
- 1. Ma, T.F. and Munoz Rivera, J.E. (2003) Positive solutions for a nonlinear elliptic transmission problem. Applied Ma-thematics Letters, 16, 243-248.
- 2. He, X. and Zou, W. (2010) Multiplicity of solutions for a class of Kirchhoff type problems. Acta Mathematicae Appllicatae Sinica, 26, 387-394.
- 3. Chen, J.Q. (2014) Multiple positive solutions to a class of Kirchhoff equation on with indefinite Nonlinearity. Nonlinear Analysis, 96, 134-145.
- 4. Aubin, T. and Ekeland, I. (1984) Applied nonlinear analysis. Wiley, New York.
- 5. Ambrosetti, A. and Rabinowitz, P.H. (1973) Dual variational methods in critical point theory and applications. Journal of Functional Analysis, 14, 349-381.