Pure Mathematics
Vol.05 No.04(2015), Article ID:15584,7
pages
10.12677/PM.2015.54019
The Analysis of Grazing Periodic Motions in a Single Degree of Freedom Vibro-Impact System with Double Constrains
Jieqiong Xu
College of Mathematics and Information Science, Guangxi University, Nanning Guangxi
Email: clh4@163.com
Received: Jun. 5th, 2015; accepted: Jun. 24th, 2015; published: Jun. 30th, 2015
Copyright © 2015 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
The stability of grazing periodic motion in a single degree of freedom vibro-impact system with double constrains is analyzed. The Poincaré mapping near the grazing trajectory is established by using the discontinuity mapping method. And the stability criterion of double grazing periodic motion is obtained. According to the criterion, it is demonstrated that local attractors do not exist near the double grazing trajectory, i.e., the grazing bifurcation is discontinuous. Finally, validity of the theoretical analysis is verified by the numerical results.
Keywords:Vibro-Impact System, Single Degree of Freedom, Grazing Motion, Discontinuity Mapping Method, Stability
一类双约束单自由度碰振系统的擦边运动分析
徐洁琼
广西大学数学与信息科学学院,广西 南宁
Email: clh4@163.com
收稿日期:2015年6月5日;录用日期:2015年6月24日;发布日期:2015年6月30日

摘 要
本文分析了一类单自由度双侧约束碰振系统的擦边周期运动的稳定性。利用不连续映射的方法建立了擦边周期轨道的局部Poincaré映射。在此基础上得到了双擦周期轨道的稳定性判据。根据此判据,可知系统在双擦周期轨道附近不存在局部吸引子,即,发生不连续擦边分岔。最后,用数值结果验证了理论方法的可行性。
关键词 :碰振系统,单自由度,擦边运动,不连续映射方法,稳定性

1. 引言
擦边现象存在于大量碰撞振动系统中。由于系统在擦边点处具有奇异性,导致系统有非常复杂的动力学行为。长期以来人们对碰振系统的擦边运动进行了广泛的研究。早在1983年,Shaw & Holmes [1] 在研究一个简谐激励下有约束的单自由度刚性碰撞振子时就最早发现了零速碰撞会导致奇异性的发生。Whiston [2] 在研究简谐激励下无阻尼线性冲击振子时,首先用奇异性理论研究了擦边碰撞的Poincaré映射不可微性,说明了碰撞振动的复杂运动形式与擦边现象具有内在的联系。Nordmark [3] 在这类单自由度碰振系统的研究中发现了擦边碰撞现象,并首次建立了冲击振子碰撞运动的Poincaré-Nordmark映射。Fredriksson和Nordmark [4] 推广了以前的工作,通过引入不连续映射建立起了多自由度冲击振子的Poincaré映射及规范型的计算,并推出了擦边轨道稳定的条件。Bernardo,Budd和Champneys [5] 用Nordmark不连续映射的方法推导出n维分段光滑动力系统在擦边轨道附近不连续映射的规范形,并用此来分析擦边分岔情况。在对称约束碰撞系统的研究方面,Foale、Bishop [6] 对一个双约束单自由度系统的擦边分岔进行了数值研究。A.C.J. Luo [7] 研究了一类具有双约束的非光滑动力系统的对称解。G.W. Luo [8] 等对一类对称双约束碰撞系统的Neimark-sacker分岔及环面分岔进行了研究并研究了此系统的余维二分岔。
本文在一个对称双擦周期轨道附近建立不连续映射,并用此分析了系统在擦边点处的局部分岔情况。
2. 模型
考虑由质量为m的振子组成的对称双约束单自由度碰振系统。振子由刚度为 的线性弹簧和阻尼系数为c的线性阻尼器相连接。质块只作水平方向的运动,并受简谐激励力
的线性弹簧和阻尼系数为c的线性阻尼器相连接。质块只作水平方向的运动,并受简谐激励力 的作用。处于平衡状态的振子与刚性约束A和B的距离为
的作用。处于平衡状态的振子与刚性约束A和B的距离为 。碰撞系统在没有碰撞时的无量纲运动方程为:
。碰撞系统在没有碰撞时的无量纲运动方程为:
 (2.1)
(2.1)
其中 ;
; ;
; 。且
。且 。振子的平衡位置为
。振子的平衡位置为 ,刚性约束A和B分别位于
,刚性约束A和B分别位于 和
和 ,所以距离d为单位长度。仍然用t来表示
,所以距离d为单位长度。仍然用t来表示 ,得到系统的运动方程为:
,得到系统的运动方程为:
 (2.2)
(2.2)
方程有一个特解:
 (2.3)
(2.3)
当 ;
; ;
; 。由此我们可以看出当
。由此我们可以看出当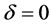 时系统存在双擦周期轨道
时系统存在双擦周期轨道 ,且
,且 可以看成是擦边分岔参数,因为当
可以看成是擦边分岔参数,因为当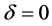 时,振子分别在
时,振子分别在 ,
, (
( ,2m + 1代表周期数)时发生擦边,当
,2m + 1代表周期数)时发生擦边,当 时,振子与分界面发生碰撞,当
时,振子与分界面发生碰撞,当 时,振子在
时,振子在 ,
, 都不碰。
都不碰。
方程的通解为:
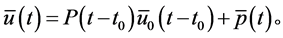 (2.4)
(2.4)
再由初始条件 得到方程的通解为:
得到方程的通解为:
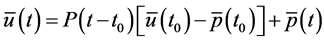 (2.5)
(2.5)
其中
 (2.6)
(2.6)
且 ,
, ,
, ,
, ,
, 。
。
3. 擦边周期运动不连续映射的推导
下面主要以周期1运动为例进行推导。由(2.6)式可知 的特征根为
的特征根为 ,
, ,所以当
,所以当 时系统的非碰周期轨道是渐进稳定的。令
时系统的非碰周期轨道是渐进稳定的。令
 (3.1)
(3.1)
其中特征值为 ,
, ,
, ,
, ,且
,且 。
。
下面我们来分析系统在双擦周期轨道附近的分岔情况。首先以相位面 为Poincaré截面。系统轨线如图1所示。当
为Poincaré截面。系统轨线如图1所示。当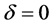 时,
时,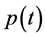 在
在 与分界面
与分界面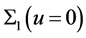 在
在 处发生擦边。当参数变化时,系统轨线与分界面发生碰撞,在碰撞函数的作用后与
处发生擦边。当参数变化时,系统轨线与分界面发生碰撞,在碰撞函数的作用后与 相交于
相交于 。我们假设当轨线到达分界面时,穿过分界面继续在系统流的作用下运动直到
。我们假设当轨线到达分界面时,穿过分界面继续在系统流的作用下运动直到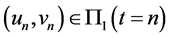 。那么从
。那么从 到
到 的映射
的映射 就是我们所要求的不连续映射
就是我们所要求的不连续映射 。
。
由(2.3)可知轨线在擦边点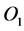 处的加速度为
处的加速度为 。把
。把 在
在 处展开到适当的阶数。
处展开到适当的阶数。
 (3.2)
(3.2)
其中
 由
由 得:
得: ,从而得到:
,从而得到: (3.3)
(3.3)

Figure 1. The impact map D1
图1. 碰撞映射D1
其中
 (3.4)
(3.4)
由(3.3)可知当 时系统发生碰撞,因为当
时系统发生碰撞,因为当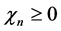 时(3.3)式才有解。根据不连续映射方法可得不连续映射
时(3.3)式才有解。根据不连续映射方法可得不连续映射 ,
,
当
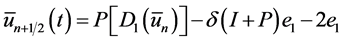 (3.5)
(3.5)
当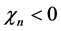
 (3.6)
(3.6)
其中I为单位矩阵, 。
。
当轨线运动到分界面 附近时,又需要考虑轨线与分界面的接触情况,同理可以建立不连续映射
附近时,又需要考虑轨线与分界面的接触情况,同理可以建立不连续映射 。
。
当
 (3.7)
(3.7)
当
 (3.8)
(3.8)
其中 。
。
由以上的推导可以建立双擦周期轨道附近的Poincaré映射 ,以
,以 为Poincaré截面,从一点
为Poincaré截面,从一点 出发(
出发( 且
且 在
在 的极小邻域内)
的极小邻域内) 。当
。当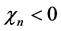 和
和 成立时,
成立时, 、
、 分别为恒等映射。
分别为恒等映射。
把(3.5),(3.6),(3.7),(3.8)写成矩阵形式为:
 (3.9)
(3.9)
 (3.10)
(3.10)
 (3.11)
(3.11)
 (3.12)
(3.12)
作下坐标变换,令 ,
, ,
, ,其中l为大于零的常数,
,其中l为大于零的常数, ,
,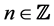 。并由上面坐标变化的4式可近似得到:
。并由上面坐标变化的4式可近似得到:
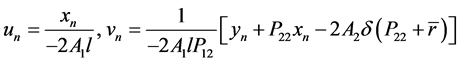
和

则(3.9)~(3.12)可简化为如下的形式:
对于 得:
得:
当 ,
,
 (3.13)
(3.13)
当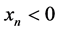 ,
,
 (3.14)
(3.14)
对于 得;
得;
当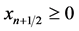 ,
,
 (3.15)
(3.15)
当 ,
,
 (3.16)
(3.16)
其中 ,
, ,
, 。
。

4. 双擦周期轨道的稳定性分析
由式(2.3)可以看出当 时系统存在双擦周期轨道
时系统存在双擦周期轨道 ,且当
,且当 变化时
变化时 会与分界面碰撞或者不碰,所以可以把
会与分界面碰撞或者不碰,所以可以把 看成是擦边分岔参数。由以上分析可知,以
看成是擦边分岔参数。由以上分析可知,以 为Poincaré截面,双擦周期轨道的Poincaré映射为
为Poincaré截面,双擦周期轨道的Poincaré映射为 ,
, 。当
。当 和
和 成立时,
成立时, 、
、 分别为恒等映射。由(3.13)~(3.16)可以看出当
分别为恒等映射。由(3.13)~(3.16)可以看出当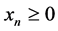 和
和 时,映射(3.13) (3.15)都含有平方根项,所以令
时,映射(3.13) (3.15)都含有平方根项,所以令 为擦边点,如果一点
为擦边点,如果一点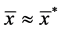 且
且 ,则
,则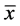 在映射(3.13) (3.15)的不断迭代下将不会向擦边点
在映射(3.13) (3.15)的不断迭代下将不会向擦边点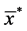 靠近,即在双擦周期轨道附近不会存在局部吸引子。
靠近,即在双擦周期轨道附近不会存在局部吸引子。
由(3.14) (3.16)可以得到它们的截尾映射:
 (4.1)
(4.1)
和
 (4.2)
(4.2)
其中A为一个矩阵,它的元素分别为 ,
,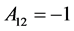 ,
, ,
, 。
。
如果要使双擦周期轨道附近存在局部吸引子,就需要满足从一点 且
且 出发,经过映射(3.13)得到
出发,经过映射(3.13)得到 且
且 ,
, 再经过映射(3.15)得到
再经过映射(3.15)得到 且
且 ,如果此后只满足映射(3.14) (3.16)条件,那么轨线将向擦边点
,如果此后只满足映射(3.14) (3.16)条件,那么轨线将向擦边点 靠近,即在双擦周期轨道附近存在局部吸引子。具体表示成式子就是
靠近,即在双擦周期轨道附近存在局部吸引子。具体表示成式子就是
如果 ,
, ,
, ,且对于任何
,且对于任何 ,
, 都有
都有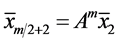 ,且
,且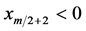 ,那么双擦周期轨道附近存在局部吸引子。
,那么双擦周期轨道附近存在局部吸引子。
下面我们对这个系统具体讨论,看在双擦周期轨道附近是否存在局部吸引子。由式(3.1)和系统的物理意义都可以得到 和
和 都是正数,那么当
都是正数,那么当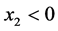 ,经过映射(4.1)得到
,经过映射(4.1)得到 ,
,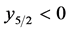 ,满足映射(4.2)的条件,经过映射(4.2),可以得到
,满足映射(4.2)的条件,经过映射(4.2),可以得到 ,这样就不能满足上面给出的条件,所以对这种双擦周期轨道其附近是不存在局部吸引子的。
,这样就不能满足上面给出的条件,所以对这种双擦周期轨道其附近是不存在局部吸引子的。
对原系统(2.2)取参数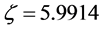 ,
, ,
, ,
, ,即
,即 ,对系统(2.2)仿真得到一个对称双擦周期1轨道如图2所示。系统的擦边状态属于临界情况,当系统参数变化时系统轨线与分界面就会出现碰或不碰的情况。变化参数令
,对系统(2.2)仿真得到一个对称双擦周期1轨道如图2所示。系统的擦边状态属于临界情况,当系统参数变化时系统轨线与分界面就会出现碰或不碰的情况。变化参数令 ,使
,使 ,仍对原系统(2.2)仿真得到一个对称双碰周期1轨道,如图3所示。接着我们讨论此对称双擦周期1轨道附近是否存在局部吸引子。用第三节求出的不连续映射(3.13~3.16)随着
,仍对原系统(2.2)仿真得到一个对称双碰周期1轨道,如图3所示。接着我们讨论此对称双擦周期1轨道附近是否存在局部吸引子。用第三节求出的不连续映射(3.13~3.16)随着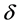 的变化作系统在此双擦周期1轨道附近的分岔图。如图4所示:当
的变化作系统在此双擦周期1轨道附近的分岔图。如图4所示:当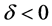 时,系统存在非碰周期1运动,当
时,系统存在非碰周期1运动,当 时,系统存在碰撞周期1运动,当
时,系统存在碰撞周期1运动,当 时系统发生擦边且系统在擦边点处发生了跳跃,这与我们上面得到的结果是一致的,在此双擦周期轨道附近不存在局部吸引子。变动参数f再对原系统(2.2)仿真,得到位移随参数f变化的分岔图。如图5所示:当
时系统发生擦边且系统在擦边点处发生了跳跃,这与我们上面得到的结果是一致的,在此双擦周期轨道附近不存在局部吸引子。变动参数f再对原系统(2.2)仿真,得到位移随参数f变化的分岔图。如图5所示:当 时,系统作非碰周期1运动,当
时,系统作非碰周期1运动,当 时,发生碰撞,为对称碰撞周期1运动,当
时,发生碰撞,为对称碰撞周期1运动,当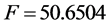 ,系统出现对称双擦运动且在擦边点处发生跳跃,这说明此双擦周期轨道附近不存在局部
,系统出现对称双擦运动且在擦边点处发生跳跃,这说明此双擦周期轨道附近不存在局部

Figure 2. Grazing period orbit of system (2.2)
图2. 系统(2.2)的擦边周期轨道

Figure 3. Impacting period orbit of system (2.2)
图3. 系统(2.2)的碰撞周期轨道

Figure 4. Bifurcation diagram of mapping system (
图4. 映射系统(

Figure 5. Bifurcation diagram of differential system (2.2)
图5. 原系统(2.2)的分岔图
吸引子。对原系统(2.2)仿真得到了与对不连续映射(3.13~3.16)仿真的一致结果,说明了不连续映射方法对此对称双擦周期轨道的有效性及不连续映射(3.13~3.16)的正确性。
5. 小结
本文对一个双侧约束的单自由度系统进行了分析,得到了一个对称双擦周期轨道,用不连续映射的方法推导出了此双擦周期轨道附近的不连续映射。并用此不连续映射分析了擦边分岔情况,得到了在此双擦周期轨道附近不存在局部吸引子的结论,并对原系统仿真说明了对双擦周期轨道运用不连续映射方法的有效性。
基金项目
广西自然科学基金(No. 2014GXNSFBA118024)资助。
文章引用
徐洁琼, (2015) 一类双约束单自由度碰振系统的擦边运动分析
The Analysis of Grazing Periodic Motions in a Single Degree of Freedom Vibro-Impact System with Double Constrains. 理论数学,04,121-128. doi: 10.12677/PM.2015.54019
参考文献 (References)
- 1. Shaw, S.W. (1985) The dynamics of a harmonically excited system having rigid amplitude constraints: part II-Chaotic motions and global biburcations. Journal of Applied Mechanics, 52, 459-464. http://dx.doi.org/10.1115/1.3169069
- 2. Whiston, G.S. (1992) Singularities in vibro-impact dynamics. Journal of Sound and Vibration, 152, 427-460. http://dx.doi.org/10.1016/0022-460X(92)90480-L
- 3. Nordmark, A.B. (1991) Non-periodic motion caused by grazing incidence in an impact oscillator. Journal of Sound and Vibration, 145, 279-297. http://dx.doi.org/10.1016/0022-460X(91)90592-8
- 4. Fredriksson, M.H. and Norddmark, A.B. (2000) On normal form calculations in impact oscillators. Proceedings of the Royal Society London A, 456, 315-329. http://dx.doi.org/10.1098/rspa.2000.0519
- 5. di Bernardo, M., Budd, C.J. and Champneys, A.R. (2001) Normal form maps for grazing bifurcation in n-dimensional piecewise-smooth dynamical systems. Physic D, 160, 222-254. http://dx.doi.org/10.1016/S0167-2789(01)00349-9
- 6. Foale, S. and Bishop, S.R. (1992) Dynamical complexities of forced impacting. Philosophical Transactions of the Royal Society London A, 338, 547-556. http://dx.doi.org/10.1098/rsta.1992.0020
- 7. Luo, A.C.J. (2004) On the symmetry of solution in non-smooth dynamical systems with two constraints. Journal of Sound and Vibration, 273, 1118-1126. http://dx.doi.org/10.1016/j.jsv.2003.09.011
- 8. Luo, G.W., Zhang, Y.L., Chu, Y.D. and Zhang, J.G. (2007) Co-dimension two bifurcations fixed points in a class of vibratory systems with symmetrical rigid stops. Nonlinear Analysis: Real World Applications, 9, 1272-1292. http://dx.doi.org/10.1016/j.nonrwa.2006.07.003