Pure Mathematics
Vol.06 No.02(2016), Article ID:17140,6
pages
10.12677/PM.2016.62013
A Note on the Definitions of Blocks of Epigroups
Qinqin Chen, Jingguo Liu*
School of Sciences, Linyi University, Linyi Shandong

Received: Feb. 28th, 2016; accepted: Mar. 9th, 2016; published: Mar. 16th, 2016
Copyright © 2016 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
A semigroup is called an epigroup if for any element in this semigroup some power of the element lies in the maximal subgroup of the given semigroup. In this paper two variants of definitions of blocks of semigroups are given and we prove that two of them turn out to coincide in the case of epigroups. We also offer the third definition of blocks of epigroups and show that if blocks of epigroups are subsemigroups, then this definition is equivalent to the other two.
Keywords:Epigroup, Block, Regular -Class
-Class

关于完全π-正则半群分块定义的一个注记
陈琴琴,刘靖国*
临沂大学理学院,山东 临沂

收稿日期:2016年2月28日;录用日期:2016年3月9日;发布日期:2016年3月16日

摘 要
完全π-正则半群是其所含任意元的某个幂属于其最大子群的半群。论文给出了两个不同形式的半群分块的定义,证明当所给半群为完全π-正则半群时这两个定义是等价的。论文还提供了分块的第三个定义,证明当分块为子半群时,完全π-正则半群的第三个分块定义与前两者等价。
关键词 :完全π-正则半群,分块,正则 -类
-类

1. 引言与预备知识
完全π-正则半群S是其所含任意元x的某个幂 (n为正整数)属于其最大子群
(n为正整数)属于其最大子群 的半群。包含元x的最大子群的单位元记作
的半群。包含元x的最大子群的单位元记作 。易知
。易知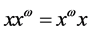 且
且 是
是 中的群元,其在
中的群元,其在 中的群逆元记
中的群逆元记 ,映射
,映射 称作是S上的伪逆运算。Shevrin的文献 [1] [2] 致力于完全π-正则半群的结构性理论研究(也见 [3] )。特别地,完全π-正则半群可以看作是伪逆运算为一元运算的一元半群。把完全π-正则半群看作是一元半群的思想最早在文献 [1] 提出,该方法表现在以下三个方面:提出问题,所讨论问题的结果陈述以及适当采取应用技巧。之后这种思想在后来的相关文献得到了新的发展,如文献 [4] - [8] 就采取这些方法研究该类半群。
称作是S上的伪逆运算。Shevrin的文献 [1] [2] 致力于完全π-正则半群的结构性理论研究(也见 [3] )。特别地,完全π-正则半群可以看作是伪逆运算为一元运算的一元半群。把完全π-正则半群看作是一元半群的思想最早在文献 [1] 提出,该方法表现在以下三个方面:提出问题,所讨论问题的结果陈述以及适当采取应用技巧。之后这种思想在后来的相关文献得到了新的发展,如文献 [4] - [8] 就采取这些方法研究该类半群。
半群分块的术语最早是定义在有限0-单半群上,见Graham [9] 。而研究较早而且研究充分的是关于有限半群的分块为群的结果,具体内容参见文献 [10] [11] 或参考书目 [12] [13] 的相关章节。需要指出的是,上述文献用不同的方式定义了有限半群的分块。本文第2节,我们将把文献 [11] [14] 中的两个不同的有限半群上的分块定义推广到完全π-正则半群(甚至一般半群上),证明了在完全π-正则半群情形下两个定义的等价性。最后在第3节,我们特别提到文献 [12] 分块的定义,指出并证明在特殊情况下,即分块为子半群的情形下,该定义和上述文献中的定义等价。
本文所用半群记号和术语详见参考文献 [15] - [19] 。下面给出本文需要的一些预备知识。
设a为半群S的一个元,元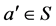 称为a在S中的逆元,若
称为a在S中的逆元,若 。元a在S中的逆元之集记为
。元a在S中的逆元之集记为 。半群S称为正则的,若S中的任一元都存在逆元。若
。半群S称为正则的,若S中的任一元都存在逆元。若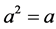 ,称a是S中的幂等元。若a属于S的一个子群,则称a是S中的群元。设a是S的子集,属于a的幂等元之集记为
,称a是S中的幂等元。若a属于S的一个子群,则称a是S中的群元。设a是S的子集,属于a的幂等元之集记为 ,而属于a的群元之集记为
,而属于a的群元之集记为 。由S的子集a生成的S的子半群记为
。由S的子集a生成的S的子半群记为 。设a与b为半群S的两个子集,集合
。设a与b为半群S的两个子集,集合 记为
记为 。假设a为半群S的一个理想(即
。假设a为半群S的一个理想(即 ),则
),则 表示半群S的Rees商。
表示半群S的Rees商。
 和
和 表示半群S上的Green关系,包含元a的
表示半群S上的Green关系,包含元a的 -类记作
-类记作 ,类似可记
,类似可记 及
及 。如果u为半群S的子半群,则对
。如果u为半群S的子半群,则对 ,
, 表示u中的Green关系,从而我们有记号
表示u中的Green关系,从而我们有记号
 。
。
称半群S的 -类d为正则的,若d中至少包含一个幂等元;此时d中任一元都是正则的。
-类d为正则的,若d中至少包含一个幂等元;此时d中任一元都是正则的。
下面重要的“定位”结果在后文中将会用到,来自( [19] ,命题2.3.7)。
引理1.1:令a,b是半群S的一个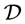 -类d中的元。则
-类d中的元。则 当且仅当
当且仅当 包含一个幂等元。
包含一个幂等元。
下述引理中的(i)~(iii)显然是( [16] ,定理6.45)的推论,在( [17] ,引理2.2)中有提及。
引理1.2:令S为一完全π-正则半群。则
(i) ;
;
(ii) 对 ,若
,若 ,则
,则 ;
;
(iii) 对 ,若
,若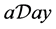 ,则
,则 。
。
令D为半群s的 -类。称凭借集合
-类。称凭借集合 ,0为零元,为D的迹,其运算*如下定义:对任意
,0为零元,为D的迹,其运算*如下定义:对任意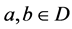 ,
,
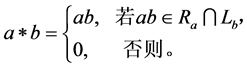
如果s为完全π-正则半群,则由引理1.2, 上的运算*可如下定义:对任意
上的运算*可如下定义:对任意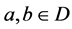 ,
,
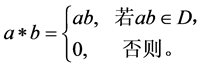
下面的引理来自( [17] ,引理II.2.5;命题II.4.8)。
引理1.3:令D为半群s的一个正则 -类,
-类, 为D的迹。
为D的迹。
(i) T的非零 -类为s的包含于D的非零
-类为s的包含于D的非零 -类;
-类;
(ii) T的非零 -类为s的包含于D的非零
-类为s的包含于D的非零 -类;
-类;
(iii) T为完全0-单半群。
2. 分块的两个定义及等价性证明
2.1. 分块的两个定义
下列命题来自( [11] ,定理3.1),在该文献中,分块是定义在有限0-单半群上,这儿同样可以证明该结论对一般的完全0-单半群也成立。
命题2.1:令 为完全0-单半群,
为完全0-单半群, 。则T的正则
。则T的正则 -类
-类 (
( ),称为
),称为 的分块,并具有如下性质:
的分块,并具有如下性质:
(i) 对任意 ;
;
(ii) 对任意 ;
;
(iii) 对任意 。
。
定义2.1:令D为半群s的正则 -类,则由引理1.3,D的迹
-类,则由引理1.3,D的迹 为完全0-单半群。从而我们定义
为完全0-单半群。从而我们定义 的分块为半群s的分块。
的分块为半群s的分块。
定义2.1':在上述定义中,如果不通过中介 ,我们也称半群
,我们也称半群 的正则
的正则 -类b为D的分块,并对s的分块b定义其商半群
-类b为D的分块,并对s的分块b定义其商半群 :
:
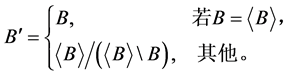
显然,如果 ,则b是S的分块,否则b的迹
,则b是S的分块,否则b的迹 是S的分块,为完全0-单半群。本文对
是S的分块,为完全0-单半群。本文对 不加区分(实际上,除了零元,二者具有同一凭借集合),都称为S的分块。
不加区分(实际上,除了零元,二者具有同一凭借集合),都称为S的分块。
Moura(见文献 [14] )也给出了有限半群S的分块的定义。下面我们叙述该定义,并且去掉该文献中有限半群条件的限制,推广到一般半群上。
令S为一半群,D为s的正则 -类。如下定义
-类。如下定义 上的等价关系“~”:
上的等价关系“~”:
 当且仅当存在幂等元链
当且仅当存在幂等元链 使得
使得 ,
,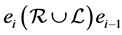 ,
, 。
。
包含元g的~类记作 ,根据该定义显然有
,根据该定义显然有 。
。
定义2.2:设D为半群S的一个正则 -类,由D中的一个
-类,由D中的一个 类生成的子半群模不属于D的元构成的理想,得到的Rees商称为D的分块。而S的所有正则
类生成的子半群模不属于D的元构成的理想,得到的Rees商称为D的分块。而S的所有正则 -类的分块称作S的分块。
-类的分块称作S的分块。
2.2. 定义2.1和定义2.2的等价性的证明
注意到对任意 ,
,
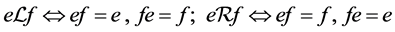 ,
,
并且 ,蕴含
,蕴含 是
是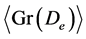 的子群。从而若
的子群。从而若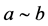 ,则
,则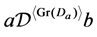 。这样我们可得如下结论。
。这样我们可得如下结论。
引理2.1:设D为半群S的一个正则 -类,
-类, 。对于
。对于 ,如果
,如果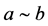 ,则
,则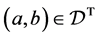 。
。
回到完全π-正则半群的情形,下面的定理显然给出两个定义的一致性。首先注意到分块b是 的一个正则
的一个正则 -类,则由( [19] ,命题2.3.2),
-类,则由( [19] ,命题2.3.2), 。
。
定理2.1:设D为完全π-正则半群S的一个正则 -类,并记
-类,并记 。则对于T的正则
。则对于T的正则 -类b以及
-类b以及 ,有
,有 。
。
证明:由分块的定义,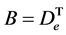 ,其中
,其中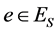 。任取
。任取 ,因为
,因为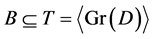 ,则形式上
,则形式上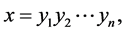 其中
其中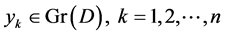 。再取
。再取 (注意到b正则,则
(注意到b正则,则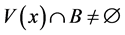 )。记
)。记
 。
。
显然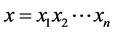 ,且
,且 ,这是因为
,这是因为

于是, ,即
,即 。另一方面,
。另一方面, ,即
,即 ,则由引理1.2
,则由引理1.2
 ,
,
这样 。易见
。易见 (既然
(既然 ,并且
,并且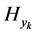 是D中的子群),从而
是D中的子群),从而 。现在
。现在 ,
, 。这样由引理1.2,元
。这样由引理1.2,元 和
和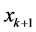 落入如下图所示的
落入如下图所示的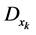 的“蛋壳”图。
的“蛋壳”图。

容易看出 ,这样
,这样 。现在对任意
。现在对任意 ,即
,即 ,如前所证,
,如前所证, ,其中
,其中 ,
, ,
, 。而
。而 蕴含着存在
蕴含着存在 使得
使得 ,并有
,并有 ,其中
,其中 ,
, ,特别有
,特别有 。但是由引理1.2,
。但是由引理1.2, ,从而
,从而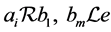 ,这当然蕴含着
,这当然蕴含着 ,
, 。既然
。既然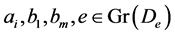 ,
, ,则有
,则有 。所以
。所以 ,从而
,从而 。结果
。结果 。
。
相反,令 ,其中
,其中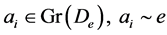 。则易证
。则易证 ,即
,即 。这样
。这样 。
。
3. 分块为半群的情形
文献 [12] 也定义了有限半群的分块的定义。下面我们给出该定义,注意这儿的半群不限于有限半群。
定义3.1:设D为半群S的一个正则 -类。称D的子集b为半群S的分块,若b为满足如下性质
-类。称D的子集b为半群S的分块,若b为满足如下性质
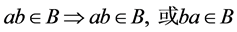
的D的最大子集。对S的分块b定义其商半群 :
:

由定义3.1,设D的子集b为半群S的分块,则对任意 ,对
,对 ,若有
,若有 或
或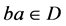 至少有一个成立,则由b的最大性,可得
至少有一个成立,则由b的最大性,可得 。
。
引理3.1:设b如定义3.1所给出的完全π-正则半群S的一个正则 -类D的分块,则
-类D的分块,则 。
。
证明:对任意 ,由定义3.1,
,由定义3.1, ,从而
,从而 ,由引理1.2,
,由引理1.2, ,再由( [19] ,定理2.2.5),
,再由( [19] ,定理2.2.5), 为S的子群,从而
为S的子群,从而 。这就证明了
。这就证明了 。
。 
注:由上述引理的证明,定义3.1中的分块都是s中的群元。
我们下面来证明定义3.1中的分块与定义2.2的关系。
命题3.2:令D为完全π-正则半群S的一个正则 -类,并记
-类,并记 。设
。设 是T的包含
是T的包含 正则
正则 -类,b包含g且为满足性质
-类,b包含g且为满足性质

D的最大子集。则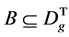 。
。
证明:设 ,则由引理3.1,
,则由引理3.1, ,又由B的性质有
,又由B的性质有 或者
或者 。不妨假定
。不妨假定 ,由引理1.2,
,由引理1.2, ,这样由引理1.1,存在
,这样由引理1.1,存在 使得
使得 ,这样就得到
,这样就得到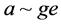 ,再由引理2.1,
,再由引理2.1, 。这就证明了
。这就证明了 。
。 
需要说明的是,一般情形下,定义2.2和定义3.1并不等价,考察如下半群:
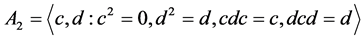 。
。
由定义2.2所定义的分块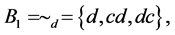 从而
从而 。而由定义3.1定义的分块
。而由定义3.1定义的分块 (或
(或 ),此时
),此时
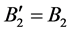 。显然二者不等。
。显然二者不等。
文献 [12] 所给分块定义主要考察分块为半群的情形,实际上,在命题3.2中分块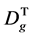 若为半群,则本文所给的三个定义等价,这是因为注意到命题3.2的结果
若为半群,则本文所给的三个定义等价,这是因为注意到命题3.2的结果 ,只要证
,只要证 即可。这是比较容易证明的,因为由命题3.2,
即可。这是比较容易证明的,因为由命题3.2, ,而当
,而当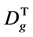 为半群,则对任意
为半群,则对任意 ,必有
,必有 ,由定义3.1中规定的b的最大性,可知一定有
,由定义3.1中规定的b的最大性,可知一定有 。
。
资助项目
该论文得到临沂大学校级大学生创新创业训练项目的支持(2015年度)。
文章引用
陈琴琴,刘靖国. 关于完全π-正则半群分块定义的一个注记
A Note on the Definitions of Blocks of Epigroups[J]. 理论数学, 2016, 06(02): 89-94. http://dx.doi.org/10.12677/PM.2016.62013
参考文献 (References)
- 1. Shevrin, L.N. (1995) On the Theory of Epigroups, I. Russian Academy of Sciences. Sbornik Mathematics, 82, 485-512. http://dx.doi.org/10.1070/sm1995v082n02abeh003577
- 2. Shevrin, L.N. (1995) On the Theory of Epigroups, II. Russian Academy of Sciences. Sbornik Mathematics, 83, 133-154. http://dx.doi.org/10.1070/sm1995v083n01abeh003584
- 3. Shevrin, L.N. (2005) Epigroups. In: Kudravtsev, V.B. and Rosenberg, I.G., Eds., Structural Theory of Automata, Semigroups, and Universal Algebra, Springer, Berlin, 331-380. http://dx.doi.org/10.1007/1-4020-3817-8_12
- 4. Liu, J.G. (2014) A Relation on the Congruence Lattice of an Epigroup. Advances in Mathematics (China), 43, 498-504.
- 5. Liu, J.G. (2013) Epigroups in which the Operation of Taking Pseudo-Inverse Is an Endomorphism. Semigroup Forum, 87, 627-638.
- 6. Liu, J.G. (2013) Epigroups in which the Relation of Having the Same Pseudo-Inverse Is a Congruence. Semigroup Forum, 87, 187-200. http://dx.doi.org/10.1007/s00233-012-9462-7
- 7. Liu, J.G. (2015) Epigroups in which the Idempotent-Generated Subsemigroups Are Completely Regular. Journal of Mathematical Research with Applications (China), 35, 529-542.
- 8. Liu, J.G., Chen, Q.Q. and Han C.M. (2016) Locally Completely Regular Epigroups. Communications in Algebra.
- 9. Graham, R.L. (1968) On Finite 0-Simple Semigroups and Graph Theory. Mathematical Systems Theory, 2, 325-339. http://dx.doi.org/10.1007/bf01703263
- 10. Margolis, S.W. and Pin, J.-E. (1985) Product of Group Languages. FCT Conference, Lecture Notes in Computer Science, 199, 285-299. http://dx.doi.org/10.1007/bfb0028813
- 11. Pin, J.-E. (1995) PG = BG: A Success Story. In: Fountain J., Ed., NATO Advanced Study Institute Semigroups, Formal Languages and Groups, Kluwer Academic, Dordrecht, 33-47. http://dx.doi.org/10.1007/978-94-011-0149-3_2
- 12. Almeida, J. (1994) Finite Semigroups and Universal Algebra (English Translation). World Scientific, Singapore.
- 13. Rhodes, J. and Steinberg, B. (2009) The q-Theory of Finite Semigroups. Springer, New York. http://dx.doi.org/10.1007/b104443
- 14. Moura, A. (2012) E-Local Pseudovarieties. Semigroup Forum, 85, 169-181. http://dx.doi.org/10.1007/s00233-012-9413-3
- 15. Clifford, A.H. and Preston G.B. (1961) The Algebraic Theory of Semigroups, Vol. I, Mathematical Surveys, No.7. American Mathematical Society, Providence.
- 16. Clifford, A.H. and Preston G.B. (1967) The Algebraic Theory of Semigroups, Vol. II, Mathematical Surveys, No.7. American Ma-thematical Society, Providence.
- 17. Grillet, P.A. (1995) Semigroups: An Introduction to the Structure Theory, Mo-nographs and Textbooks in Pure and Applied Mathematics, Vol. 193. Marcel Dekker Inc., New York.
- 18. Higgins, P.M. (1992) Techniques of Semigroup Theory. Oxford University Press, Oxford.
- 19. Howie, J.M. (1995) Fundamen-tals of Semigroup Theory. Clarendon, Oxford.