Pure Mathematics
Vol.07 No.02(2017), Article ID:19866,10
pages
10.12677/PM.2017.72008
Application of Transformation Method in Higher Algebra
Xiaofei Liu, Xiaojun Sun
School of Statistics and Mathematics, Yunnan University of Finance and Economics, Kunming Yunnan

Received: Feb. 15th, 2017; accepted: Mar. 2nd, 2017; published: Mar. 6th, 2017

ABSTRACT
Transformation method is one of the basic methods of mathematical methodology. From the direction of the transformation, this paper discusses the transformation method in the application of advanced algebra. Students should cultivate their thought of transformation consciously in the learning of advanced algebra knowledge.
Keywords:Transformation Method, Three Elements of Transformation, Transformation Direction
转化方法在高等代数中的应用
刘笑非,孙小军
云南财经大学统计与数学学院,云南 昆明
收稿日期:2017年2月15日;录用日期:2017年3月2日;发布日期:2017年3月6日

摘 要
转化方法是数学方法论中的基本方法之一,本文通过从转化的方向着手,探讨转化方法在高等代数中的具体应用。学生在学习高等代数知识的同时要有意识地培养转化的思想。
关键词 :转化方法,转化三要素,转化方向

Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
数学方法论中的转化思想是指把需要解决的问题通过某种转化过程,归结到一类已经能解决或者比较容易解决的问题中,最终获得问题的解答的一种思想方法 [1] 。转化的方法是指实现由所需要解决的问题向已经解决的或较易解决的问题的手段。每实现一次转化,都涉及到转化的对象、转化的方向和实现转化的方法 [2] 。我们把转化对象、方向、实现方法称之为转化的三要素。转化的对象是指变形的成分,在高等代数中一般有:将“未知”化为“已知”,一个关系转化为另一个关系,一个量转化为另一个量,一种运算转化为另一种运算等。转化的方向是指变形的目标 [3] ,一般有以下几种:化繁为简、化抽象为具体、化难为易、化综合为单一、化未知为已知等。实现转化的方法是指由所需要解决的问题向已经解决的或较易解决的问题转化的手段 [4] ,它包含特殊化法、一般化法、恒等变形法、分割法、添减法等。
2. 化繁为简
化繁为简是转化方法的基本方向之一,即就是将复杂的问题通过一些转化手段转化成较为简单的问题,先解决简单的问题然后再进行反演,再最后得到原问题的解。
在高等代数中,化繁为简应用十分广泛,例如,在线性方程与二次型中,将繁杂的解题过程,转化成较为简单的矩阵计算。
例1.1解下列方程组
 (1)
(1)
解设线性方程组(1)的增广矩阵为 ,则
,则

对 进行初等变换有:
进行初等变换有:

因为秩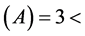 秩
秩 ,
,
故原方程组(1)无解。
分析本题的线性方程组中有四个未知数的线性方程 ,解这四个方程时,每
,解这四个方程时,每
一步都有重复的未知数 ,这就使得解题过程十分繁杂,而我们知道在解方程过程中,实际上是系数在变化,那么就可以通过线性方程组与矩阵的联系,其转化成较简单的增广矩阵
,这就使得解题过程十分繁杂,而我们知道在解方程过程中,实际上是系数在变化,那么就可以通过线性方程组与矩阵的联系,其转化成较简单的增广矩阵 ,再对增广矩阵
,再对增广矩阵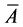 进行化简,这样解的过程就变得较为简单了。
进行化简,这样解的过程就变得较为简单了。
例1.2化下列二次型为标准形:

解 写出二次型的系数矩阵 ,就将繁杂的二次型问题化为较为简单的矩阵问题。
,就将繁杂的二次型问题化为较为简单的矩阵问题。
 ,
,
然后对 进行简化
进行简化

根据矩阵 ,设出过渡量
,设出过渡量
令
从而得到二次型的标准形为:
 。
。
分析上式的二次型若用配方法则过程由于要重复的写 ,而
,而 又是不变的,所以解题过程就相当繁杂,我们可以将繁杂的部分去掉,只考虑简单的系数,即将
又是不变的,所以解题过程就相当繁杂,我们可以将繁杂的部分去掉,只考虑简单的系数,即将
 转化成矩阵
转化成矩阵 进行,所求出的
进行,所求出的
就是标准形的系数矩阵。
3. 化抽象为具体
在高等代数中,抽象的概念让我们难以理解,同样,在解题中抽象的题目也让我们无从下手,这就需要我们运用转化的方法将抽象的问题化为具体的问题,通过求解具体的问题,从而得到原问题的解。
例2.1 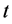 取什么值时,下列二次型是正定的
取什么值时,下列二次型是正定的
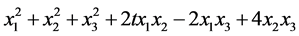
分析要证明二次型正定,可以通过定义将抽象的二次型正定转化成其对应矩阵正定,即将抽象的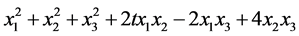 转化成具体的对称矩阵
转化成具体的对称矩阵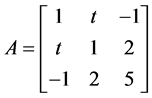 ,对矩阵进行求解化简。
,对矩阵进行求解化简。
解 二次型的矩阵为

由实二次型 是正定的充要条件为矩阵
是正定的充要条件为矩阵 的顺序主子式全大于零可知,当
的顺序主子式全大于零可知,当 的所有顺序主子式都大于0时,即
的所有顺序主子式都大于0时,即
 时,原二次型为正定矩阵的,联立得
时,原二次型为正定矩阵的,联立得 解得
解得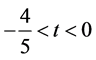 ,所以当
,所以当 时,该二次型正定。
时,该二次型正定。
在线性变换中,转化方法用得比较多,而化抽象为具体的应用主要在证明一些变换的特征值或变换是否可逆中。
例2.2 设A是线性空间 上的可逆变换,证明:A的特征值一定不为零。
上的可逆变换,证明:A的特征值一定不为零。
解析A 是可逆变换是抽象的,要直接找出它的特征值是十分困难的,而由变换与矩阵的联系,可将线性变换问题转化成矩阵问题求解,即将抽象的可逆变换A转化成具体的矩阵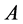 ,通过求解
,通过求解 的特征多项式来确定
的特征多项式来确定 是否等于0,从而得到
是否等于0,从而得到 的特征值,再反演成线性变换的特征值。
的特征值,再反演成线性变换的特征值。
证明 设与可逆变换A对应的矩阵为 ,则矩阵
,则矩阵 可逆,
可逆, 的特征多项式
的特征多项式

因为 可逆,故
可逆,故 ,又因为
,又因为 的特征值就是
的特征值就是 的全部根,这些根的积等于
的全部根,这些根的积等于 ,故A的特征值一定不为零。
,故A的特征值一定不为零。
而同样,在欧几里得空间中,在证明两个欧式空间同构时,也常用到化抽象为具体,将抽象的同构问题转化成空间的维数问题,进而转化成两组向量秩的问题。
例2.3 设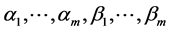 为
为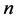 维欧式空间
维欧式空间 的两组向量,证明:若
的两组向量,证明:若 ,则
,则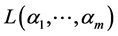 与
与 同构。
同构。
分析 要证抽象的二维向量构成的空间 与
与 同构,只需证它们维数相等,等价于这两个向量组的秩相等,即将抽象的两组向量构成的空间
同构,只需证它们维数相等,等价于这两个向量组的秩相等,即将抽象的两组向量构成的空间 与
与 同构转化成具体的维数跟秩的相等。
同构转化成具体的维数跟秩的相等。
证明 令 为
为 的一个极大线性无关组,
的一个极大线性无关组, 为其秩,
为其秩, ,则
,则
 ,
,
由于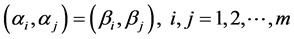 ,推知
,推知
 ,
,
进而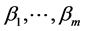 线性无关,因此维
线性无关,因此维 ,
,
即维 维
维 ,
,
同理可证维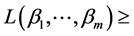 维
维 ,
,
所以 与
与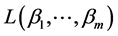 的维数相等,因此,它们同构。
的维数相等,因此,它们同构。
4. 化难为易
难和易是对立统一的,它们既相互联系又相互区别,化难为易在高等代数中的应用主要是反证法和行列式、矩阵的运算,具体如下:
例3.1证明: 不能有重根。
不能有重根。
分析要证明 不能有重根,只要证明
不能有重根,只要证明 ,而要证明
,而要证明
 比较难,我们常用的方法就是正难则反,从反面入手,只需设出
比较难,我们常用的方法就是正难则反,从反面入手,只需设出 的重根,求出它的值,看它是否是
的重根,求出它的值,看它是否是 的根。
的根。
证明 (反证法)令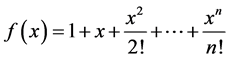 ,则
,则

假设 是
是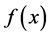 的一个重根,则有
的一个重根,则有

从而可得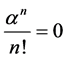 ,进而
,进而 ,但是零不是
,但是零不是 的根,矛盾。故
的根,矛盾。故
 不能有重根。
不能有重根。
例3.2 计算行列式
分析行列式 不是我们常规的行列式,
不是我们常规的行列式,
解 令

则
 ,
,
故当 时,秩
时,秩 ,故
,故 。
。
例3.3如果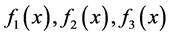 是线性空间
是线性空间 中三个互素的多项式,但其中任意两个都不互素,那么它们线性无关。
中三个互素的多项式,但其中任意两个都不互素,那么它们线性无关。
分析要证明 线性无关,而条件就只有
线性无关,而条件就只有 其中任意两个都不互素,而
其中任意两个都不互素,而 又没有具体的表达式,从正面入手比较难,那么就考虑反面,假定
又没有具体的表达式,从正面入手比较难,那么就考虑反面,假定 线性相关,根据线性相关的定义,只需证明是否存在三个不全为零的数
线性相关,根据线性相关的定义,只需证明是否存在三个不全为零的数 ,使
,使 ,解此式子则较为简单。
,解此式子则较为简单。
证明 (反证法)假定 线性相关,则存在不全为零的数
线性相关,则存在不全为零的数 ,使
,使

不妨设 ,那么有
,那么有
 ①
①
又因为 互素,所以存在多项式
互素,所以存在多项式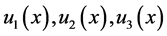 ,使
,使
 ②
②
将①式代入②式,得
 ,
,
因此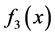 与
与 互素,这与已知矛盾,故
互素,这与已知矛盾,故 线性无关。
线性无关。
5. 化一般为特殊
特殊与一般是对立的统一,高等代数的学习和研究中特殊与一般是可以相互转化的,例如在证明多项式整除问题中,可以通过找出特殊值如公共根,特殊根等进行证明,再将结果推广到一般情形;在行列式、矩阵证明中应用的数学归纳法也是将一般转化成特殊情况进行。
例4.1 证明:如果 ,那么
,那么 。
。
分析 由于 是一次,而
是一次,而 是
是 次,如果直接入手很难,观察
次,如果直接入手很难,观察 可知,1是
可知,1是 的根,又
的根,又 ,所以可取特殊值
,所以可取特殊值 进行证明。
进行证明。
证明 由于 ,则有1是
,则有1是 的根,即
的根,即
 ,
,
这说明1是 的根,即
的根,即 。于是存在多项式
。于是存在多项式 ,
,
使得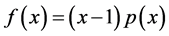 ,进而有
,进而有 ,所以
,所以 。
。
[5] 例4.2证明: 。
。
[6] 证明 (数学归纳法)
当 时,左边
时,左边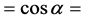 右边;
右边;
当 时,左边
时,左边 右边,
右边,
假设对于一切阶数小于 的行列式等号都成立,下证
的行列式等号都成立,下证 阶行列式的情形:
阶行列式的情形:
记 阶行列式为
阶行列式为 ,按最后一行展开,得
,按最后一行展开,得
由归纳假设可知,有
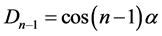 ,
,
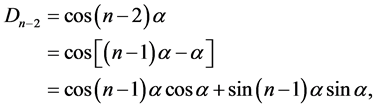
所以
故结论得证。
注 本题采用的是化一般为特殊中常用的数学归纳法,通过找出特殊的行列式的规律,总结推知一般情况。
例4.3 计算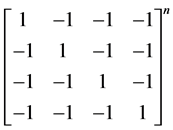
分析 要求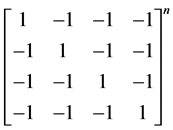 ,可以转化成求出
,可以转化成求出 的特殊方幂,即求出
的特殊方幂,即求出 幂的一个值使得它成为较为易求的矩阵,通过计算我们可以找出
幂的一个值使得它成为较为易求的矩阵,通过计算我们可以找出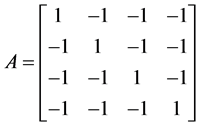 的2次幂是一个数量矩阵且与2的次幂有关,就可以将其转化成
的2次幂是一个数量矩阵且与2的次幂有关,就可以将其转化成 ,再通过它与n 次幂的关系,求出最终解。
,再通过它与n 次幂的关系,求出最终解。
解 令 ,则
,则
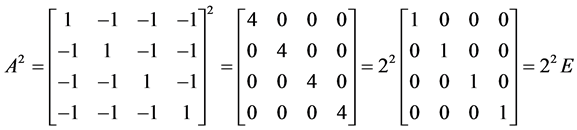
当 为偶数时,设
为偶数时,设 ,有
,有
 (取正整数)
(取正整数)
当 为奇数时,设
为奇数时,设 有,
有,
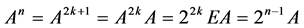 (取自然数)
(取自然数)
6. 化综合为单一
综合是由许多单一的部分通过某些联系而构成的复杂体,而单一则是一个个简单的事物部分。高等代数解题中,综合的问题一般都难以解答,就需要将其转化成一个个单一的问题,然后逐一解决,从而得到原问题的解。
在高等代数中,这一方法应用比较广泛。如,在线性空间与线性变换的特征值与特征向量的求解中,可以利用特征多项式,将其转化成求各个特征值的对应特征向量进行。
[5] 例5.1 设 ,
,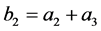 ,
,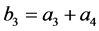 ,
, ,证明:向量组
,证明:向量组 ,
, ,
, ,
, 线性相关。
线性相关。
分析本题要证明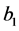 ,
,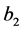 ,
, ,
,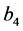 线性相关,关键在
线性相关,关键在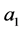 ,
, ,
, ,
, 是否线性相关上,而
是否线性相关上,而 ,
, ,
,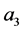 ,
, 的线性相关性题目中未给出,那么就需要我们进行分情况讨论,就把原问题转化成
的线性相关性题目中未给出,那么就需要我们进行分情况讨论,就把原问题转化成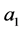 ,
, ,
, ,
, 线性相关或线性无关两个问题,然后逐一解决。
线性相关或线性无关两个问题,然后逐一解决。
[6] 证明 设 ,即
,即
 .
.
1)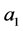 ,
,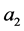 ,
,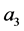 ,
,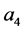 线性相关,则存在不全为零的数
线性相关,则存在不全为零的数 ,
, ,
, ,
,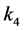 ,使得
,使得
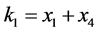 ,
,  ,
,  ,
, .
.
由 ,
, ,
, ,
, 不全为零知,
不全为零知, ,
, ,
,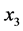 ,
, 不全为零,即
不全为零,即 ,
, ,
,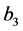 ,
, 线性相关。
线性相关。
2) ,
, ,
, ,
,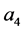 线性无关,则
线性无关,则
 ,
,
由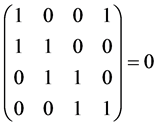 知,此齐次线性方程组存在非零解,则
知,此齐次线性方程组存在非零解,则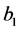 ,
, ,
,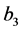 ,
, 线性相关。
线性相关。
综合1) 2)得证。
例5.2设 ,且
,且 ,
,
令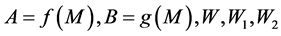 分别为线性方程组
分别为线性方程组 的解空间,证明:
的解空间,证明: 。
。
分析:证明 是一个较为综合的问题,我们可以把它分解成先证明
是一个较为综合的问题,我们可以把它分解成先证明 与
与 相等,再证明
相等,再证明 是直和,这样问题就简单化了。
是直和,这样问题就简单化了。
证明:① 先证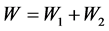
设 ,即
,即 ,从而
,从而

故 ,即
,即
 (1)
(1)
又由于 ,故
,故 ,使得
,使得 ,从而有
,从而有
 ,即
,即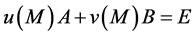
这样 ,有
,有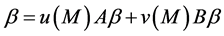
令 ,此时有
,此时有


即 ,故
,故 ,即
,即
 (2)
(2)
综合(1)式和(2)式得

再证 直和
直和
 ,由前知
,由前知
有 即
即
 ,所以
,所以 直和
直和
综上知
转化方法在高等代数中的应用是十分的广泛,充分的理解转化方法在高等代数中的应用,能让我们对转化方法有系统的认识,并且能锻炼我们的思维能力,提高我们的解题能力和运用能力。
文章引用
刘笑非,孙小军. 转化方法在高等代数中的应用
Application of Transformation Method in Higher Algebra[J]. 理论数学, 2017, 07(02): 51-60. http://dx.doi.org/10.12677/PM.2017.72008
参考文献 (References)
- 1. 北京大学数学系几何与代数教研室前代数小组. 高等代数(第三版)[M]. 北京: 高等教育出版社, 2003.
- 2. 邹本. 化归方法与高等代数教学[J]. 泰安师专学报(自然科学版), 1998(12): 11-16.
- 3. 林桂君. 谈高等数学中的转化方法[J]. 呼伦贝尔学院学报, 2008(6): 16-23.
- 4. 江小涛, 肖学平. 数学中的转化思想[J]. 三明大学学报, 1997(10): 2.
- 5. 刘振宇. 高等代数的思想与方法[M]. 济南: 山东大学出版社, 2009.
- 6. 闫晓红. 高等代数全程导学及习题全解(北京大学第三版)[M]. 北京: 中国时代经济出版社, 2006.