Modern Physics
Vol.4 No.06(2014), Article ID:14314,12 pages
DOI:10.12677/MP.2014.46016
Chaos Structured by Mixing of Multi-Excited Source
Electrical Engineering School of Guangxi University, Nanning
Email: *gxuhbh@163.com
Copyright © 2014 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received: Oct. 6th, 2014; revised: Oct. 28th, 2014; accepted: Nov. 4th, 2014
ABSTRACT
The solutions of dynamical system expressed with nonlinear differential equation
usually is shown by using time function . But this is not
unique mode, when particularly
. But this is not
unique mode, when particularly
 cannot be solved. In the modern theory of circuit and system, we can select three
dynamical variables in the nonlinear system to constitute 3-dimension phase space.
The mutual nonlinear relation among three dynamical variables can be described by
a bounded space curve. This is 3-dimension phase portrait. The nonlinear dynamical
systems of regarding
cannot be solved. In the modern theory of circuit and system, we can select three
dynamical variables in the nonlinear system to constitute 3-dimension phase space.
The mutual nonlinear relation among three dynamical variables can be described by
a bounded space curve. This is 3-dimension phase portrait. The nonlinear dynamical
systems of regarding
 variation may constitute
variation may constitute
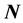 -dimension Euclidean space. The bounded space curve
cannot be represented by concretely explicit parametric form in math. It cannot
be solved analytically by human. However, the graphic solution can be plotted by
numerical simulation. If the bounded space curve is non-periodic in simulation interval,
this is orbital chaos of continuous time system. This paper researches the produce
and property of chaos by means of the analysis method of frequency domain and theorem
of power balance. We prove that the second order differential circuit which is constituted
by mixing of multi-excited source with different frequency also can produce chaos.
-dimension Euclidean space. The bounded space curve
cannot be represented by concretely explicit parametric form in math. It cannot
be solved analytically by human. However, the graphic solution can be plotted by
numerical simulation. If the bounded space curve is non-periodic in simulation interval,
this is orbital chaos of continuous time system. This paper researches the produce
and property of chaos by means of the analysis method of frequency domain and theorem
of power balance. We prove that the second order differential circuit which is constituted
by mixing of multi-excited source with different frequency also can produce chaos.
Keywords:Mixing, Chaos, Phase Portrait, Space Curve, Nonlinear Coupling, Frequency Domain

多激励源混频构成的混沌
黄炳华*,梁永清,韦忠海
广西大学电气工程学院,南宁
Email: *gxuhbh@163.com
收稿日期:2014年10月6日;修回日期:2014年10月28日;录用日期:2014年11月4日

摘 要
描写动态系统非线性微分方程的解,传统习惯于用时间函数 表示,但这不是唯一的方式,特别是当
表示,但这不是唯一的方式,特别是当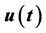 的表达式解不出来的时候。现代的电路与系统理论,在动态系统中,选取合适的三个动态变量组成一个三维的相空间,三个变量相互间的非线性关系,可以用一条有界的空间曲线来描写,这就是三维的相图。对于
的表达式解不出来的时候。现代的电路与系统理论,在动态系统中,选取合适的三个动态变量组成一个三维的相空间,三个变量相互间的非线性关系,可以用一条有界的空间曲线来描写,这就是三维的相图。对于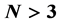 个变量可以组成
个变量可以组成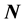 维的欧氏空间。这条有界的空间曲线,在数学上,不能用具体明显的参数式表达,我们不能求出其解析解。但可以用数值仿真画出它的图形解。如果这条有界的空间曲线在仿真的时间内是非周期的,这就是连续时间系统的轨道混沌。本文用频域的分析方法与功率平衡定理,研究混沌函数的诞生与属性。证明具有不同频率的多个激励源的混频,构成二阶微分电路也可以产生混沌。
维的欧氏空间。这条有界的空间曲线,在数学上,不能用具体明显的参数式表达,我们不能求出其解析解。但可以用数值仿真画出它的图形解。如果这条有界的空间曲线在仿真的时间内是非周期的,这就是连续时间系统的轨道混沌。本文用频域的分析方法与功率平衡定理,研究混沌函数的诞生与属性。证明具有不同频率的多个激励源的混频,构成二阶微分电路也可以产生混沌。
关键词
混频,混沌,相图,空间曲线,非线性耦合,频域

1. 引言
在两个变量构成的直角坐标相平面(或称状态平面)上,画出相点连续运动的相轨迹。用相图显示两个动态变量相互间的非线性函数关系,用这种平面相图作为方程的求解结果。这在混沌科学尚未诞生前,上世纪的五十年代就已经在非线性微分方程中广泛应用。例如范德堡振荡的平面相图是一个闭合的周期轨,这个典型的稳定极限环,至今学术界还无法写出它的解析解(有一些定性的近似解,也仅仅是描写相点进入极限环后的稳态解,进入极限环前起始暂态过程的解析解描写不出来),但它的图形解却很完美的征服了学术界,获得广泛承认。
在人类文明发展的历史长河中,不泛用图形解来代替解析解,推进了自然科学的向前发展。当今的混沌相图,作为非线性微分方程的图形解,在推进非线性动态科学的发展过程中,再一次充当了这种角色。
相图是微分方程的图形解,它显示了动态变量间的函数关系,推广到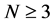 维相空间的典型实例,如三维系统Lorenz方程或蔡氏电路,描写这两个动态系统的微分方程如式(1),其解析解的参数式如式(2)。
维相空间的典型实例,如三维系统Lorenz方程或蔡氏电路,描写这两个动态系统的微分方程如式(1),其解析解的参数式如式(2)。
 (1)
(1)
 (2)
(2)
无法求出它的具体形式,只能用数值仿真画出其图形解,这显然是一条空间曲线,它是三个动态变量相互关系的非线性函数,这就是混沌函数。有一些能写出具体表达式被收入数学手册的空间曲线,是三变量函数的特殊形式,其空间图形有较明显的规律。恰恰是写不出表达式的混沌函数,才是三变量函数的普遍形式。其空间曲线的变化并非随机无规律的,式(2)空间曲线的变化规律受式(1)的约束[1] 。
混沌相图是求不出解析表达式的微分方程的图形解,人类依靠这个图形解推进了非线性动态科学的发展,这就是混沌科学。用三维直角座标的空间曲线表示三个动态变量的相互函数关系,其有关的定义,概念,推理和结论可以推广到多维的欧氏空间。非线性电路网络的微分方程写得出来,但求不出来,它的解是一个有界的非线性函数,这样的网络在电路中千千万万,可以在这样的网络中,选出三个或以上的动态变量,构造出三维或以上的混沌方程,一方面可用数值仿真画出其混沌的相图,论证这种网络诞生混沌的普遍性。另方面又可用频域的分析方法与功率平衡定理,近似的求出方程解的主体基本部份,相互印证求解结果的正确性[2] -[4] 。所指千千万万网络中,有如文献[5] [6] 介绍的无损耗网络,事实上是自激振荡与外加激励源在非线性电感中的混频。
2. 含多谐波激励源的电路网络诞生混沌
本文举出两个例证,说明电路网络包含不同频率的三个激励源,在非线性元件中混频会诞生混沌。
例1:电路如图1,由四条垂直支路 的KCL可列出式(3);由中间网孔的KVL可列出式(4);以(4)代入(3),并经整理化简可得式(5),图中各元件的参数如式(6)。
的KCL可列出式(3);由中间网孔的KVL可列出式(4);以(4)代入(3),并经整理化简可得式(5),图中各元件的参数如式(6)。
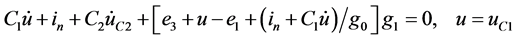 (3)
(3)
 (4)
(4)
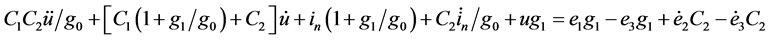 (5a)
(5a)
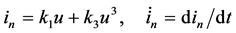 (5b)
(5b)
 (6a)
(6a)
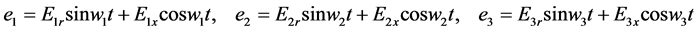 (6b)
(6b)
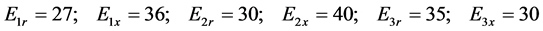 (6c)
(6c)
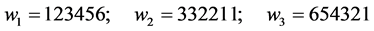 (6d)
(6d)
二阶非自治方程式(5)的解可以参考参照线性理论,其中一部份是当等式右边激励项等于零时,和起始状态有关的齐次解或称自由分量(或自然响应)。另部份是方程的特解或称强迫解,它取决于方程右边的激励项,和起始状态无关,线性方程的完全解是两部份解的线性迭加。而非线性方程(5)的解应该是这两部份解的非线性耦合。然而非线性方程自由分量的解析解是求不出的,因为它是耦合解的一部份,显然不可能单独求出来。
以下分析,随着谐波源成份的逐步增加,网络受迫振荡性状的演变,最后会诞生混沌。
1) 令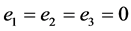 ,求无激励在一定起始条件下,式(5)的自由分量,是一条趋于零的渐近曲线,其中两个投影平面相图如图2。自由分量最终要衰减为零,故有时又称暂态响应,受迫解有时又称稳态响应
,求无激励在一定起始条件下,式(5)的自由分量,是一条趋于零的渐近曲线,其中两个投影平面相图如图2。自由分量最终要衰减为零,故有时又称暂态响应,受迫解有时又称稳态响应
2) 令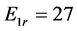 ,
, ,
,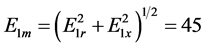 ,
, ,取最后的2%相点作为进入稳态的相图,显然到最后阶段自由分量或称暂态响应已完全消失,剩下的必然是稳态响应。在单谐波源驱动下,受迫解是一个非正弦的周期轨如图3。
,取最后的2%相点作为进入稳态的相图,显然到最后阶段自由分量或称暂态响应已完全消失,剩下的必然是稳态响应。在单谐波源驱动下,受迫解是一个非正弦的周期轨如图3。
3) 令 ,
,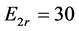 ,
,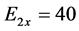 ,
,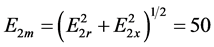 ,
,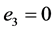 在双谐波源的驱动下,受迫解的相图已出现混沌的性状,但相图还不是十分复杂,轨线并没有充满显示范围如图4。
在双谐波源的驱动下,受迫解的相图已出现混沌的性状,但相图还不是十分复杂,轨线并没有充满显示范围如图4。
4) 令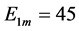 ,
, ,
, ,
, ,
,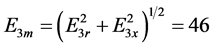 在三谐波源的驱动下,画出的相图,其轨线的充满性和遍历性,已完全具备混沌的性状。其两个投影平面相图如图5,直观而言已很明显是一个混沌函数了,由此说明多谐波在非线性电路的混频会产生混沌。本文图题的符号采用
在三谐波源的驱动下,画出的相图,其轨线的充满性和遍历性,已完全具备混沌的性状。其两个投影平面相图如图5,直观而言已很明显是一个混沌函数了,由此说明多谐波在非线性电路的混频会产生混沌。本文图题的符号采用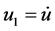 ,
,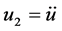 。
。

Figure 1. Example 1 circuit
图1. 例1电路
 (a)
(a) (b)
(b)
Figure 2. Set
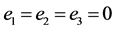 (a)
(a) ; (b)
; (b)

图2. 设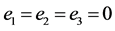 (a) 画
(a) 画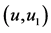 ;(b) 画
;(b) 画
 (a)
(a) (b)
(b)
Figure 3. Set (a)
(a) ; (b)
; (b)

图3. 设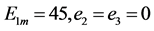 (a) 画
(a) 画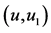 ;(b) 画
;(b) 画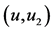
 (a)
(a) (b)
(b)
Figure 4. Set
 (a)
(a) ; (b)
; (b)
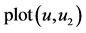
图4. 设 (a) 画
(a) 画 ;(b) 画
;(b) 画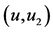
 (a)
(a) (b)
(b)
Figure 5. Set
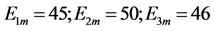 (a)
(a) ; (b)
; (b)

图5. 设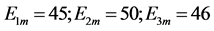 (a) 画
(a) 画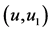 ;(b) 画
;(b) 画
3. 用仿真相图求证受迫振荡的混沌态
此处所指混沌态是指,在仿真Ts时间内画出的相图是非周期的。如果在Ts时间内画出的相图只有起始线头,没有终止线头,说明轨线经过一定暂态过程后最后形成闭轨,或者去除初始的暂态部份,留下最后的稳态部份是一个闭轨,说明是一个周期振荡。如果在仿真时间内画出的相图,仍出现终止线头,说明在Ts时间内尚未形成闭轨是非周期的。由于在Ts时间内画出的相图,遍历性的充满整个相平面,从直观而言,无法发现是否有终止线头,也就无法分清轨线最后是否闭合。
因而,当代求证混沌相图的非周期性,有一种方法是用李亚普诺夫指数,这种方法是相图画出后,无法直观判出其周期性。再用李指数运算程序重新运行一遍,求证相邻两条轨线分离性的数值统计平均值。这种方法的求证结果,仍然和李亚普诺夫指数运算程序的运行时间有关,不同运行时间有不同结果。
如果我们是在作图的过程中,分段观察轨线的描写过程,就可以发现在仿真时间Ts的最后阶段,轨线是否重复进入前面的轨道。设作图语句先画出0.90 Ts - 0.95 Ts的相图A,如果在这个相图内没有终止线头,说明轨线已进入重复性轨道,再画出0.90 Ts - Ts的相图B,必然有A与B相同吻合。如果相图B与A的轨线并不相同,而是轨线增多比相图A更加稠密,更加密集的遍布整个相平面,说明在0.95 Ts - Ts的间隔内,轨线没有重复性的进入前面的轨道,轨线还在继续延长。则相图在Ts时间内是非周期的。
本文的图6至图8,画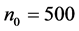 万点,记
万点,记 ,
,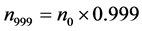 ,用
,用 表示取最后的998‰至999‰相点画相图(a)。用
表示取最后的998‰至999‰相点画相图(a)。用 表示取最后的998‰至1000‰相点画相图(b)。比较两图可以发现,图(b)的轨线比图(a)更加稠密,说明画到500万点的最后阶段,在时间Ts内没有完成一个周期是混沌的。
表示取最后的998‰至1000‰相点画相图(b)。比较两图可以发现,图(b)的轨线比图(a)更加稠密,说明画到500万点的最后阶段,在时间Ts内没有完成一个周期是混沌的。
4. 主谐波解的混沌态与周期态
4.1. 主谐波解是一个周期函数
画一个相图,在较短Ts时间内是非周期的,延长仿真时间Ts可能是周期的。为了说明相图的周期性与仿真时间Ts密切相关。我们近似的求出它的主体基本部份主谐波解[7] -[10] 。
Mathematica用两个程序求出例1的主谐波解如式(7),这是一个包含三个谐波的周期函数。三个激励频率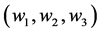 如式(6d)。第一个程序Main
harA.nb采用谐波平衡原理求解,程序运算中忽略非主谐波的影响。第二个程序Power balance.nb采用功率平衡原理求解,此程序用相量法列出三个主谐波成份的KCL与KVL,不是各自求出三个主谐波而后迭加,三个成份是非线性耦合相互关联的,因而三个复数方程要联合求解。两个程序求解结果是一致的如式(7)。两种方法相互印证求解结果的正确性。
如式(6d)。第一个程序Main
harA.nb采用谐波平衡原理求解,程序运算中忽略非主谐波的影响。第二个程序Power balance.nb采用功率平衡原理求解,此程序用相量法列出三个主谐波成份的KCL与KVL,不是各自求出三个主谐波而后迭加,三个成份是非线性耦合相互关联的,因而三个复数方程要联合求解。两个程序求解结果是一致的如式(7)。两种方法相互印证求解结果的正确性。
 (7)
(7)
 (a)
(a) (b)
(b)
Figure 6. (a)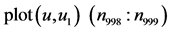 ; (b)
; (b)
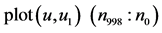
图6. (a) 画 从998‰至999‰;(b) 画
从998‰至999‰;(b) 画 从998‰至1000‰
从998‰至1000‰
 (a)
(a) (b)
(b)
Figure 7. (a) ; (b)
; (b)
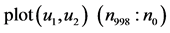
图7. (a) 画 从998‰至999‰;(b) 画
从998‰至999‰;(b) 画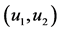 从998‰至1000‰
从998‰至1000‰
 (a)
(a) (b)
(b)
Figure 8. (a) ; (b)
; (b)
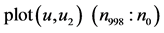
图8. (a) 画 从998‰至999‰;(b) 画
从998‰至999‰;(b) 画 从998‰至1000‰
从998‰至1000‰
本文的图9至图12用Mathematica程序的作图语句画相图。程序Long-cycle.nb显示, 的最大公约数即主谐波解的基频
的最大公约数即主谐波解的基频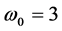 弧/秒,或
弧/秒,或 ,用微妙
,用微妙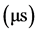 做为计算单位,则周期
做为计算单位,则周期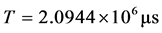 ,由于周期太长,如果画一周期的相图,其轨线遍布充满整个显示范围,染成一片黑色。如图9只画出一周期的五千份之一,轨线的密集性,遍布性,充满性已无法看清轨线有否初始和终止线头。
,由于周期太长,如果画一周期的相图,其轨线遍布充满整个显示范围,染成一片黑色。如图9只画出一周期的五千份之一,轨线的密集性,遍布性,充满性已无法看清轨线有否初始和终止线头。
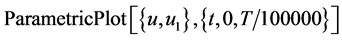 (8)
(8)
 (9)
(9)

Figure 9. Phase portrait of the T/5000
图9. 五千份之一周期的相图
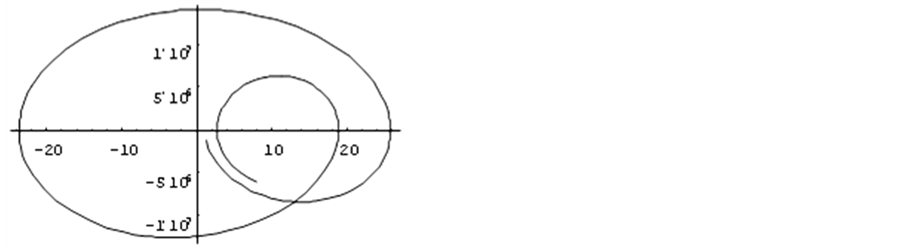
Figure 10. Phase portrait of the T/100,000
图10. 10万份之一周期的相图
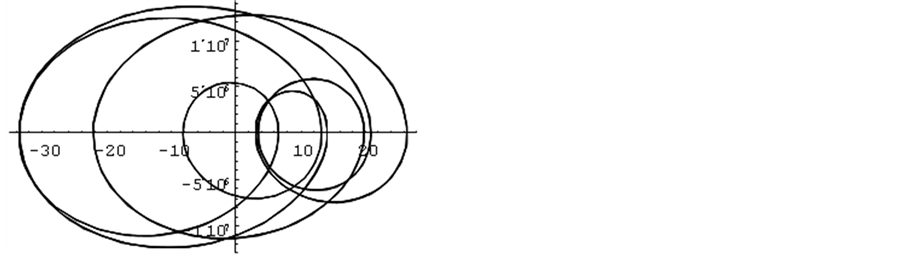
Figure 11.
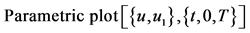
图11. 画一周期的相图

Figure 12.

图12. 画95%周期的相图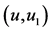
程序Long-cycle.nb用参数式的作图语句画相图,如果将仿真时间Ts缩短到十万份之一,就能看到相图的轨线有起始与终止线头,为了求证式(7)的周期,程序Long-cycle.nb用式(8)和(9)两个作图语句,画出两个完全相同的相图如图10,第一作图语句式(8),作图的起始点 μs,终止点
μs,终止点 μs。第二作图语句式(9),作图的起始点
μs。第二作图语句式(9),作图的起始点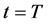 μs,终止点
μs,终止点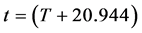 μs,两作图语句轨线均仅仅包含一周期的十万份之一。程序显示的两个相图完全吻合一致,证明周期函数式(7)的周期是
μs,两作图语句轨线均仅仅包含一周期的十万份之一。程序显示的两个相图完全吻合一致,证明周期函数式(7)的周期是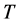 ,图10只画出一周期十万份之一的轨线,可发现图中有很明显的初始和终止线头。
,图10只画出一周期十万份之一的轨线,可发现图中有很明显的初始和终止线头。
以上说明,尽管式(7)是一个周期函数,但如果仿真时间Ts较长,轨线最终是否闭合是看不清的,例如图9。在这种情况下,一个完整周期的相图黑蓝色涂满整个显示范围,其性状是看不清的。如果仿真时间较短例如图10,在仿真时间内可明显的看出有初始和终止线头是非周期的。式(7)是主谐波平衡方程的解,显然是周期的,但如果作图语句的时间间隔取 ,则可显示为非周期的。
,则可显示为非周期的。
4.2. 取公共基频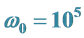 弧/秒求主谐波解的周期态
弧/秒求主谐波解的周期态
如果我们构造一个周期较短的周期函数,则可在Mathematica程序作图时间内画出一个完整周期的相图。譬如例1取三个激励角频率都是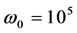 的整数倍; 用程序Main harB.nb求主谐波解如式(10),它的公共基频
的整数倍; 用程序Main harB.nb求主谐波解如式(10),它的公共基频 ,周期
,周期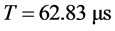 。式中含基波
。式中含基波 ,三次谐波
,三次谐波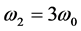 ,六次谐波
,六次谐波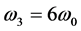 是一个周期函数。
是一个周期函数。
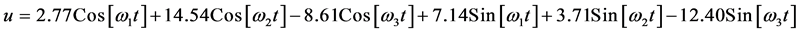 (10a)
(10a)
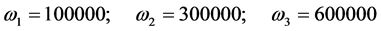 (10b)
(10b)
程序Short-cycle.nb用作图语句画两个相图,图11画一个完整周期的相图,可以看清是一个多循环的闭合周期轨,含三个正弦波的合成;图12画95%周期的相图,明显发现有起始线头和终止线头。
4.3. 取公共基频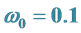 弧/秒求主谐波解的周期态
弧/秒求主谐波解的周期态
如果我们构造一个周期更长的周期函数,当例1取三个激励角频率都是 的整数倍时;用程序Main harC.nb求主谐波解如式(11),与式(7)比较可发现,除了三个主谐波频率增加小数点后的尾数,此外,式(11)与式(7)是完全相同地。
的整数倍时;用程序Main harC.nb求主谐波解如式(11),与式(7)比较可发现,除了三个主谐波频率增加小数点后的尾数,此外,式(11)与式(7)是完全相同地。
 (11a)
(11a)
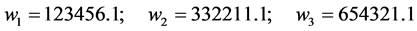 (11b)
(11b)
式(11)的公共基频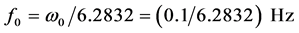 ,周期
,周期 秒。式中没有基波,有三个主谐波
秒。式中没有基波,有三个主谐波 ,
, ,
, 。
。
程序Very-long-cycle.nb用MATH作图语句说明,周期已发生变化。如果周期取6.283秒,用式(8)和(9)两个作图语句,画出的两个相图完全不同,证明在含有尾数的情况下,受迫振荡的周期 。如果周期取
。如果周期取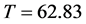 秒,则画出的两个相图完全相同。证明周期已延长到
秒,则画出的两个相图完全相同。证明周期已延长到 秒。以上说明,三个主频率增加小数后的尾数,用MATH作图可发现两者的周期有明显的不同。
秒。以上说明,三个主频率增加小数后的尾数,用MATH作图可发现两者的周期有明显的不同。
5. 公共基频取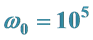 弧/秒,求仿真解的周期态
弧/秒,求仿真解的周期态
如果例1取三个激励频率都是 弧/秒的整数倍如式(10b),用Matlab的Simulink画式(5)的仿真相图,如果作图语句的
弧/秒的整数倍如式(10b),用Matlab的Simulink画式(5)的仿真相图,如果作图语句的 万点,可发现画最后10%相点的相图与画最后1%相点的相图是完全一致的如图13,说明轨线已进入重复的轨道。如图13是其中的两个平面投影,显然是一个周期解,但用Fourier级数分解出的谐波,除了如式(10)的三个主谐波以外,由于三个激励频率在非线性元件混频,还会产生众多的倍频与组合频率成份,因而相图11和图13的形状是不同的。但两图振荡范围的横座标是很近似的。即使将作图语句的
万点,可发现画最后10%相点的相图与画最后1%相点的相图是完全一致的如图13,说明轨线已进入重复的轨道。如图13是其中的两个平面投影,显然是一个周期解,但用Fourier级数分解出的谐波,除了如式(10)的三个主谐波以外,由于三个激励频率在非线性元件混频,还会产生众多的倍频与组合频率成份,因而相图11和图13的形状是不同的。但两图振荡范围的横座标是很近似的。即使将作图语句的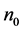 延长增多到500或1000万点,其轨线始终在重复,相图恒保持不变。
延长增多到500或1000万点,其轨线始终在重复,相图恒保持不变。
事实上,用Matlab的Simulink画相图全部是周期解。即使例1取原来三个激励角频率如式(6b)都是3弧/秒的整数倍,这时振荡周期 秒,只要非线性特性高次方项的幂次是整数,则任何角频率成份都是基频的整数倍,画出的相图也是周期解,只不过是因周期太长,我们在仿真时间
秒,只要非线性特性高次方项的幂次是整数,则任何角频率成份都是基频的整数倍,画出的相图也是周期解,只不过是因周期太长,我们在仿真时间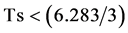 秒内显示为非周期的混沌。即使计算机的内存能允许仿真时间延长到
秒内显示为非周期的混沌。即使计算机的内存能允许仿真时间延长到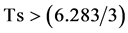 秒,这时的相图应该形成闭轨;但轨线遍历性的充满整个显示范围,最后应该没有终止线头的结果根本看不出来。
秒,这时的相图应该形成闭轨;但轨线遍历性的充满整个显示范围,最后应该没有终止线头的结果根本看不出来。
6. 多谐波混频诞生混沌的普遍性
只要将电路网络的结构与元件参数做适当变化,又可构造出另一混沌方程。
例2:电路如图14,由四条垂直支路的KCL可列式(12a);由中间网孔的KVL可列出式(12b);以(12b)代入(12a),并经整理化简可得式(13),图中各元件的参数如式(14)。此例的很多性质和例1是很类似的。
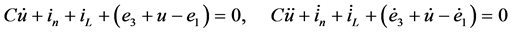 (12a)
(12a)
 (12b)
(12b)
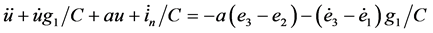 (13a)
(13a)
 (13b)
(13b)
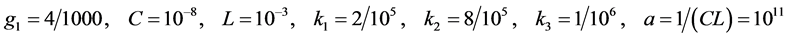 (14a)
(14a)
 (14b)
(14b)
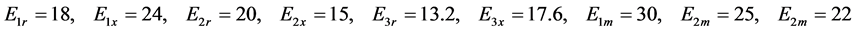 (14c)
(14c)
 (14d)
(14d)
 (a)
(a) (b)
(b)
Figure 13. (a)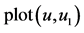 ; (b)
; (b)
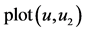
图13. (a) 相图 ;(b) 相图
;(b) 相图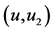

Figure 14. Example 2 circuit
图14. 例2电路
6.1. 谐波成份增多相图性状的演变类似于例1
1) 当 ,在一定起始条件下,式(13)的自由分量,是一条趋于零的渐近曲线,如相图15。
,在一定起始条件下,式(13)的自由分量,是一条趋于零的渐近曲线,如相图15。
2) 当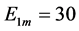 ,
, ,取最后的1%相点做为进入稳态的相图,到最后阶段自由分量已完全消失,剩下的稳态响应。在单谐波源驱动下,受迫解是一个非正弦的周期轨如相图16。
,取最后的1%相点做为进入稳态的相图,到最后阶段自由分量已完全消失,剩下的稳态响应。在单谐波源驱动下,受迫解是一个非正弦的周期轨如相图16。
3) 当 ,
, ,
, 在双谐波源的驱动下,受迫解的相图已出现混沌的性状,如相图17。
在双谐波源的驱动下,受迫解的相图已出现混沌的性状,如相图17。
4) 当 ,
,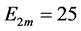 ,
,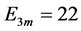 在三谐波源的驱动下,画出的相图,其轨线的充满性和遍历性,已完全具备混沌的性状如图18,直观而言已很明显是一个混沌函数了,由此说明多谐波在非线性电路的混频会产生混沌。图中符号
在三谐波源的驱动下,画出的相图,其轨线的充满性和遍历性,已完全具备混沌的性状如图18,直观而言已很明显是一个混沌函数了,由此说明多谐波在非线性电路的混频会产生混沌。图中符号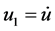 ,
, 。
。

Figure 15. e1 = e2 = e3 = 0 plot (u, u1)
图15. e1 = e2 = e3 = 0画(u, u1)

Figure 16. E1m = 30, e2 = e3 = 0 plot (u, u1)
图16. E1m = 30, e2 = e3 = 0画(u, u1)

Figure 17. E1m = 30, E2m = 25, e3 = 0 plot (u, u1)
图17. E1m = 30, E2m = 25, e3 = 0画(u, u1)

Figure 18. E1m = 30, E2m = 25, E3m = 22, plot (u, u1)
图18. E1m = 30, E2m = 25, E3m = 22, 画(u, u1)
程序Example-21/22/23. nb求式(13)三种情况下的主谐波解如式(15),其最大值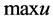 和仿真相图横座标的最大值是相当接近的。
和仿真相图横座标的最大值是相当接近的。
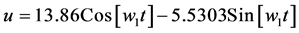 (15a)
(15a)
 (15b)
(15b)
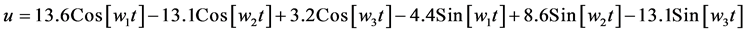 (15c)
(15c)
对应于单谐波源驱动的情况,用程序Example-21.nb求出式(15a)是图16的基波解,其中要注意,偶次方项的展开对基波没有贡献[11] [12] 。对应于两个谐波源驱动的情况,用程序Example-22.nb求出式(15b)是图17的主谐波解,对应于三个谐波源驱动的情况,用程序Example-23.nb求出式(15c)是图18的三个主谐波解。
6.2. 用仿真相图求证受迫振荡的混沌态
在三个谐波源驱动下,图19画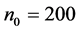 万点,记
万点,记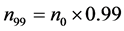 ,
,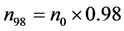 ,用
,用 表示取最后的98%至99%相点画相图19(a)。用
表示取最后的98%至99%相点画相图19(a)。用 表示取最后的98%至100%相点画相图19(b)。比较两图可以发现,图19(b)的轨线比图19(a)更加稠密,说明画到200万点的最后阶段并没有完成一个周期,是混沌的。事实上,图19(a)的轨线加上图18的轨线(最后的99%至100%相点画出的)就是相图19(b)。
表示取最后的98%至100%相点画相图19(b)。比较两图可以发现,图19(b)的轨线比图19(a)更加稠密,说明画到200万点的最后阶段并没有完成一个周期,是混沌的。事实上,图19(a)的轨线加上图18的轨线(最后的99%至100%相点画出的)就是相图19(b)。
6.3. 公共基频取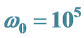 弧/秒,求仿真解的周期态
弧/秒,求仿真解的周期态
如果例2取三个激励频率都是 弧/秒的整数倍如式(10b),周期
弧/秒的整数倍如式(10b),周期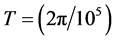 秒
秒 。用Matlab的Simulink画式(13)的仿真相图,其振荡周期大大缩短,如果作图语句的
。用Matlab的Simulink画式(13)的仿真相图,其振荡周期大大缩短,如果作图语句的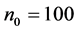 万点,可以发现画最后90%至95%的相点与画最后90%至100%的相点,两个相图是完全一致的如图20,说明轨线已进入重复的轨道。图20是其中的两个平面投影,显然是一个多循环的周期解。
万点,可以发现画最后90%至95%的相点与画最后90%至100%的相点,两个相图是完全一致的如图20,说明轨线已进入重复的轨道。图20是其中的两个平面投影,显然是一个多循环的周期解。
 (a)
(a) (b)
(b)
Figure 19. (a) ; (b)
; (b)
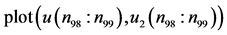
图19. (a) 画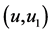 从98%至99%;(b) 画
从98%至99%;(b) 画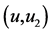 从98%至100%
从98%至100%
 (a)
(a) (b)
(b)
Figure 20. (a) ; (b)
; (b)
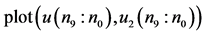
图20. (a) 画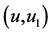 从90%至100%;(b) 画
从90%至100%;(b) 画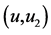 从90%至100%
从90%至100%
7. 结论
1) 混沌是非线性微分方程的图形解,它的一切属性取决于微分方程本身的属性(例如微分方程是确定性的,则混沌相图也是唯一确定的)。任何超越或违背微分方程基本理论的任何解释都是错误的,如果这其间出现矛盾,问题一定是出在数值仿真的算法,特别是算法的精度。混沌的解析表达式在任何数学手册里找不到,根本写不出来。如果写得出其表达式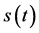 ,用
,用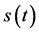 代入原方程,它必须满足方程的平衡。因而对混沌图形(相图)的定性分析,要紧紧依靠它和微分方程的相关性。例如著名的Lorenz方程,其偶次方的非线性项,和双翅膀蝴蝶型的相图相联系;典型的蔡氏电路,其奇次方的非线性项和双涡卷型的相图相联系。多翅膀和多涡卷的相图,不管多到什么复杂程度,它也是一条庞大的空间曲线,如果能写出它的参数式,代入原方程也必须满足方程的平衡(否则它就不是方程的解)
[13] [14] 。研究混沌相图的性状,一定和只能从画出相图的微分方程着手,这其中最困难的是,相图的性状不但与方程的表达式有关,且与式中的常数密切相关,其中的相关规律无法解析的分析出来。
代入原方程,它必须满足方程的平衡。因而对混沌图形(相图)的定性分析,要紧紧依靠它和微分方程的相关性。例如著名的Lorenz方程,其偶次方的非线性项,和双翅膀蝴蝶型的相图相联系;典型的蔡氏电路,其奇次方的非线性项和双涡卷型的相图相联系。多翅膀和多涡卷的相图,不管多到什么复杂程度,它也是一条庞大的空间曲线,如果能写出它的参数式,代入原方程也必须满足方程的平衡(否则它就不是方程的解)
[13] [14] 。研究混沌相图的性状,一定和只能从画出相图的微分方程着手,这其中最困难的是,相图的性状不但与方程的表达式有关,且与式中的常数密切相关,其中的相关规律无法解析的分析出来。
2) 本文用频域的分析方法得出有价值的重要结论。我们比较两种情况,第一种,如果三个激励频率取式(6d),则式(5)的的基频是3弧/秒,周期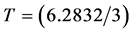 秒。如果考虑
秒。如果考虑 ,求含有非主谐波的仿真解就可得出解的混沌态如例1的图6至图8,例2的图19。
,求含有非主谐波的仿真解就可得出解的混沌态如例1的图6至图8,例2的图19。
第二种,如果三个激励频率取式(10b),则例1或例2的周期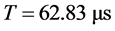 ,包含非主谐波在内的仿真解包含更多的谐波,非线性方程的周期解显示为如例1的图13和例2的图20。
,包含非主谐波在内的仿真解包含更多的谐波,非线性方程的周期解显示为如例1的图13和例2的图20。
两种情况很有力的说明,非线性微分方程的表达式完全一样,比较式(6d)和式(10b)可以发现,三个激励频率的差别也没有超过一个数量级。但方程解的性状发生质的根本性变化。近代非线性科学的迅猛发展说明,非线性方程解的性状和方程中参数的微小变化密切相关。归根结底只有周期的长短之分。要区分周期与非周期必须首先定义仿真时间。
3) 本文提出的两个例证说明,频率不同的多个激励源的混频会诞生混沌,电路图结构与电路元件参数多种多样的变化,可以构造出多种多样的混沌方程。此类电路的特点是有一个非线性正性电阻,没有自激振荡。网络中包含有适当的储能元件,由此组成的二阶动态电路网络,普遍能诞生混沌。这类电路有广泛的实用价值。
无损耗电路诞生混沌要构造非线性电感,蔡氏电路构造负性电导要用有源器件,混频电路只要有一个普通的正性非线性电阻就可以了,其他的都是通常的线性器件,并且对非线性特性没有苛刻的要求,本文两个例证的非线性特性是不同的。实际的非线性电阻,高次方项可能是非整数幂次,则混频后展开为谐波,包含有倍频与组合频率成份,其公共基频可能小于3弧度/秒,则周期会延长到大于(6.2832/3)秒,在一定仿真时间内,更可以诞生混沌。由此要构造一个混沌信号发生器是普遍可行的。
4) 对于已求出主谐波解的式(7)与(10),本文用Mathematica程序的作图语句画相图9至图12。对于其他的动态方程,用Matlab的Simulink画相图。
基金项目
国家自然科学基金资助项目(No. 60662001)。
参考文献 (References)
- [1] Huang, B.H., Wei, Y.F. and Huang, Y. (2014) Describing chaos of continuous time system using bounded space curve. Journal of Modern Physics, 5, 1489-1501.
- [2] 黄炳华, 刘慧杰, 梁永清 (2014) 一阶微分电路构成的混沌. 现代物理, 4, 86-99.
- [3] Huang, B.H., Li, G.M. and Liu, H.J. (2014) Power balance theorem of frequency domain and its application. Journal of Modern Physics, 5, 1097-1108.
- [4] Huang, B.H. and He, X.Y. (2014) Power balance of multi-harmonic components in nonlinear network. Journal of Modern Physics, 5, 1321-1331.
- [5] 黄炳华, 李广明, 卫雅芬 (2012) 用虚功平衡原理求解无损耗系统的主谐波. 现代物理, 2, 60-69.
- [6] 黄炳华, 李广明, 刘慧杰 (2013) 由无损耗电路构成的非周期振荡. 现代物理, 1, 1-8.
- [7] 冯久超, 李广明 (2012) 功率平衡理论在研究非线性电路与混沌中的进展. 华南理工大学学报, 11, 13-18.
- [8] 梁永清, 黄炳华 (2014) 非线性电路频域的功率平衡. 太原理工大学学报, 3, 328-333.
- [9] Huang, B.H., Huang, X.M. and Li, H. (2011) Main components of harmonic solutions of nonlinear oscillations. Procedia Engineering, 16, 325-332.
- [10] Huang, B.-H., Yang, G.S., Wei, Y.F. and Huang, Y. (2013) Harmonic analysis method based on power balance. Applied Mechanics and Materials, 325-326; Manufacturing Engineering and Process II, 1508-1514
- [11] 黄炳华, 钮利荣, 蔺兰峰, 孙春妹 (2007) 功率平衡基础上的基波分析法. 电子学报, 10, 1994-1998.
- [12] 黄炳华, 黄新民, 韦善革 (2008) 用基波平衡原理分析非线性振荡与混沌. 通信学报, 1, 65-70
- [13] Yu, S.M., Qiu, S.-S. and Lin, Q.H. (2003) New results of study on generating multiple-scroll chaotic attractors. Science in China (Series F), 46, 104-115.
- [14] 王兴元, 王明军 (2007) 超混沌Lorenz系统. 物理学报, 9, 5136-5141.

附 录
Mathematica程序(按文中出现的先后排序) MainharA.nb; Powerbalance.nb; Long-cycle.nb; MainharB.nb; Short-cycle.nb; MainharC.nb; Very-long-cycle.nb; Example-21. nb; Example-22. nb; Example-23. nb.
NOTES
*通讯作者。