Applied Physics
Vol.05 No.12(2015), Article ID:16445,6
pages
10.12677/APP.2015.512022
Diffusion of Fe Atoms on Al Substrate and Effect of Film Growth Conditions on the Magnetic Properties
Qian Feng, Junjie Chen, Liqing Jiang, Shuangjuan Shen, Zhigao Huang
College of Physics and Energy, Fujian Normal University, Fuzhou Fujian
Received: Nov. 9th, 2015; accepted: Nov. 27th, 2015; published: Nov. 30th, 2015
Copyright © 2015 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
A Monte Carlo technique has been developed for simulating the deposition and diffusion of Fe atoms on Al (100) surfaces, and the growth of Fe clusters. The effects of growth conditions on the Fe fractal morphology and the magnetic properties are investigated. The simulated results indicate that with increasing temperature of substrate, the surface morphology evolves from dispersed growth, fractal growth to dense growth, and finally to another dispersed growth. It is also found that the morphology of Fe film greatly affects the magnetic properties, and ramified atomic aggregate with a more compact morphology has a higher Curie temperature.
Keywords:Monte Carlo Simulation, Diffusion of Fe Atoms, Magnetic Properties

Fe原子在Al基底上的扩散及薄膜生长条件对磁特性的影响
冯倩,陈俊杰,蒋丽钦,沈双娟,黄志高
福建师范大学物理与能源学院,福建 福州

收稿日期:2015年11月9日;录用日期:2015年11月27日;发布日期:2015年11月30日

摘 要
利用蒙特卡罗方法模拟Fe原子在Al基底上的沉积、扩散,以及Fe的团簇形貌的生长演化。研究了薄膜生长条件对Fe薄膜的分形形貌及磁特性的影响。模拟结果表明,随着温度的升高,Fe微观形貌经历了一个从分散成长、分形成长到凝聚成长的变化过程;而Fe薄膜的形貌极大地影响薄膜的磁特性,具有更紧凑的分形形貌的Fe薄膜具有更高的居里温度。
关键词 :蒙特卡罗模拟,Fe原子扩散,磁特性

1. 引言
微结构材料和器件在原子尺寸度上的精确加工是当前材料科学研究发展的重要方向。近几年来,随着实验手段的提高,特别是扫描隧道显微镜和原子力显微镜等用于观察薄膜的生长形貌,人们在研究薄膜生长方面实验上已经取得了许多进展。实验研究表明, 薄膜的生长过程会直接影响薄膜的质量,单原子和原子团簇可以在基板上随机分散和聚合,并形成具有分形结构的微观形貌[1] 。最近,很多学者在实验上研究了Fe薄膜在各种基板上的生长,这种系统由于其低维磁特性及超导特性引起人们的极大兴趣 [2] [3] 。其中,Fe/Al合金薄膜由于其软磁特性和很好的机械特性而备受关注,成为人们广泛应用的磁记录材料 [2] 。铁作为典型的3d电子磁性系统,能够形成很明显的局域磁矩;考虑到α-铁的电子自旋间强相关,人们利用第一性原理计算了各种不同结构的铁材料的磁相互作用 [3] [4] 。不同的薄膜生长条件对其微观形貌影响很大,研究不同微观结构的铁薄膜的磁特性变化是很有意义的课题。
然而,薄膜的生长是非常复杂的过程,凭借实验不能完全跟踪薄膜的生长过程;利用蒙特卡罗算法模拟薄膜的生长过程是研究其生长机理的有效途径 [5] [6] 。Bruschi等人 [5] 提出了原子的沉积、扩散和脱附三个过程的模型,吸附粒子在各个方向运动时要克服的位能是利用Voter理论计算的。P. Zhang [6] 等人在计算原子迁移的跃迁势垒时,利用二体Morse势,采用了将跃迁路径进行合理细分的方法寻求跃迁路径上的最大势能点。如何建立合适模型,模拟磁性薄膜的生长机制,从而掌握磁性纳米结构的形成和稳定性规律等,这将具有十分重要的科学意义。
本工作利用蒙特卡罗方法从原子尺度水平研究Fe/Al薄膜生长机制,模拟Fe原子在Al表面上的沉积、吸附、扩散、成核、生长等一系列复杂过程;并重点研究薄膜的生长条件对Fe/Al薄膜的磁化强度、磁化率及磁相变温度的影响。计算模拟结果将对如何实验上对生长条件进行控制,及薄膜微观形貌对磁性质的影响等起到指导作用。
2. 模型与计算原理
在本文的模拟计算中,考虑到基底表面束缚能、最近邻粒子间耦合能以及应力场对粒子扩散势垒的修正,采用动态蒙特卡罗方法模拟Fe原子在Al(100)基底上的沉积、扩散及团簇生长。首先,考虑Fe原子的覆盖率x为0.1 ml,随机且不重叠地沉积Fe原子在Al基底(80 × 80)正方点阵上。在每一个动态蒙特卡罗步骤里,随机选取一个Fe原子,若该Fe原子的最近邻粒子数为四个,即处于团簇的中间,则该F原子所在团簇在(±X, ±Y)四个方向中任选一个方向作扩散运动;若Fe原子的最近邻粒子数小于四个,即为单一原子团簇或处于团簇的边缘,则该Fe原子在其最近邻空位中随机选择一个作扩散运动,扩散概率的计算如下 [7] :
 (1)
(1)
其中,n为近邻粒子数,T为温度,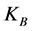 为玻尔兹曼常数,Fe原子在Al(100)基底上的束缚能Es = 0.89 eV [8] ,Fe原子的最近邻原子束缚能Eb = 0.38 eV [9] ,EC则是由于吸附粒子引入的应力场,采用了简单的线性近似,即
为玻尔兹曼常数,Fe原子在Al(100)基底上的束缚能Es = 0.89 eV [8] ,Fe原子的最近邻原子束缚能Eb = 0.38 eV [9] ,EC则是由于吸附粒子引入的应力场,采用了简单的线性近似,即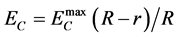 ,其中R为团簇半径,r为粒子到团簇的最小距离,
,其中R为团簇半径,r为粒子到团簇的最小距离, 的最大值
的最大值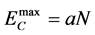 ,N是团簇所含的粒子数,α是常数,定为0.0001,ν为势阱中粒子的振动频率,取为1013 S−1 [7] 。我们通过4000万动态蒙特卡罗步,动态模拟薄膜的生长过程,最后可得到Fe原子在Al基底上生长的微观形貌。
,N是团簇所含的粒子数,α是常数,定为0.0001,ν为势阱中粒子的振动频率,取为1013 S−1 [7] 。我们通过4000万动态蒙特卡罗步,动态模拟薄膜的生长过程,最后可得到Fe原子在Al基底上生长的微观形貌。
为了计算Fe薄膜的磁特性,采用标准蒙特卡罗的Metropolis准则对系统进行模拟 [10] 。利用Heisenberg
模型可将系统的哈密顿量表示为: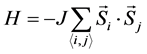 ,
, 是第i个原子自旋取向,
是第i个原子自旋取向, ,
, 是对最近
是对最近
邻原子对的交换相互作用的求和,最近邻铁原子自旋交换相互作用常数J = 1.21 mRy [4] 。本文中,我们抛弃前20,000蒙特卡罗步,而对后面的30,000蒙特卡罗步求平均,在统计计算中,我们每隔10蒙特卡罗步计算一次模拟参数,这样可避免两个连续组态之间的相关性。通过Markov过程产生的自旋组态分布
P(xl)趋于平衡分布: 。则物理量的热平均
。则物理量的热平均 。
。
我们感兴趣的参量有磁化强度,比热,磁化率,利用MC模拟求其统计平均值:
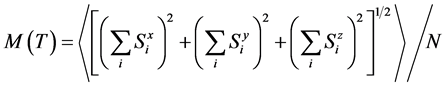 (2)
(2)
 (3)
(3)
T是薄膜的实际温度,E是系统的总能量,M是系统的总磁化强度。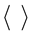 是对利用Markov过程产生的遵循平衡分布的各组态的统计平均。
是对利用Markov过程产生的遵循平衡分布的各组态的统计平均。
3. 结果与讨论
图1显示的不同基底温度Tsu = (300 K, 325 K, 400 K, 500 K, 610 K和620 K)下Fe原子的生长形貌图。从图1(a)可以看出,在基板温度比较低的的情况下(Tsu = 300 K),粒子分散在整个网格中,并没有形成大的团簇。随着基板温度升高,薄膜表面呈现分形成长,但此时团簇的平均分支的宽度基本保持不变,其值近似为单粒子直径,如图1(b)和图1(c)所示。随着基板温度的继续升高,团簇形貌经历了从分形成长到凝聚成长的变化过程,团簇的分支宽度逐渐增大,团簇形貌由枝叉状分形生长过渡到团状生长,从图1(d)到图1(e),我们可以发现,分形团簇的平均宽度不断增大。而当温度达到840 K或继续升高,薄膜表面形貌又呈现了分散成长的形式,如图1(f)所示。之所以出现以上现象是由于温度较低,粒子较不活跃,即扩散能力太弱以致粒子不凝聚成较大的团簇。而当325 K < Tsu ≤ 400 K时,随着温度增高,更高的粒子热激发能使粒子间更容易相遇,聚集成团簇;与此同时,粒子沿团簇的边缘低速扩散,导致团簇分支的宽带比较小。随着温度的增高,团簇分支宽度逐渐增大(400 K < Tsu ≤ 610 K)。这主要是由于基板温度继续增高的情况下,从公式(1)可以计算出粒子沿团簇边缘扩散的概率逐渐增大,这样就导致了团簇分支宽带的逐渐增大。而当Tsu = 700 K时,粒子由于较高的活跃性而最终无法凝聚成一个团簇,薄膜表面又呈现分散生长。

Figure 1. Surface morphologies obtained at six different substrate temperatures (a) Tsu = 300 K, (b) Tsu = 325 K, (c) Tsu = 400 K, (d) Tsu = 500 K, (e) Tsu = 610 K, (f) Tsu = 620 K
图1. 不同基底温度下的薄膜表面形貌图(a) Tsu = 300 K,(b) Tsu = 325 K,(c) Tsu = 400 K,(d) Tsu = 500 K,(e) Tsu = 610 K,(f) Tsu = 620 K
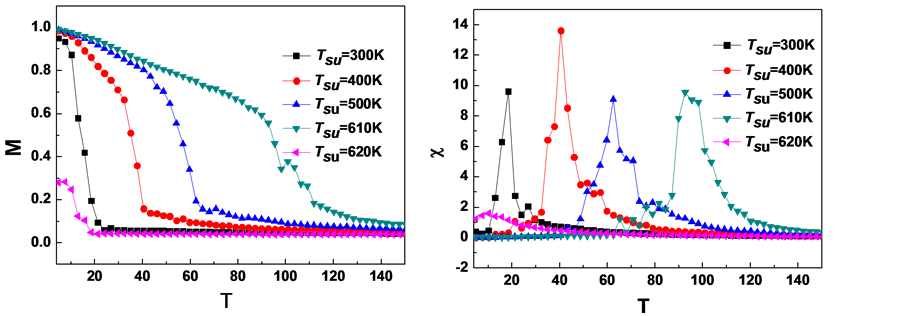
图2给出的是在不同的基板温度生长的薄膜的自发磁化强度、磁化率随薄膜温度的变化。从图3中可以看到,随着薄膜温度的升高,Fe/Al薄膜的自发磁化强度随着系统温度的升高从1降低到了0。具有分形形貌的Fe/Al薄膜((Tsu = 400 K, 500 K, 610 K),对应的Tsu越高,自发磁化强度随着系统温度的升高下降得越慢,意味着这些薄膜具有较高的居里温度。这主要是在因为团簇分支宽度逐渐增大,系统的铁磁相互作用能跟着增大,使铁磁相变温度增大。从图2中还可以看到,对于Fe原子呈分散生长的小团簇时(T = 400 k, 420 k, 720 k),它们在基态的自发磁化强度比较小,且随着温度升高更迅速降低为0。这主要是因为分散生长的薄膜的团簇中所含粒子数都比较少,且可能有许多单个粒子分散在整个基板上,铁磁相互作用能减小,温度升高时热激发能容易破坏粒子有序状态,所以居里温度比较小。图2(b)给出了不同的基板温度下生长的薄膜的磁化率随薄膜温度的变化。当温度趋向于居里温度时,磁化强度迅速减为零,磁化率出现了一个明显的高峰。从磁化率峰可以较准确地确定系统的相变温度。
图3给出了Fe/Al薄膜在Tsu < 430 k时,薄膜表面呈分散成长,居里温度很低。随着基底温度增大,分形团簇开始出现,居里温度也急剧增大。在430 K ≤ Tsu ≤ 530 K温度范围内,居里温度基本保持不变,这是因为在这个温度范围内薄膜分形成长,团簇分支宽度基本不变,形貌也相对比较稳定。当530 K ≤ Tsu ≤ 699 K时,居里温度随着基板温度增大而升高,这是因为此时的团簇分支更加紧凑,分支宽带逐渐增大,原子间的相互作用能也逐渐增大,从而具有更大的相变温度。当基板温度继续增大,相变温度急剧下降,另一种薄膜分散生长开始出现。综上所述,通过改变外界的实验条件(如基底温度等),可以控制Fe原子在Al基板上的扩散速率,从而改变Fe的原子团簇形貌,影响磁性薄膜的自发磁化强度、磁化率以及磁相变温度。
4. 结论
本工作利用动态蒙特卡罗方法模拟Fe原子在Al基底上的沉积、扩散,及Fe的团簇形貌的生长演化,并利用Metropolis准则对Fe/Al薄膜系统进行磁特性研究。结果表明,Fe原子团簇出现非常丰富的分形
 (a)(b)
(a)(b)
Figure 2. Temperature dependence of spontaneous magnetization, magnetic susceptibility of the grown films with different substrate temperatures, Tsu = 300 K, 325 K, 400 K, 500 K, 610 K and 620 K
图2. 在不同的基底温度(Tsu = 300 K, 400 K, 500 K, 610 K及620 K)生长的Fe/Al(100)薄膜的自发磁化强度、磁化率随薄膜温度的变化
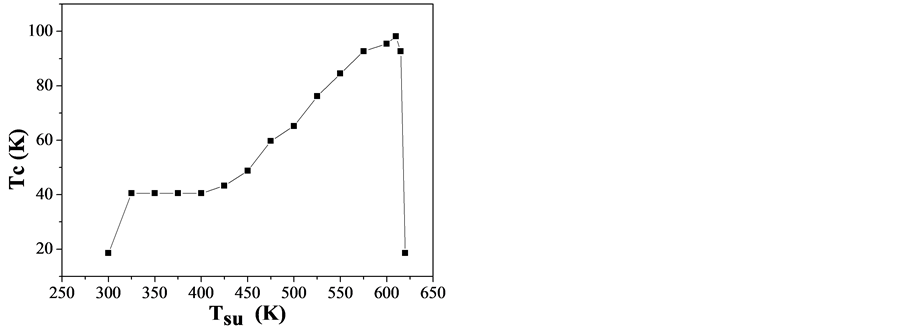
Figure 3. Tc values as a function of Tsu values for Fe/Al film
图3. Fe/Al薄膜的磁相变温度Tc与薄膜生长时的基底温度Tsu的关系曲线
几何特征,当Tsu升高,Fe原子团簇从分散生长、分形生长,到密集的生长,并最终形成另一种分散的生长方式;同时还发现,Fe薄膜的形貌极大地影响薄膜的磁特性,当Fe原子团簇的分枝宽度变大时,或具有更紧凑的分形形貌时,系统具有更高的居里温度。因此,通过改变薄膜的生成条件,可以改变Fe的原子团簇形貌,从而影响磁性薄膜的磁性质。
基金项目
福建省教育厅基金项目(JK2013010, JA13064)。
文章引用
冯倩,陈俊杰,蒋丽钦,沈双娟,黄志高. Fe原子在Al基底上的扩散及薄膜生长条件对磁特性的影响
Diffusion of Fe Atoms on Al Substrate and Effect of Film Growth Conditions on the Magnetic Properties[J]. 应用物理, 2015, 05(12): 159-164. http://dx.doi.org/10.12677/APP.2015.512022
参考文献 (References)
- 1. Avnir, D., Biham, O., Lidar, D., et al. (1998) Is the Geometry of Nature Fractal? Science, 279, 39-40. http://dx.doi.org/10.1126/science.279.5347.39
- 2. Chérifa, S.M., Bouzianea, K., Roussigné, Y., et al. (2007) Growth and Magnetic Study of Sputtered Fe/Al Multilayers. Materials Science and Engineering: B, 138, 16. http://dx.doi.org/10.1016/j.mseb.2006.12.009
- 3. Sandratskii, L.M., Şaşıoğlu, E. and Bruno, P. (2006) Exchange Interactions and Néel Temperature of a Fe Monolayer on W(001): A First-Principles Study. Physical Review B, 73, Article ID: 014430. http://dx.doi.org/10.1103/PhysRevB.73.014430
- 4. Igoshev, P.A., Efremov, A.V. and Katanin, A.A. (2015) Magnetic Exchange in α-Iron from ab Initio Calculations in the Paramagnetic Phase. Physical Review B, 91, Article ID: 195123. http://dx.doi.org/10.1103/PhysRevB.91.195123
- 5. Bruschi, P., Cagnoni, P. and Nannini, A. (1997) Temperature-Dependent Monte Carlo Simulations of Thin Metal Film Growth and Percolation. Physical Review B, 55, 7955. http://dx.doi.org/10.1103/PhysRevB.55.7955
- 6. 张佩峰, 郑小平, 贺德衍, 等. Kinetic Monte Carlo方法对薄膜生长初期表面形貌的研究[J]. 中国科学, 2007(37): 9.
- 7. 许晓军, 王凤飞. 不同温度下团簇生长的Monte Carlo模拟[J]. 计算物理, 2009(26): 758.
- 8. Kim, C. and Chung, Y.C. (2006) Theoretical Calculations on Atomistic Behaviors in Transition Metals (Fe, Co, Ni)-Al Multilayer System: Ab Initio Approach. Applied Surface Science, 252, 8380. http://dx.doi.org/10.1016/j.apsusc.2005.11.044
- 9. Wallenius, J., Olsson, P., Lagerstedt, C., et al. (2004) Modeling of Chromium Precipitation in Fe-Cr Alloys. Physical Review B, 69, 094103. http://dx.doi.org/10.1103/PhysRevB.69.094103
- 10. Jiang, L.Q., Shen, S.J., Zhang, J.M., et al. (2015) Monte Carlo Study on Exchange Bias and Coercivity Properties in Coupled Ferromagnetic/Antiferromagnetic Films. Physica B, 478, 22.